Exponentialfunktion
Definition
Eine Funktion mit der GleichungEigenschaften
Für jede Exponentialfunktion- Der Graph verläuft immer oberhalb der
-Achse, der Wertebereich ist
oder auch
geschrieben.
- Der Graph verläuft immer durch den Punkt
, da
- Für
gilt: Der Graph steigt mit zunehmendem
- Für
gilt: Der Graph fällt mit zunehmendem
- Die
-Achse ist Asymptote:
- Für
gilt: Der Graph nähert sich in negativer
-Richtung der
-Achse.
- Für
gilt: Der Graph nähert sich in positiver
-Richtung der
-Achse.
- Wächst
um den Wert
wird der Funktionswert
mit dem Faktor
multipliziert.
- Der Graph der Funktion
geht aus dem Graphen von
durch Spiegelung an der
-Achse hervor.
Beispiele
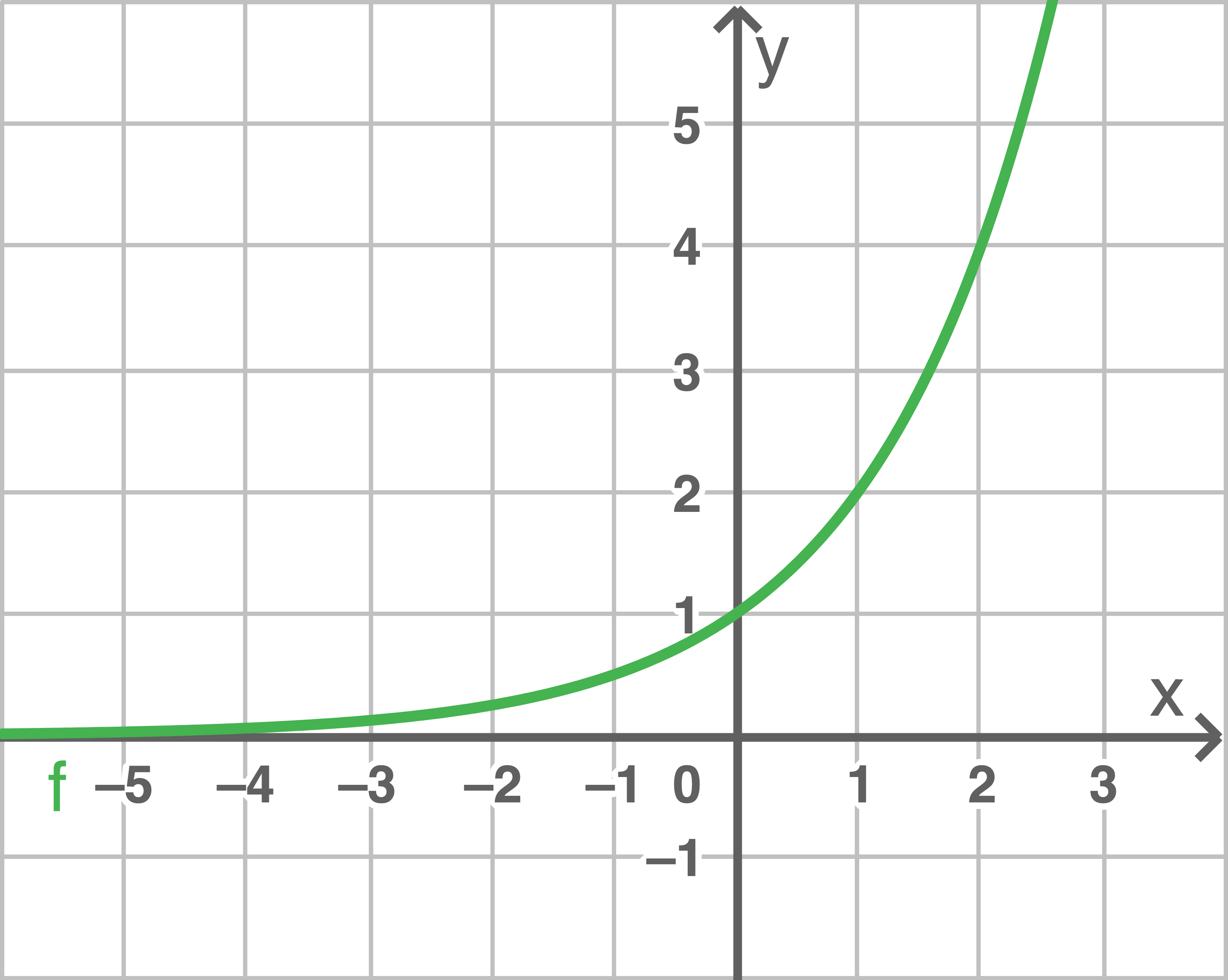
Beispiel für  mit
mit 
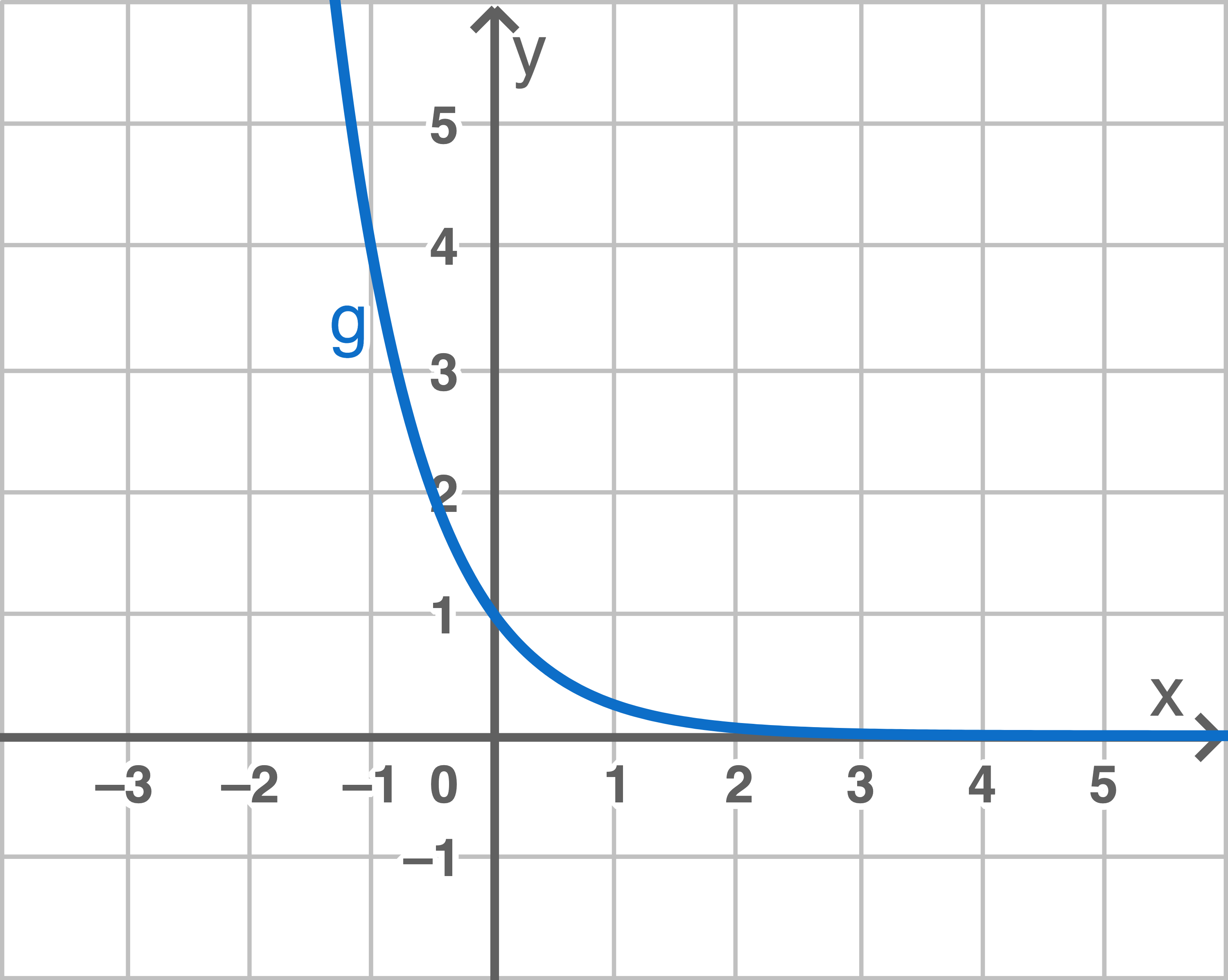
Beispiel für  mit
mit 
1
a)
Zeichne die Graphen zu  und
und  in ein Koordinatensystem.
in ein Koordinatensystem.
b)
Zeige rechnerisch, dass die beiden Graphen durch Spiegelung an der  -Achse auseinander hervorgehen.
-Achse auseinander hervorgehen.
2
Bestimme alle Exponentialfunktionen  mit der jeweiligen Eigenschaft:
mit der jeweiligen Eigenschaft:
a)
Der Graph der Funktion verläuft durch den Punkt 
b)
Der Graph der Funktion verläuft fallend durch den Punkt 
c)
Der Graph der Funktion verläuft fallend durch den Punkt 
d)
Der Graph der Funktion verläuft steigend durch den Punkt 
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
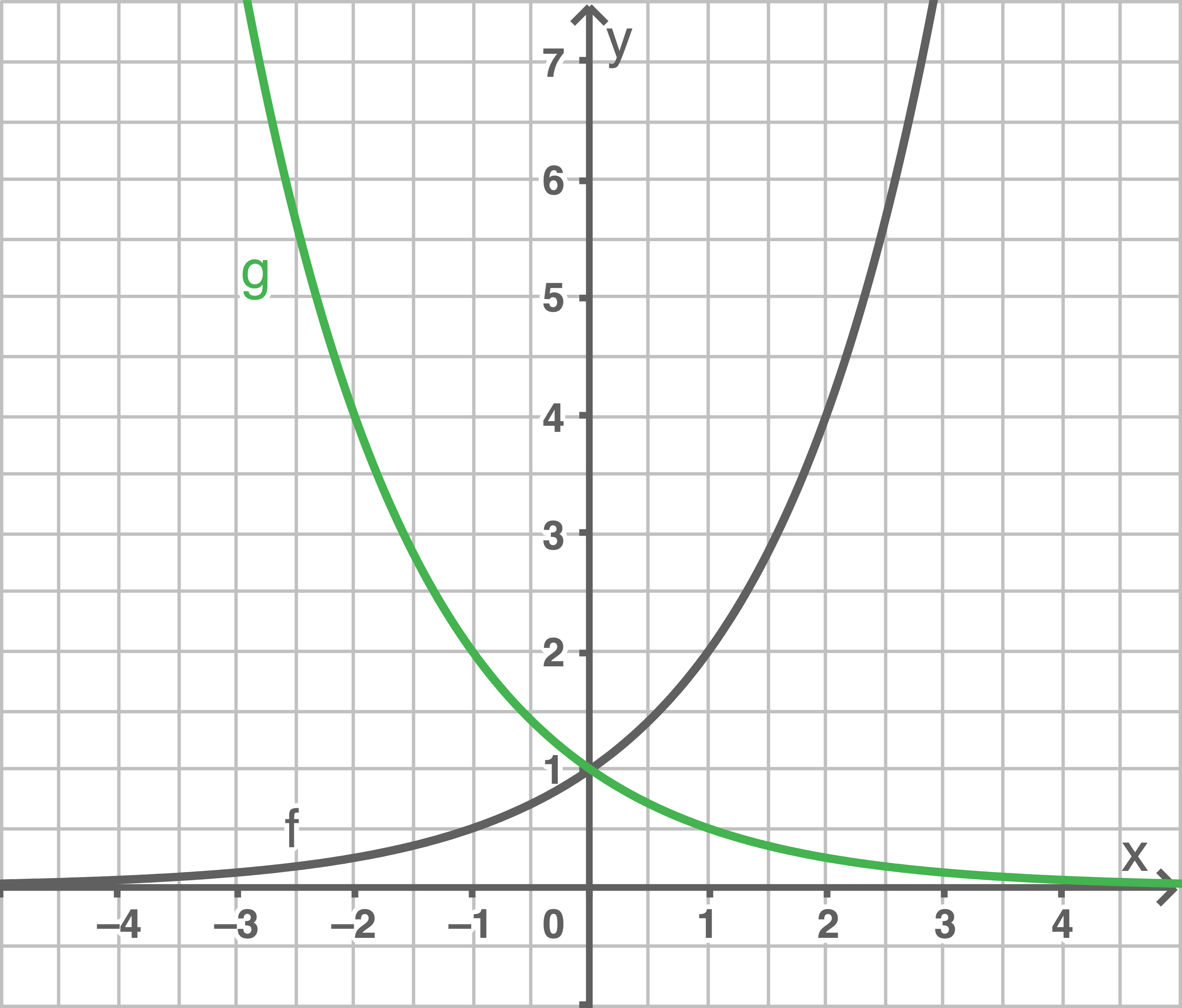
b)
2
a)
b)
b)
d)
Es gibt keine Exponentialfunktion der Form  mit dieser Eigenschaft.
mit dieser Eigenschaft.