Sinussatz
In einem beliebigen Dreieck gilt:

 mit
mit 
 und
und 
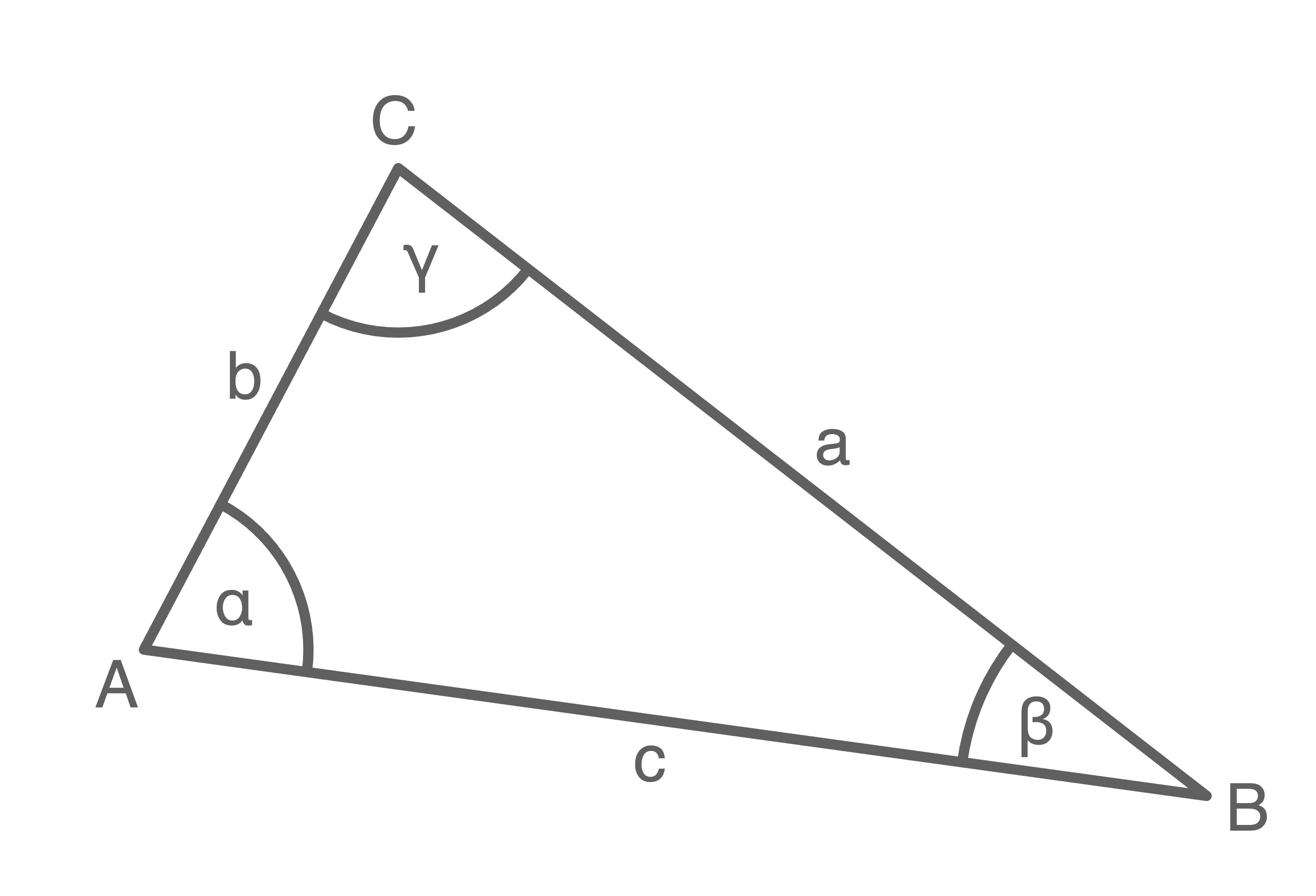 Berechnet werden sollen die Längen der übrigen Strecken des Dreiecks.
Berechnet werden sollen die Längen der übrigen Strecken des Dreiecks.
![\(\begin{array}[t]{rll}
\dfrac{b}{\sin(\beta)}&=&\dfrac{c}{\sin(\gamma)} \quad \scriptsize \mid\;\cdot \sin(\beta) \\[5pt]
b&=&\dfrac{c}{\sin(\gamma)}\cdot \sin(\beta) \\[5pt]
b&=&\dfrac{6,2\,\text{cm}}{\sin(80^\circ)}\cdot \sin(30^\circ) \\[5pt]
b&\approx&3,15\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/507912b9f18dcadd4bacdd3930cb1bce8b9f847a99db69963bfc6228beeb1a6b?color=5a5a5a) Um die Länge der Strecke
Um die Länge der Strecke  zu berechnen, wird die Größe des Winkels
zu berechnen, wird die Größe des Winkels  benötigt:
benötigt:

![\(\begin{array}[t]{rll}
\dfrac{a}{\sin(\alpha)}&=&\dfrac{c}{\sin(\gamma)} \quad \scriptsize \mid\;\cdot \sin(\alpha) \\[5pt]
a&=&\dfrac{c}{\sin(\gamma)}\cdot \sin(\alpha) \\[5pt]
a&=&\dfrac{6,2\,\text{cm}}{\sin(80^\circ)}\cdot \sin(70^\circ) \\[5pt]
a&\approx&5,92\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/82f0cf308696ea00f2c67cdcceccac3c5410f7547a9cd826b8cdd6b86abf7278?color=5a5a5a)
Beispiel
Gegeben ist das Dreieck
1
Berechne die übrigen Längen der Seiten und Größen der Winkel des Dreiecks 


















a)
b)
c)
d)
e)
f)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
d)
e)
f)