Umkehrbarkeit von Funktionen
Wird bei einer Funktion  die Zuordnungsrichtung umgekehrt, so entsteht die umgekehrte Zuordnung. Wenn die umgekehrte Zuordnung eine Funktion ist, so heißt die ursprüngliche Funktion umkehrbar.
Die Umkehrfunktion wird oft mit
die Zuordnungsrichtung umgekehrt, so entsteht die umgekehrte Zuordnung. Wenn die umgekehrte Zuordnung eine Funktion ist, so heißt die ursprüngliche Funktion umkehrbar.
Die Umkehrfunktion wird oft mit  ,
,  oder
oder  bezeichnet.
Wenn
bezeichnet.
Wenn  die Umkehrfunktion von
die Umkehrfunktion von  ist, so entsteht der Graph von
ist, so entsteht der Graph von  durch Spiegelung des Graphen von
durch Spiegelung des Graphen von  an der ersten Winkelhalbierenden.
Ist eine Funktion steigend oder fallend, so ist sie umkehrbar.
Die Funktion
an der ersten Winkelhalbierenden.
Ist eine Funktion steigend oder fallend, so ist sie umkehrbar.
Die Funktion  mit
mit  ist für den Definitionsbereich
ist für den Definitionsbereich  umkehrbar. Die Umkehrfunktion
umkehrbar. Die Umkehrfunktion  hat den Funktionsterm
hat den Funktionsterm 
1
Die jeweilige Abbildung zeigt den Graphen einer Funktion  Entscheide, ob die Funktion umkehrbar ist und begründe.
Entscheide, ob die Funktion umkehrbar ist und begründe.
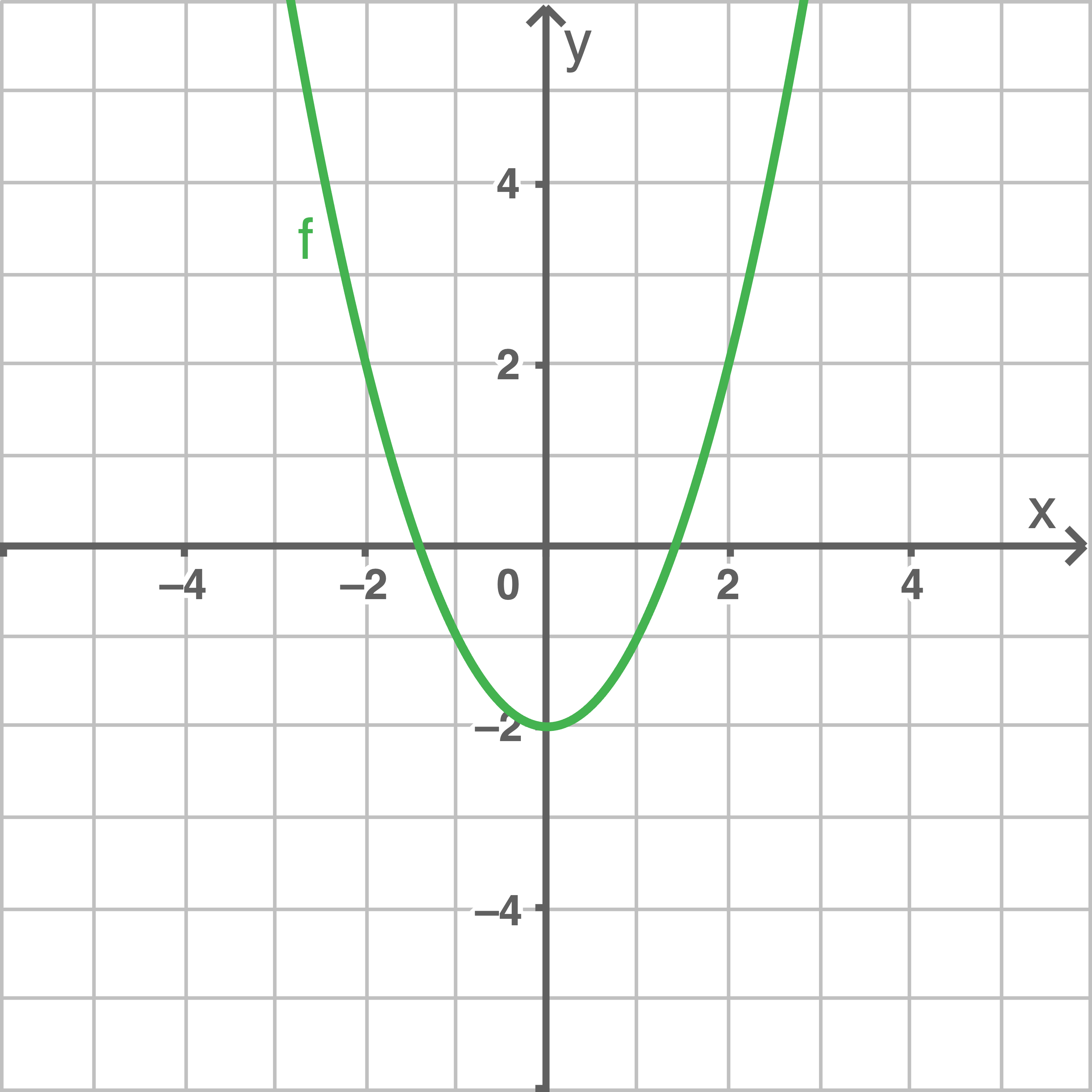
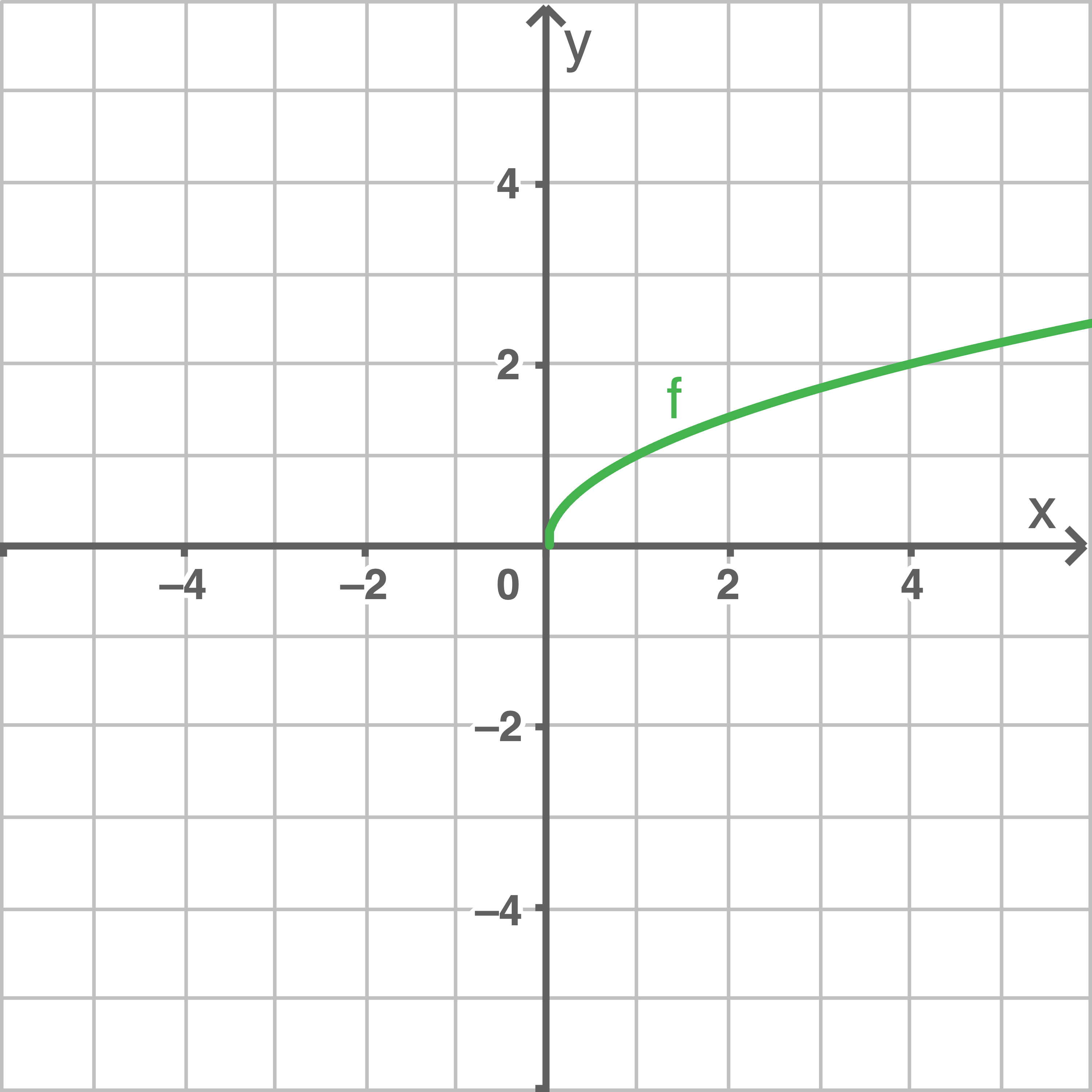
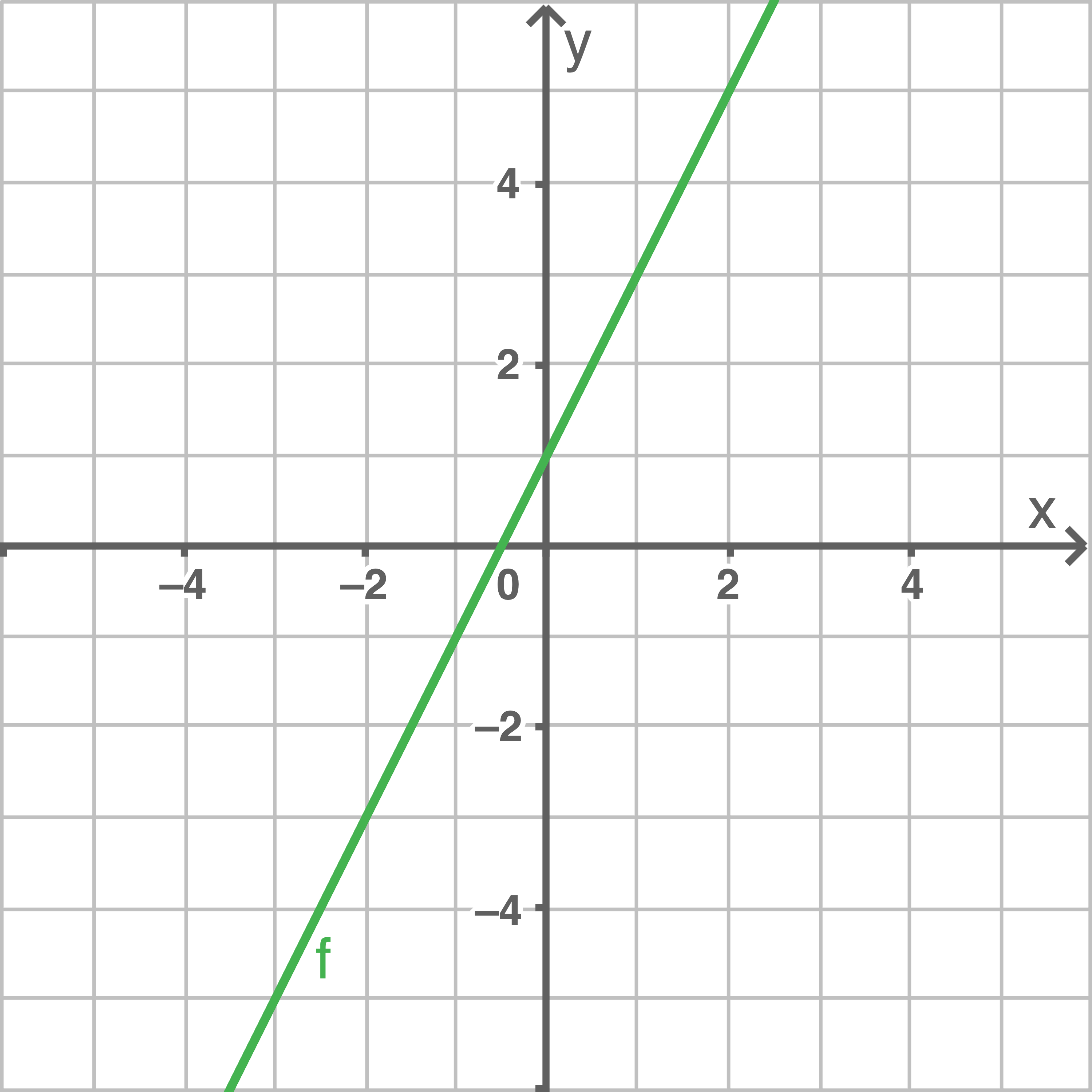
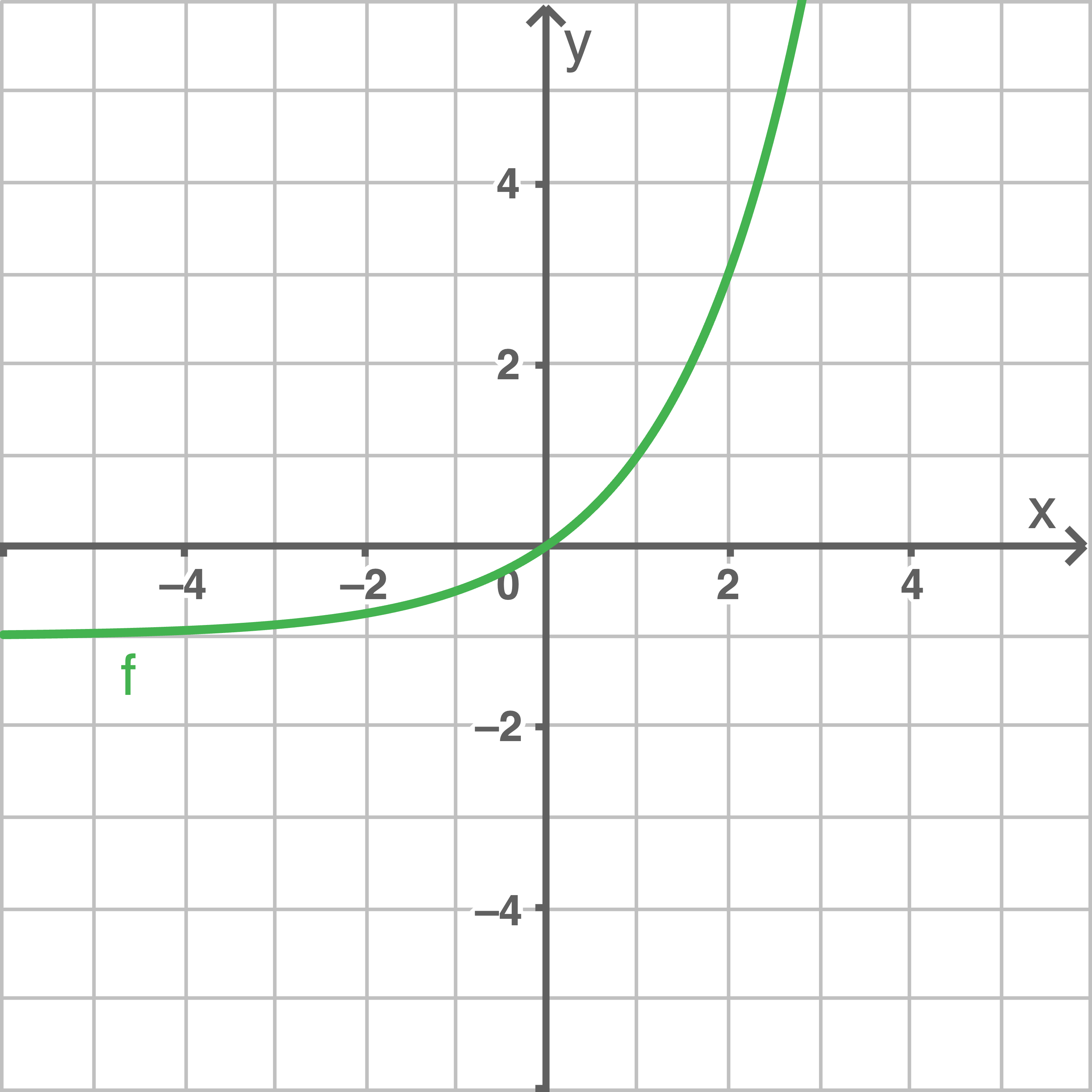
a)

b)

c)

d)

2
Ermittle den Funktionsterm der Umkehrfunktion.




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Die Funktion  ist für
ist für  oder
oder  umkehrbar, nicht jedoch für beide Definitionsbereiche zusammen. Begründung: In dem jeweiligen Intervall fällt oder steigt der Graph der Funktion.
umkehrbar, nicht jedoch für beide Definitionsbereiche zusammen. Begründung: In dem jeweiligen Intervall fällt oder steigt der Graph der Funktion.
b)
Die Funktion  ist umkehrbar, da der Graph der Funktion kontinuierlich steigt.
ist umkehrbar, da der Graph der Funktion kontinuierlich steigt.
c)
Die Funktion  ist umkehrbar, da der Graph der Funktion kontinuierlich steigt.
ist umkehrbar, da der Graph der Funktion kontinuierlich steigt.
d)
Die Funktion  ist umkehrbar, da der Graph der Funktion kontinuierlich steigt.
ist umkehrbar, da der Graph der Funktion kontinuierlich steigt.
2
a)
b)
c)
d)