Verketten von Funktionen
Definition
Die FunktionBeispiel
1
Gib die Gleichung der Funktionen  und
und  mit
mit  und
und  an und zeichne die dazugehörigen Graphen.
an und zeichne die dazugehörigen Graphen.



a)
b)
c)
2
Gib zwei Funktionen  und
und  an, sodass
an, sodass  gilt.
gilt.




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
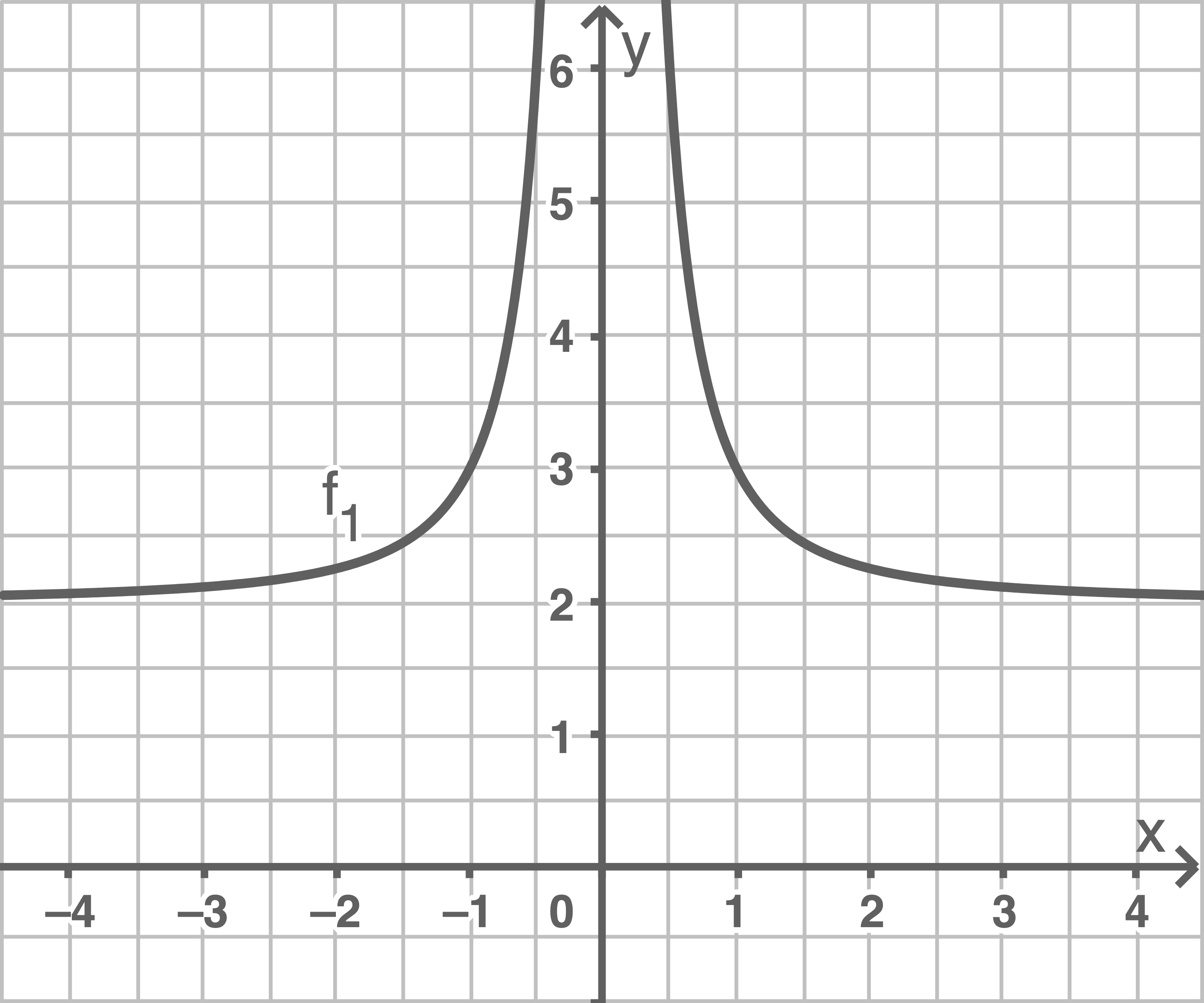
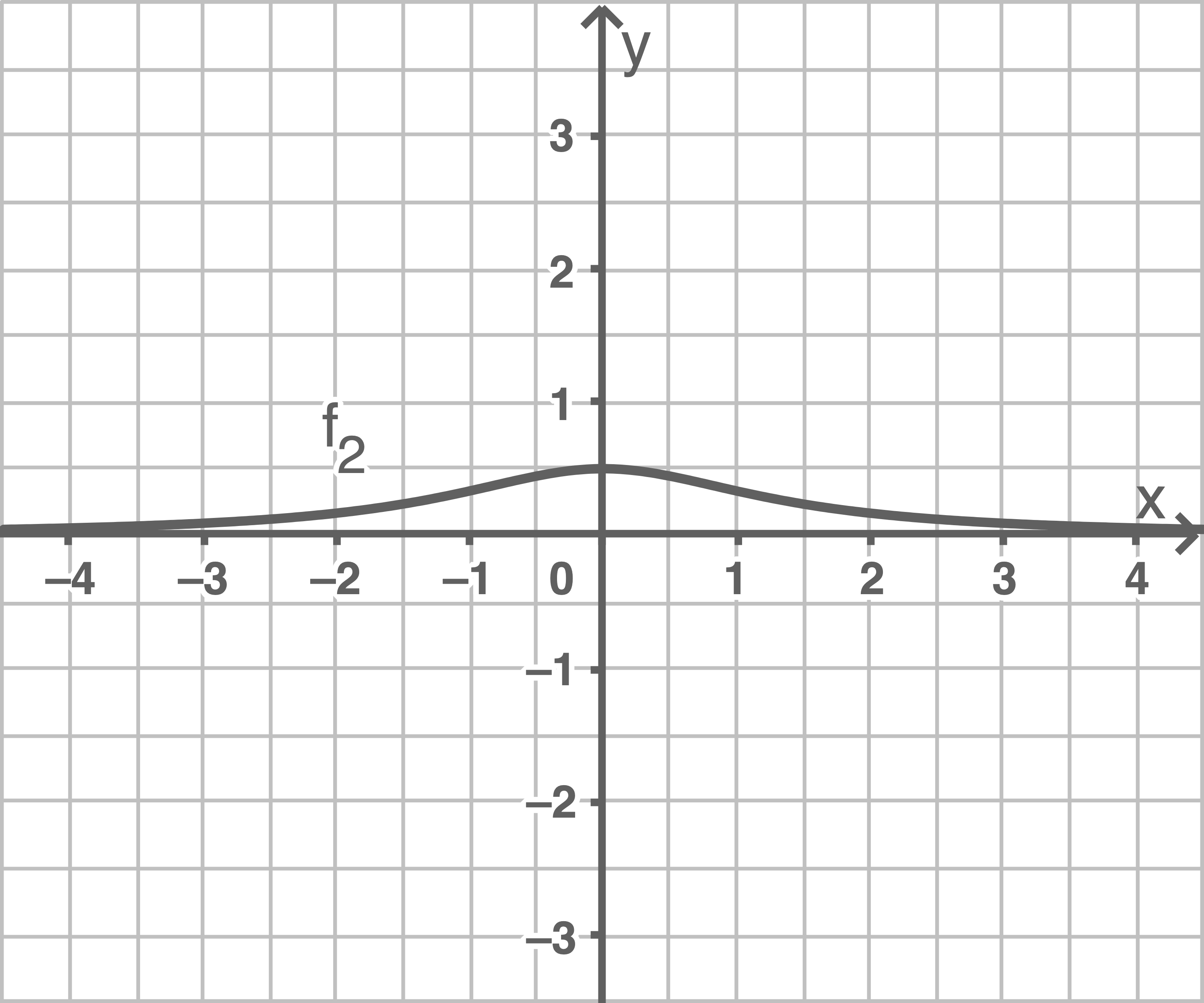
b)
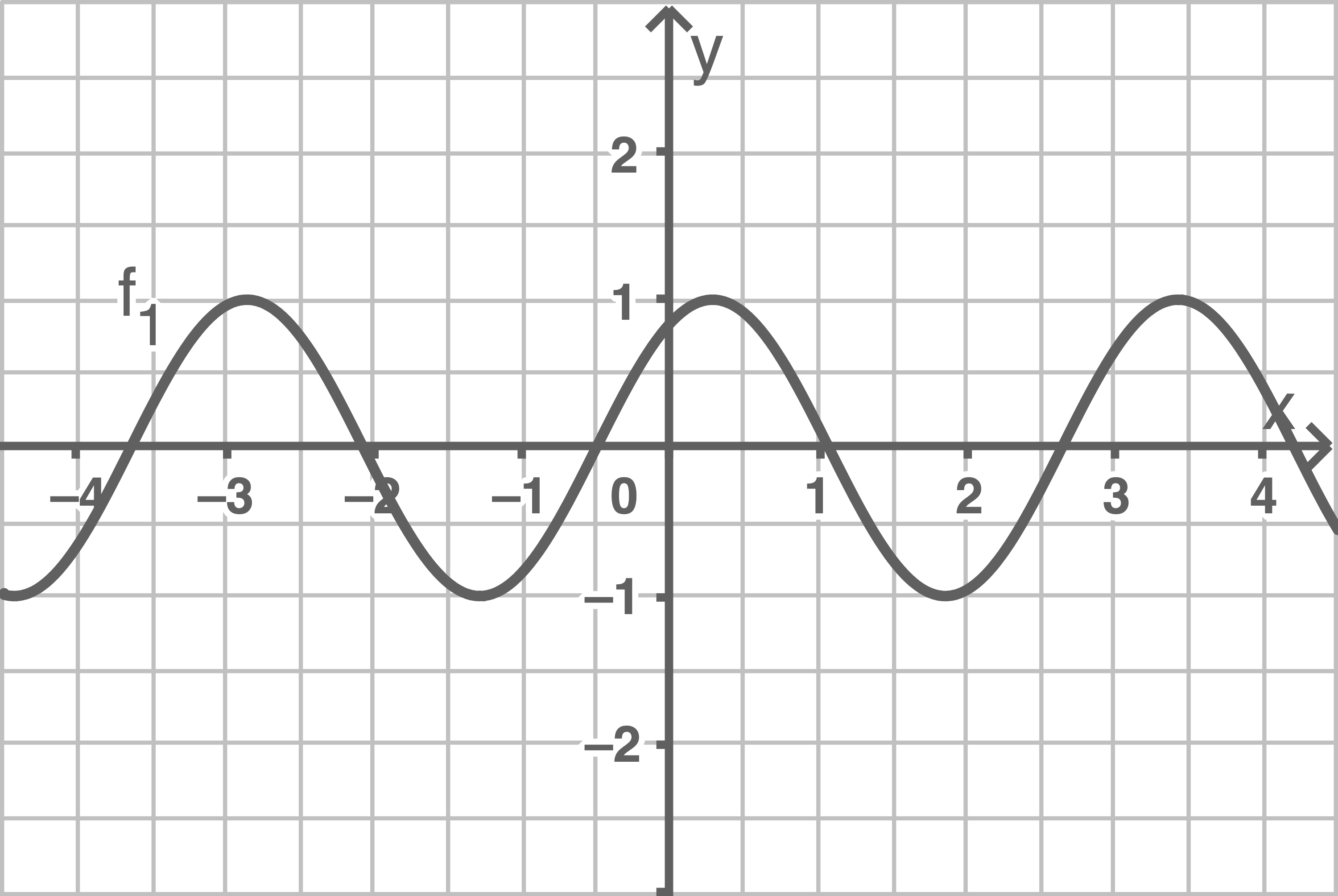
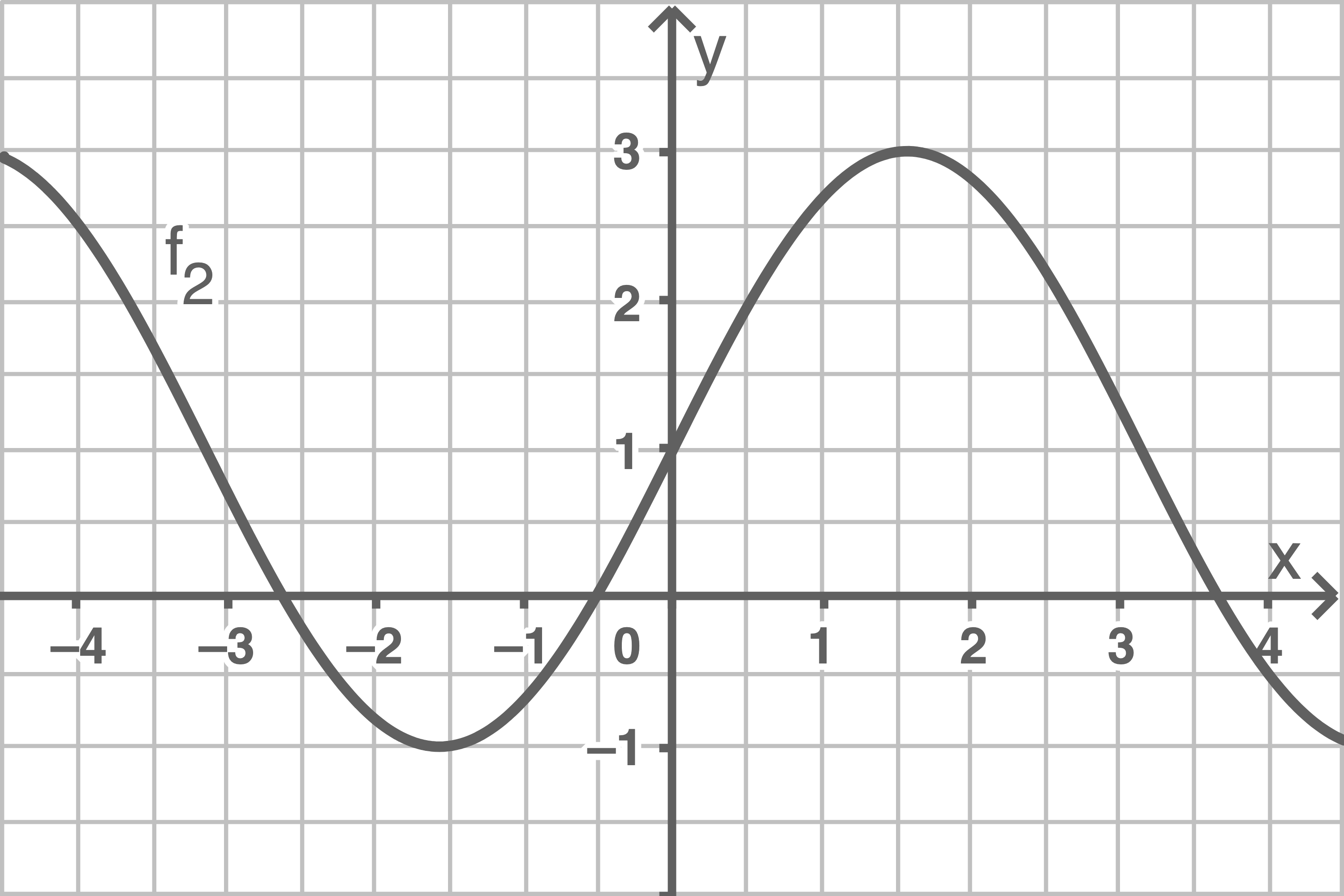
c)
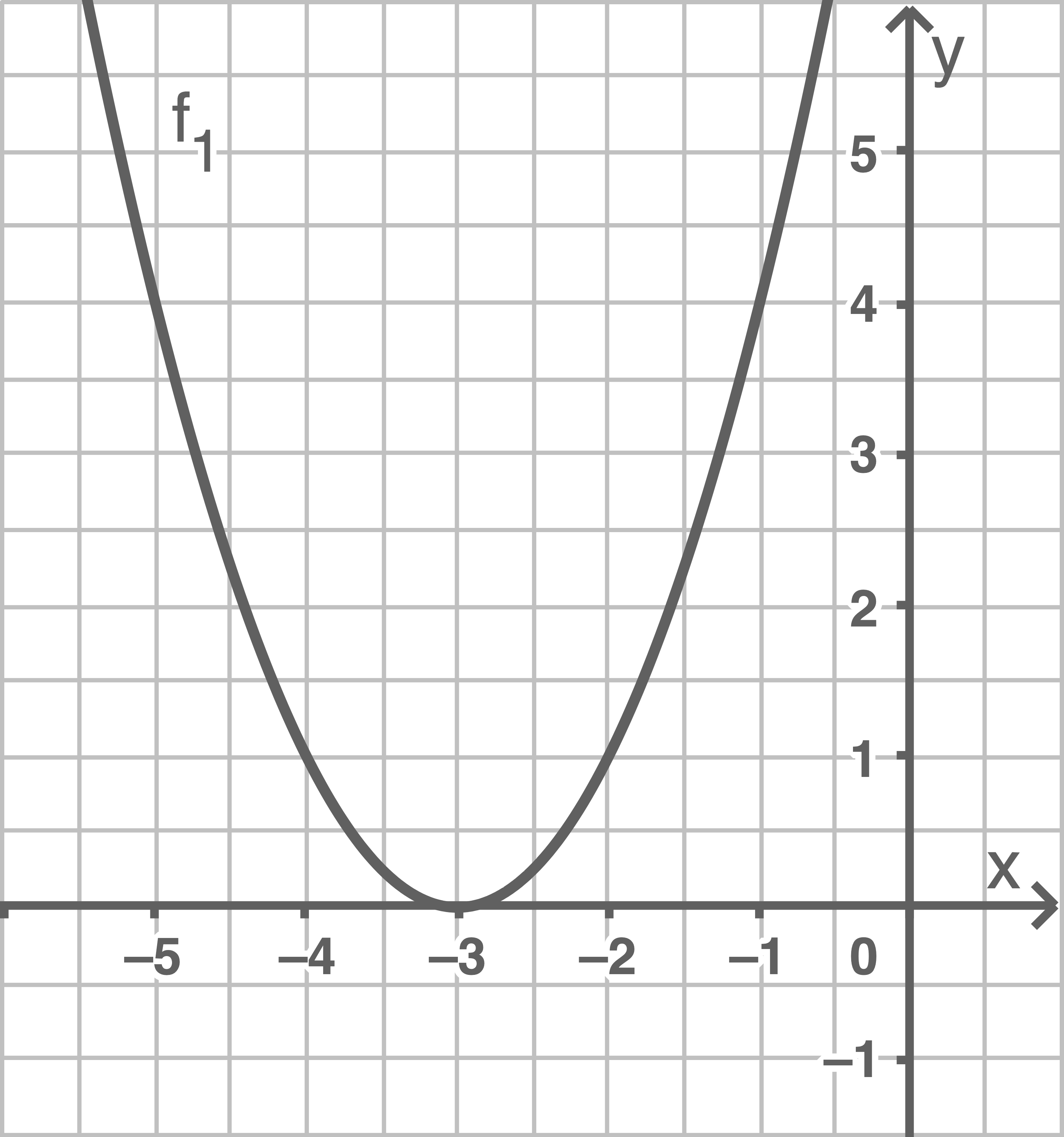
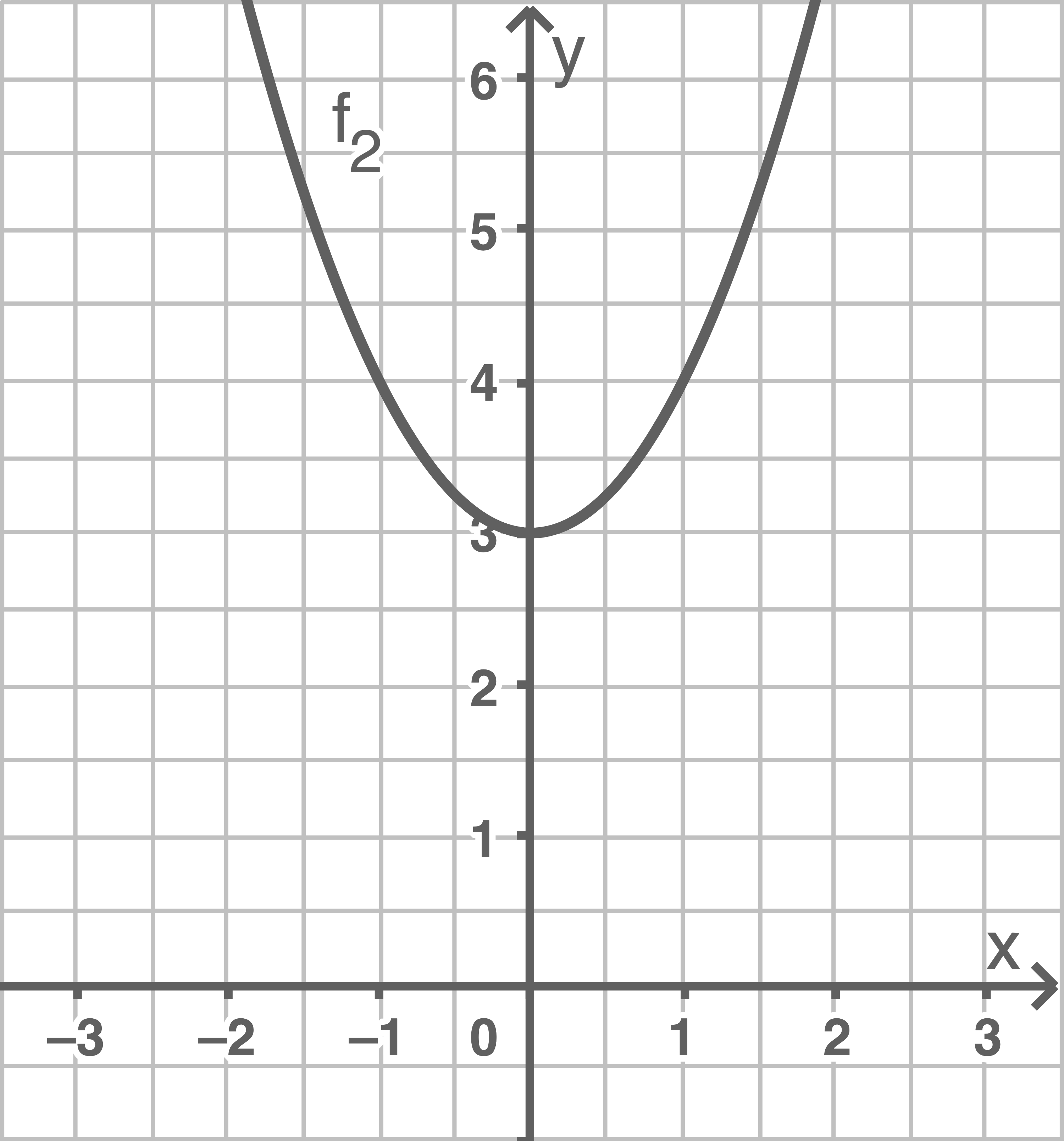
2
a)
b)
c)
d)