Regression
Beim Modellieren von Wachstumsprozessen mittels Funktionen sind die Prognoseergebnisse stark von der Auswahl des Funktionstyps abhängig. Die Entscheidung für einen bestimmten Funktionstyp kann entweder aufgrund des Sachverhalts getroffen werden oder durch die Analyse des Graphenverlaufs über längere Zeiträume erfolgen. Es gibt jedoch Situationen, in denen solche Entscheidungskriterien nicht verfügbar sind.
Beispiel
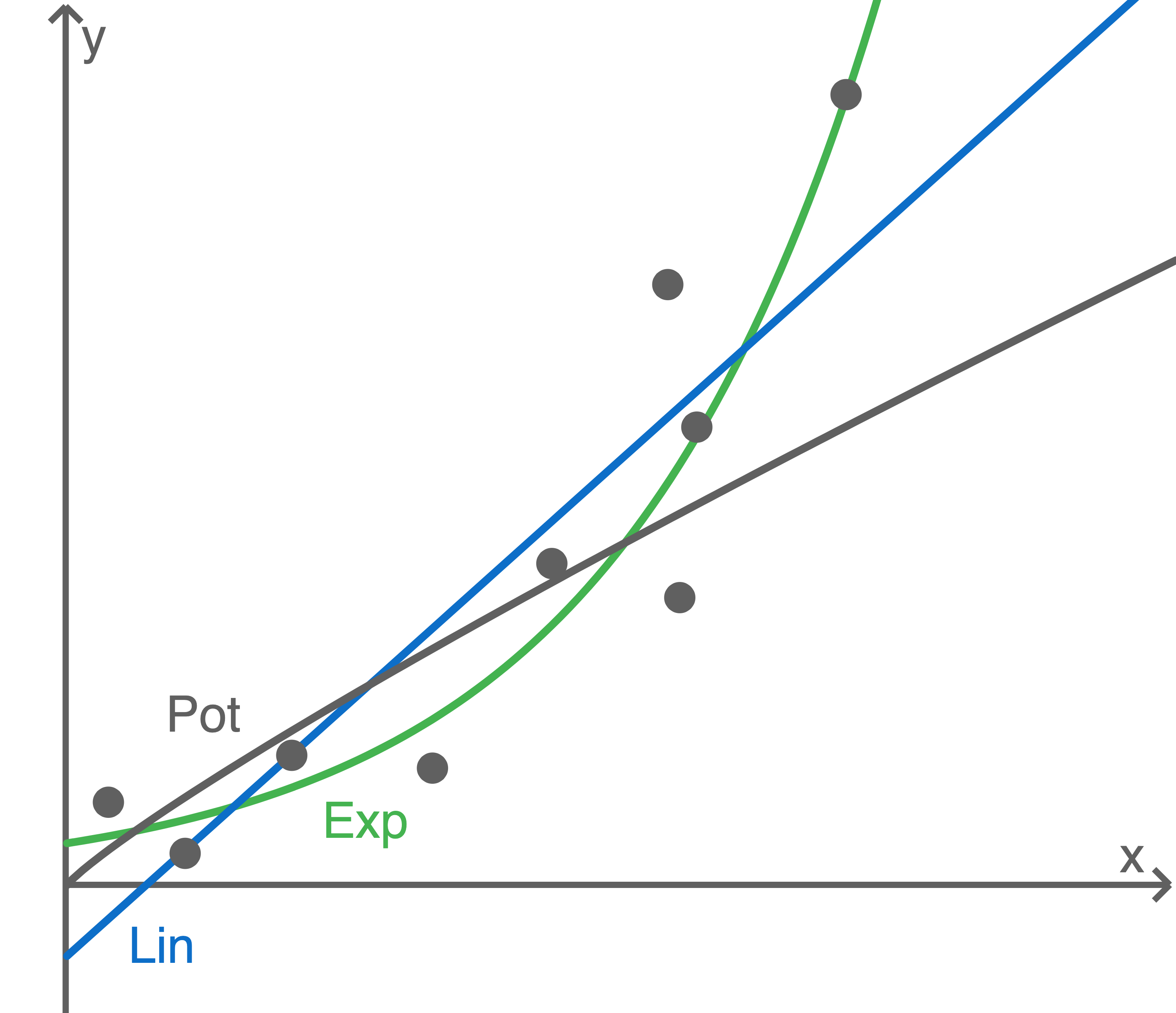
In das Koordinatensystem wurde ein Datensatz eingetragen. Den Daten wurden eine lineare Funktion, eine Potenz- und eine Exponentialfunktion angepasst.
Abhängig vom Funktionstyp variieren die Ergebnisse für Prognosen stark. Für die gegebenen Daten beschreibt die Exponentialfunktion die Daten hier am besten. Je nach Sachzusammenhang sind die Prognosen für weitere Daten jedoch nur für einen bestimmten Zeitraum sinnvoll.
1
Die Weltrekorde der Frauen im Laufen für verschiedene Distanzen sind in der Tabelle auf hundertstel Sekunden genau aufgelistet.
| Distanz | Zeit |
|---|---|
| 100 m | 10,49 |
| 200 m | 21,34 |
| 400 m | 47,60 |
| 800 m | 1:53,28 |
| 1 000 m | 2:28,98 |
a)
Passe den Daten mithilfe des CAS eine lineare Funktion, eine Potenz- und eine Exponentialfunktion an.
b)
Bewerte die Eignung der verschiedenen Funktionstypen zur Beschreibung der Daten.
c)
Die Rekordzeit für 
liegt bei 29:01,03. Hätte man dies durch eine der Regressionen prognostizieren können?
2
Die Siegerzeiten der Männer im 500 m Eisschnelllauf bei den olympischen Winterspielen seit 1972 sind in der Tabelle aufgelistet.
| Winterpiele seit 1972 | Zeit in s |
|---|---|
| 1 | 39,14 |
| 2 | 39,17 |
| 3 | 38,03 |
| 4 | 38,19 |
| 5 | 36,45 |
| 6 | 37,14 |
| 7 | 36,33 |
| 8 | 36,63 |
| 9 | 34,42 |
| 10 | 34,82 |
| 11 | 34,92 |
a)
Ermittle mithilfe des CAS eine Funktion, die die Daten passend beschreibt und begründe die Wahl des Funktionstyps.
b)
Die Siegerzeit für 2022, also die 12. olympischen Winterspiele seit 1978, liegt bei 34,61 Sekunden. Passt dieser Wert zu der ermittelten Funktion?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
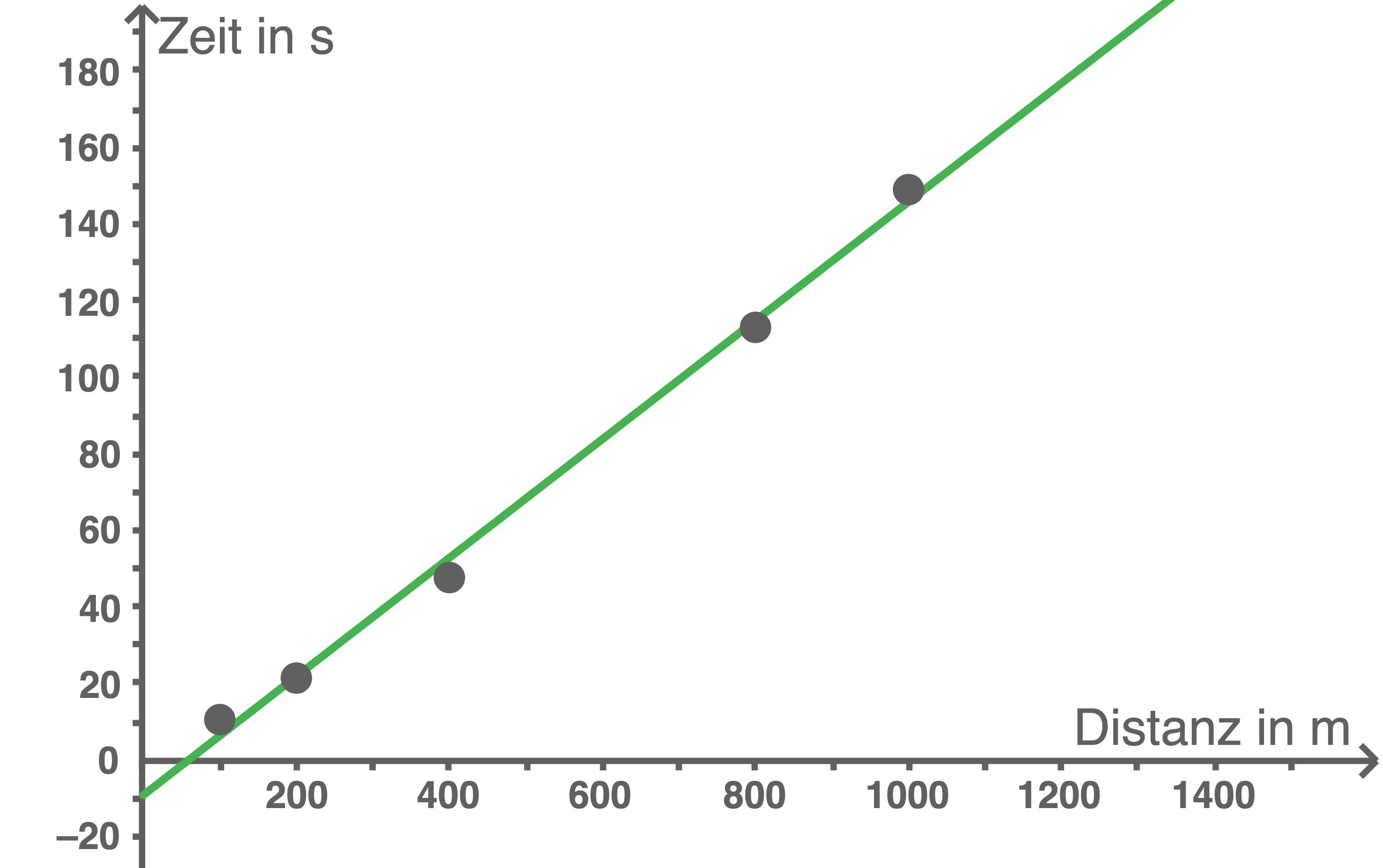
Lineare Funktion
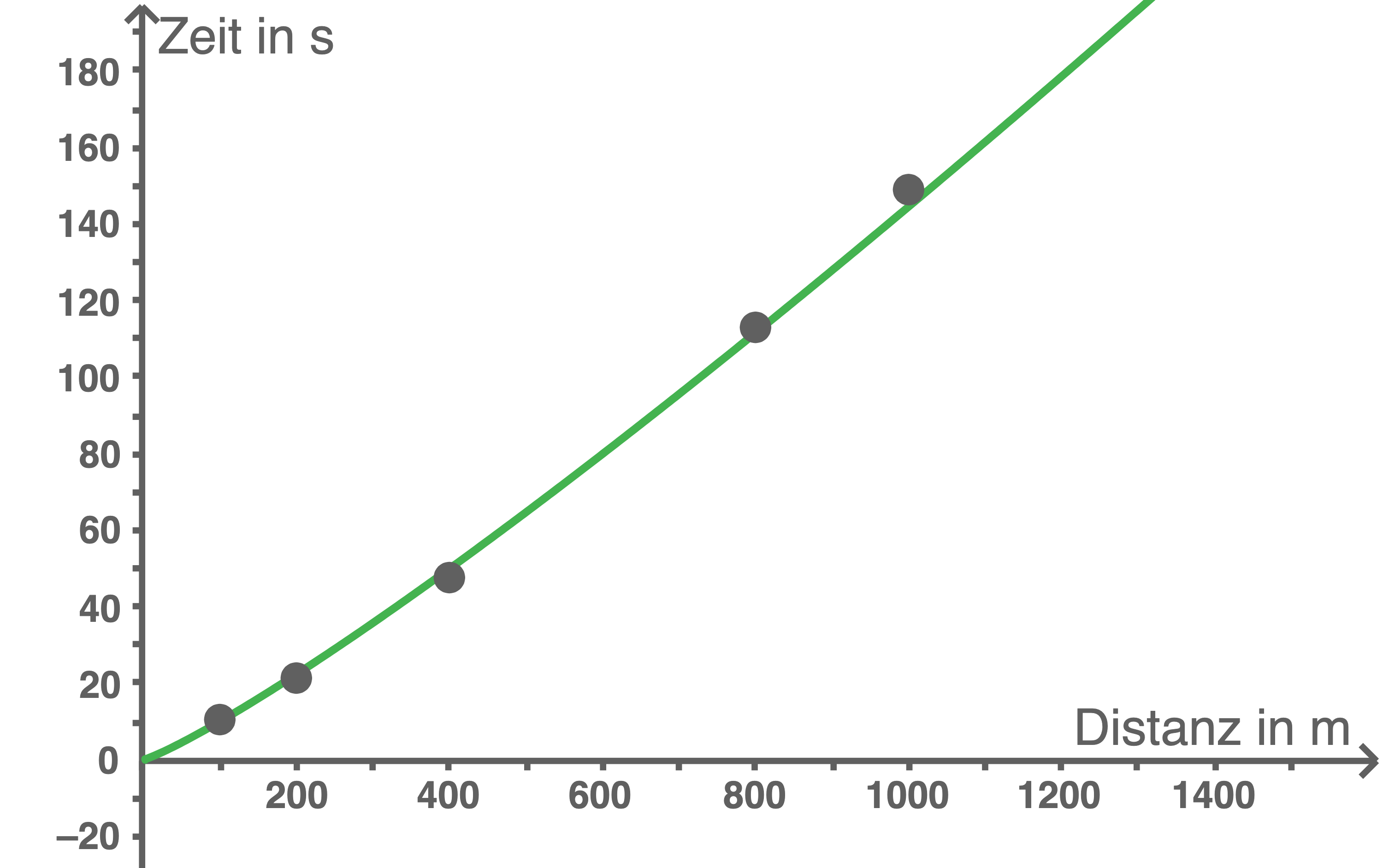
Potenzfunktion
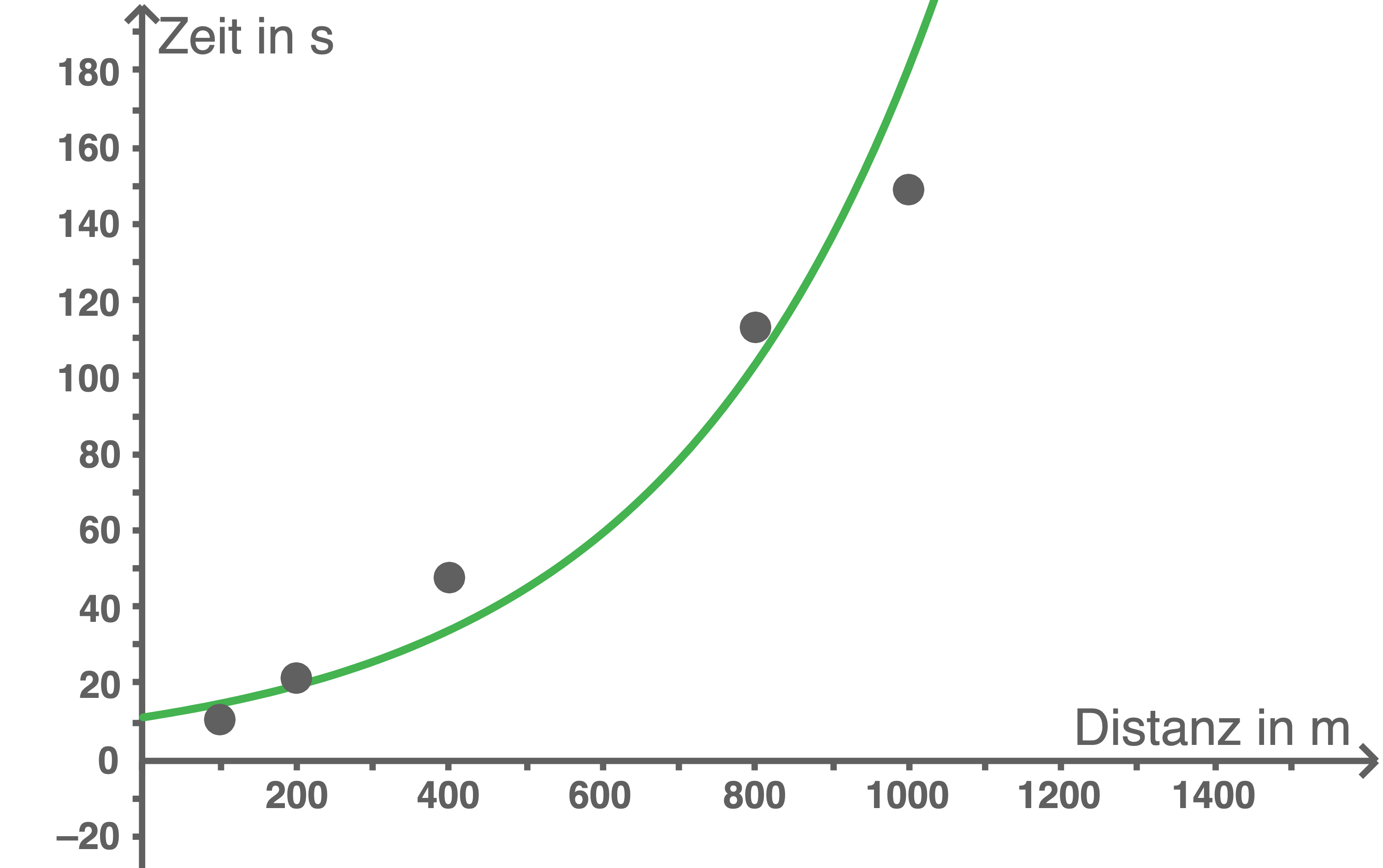
Exponentialfunktion
b)
An den Daten ist bereits zu erkennen, dass kein lineares Wachstum vorliegt. Dennoch werden die Daten recht gut durch die lineare Funktion beschrieben. Für größere Distanzen sind jedoch Abweichungen zu erwarten und auch die negativen Werte für kleine Distanzen passen nicht in den Sachzusammenhang.
Die Potenzfunktion beschreibt die Daten recht genau und passt auch von der Tendenz zu den bekannten Werten.
Die Exponentialfunktion beschreibt die Daten im Vergleich zu den anderen beiden Funktionstypen eher ungenau. Auch für Prognosen für größere Distanzen ist der Graph der Funktion zu steil und passt nicht zum Trend der Daten.
c)
Der Wert der Funktion 
an der Stelle 
ist viel zu groß. Für die Funktionen 
und 
gilt:
Die Rekordzeit liegt bei 
Diese Zeit wurde von keiner der Funktionen prognostiziert, liegt aber zwischen den Prognosen der linearen Funktion und der Potenzfunktion.
2
a)
Die Daten können durch eine Potenzfunktion beschrieben werden. Sowohl für eine lineare Funktion als auch eine Exponentialfunktion fällt der zugehörige Graph zu schnell ab. Auch bei der Potenzfunktion wird es ab einem gewissen Punkt nicht mehr möglich sein, eine immer bessere Zeit zu erreichen, jedoch wird dieser Zeitpunkt deutlich später als bei den anderen beiden Funktionstypen erreicht.
Das CAS liefert 
b)