Zahlenfolgen
Definition
Eine Zahlenfolge (kurz Folge) ist eine Funktion, deren Definitionsbereich die Menge der natürlichen ZahlenRekursive und explizite Vorgabe
Beispiel: Zahlenfolge der ungeraden Zahlen:
1
Gib die ersten 5 Folgenglieder an und zeichne den Graphen.



![\(a_n=\sqrt[n]{3}\)](https://mathjax.schullv.de/06d7b3cc03949ced803587a2e5d4f99b0d2c39f1c7e0a7a344faf741a3b6c0ea?color=5a5a5a)
a)
b)
c)
d)
2
Gib für die Folge den expliziten und den rekursiven Funktionsterm an.




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
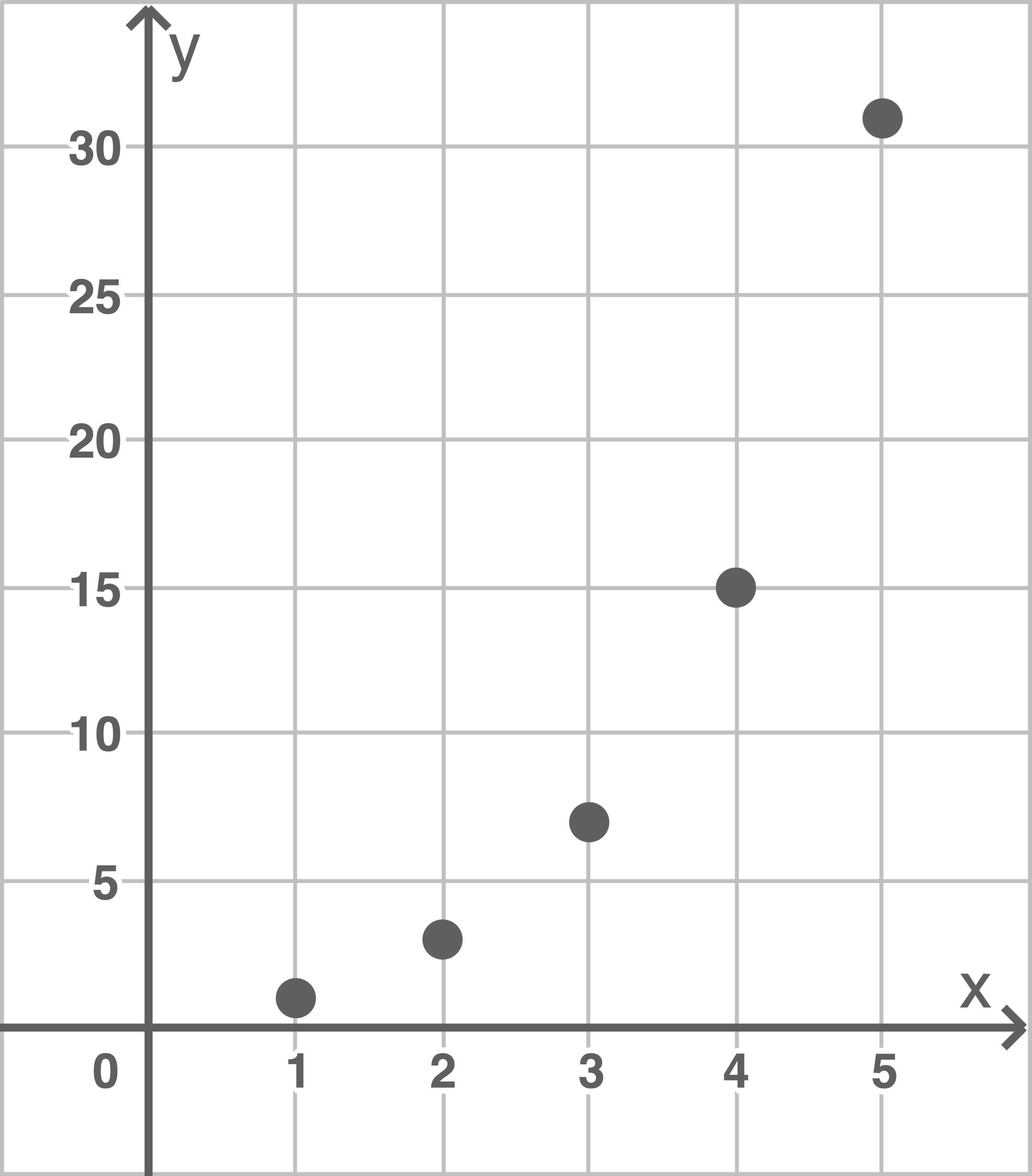
b)
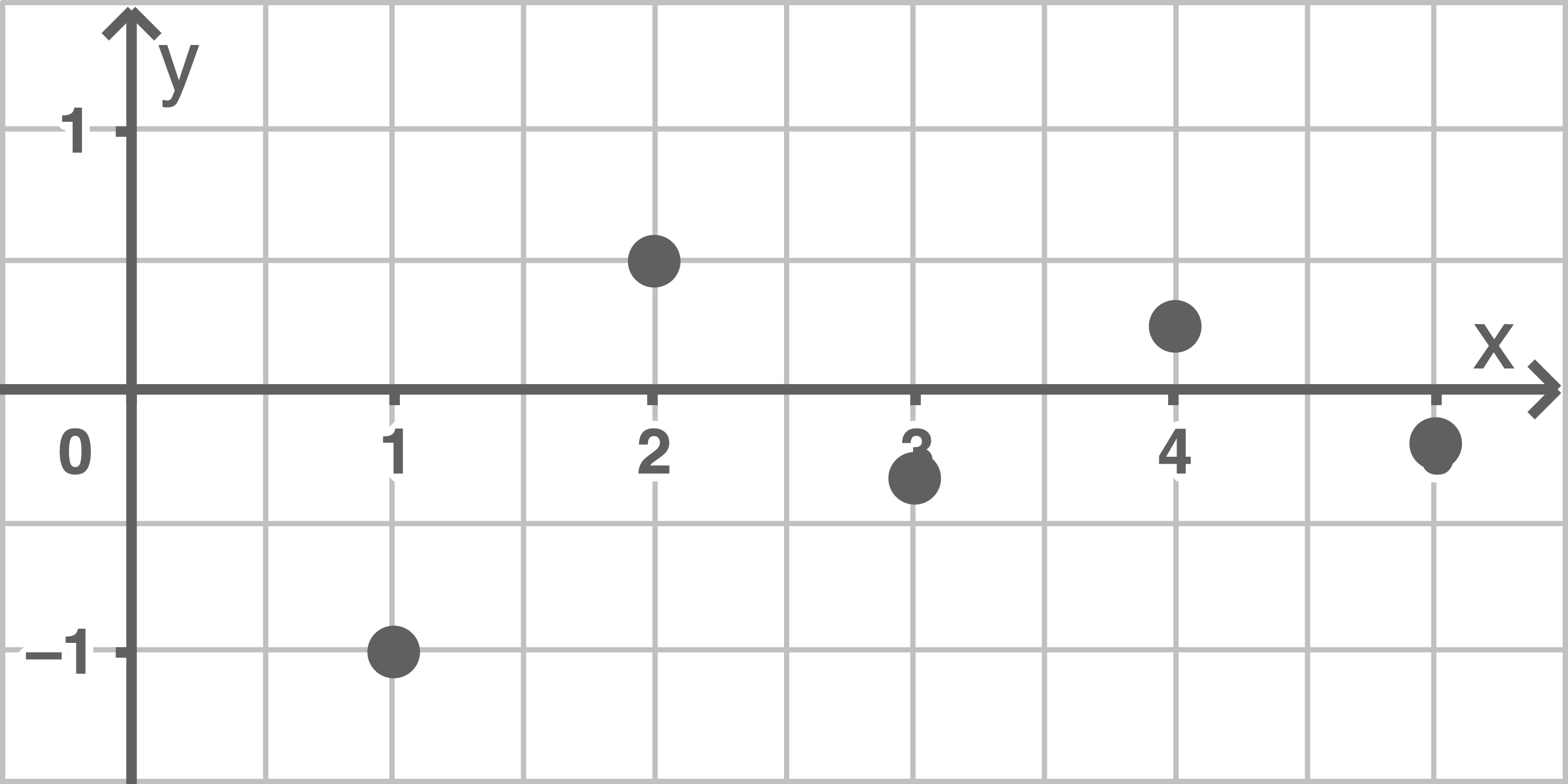
c)
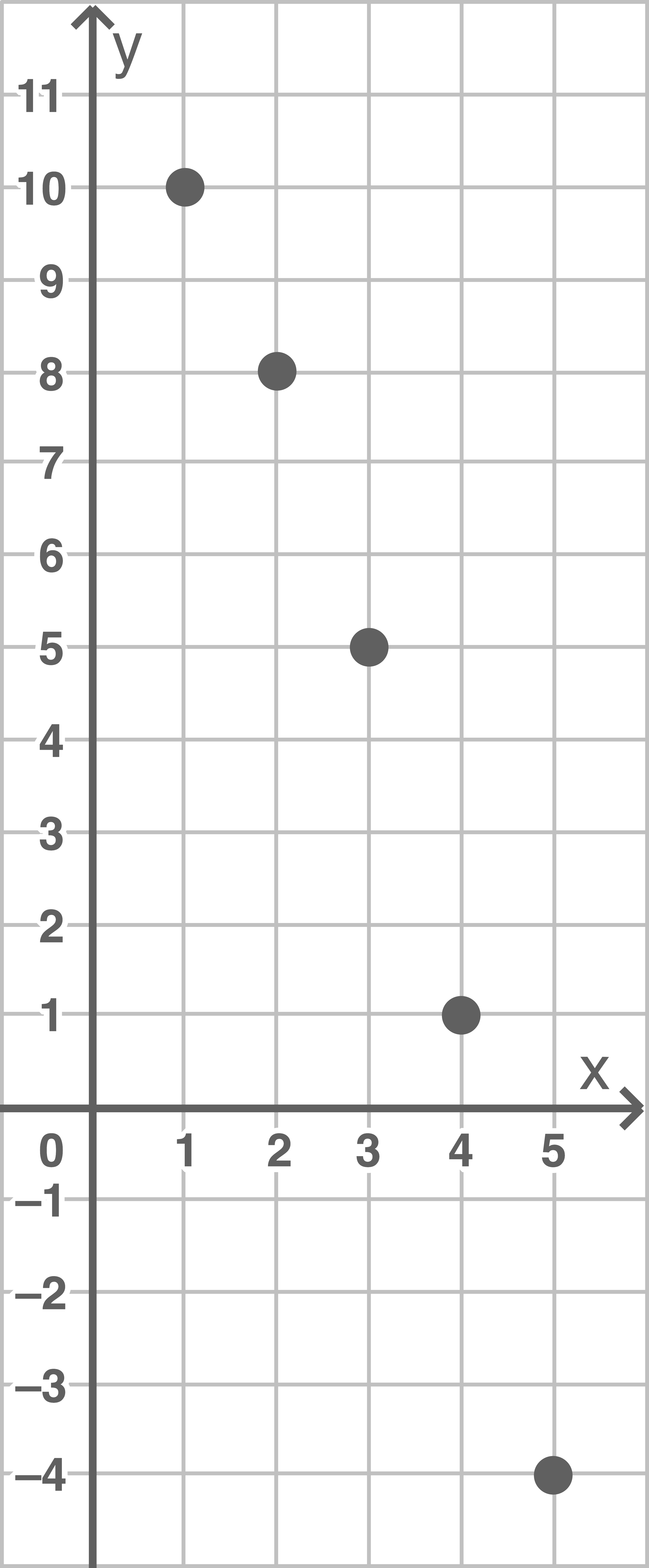
d)
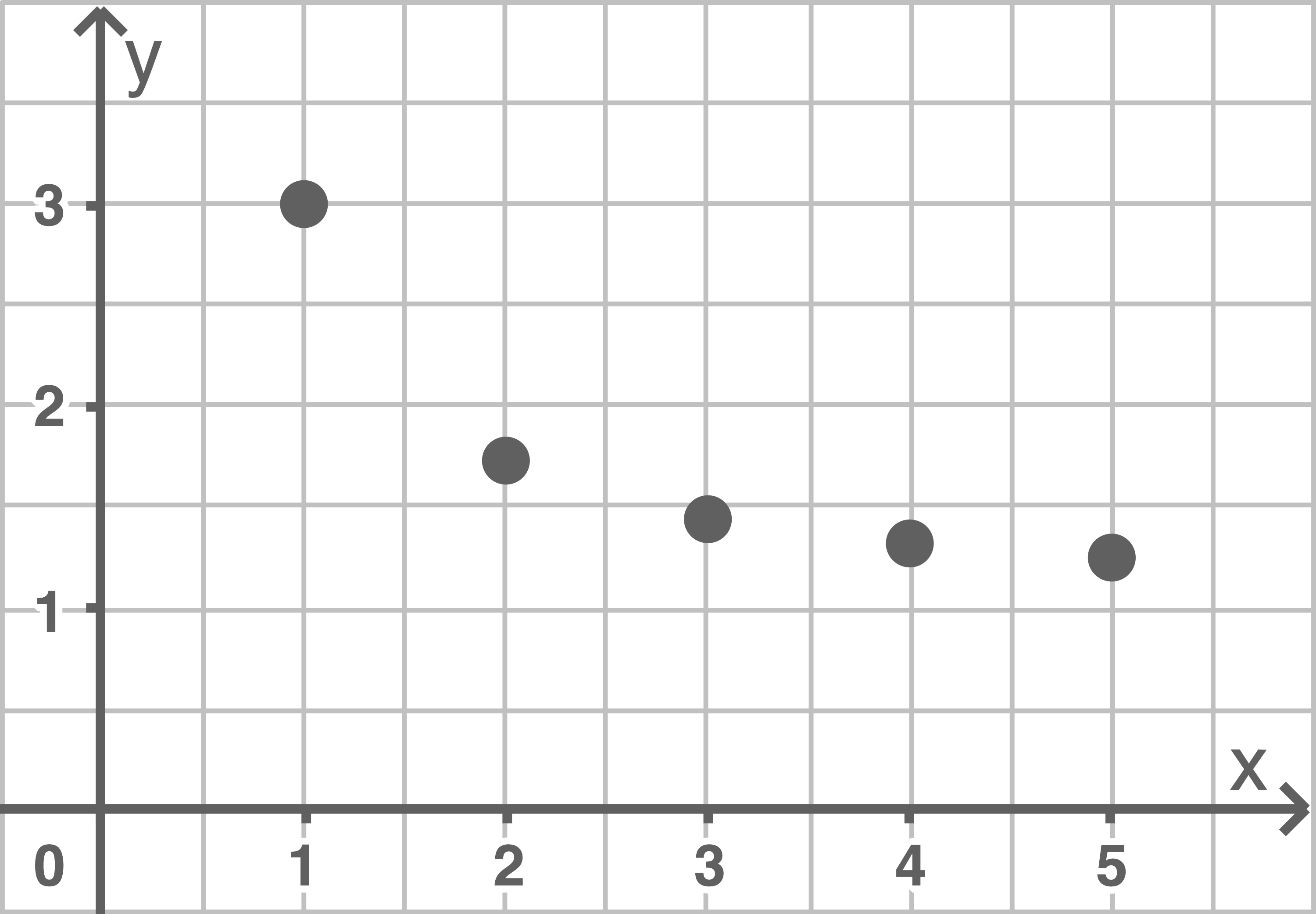
2
a)
explizit:  rekursiv:
rekursiv: 
b)
explizit:  rekursiv:
rekursiv: 
c)
explizit:  rekursiv:
rekursiv: 
d)
explizit:  rekursiv:
rekursiv: 