Wahrscheinlichkeitsverteilung und Erwartungswert
Zufallsgröße
Bei einem Zufallsversuch wird jedem Ergebnis ein Wert zugeordnet. Diese Zuordnung wird als Zufallsgröße bezeichnet. Zufallsgrößen werden oft mitBeispiel
Wird bei einem Glücksrad die ZahlErwartungswert einer Zufallsgröße
Der Mittelwert für die Wahrscheinlichkeitsverteilung einer Zufallsgröße wird Erwartungswert genannt. Wenn eine Zufallsgröße
1
Zwei Würfel werden geworfen. Dabei wird die Zufallsgröße  betrachtet.
betrachtet.
Bestimme die Wahrscheinlichkeiten folgender Ereignisse:
Bestimme die Wahrscheinlichkeiten folgender Ereignisse:
- Augensumme größer als
und kleiner als
- Augensumme mindestens
- Augensumme höchstens
2
Eine Münze wird dreimal geworfen. Dabei wird gezählt, wie oft „Zahl“ fällt.
Zeichne ein Baumdiagramm und bestimme die Wahrscheinlichkeit für folgende Ereignisse:
Zeichne ein Baumdiagramm und bestimme die Wahrscheinlichkeit für folgende Ereignisse:
- Dreimal „Zahl“
- Zweimal „Zahl“
- Keinmal „Zahl“
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
| EINS | ZWEI | DREI | VIER | FÜNF | SECHS | |
|---|---|---|---|---|---|---|
| EINS | 2 | 3 | 4 | 5 | 6 | 7 |
| ZWEI | 3 | 4 | 5 | 6 | 7 | 8 |
| DREI | 4 | 5 | 6 | 7 | 8 | 9 |
| VIER | 5 | 6 | 7 | 8 | 9 | 10 |
| FÜNF | 6 | 7 | 8 | 9 | 10 | 11 |
| SECHS | 7 | 8 | 9 | 10 | 11 | 12 |
| Wert Zufallsgröße | Wahrscheinlichkeit |
|---|---|
2
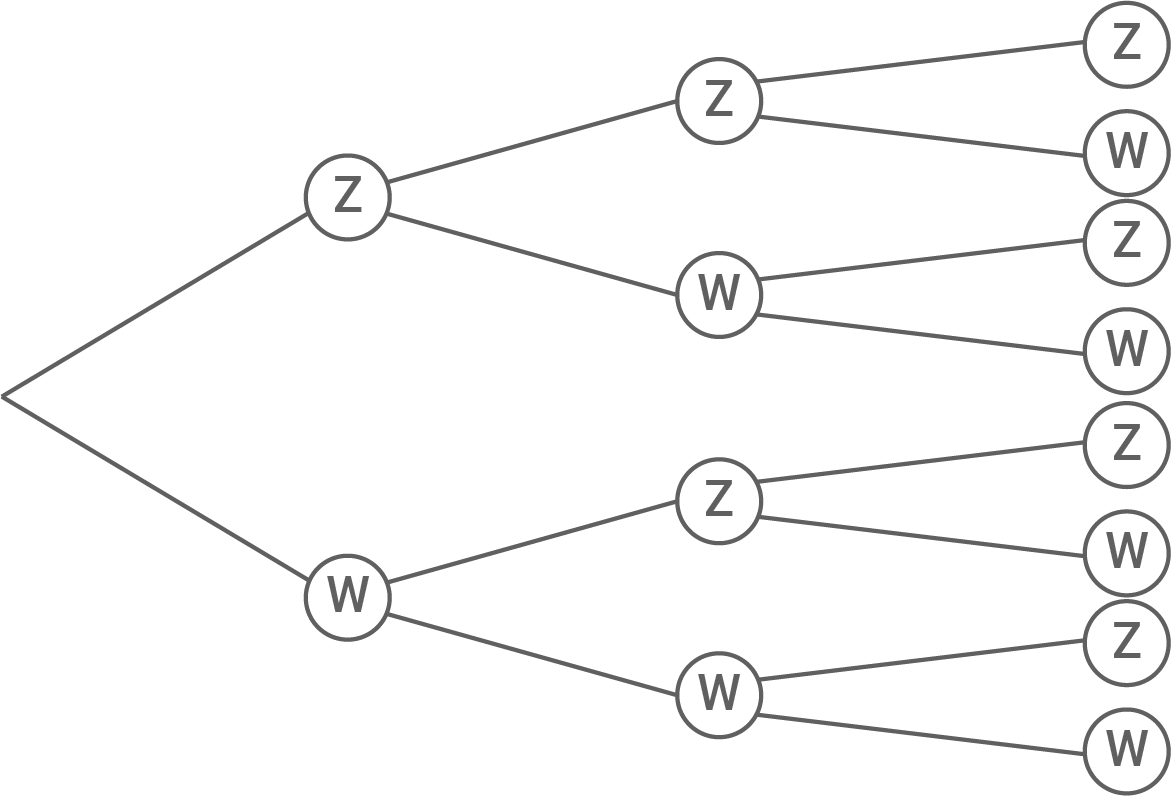
| Wert Zufallsgröße | Wahrscheinlichkeit |
|---|---|
| ZZZ | |
| ZZW | |
| ZWZ | |
| ZWW | |
| WZZ | |
| WZW | |
| WWZ | |
| WWW |