Schranken einer Folge
Definition
Eine Folge hat eine obere/untere SchrankeBeispiel
Der Graph der Folge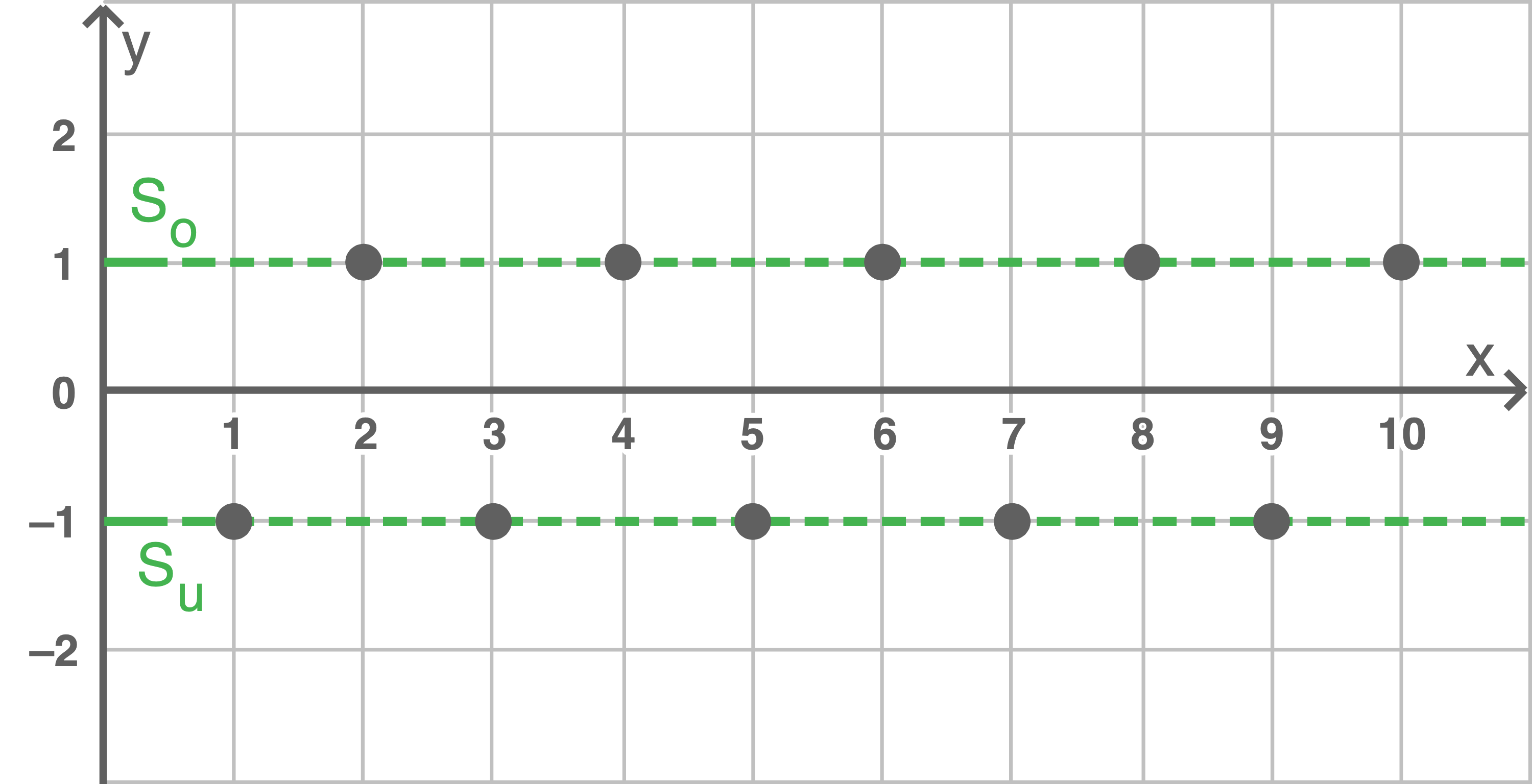
1
Entscheide, ob die Folge nach oben oder nach unten beschränkt ist. Falls ja, gib die kleinste obere oder die größte untere sowie eine weitere obere bzw. untere Schranke an.




a)
b)
c)
d)
2
Gib jeweils eine Folge mit den angegebenen Eigenschaften an.
 ist eine obere Schranke,
ist eine obere Schranke,  aber nicht.
aber nicht.
 ist die größte untere Schranke, aber es gibt kein Folgenglied mit
ist die größte untere Schranke, aber es gibt kein Folgenglied mit 
 ist gleichzeitig obere und untere Schranke.
ist gleichzeitig obere und untere Schranke.
a)
b)
c)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Da die Folge für  startet und die Folgenglieder immer größer werden, ist
startet und die Folgenglieder immer größer werden, ist  nach unten beschränkt.
Größte untere Schranke:
nach unten beschränkt.
Größte untere Schranke: 
Weitere untere Schranke:
Weitere untere Schranke:
b)
Die Folge ist sowohl nach oben als auch nach unten beschränkt, da von  eine immer kleiner werdende Zahl abgezogen wird.
Größte untere Schranke:
eine immer kleiner werdende Zahl abgezogen wird.
Größte untere Schranke: 
Weitere untere Schranke: Kleinste obere Schranke:
Kleinste obere Schranke: 
Weitere obere Schranke:
Weitere untere Schranke:
Weitere obere Schranke:
c)
Die Folge ist sowohl nach oben als auch nach unten beschränkt, da die Folgenglieder nur die Werte  und
und  annehmen.
Größte untere Schranke:
annehmen.
Größte untere Schranke: 
Weitere untere Schranke: Kleinste obere Schranke:
Kleinste obere Schranke: 
Weitere obere Schranke:
Weitere untere Schranke:
Weitere obere Schranke:
d)
Die Folge ist sowohl nach oben als auch nach unten beschränkt, da sich die Folgenglieder immer weiter dem Wert  annähern.
Größte untere Schranke:
annähern.
Größte untere Schranke: 
Weitere untere Schranke: Kleinste obere Schranke:
Kleinste obere Schranke: 
Weitere obere Schranke:
Weitere untere Schranke:
Weitere obere Schranke:
2
a)
b)
c)