Graphen der Exponentialfunktionen verschieben und strecken
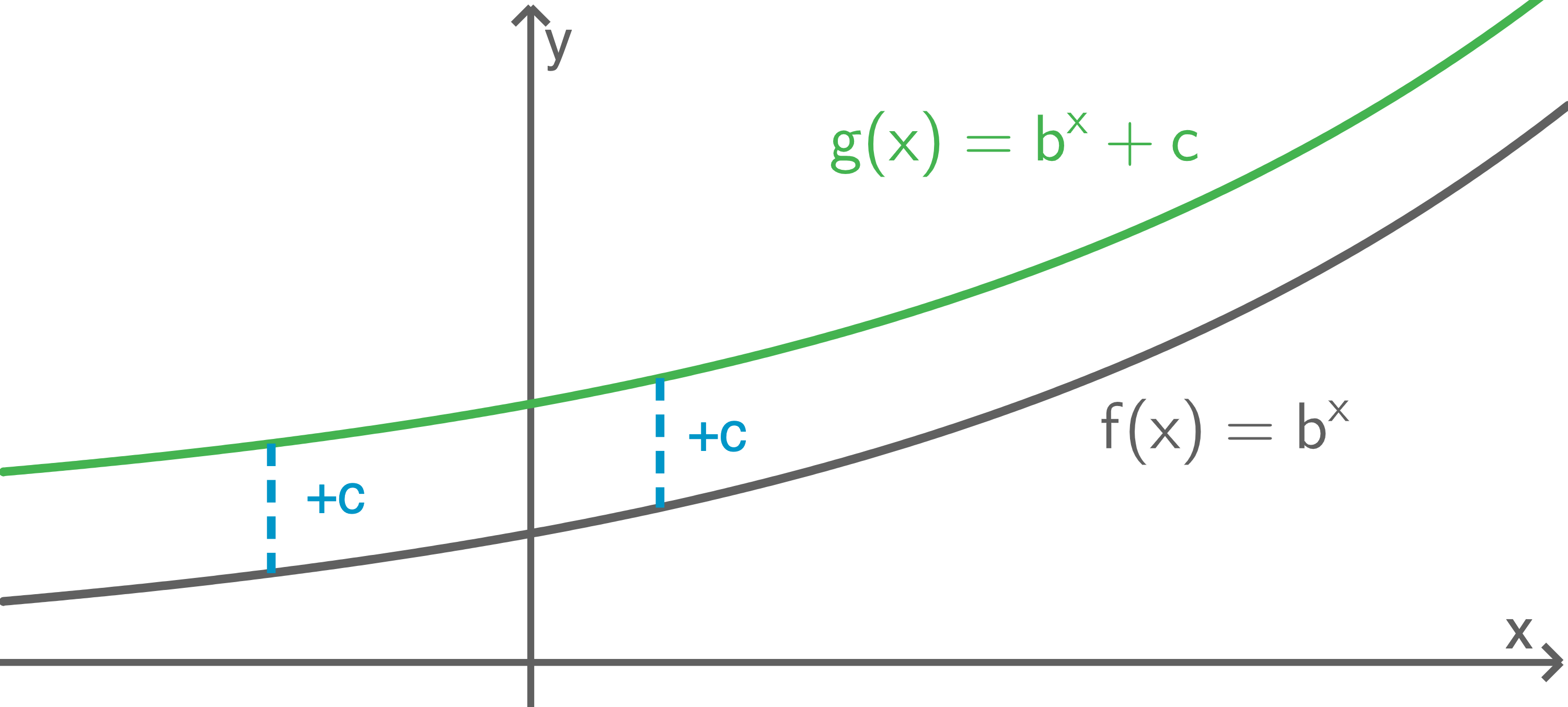
Verschieben entlang der y-Achse
Der Graph der Funktion  ergibt sich aus dem Graphen der Funktion
ergibt sich aus dem Graphen der Funktion  durch Verschieben um
durch Verschieben um  Einheiten entlang der
Einheiten entlang der  -Achse, und zwar
-Achse, und zwar
- für
nach unten.
- für
nach oben.
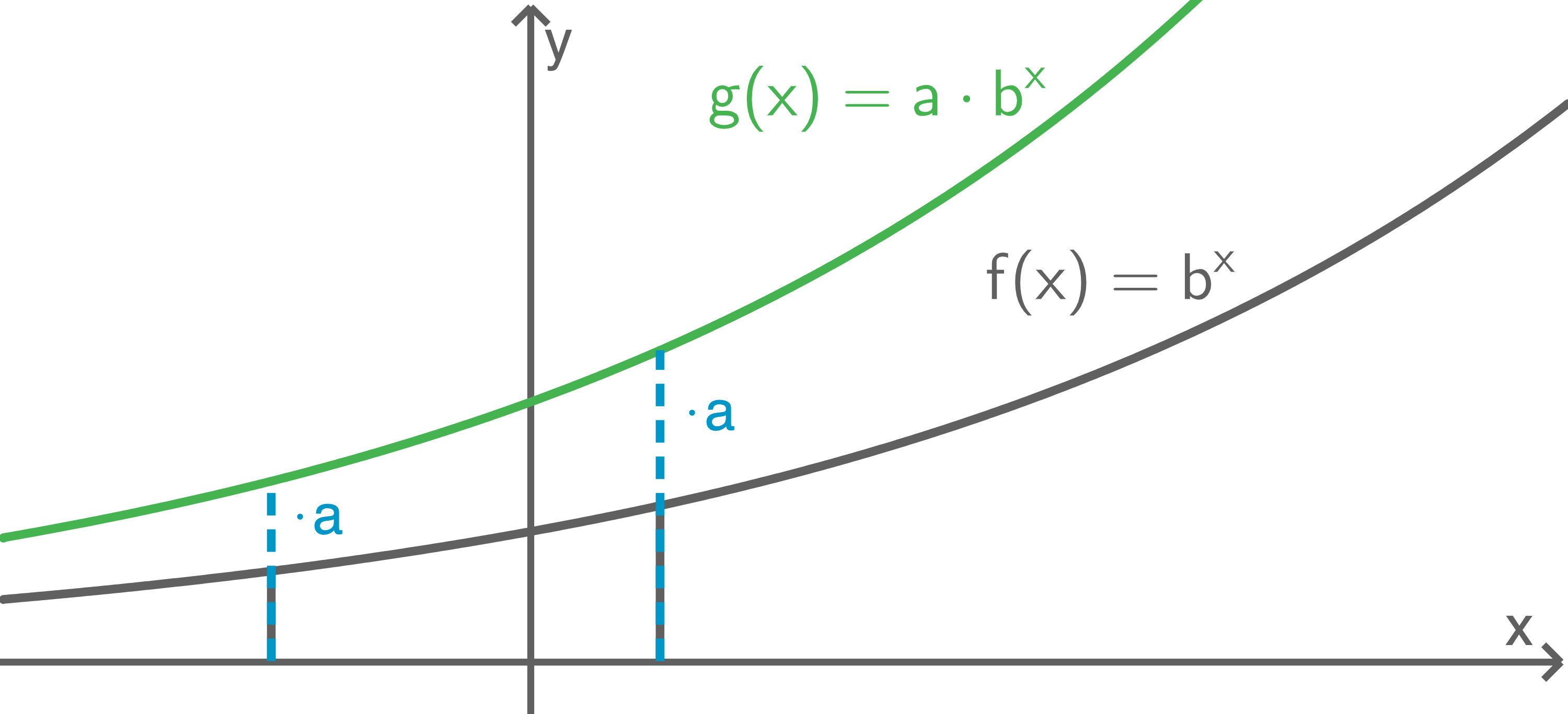
Strecken entlang der y-Achse
Der Graph der Funktion  ergibt sich aus dem Graphen der Funktion
ergibt sich aus dem Graphen der Funktion  durch Strecken mit dem Faktor
durch Strecken mit dem Faktor  entlang der
entlang der  -Achse.
Bei einem negativen Streckfaktor
-Achse.
Bei einem negativen Streckfaktor  wird der Graph zusätzlich an der
wird der Graph zusätzlich an der  -Achse gespiegelt.
-Achse gespiegelt.
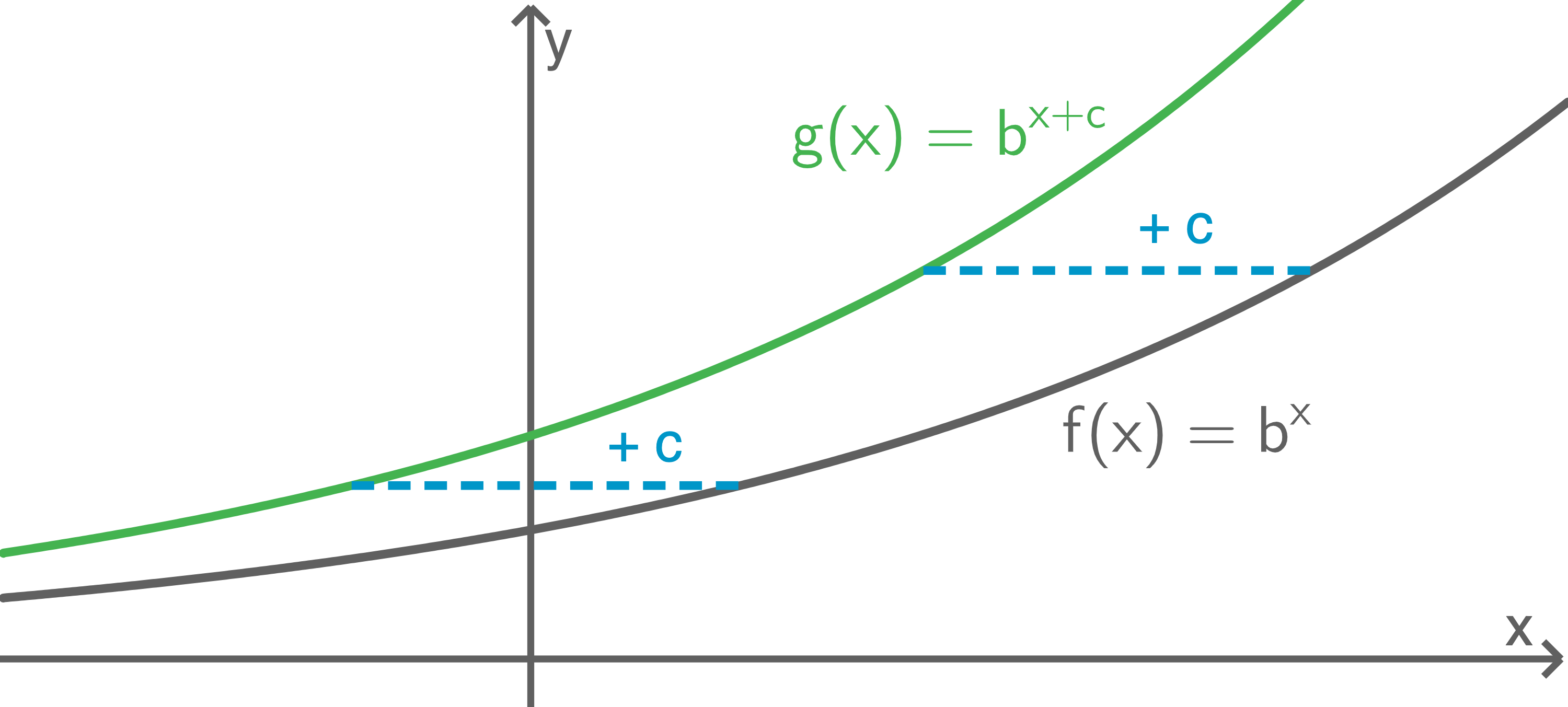
Verschieben entlang der x-Achse
Der Graph der Funktion  ergibt sich aus dem Graphen der Funktion
ergibt sich aus dem Graphen der Funktion  durch Verschieben um
durch Verschieben um  Einheiten entlang der
Einheiten entlang der  -Achse, und zwar
-Achse, und zwar
- für
nach rechts.
- für
nach links.
Zusammenhang Verschiebung und Streckung
Der Graph der Funktion- Verschieben entlag der
-Achse um
Einheiten
- Strecken entlang der
-Achse mit dem Faktor
:
1
Zeichne den Graphen der Funktion  Zeichne in das gleiche Koordinatensystem den Graphen zu:
Zeichne in das gleiche Koordinatensystem den Graphen zu:




a)
b)
c)
d)
2
Bestimme die Funktionsgleichung. Der Graph der Exponentialfunktion zur Basis  wird
wird
a)
an der  -Achse gespiegelt.
-Achse gespiegelt.
b)
entlang der  -Achse um eine Einheit nach rechts verschoben.
-Achse um eine Einheit nach rechts verschoben.
c)
entlang der  -Achse um
-Achse um  Einheiten nach unten verschoben.
Einheiten nach unten verschoben.
d)
an der  -Achse gespiegelt und anschließend um eine Einheit nach links und um
-Achse gespiegelt und anschließend um eine Einheit nach links und um  Einheiten nach oben verschoben.
Einheiten nach oben verschoben.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
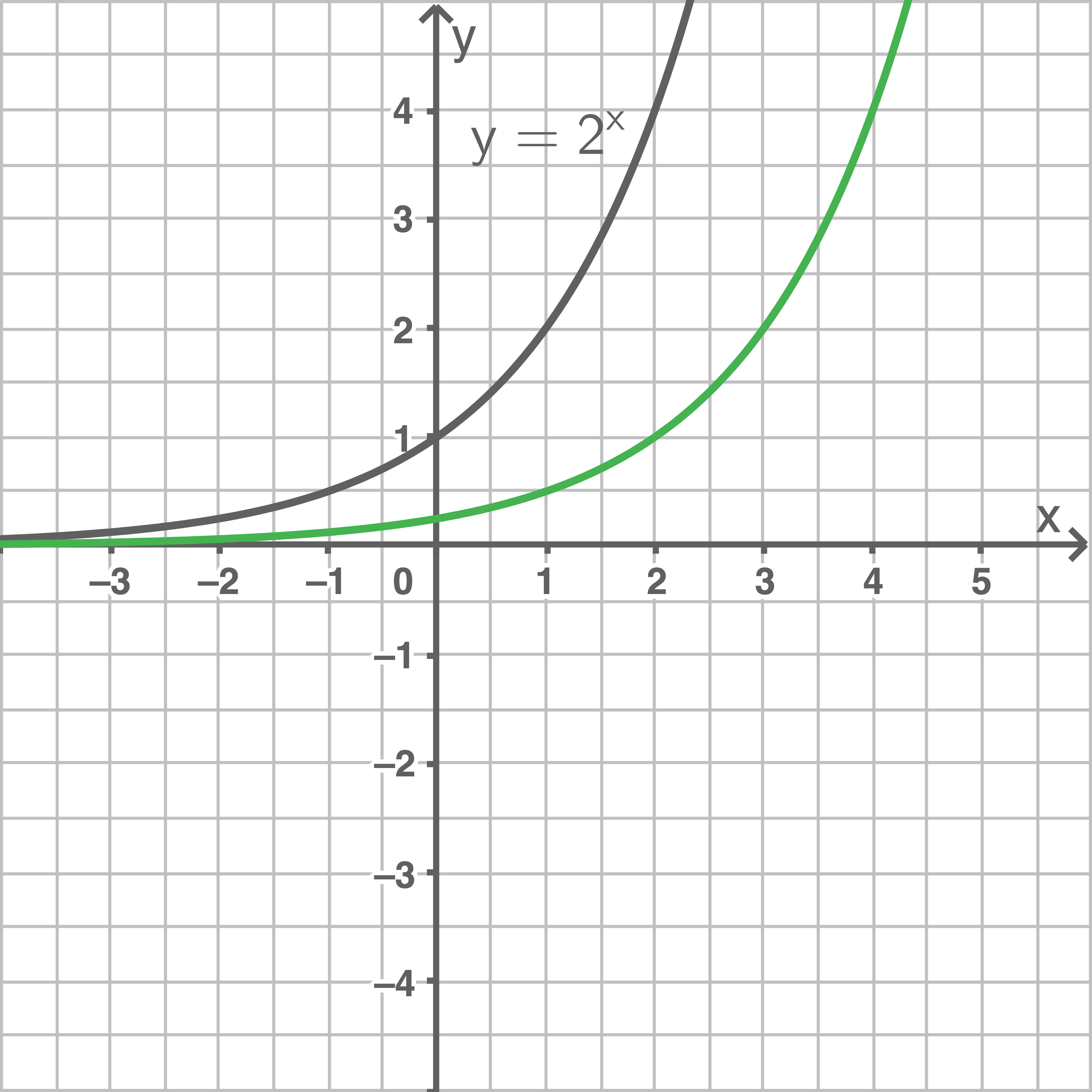
b)
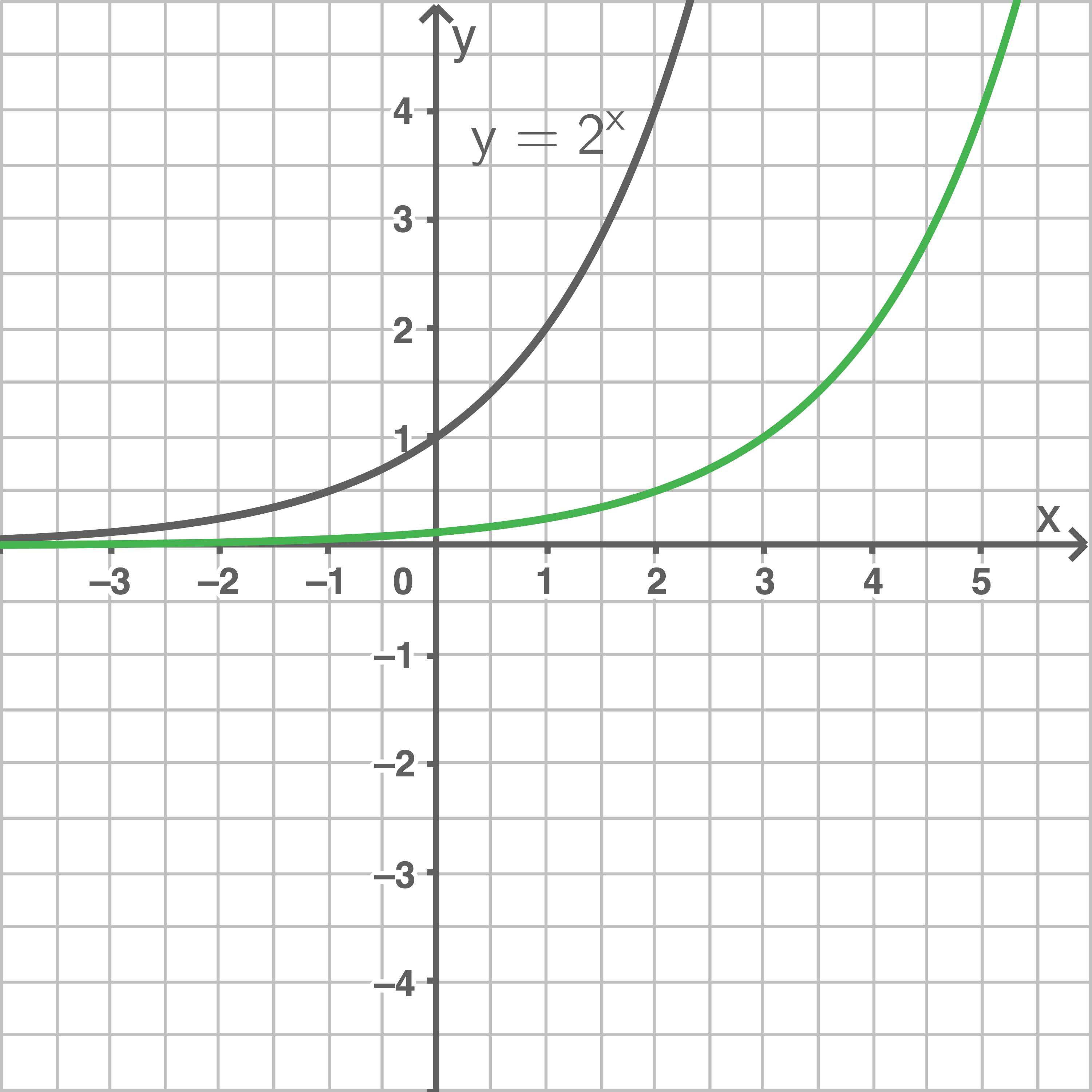
c)
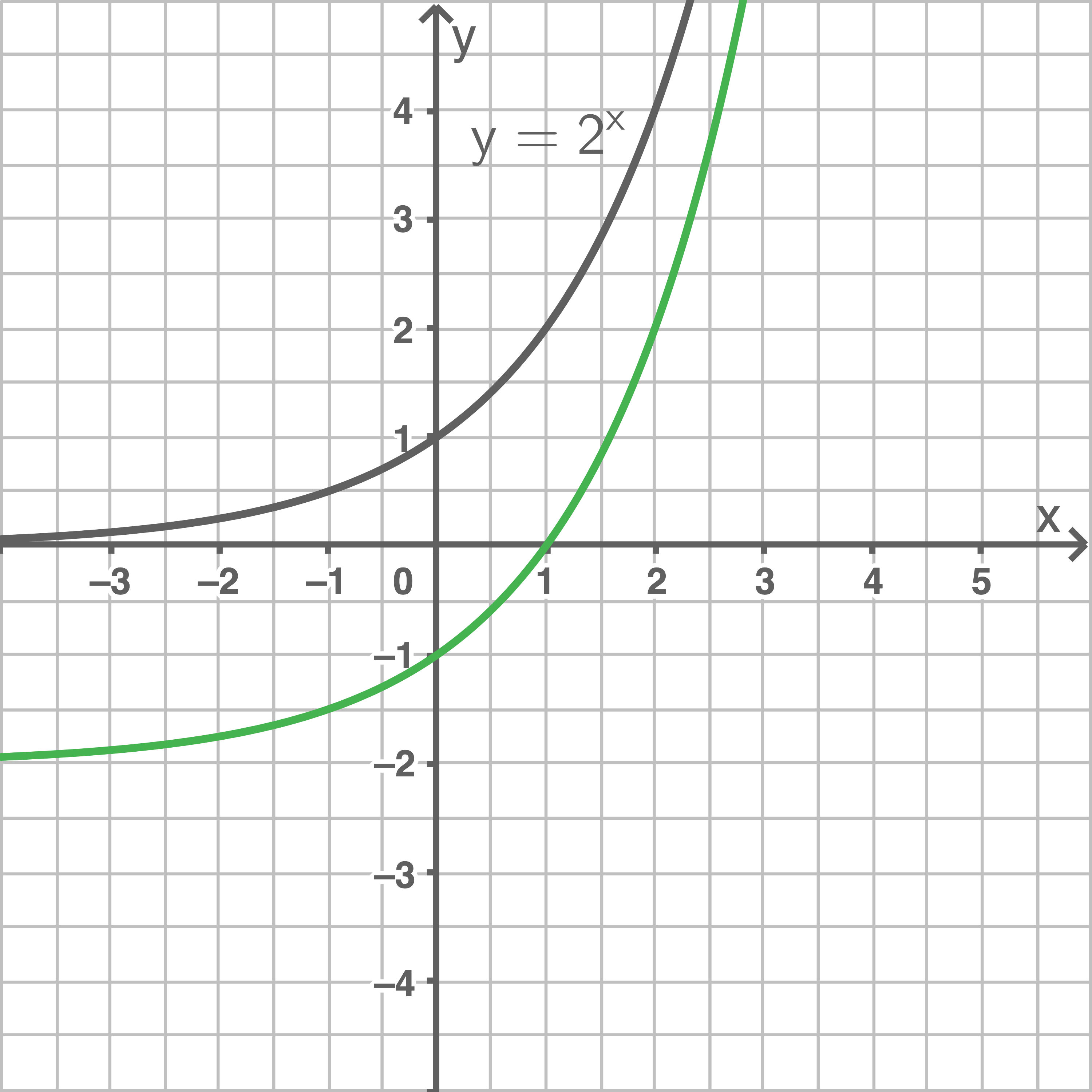
d)
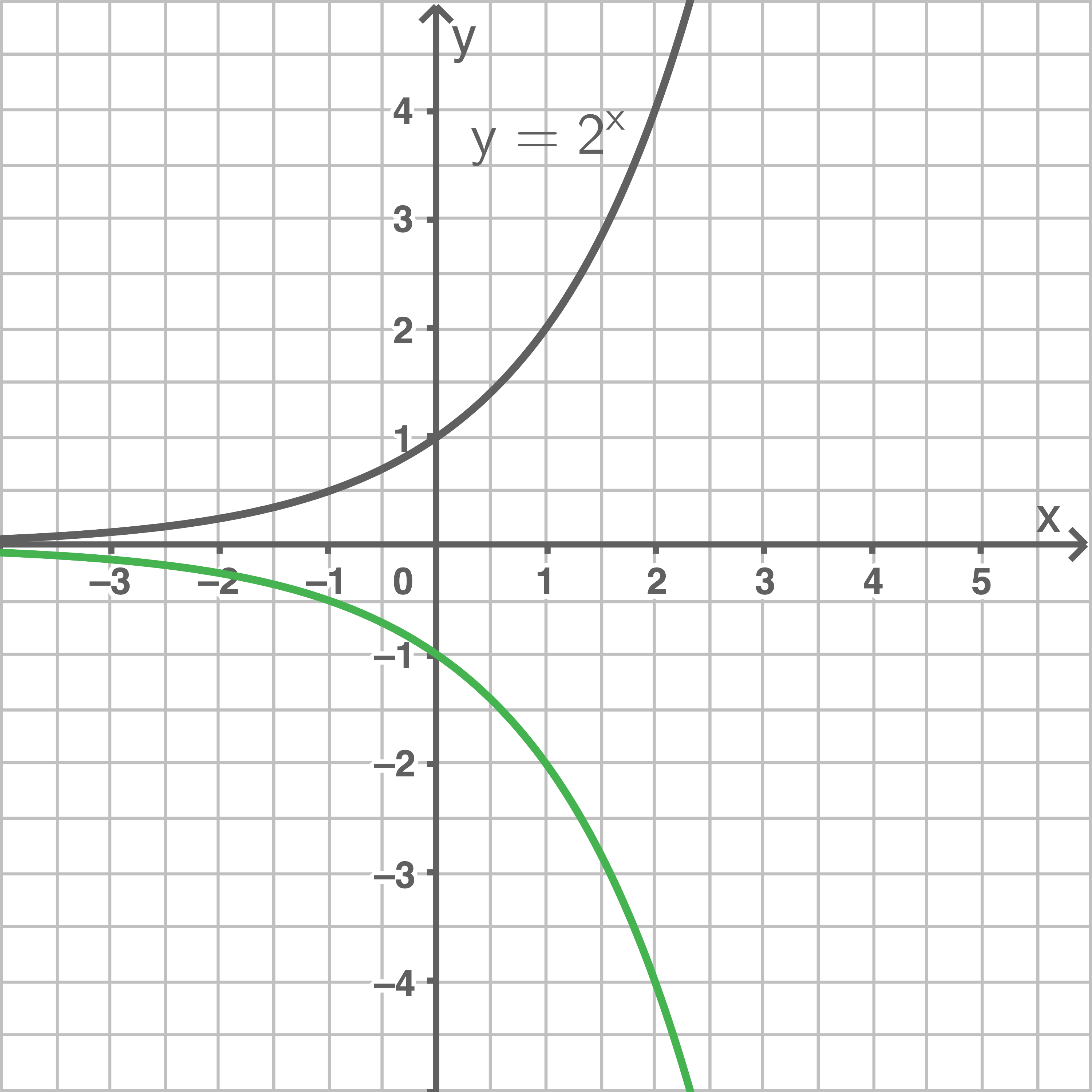
2
a)
b)
c)
d)