Logarithmusfunktion
Wird die Exponentialfunktion  umgekehrt, so entsteht die Logarithmusfunktion
umgekehrt, so entsteht die Logarithmusfunktion  Als Logarithmusfunktion zur Basis
Als Logarithmusfunktion zur Basis  wird die Funktion mit der Gleichung
wird die Funktion mit der Gleichung  (mit
(mit  bezeichnet.
Die Logarithmusfunktion zur Basis
bezeichnet.
Die Logarithmusfunktion zur Basis  hat die Gleichung
hat die Gleichung  und wird natürliche Logarithmusfunktion genannt.
Es gelten dabei folgende Eigenschaften:
und wird natürliche Logarithmusfunktion genannt.
Es gelten dabei folgende Eigenschaften:
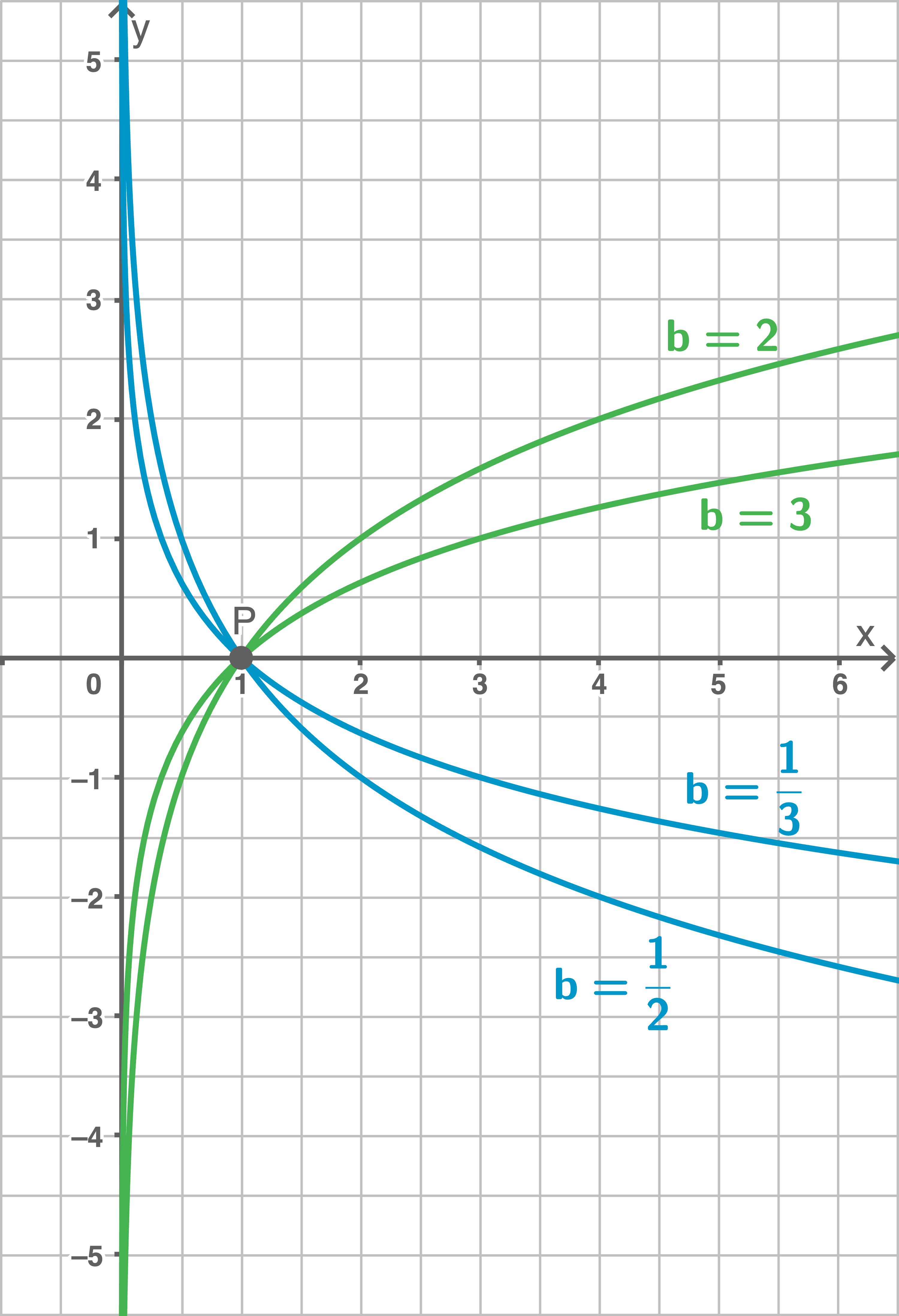
- Der Graph der Funktion
- steigt, wenn
- fällt, wenn
- Der Graph der Funktion verläuft rechts von der
-Achse. Für den Wertebereich gilt
- Für den Verlauf des Graphen gilt
- für
Verlauf unterhalb der
-Achse bis
danach oberhalb;
- für
Verlauf oberhalb der
-Achse bis
danach unterhalb.
- Der Graph nähert sich links der
-Achse an.
- Alle Graphen haben genau einen gemeinsamen Punkt und zwar
- Wird
mit einem Faktor
multipliziert, also
so kann stattdessen
geschrieben werden.

1
Zeichne den Graphen der gegebenen Logarithmusfunktion und nenne Eigenschaften des entsprechenden Graphen.




a)
b)
c)
d)
2
Gegeben ist der Punkt  durch den der Graph der Logarithmusfunktion mit
durch den der Graph der Logarithmusfunktion mit  verläuft. Bestimme die entsprechende Logarithmusfunktion.
verläuft. Bestimme die entsprechende Logarithmusfunktion.




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
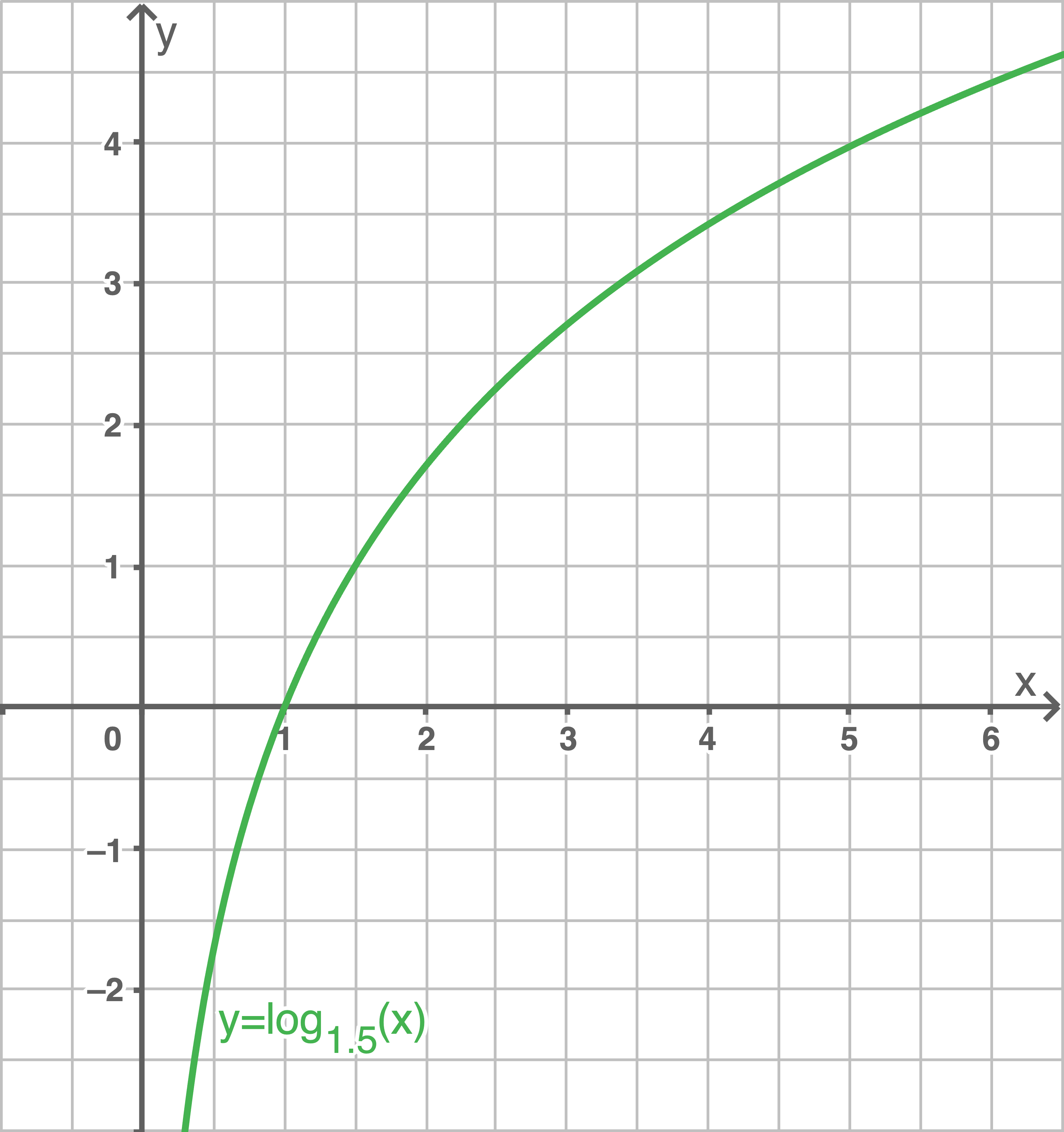
- Graph verläuft für
unterhalb der
-Achse.
- Graph verläuft für
oberhalb der
-Achse.
- Graph ist steigend, da
- Graph schneidet die
-Achse im Punkt
b)
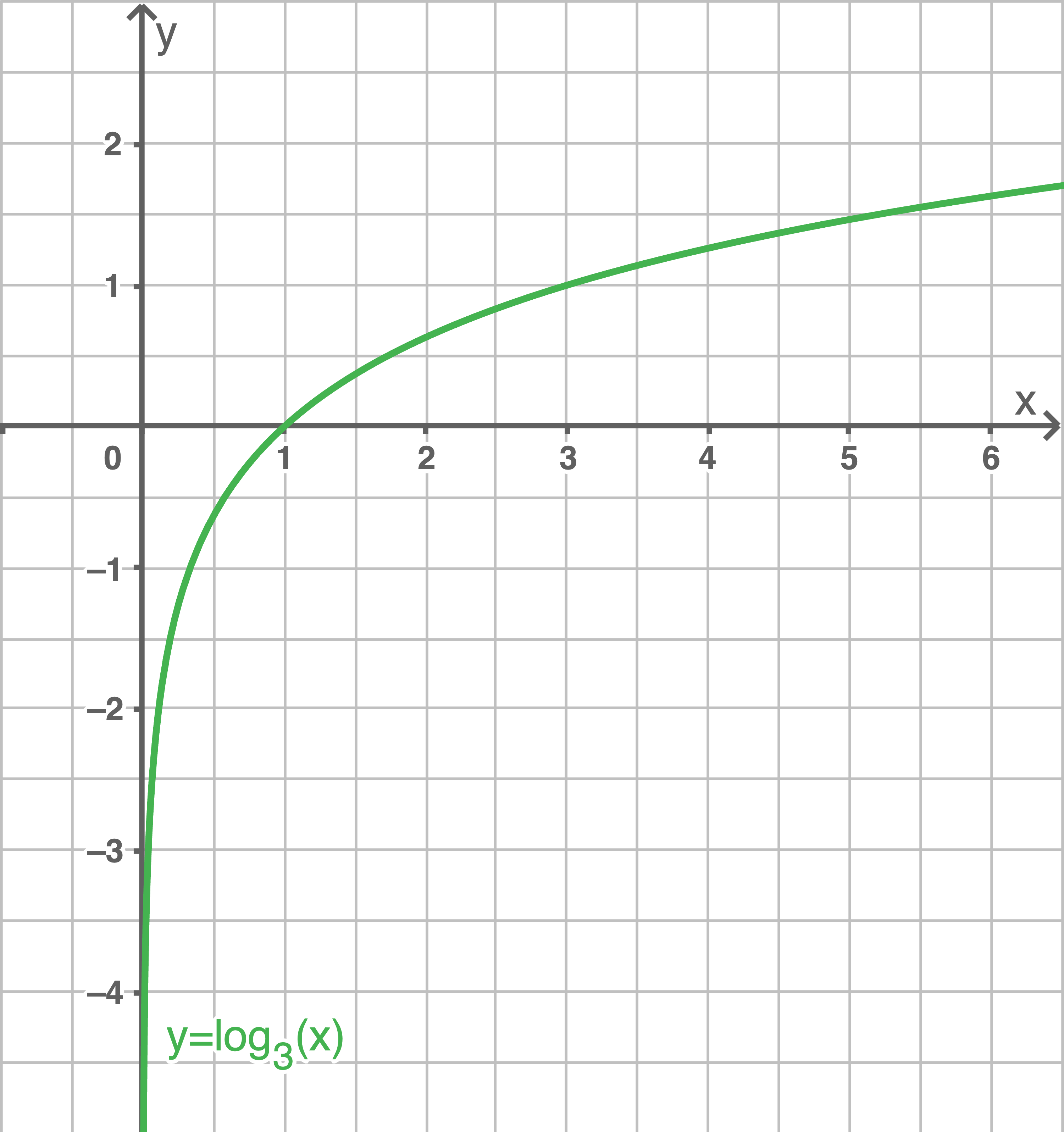
- Graph verläuft für
unterhalb der
-Achse.
- Graph verläuft für
oberhalb der
-Achse.
- Graph ist steigend, da
- Graph schneidet die
-Achse im Punkt
c)
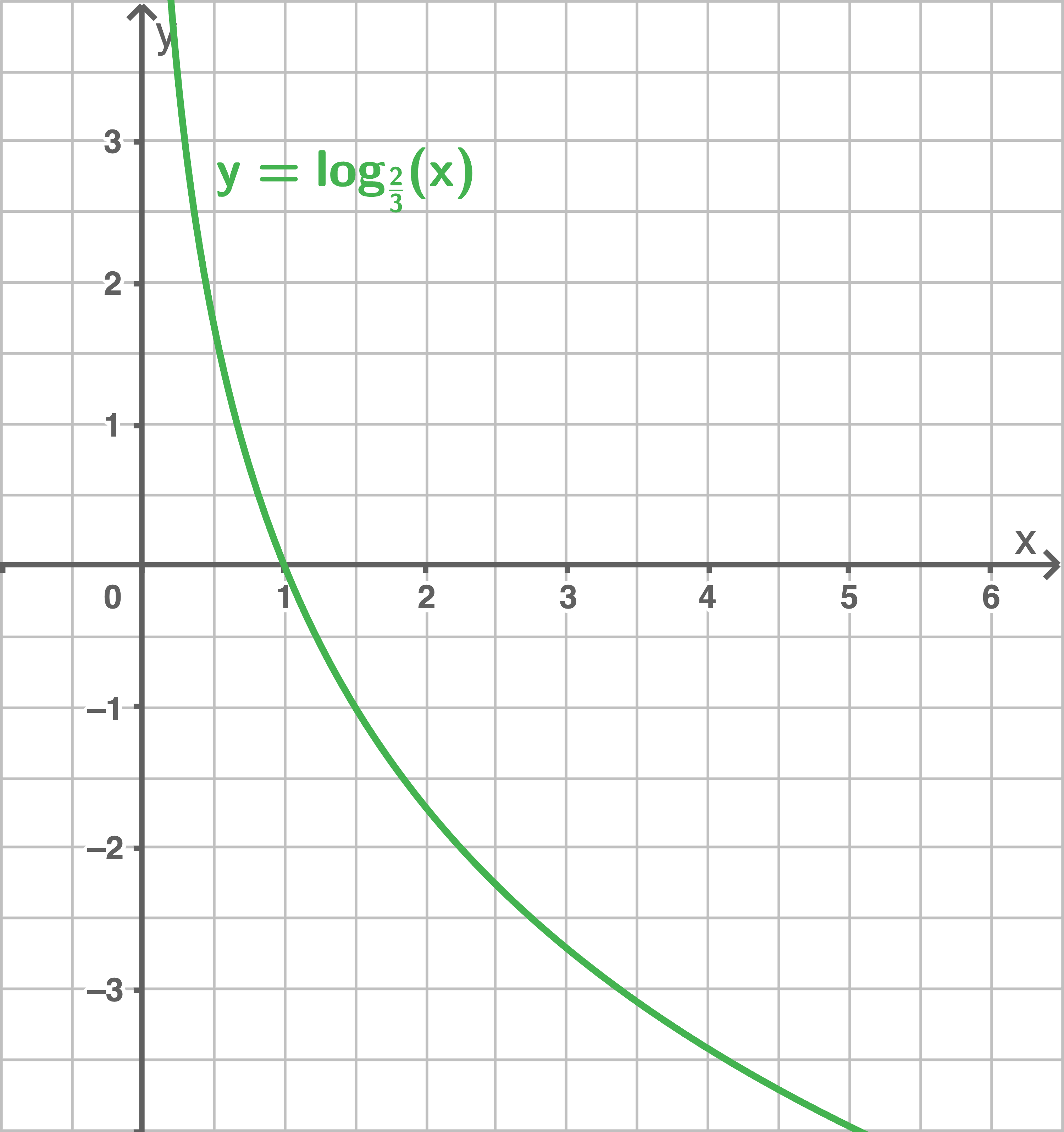
- Graph verläuft für
oberhalb der
-Achse.
- Graph verläuft für
unterhalb der
-Achse.
- Graph ist fallend, da
- Graph schneidet die
-Achse im Punkt
d)
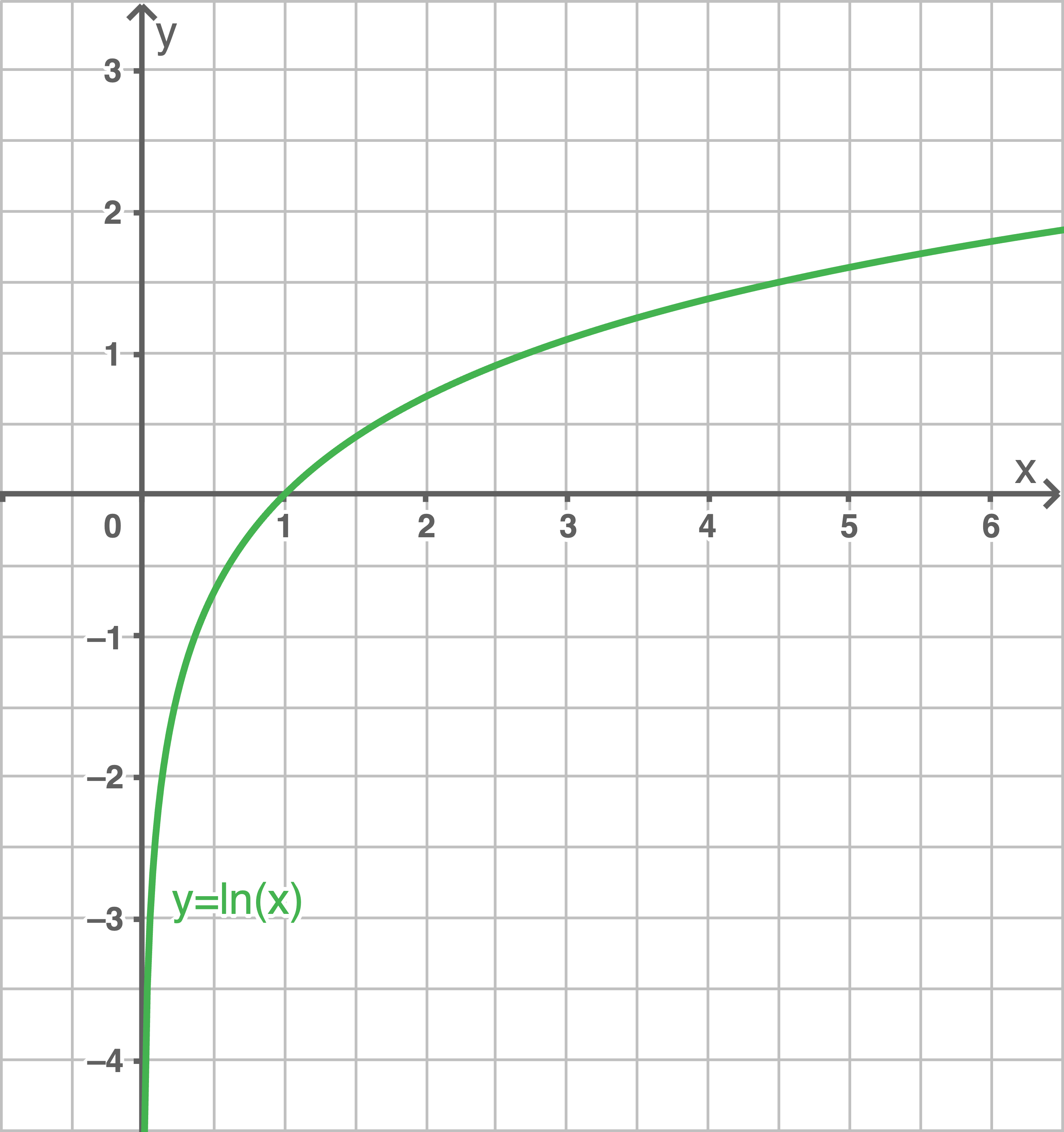
- Graph verläuft für
unterhalb der
-Achse.
- Graph verläuft für
oberhalb der
-Achse.
- Graph ist steigend, da
- Graph schneidet die
-Achse im Punkt
- Natürliche Logarithmusfunktion, da Basis
2
a)
b)
c)
d)