Verknüpfen von Funktionen
Addieren und Subtrahieren von Funktionen
Die FunktionMultiplizieren von Funktionen
Die FunktionDividieren von Funktionen
Die FunktionBeispiel
Die Funktion
1
Die Funktionen  und
und  mit
mit  und
und  sind im folgenden Koordinatensystem eingezeichnet.
sind im folgenden Koordinatensystem eingezeichnet.
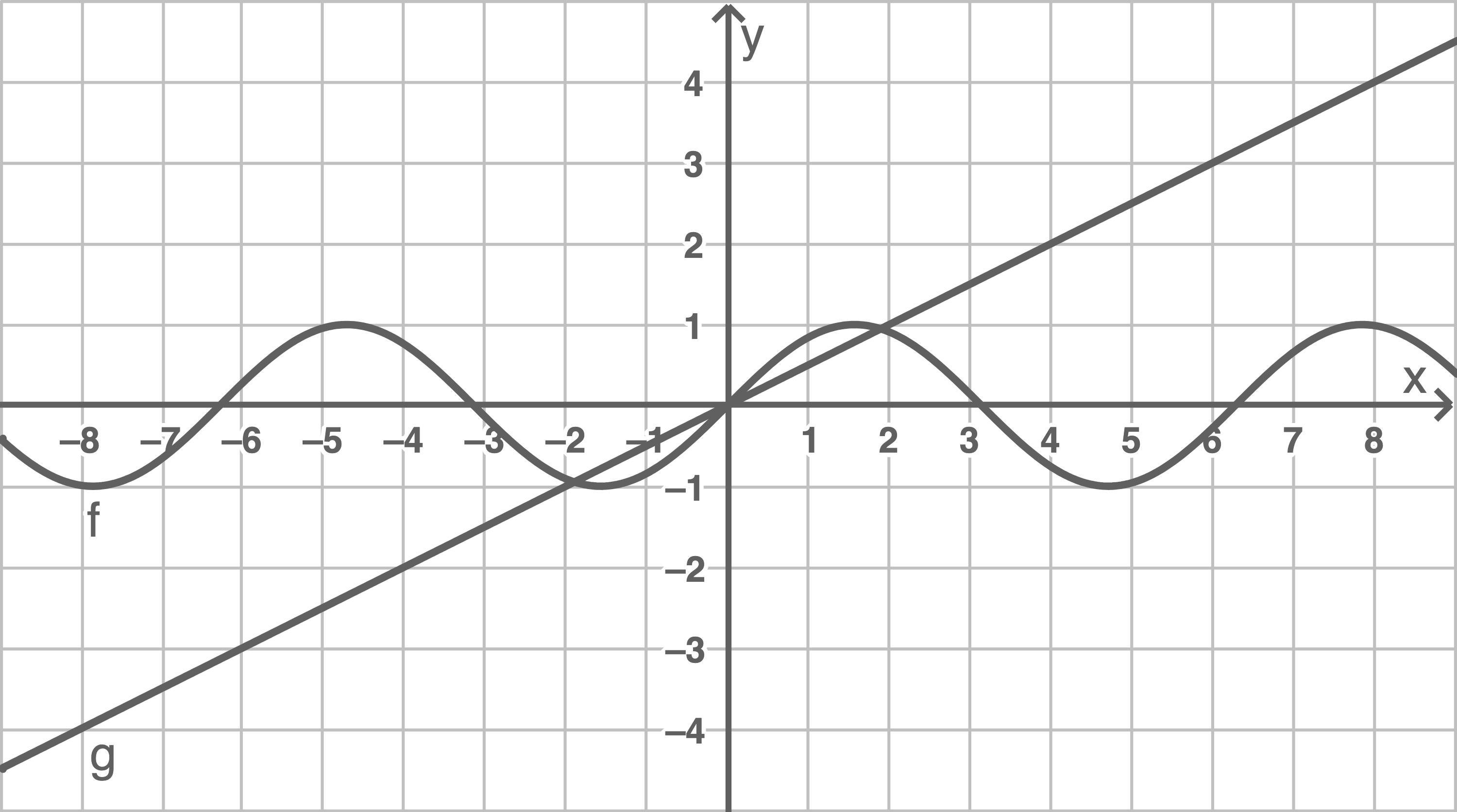 Gib jeweils die Funktion
Gib jeweils die Funktion  an, die durch die angegebene Verknüpfung der beiden Funktionen entsteht, und zeichne den Graphen in das Koordinatensystem ein.
an, die durch die angegebene Verknüpfung der beiden Funktionen entsteht, und zeichne den Graphen in das Koordinatensystem ein.

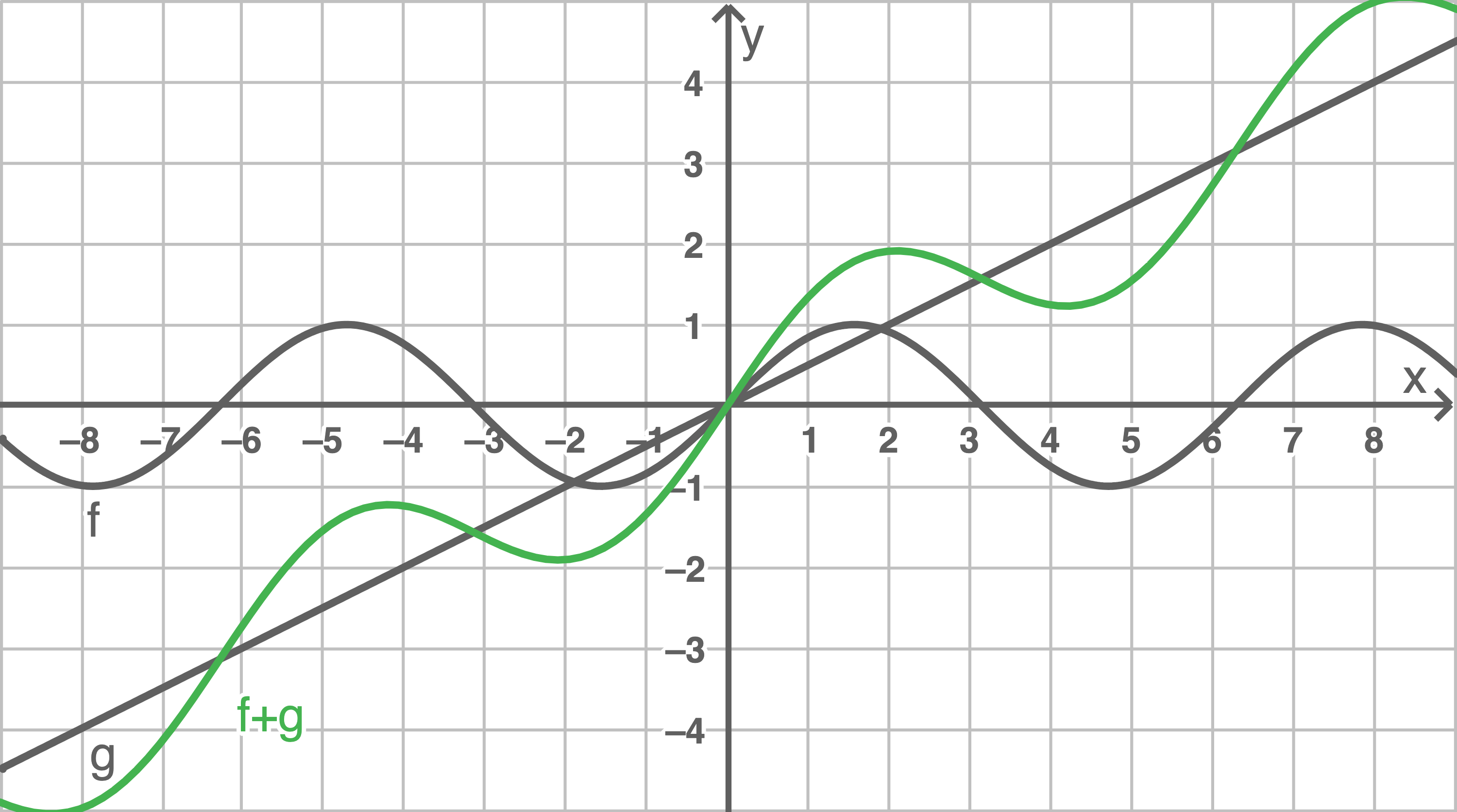
a)
Addition: 
b)
Subtraktion: 
c)
Multiplikation: 
d)
Division: 
2
Skizziere den Graphen der Funktion 




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
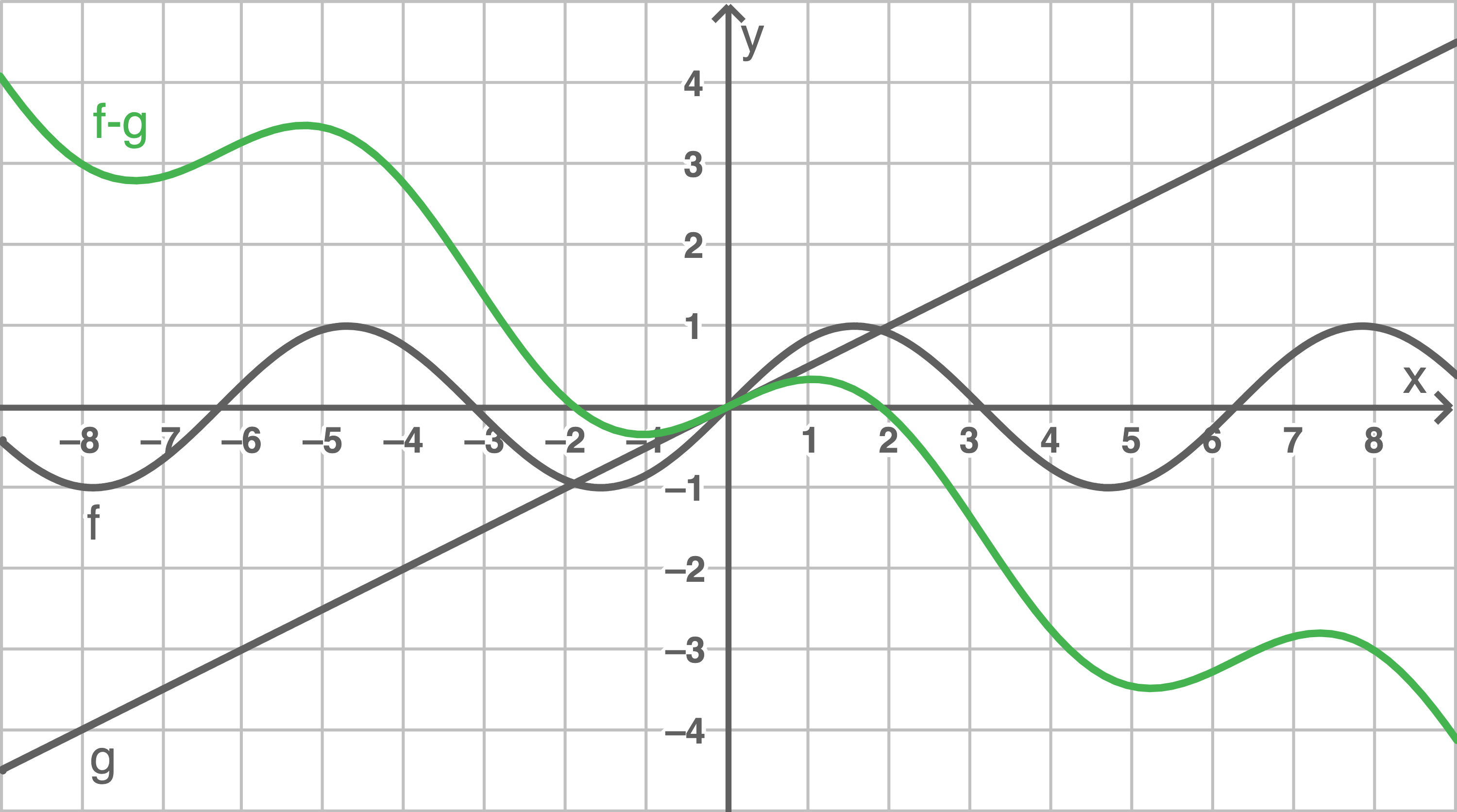
c)
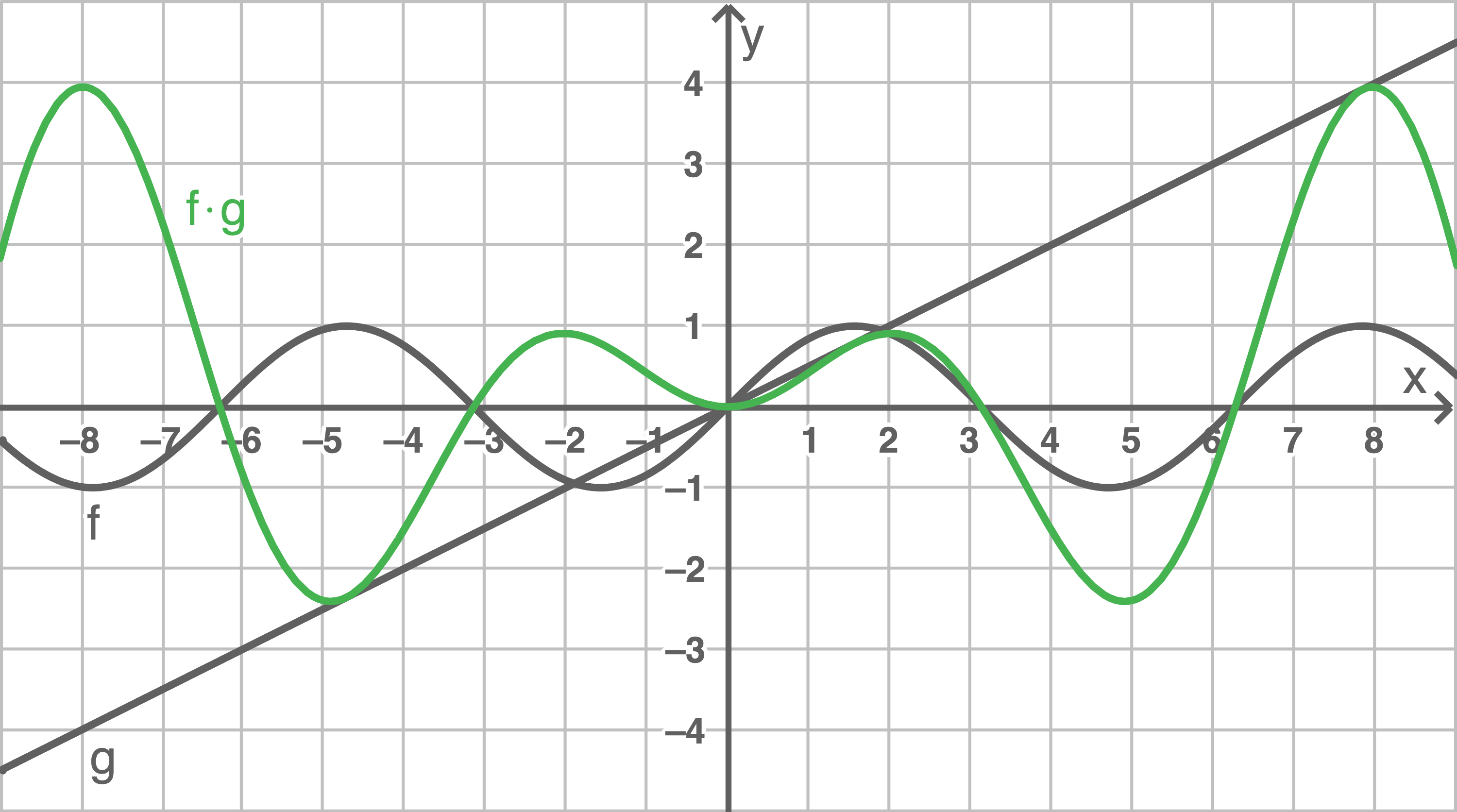
d)
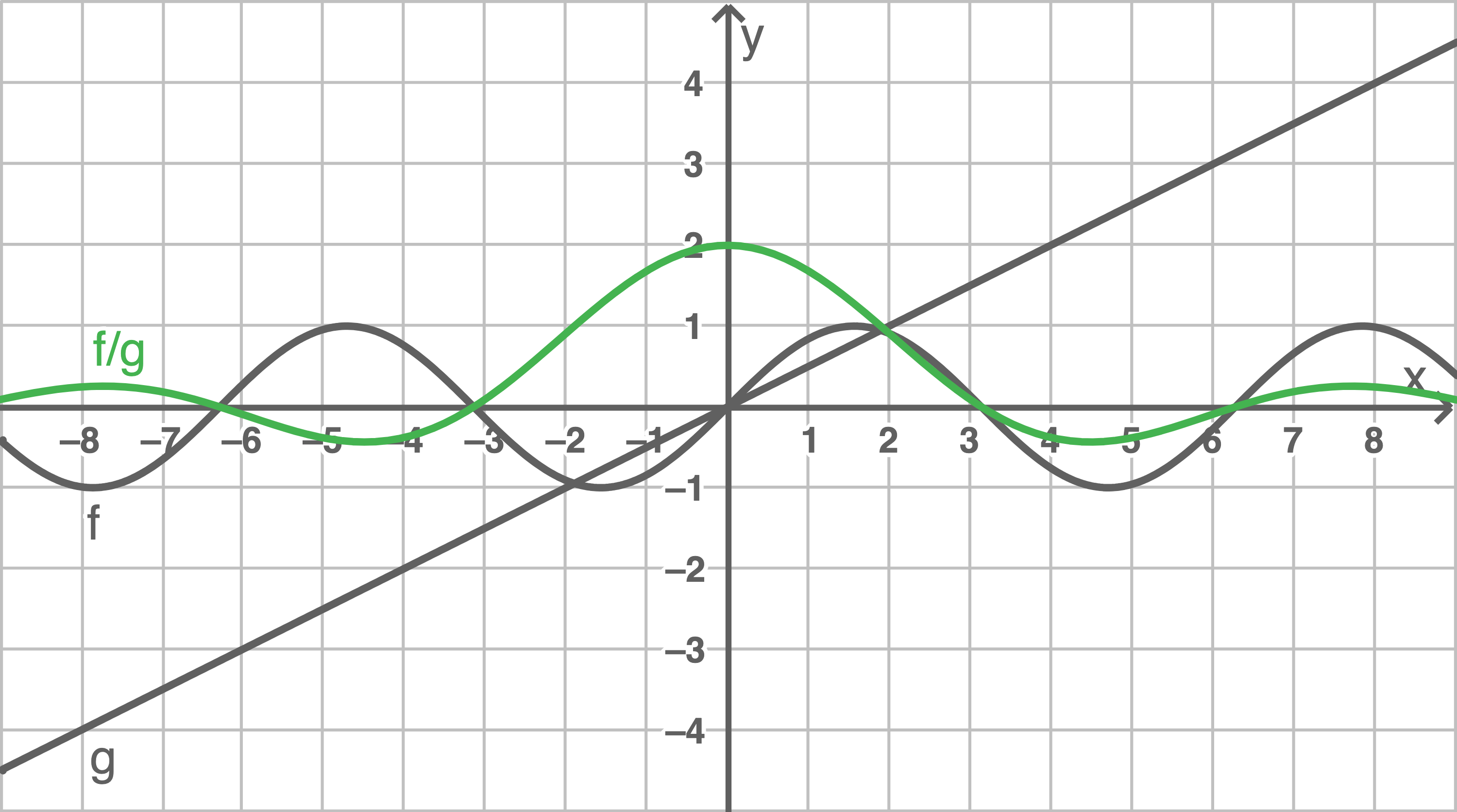
2
a)
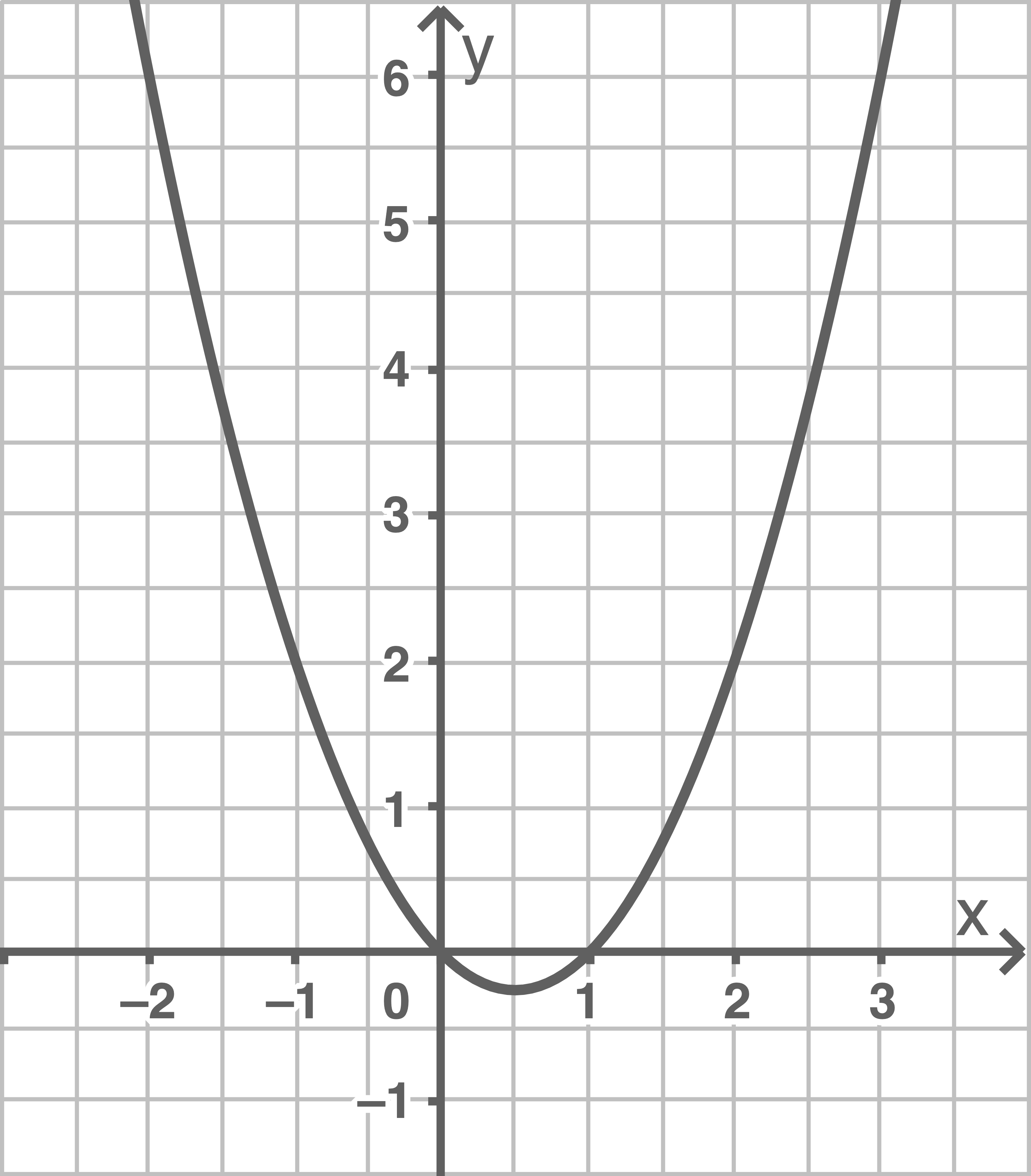
b)
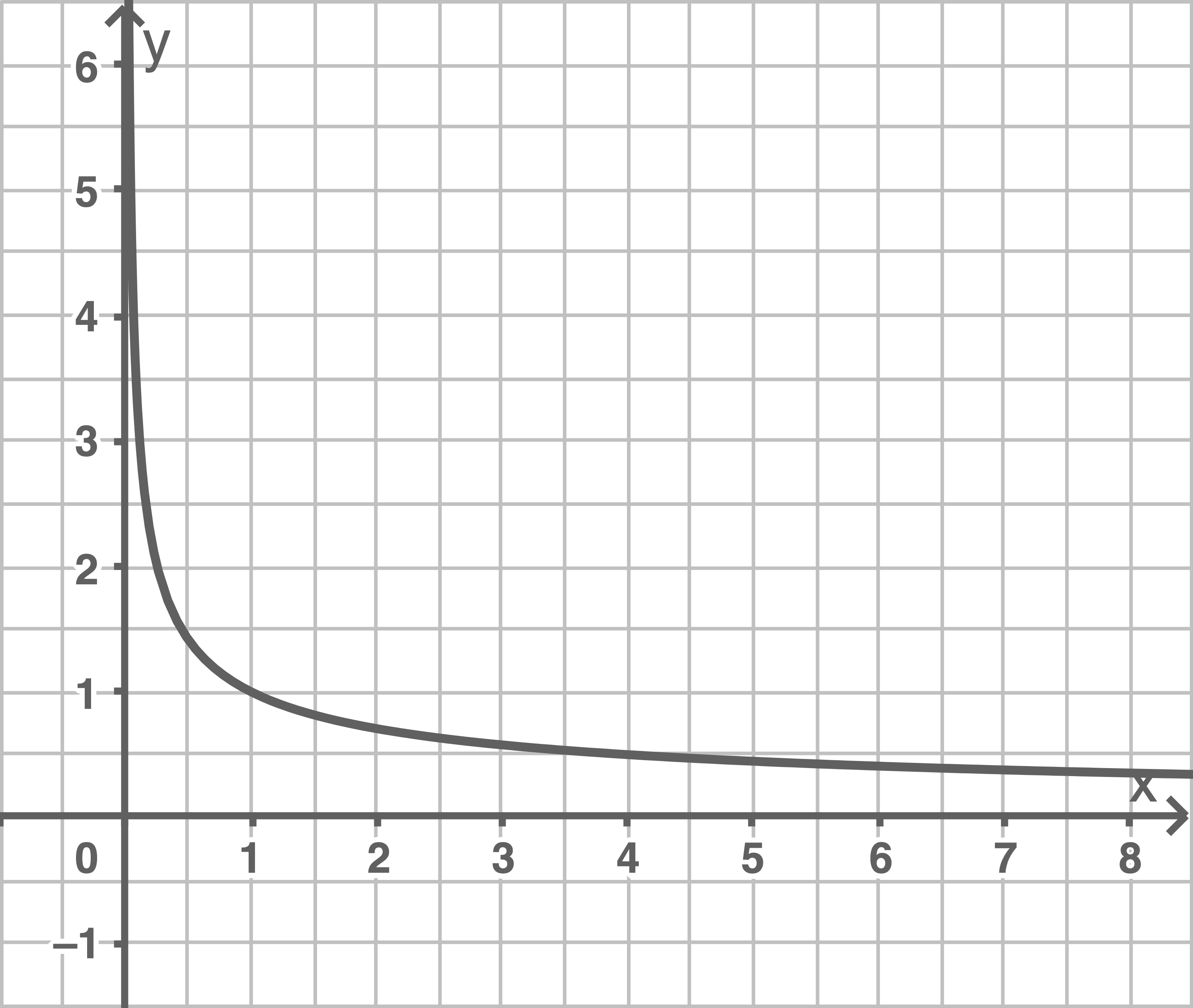
c)
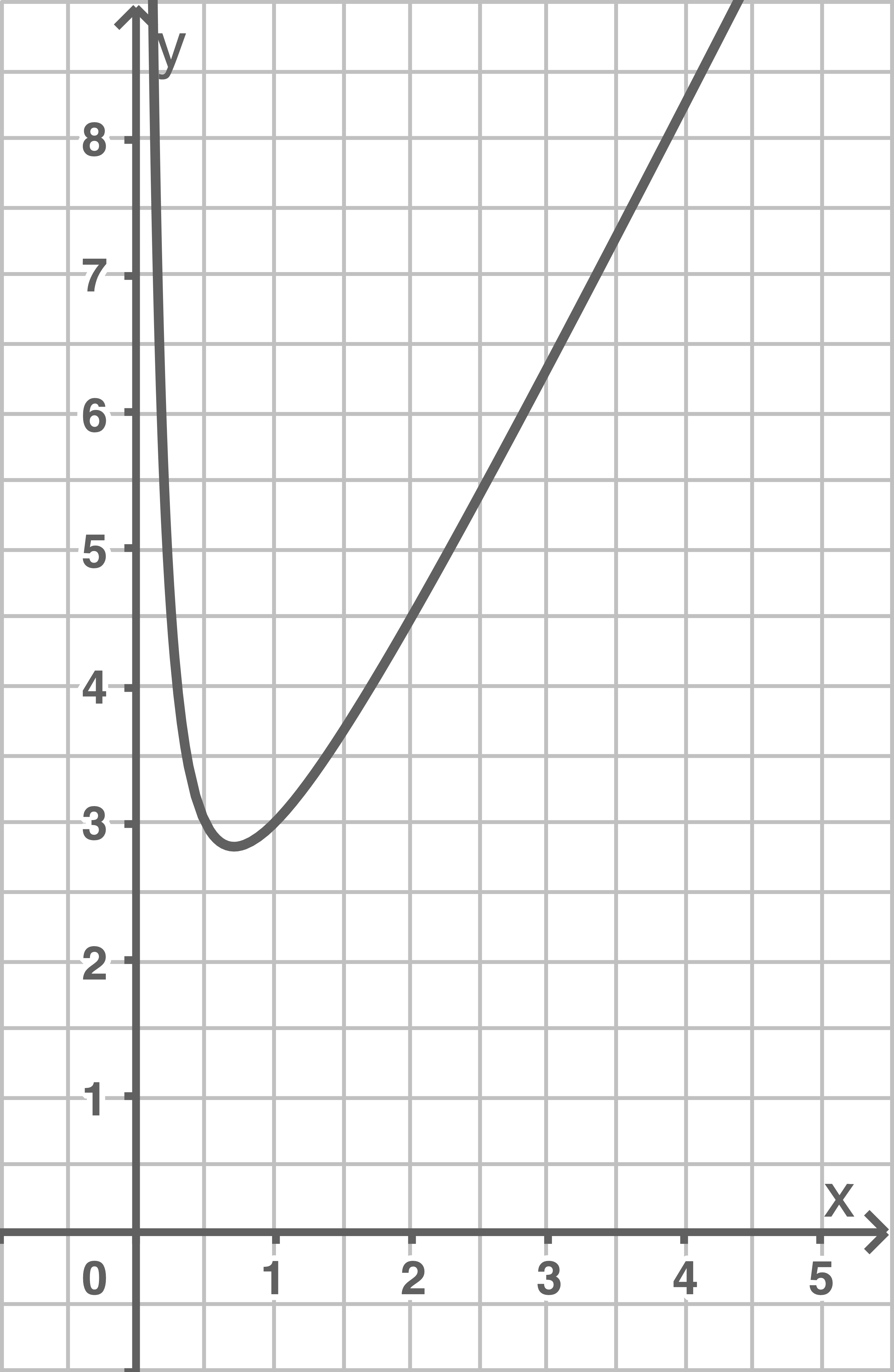
d)