Grafisches Lösungsverfahren linearer Gleichungssysteme
Wenn zwei lineare Gleichungen mit zwei Variablen durch "und" verknüpft werden, entsteht ein lineares Gleichungssystem (LGS). Jedes Zahlenpaar, das beide Gleichungen des Systems erfüllt, ist eine Lösung dieses LGS.
Verfahren zum grafischen Lösen eines LGS
- Beide Gleichungen so umformen, dass die zugehörigen Graphen gezeichnet werden können.
- Graphen in ein gemeinsames Koordinatensystem einzeichnen.
- Die Koordinatenpaare aller Punkte, die auf beiden Graphen liegen, sind Lösungen des LGS.
Lösungsmengen von LGS
Für LGS mit zwei Variablen in beiden Gleichungen gibt es die folgenden drei Fälle:-
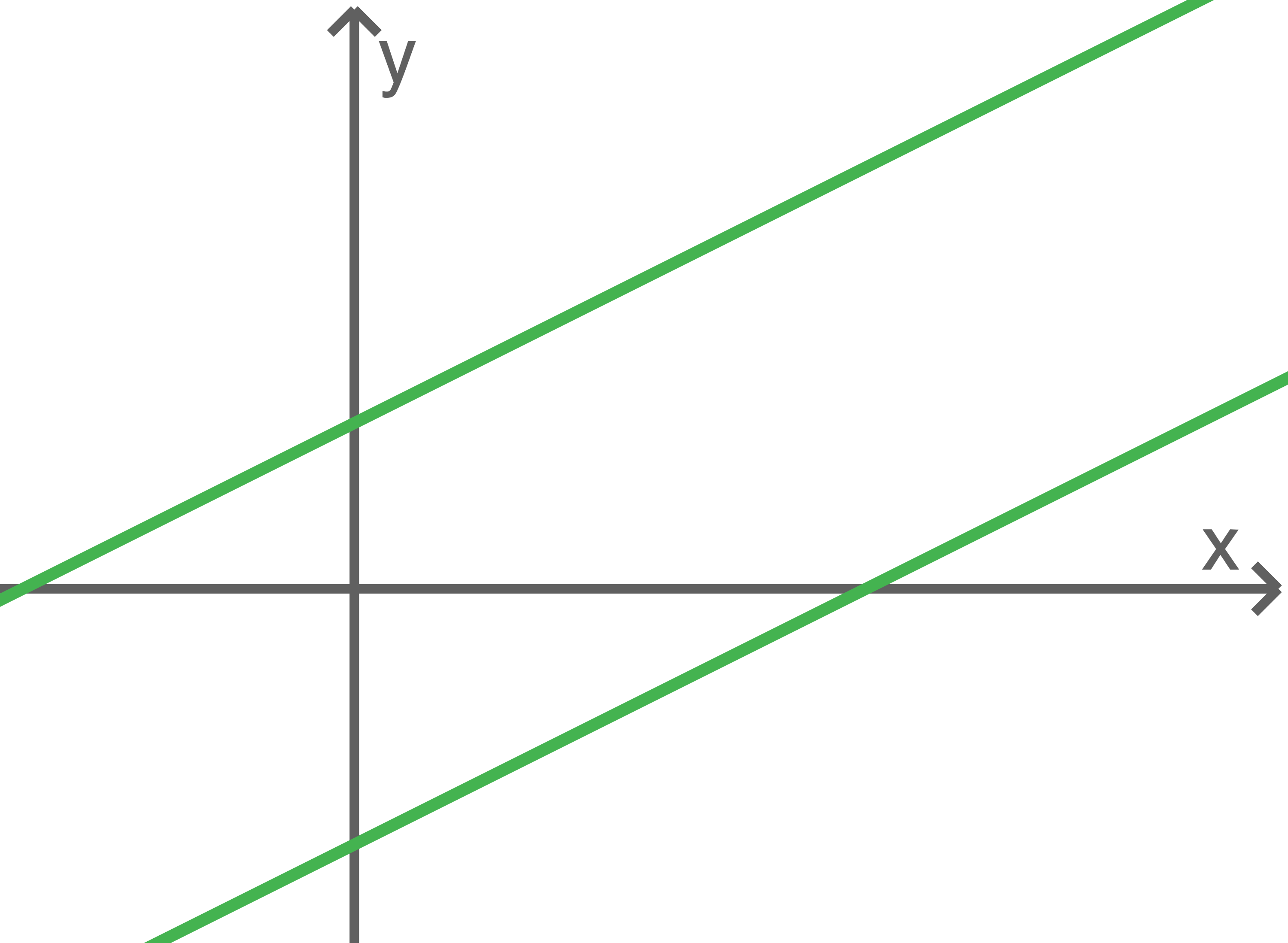
Das LGS hat keine Lösung, wenn beide Geraden die gleiche Steigung, aber einen unterschiedlichen
-Achsenabschnitt haben. Die Geraden verlaufen parallel und schneiden sich nicht, die Lösungsmenge ist also leer.
-
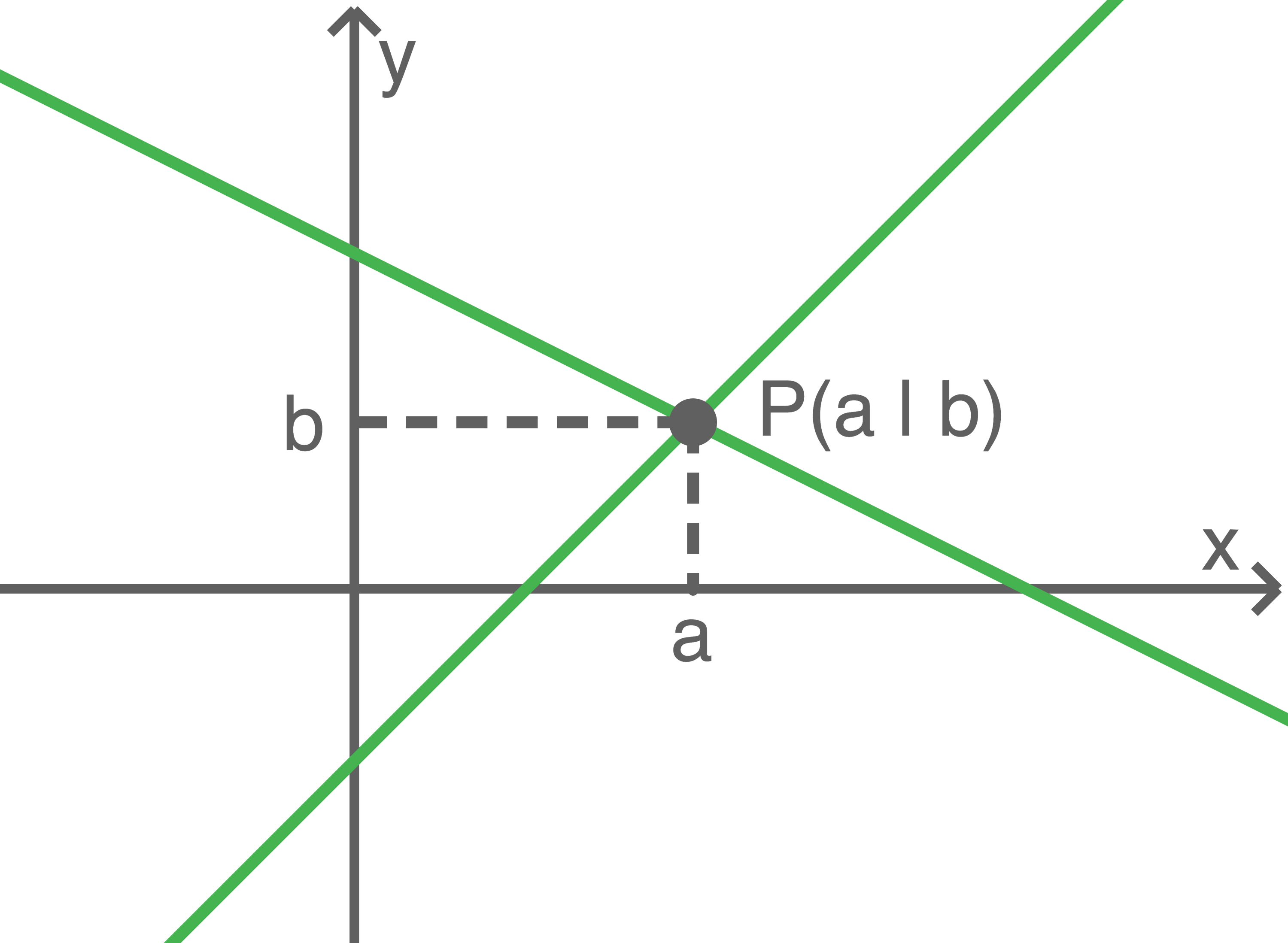
Das LGS hat genau eine Lösung, wenn beide Geraden unterschiedliche Steigungen haben. Die Lösungsmenge besteht aus dem Koordinatenpaar des einzigen Schnittpunkts.
-
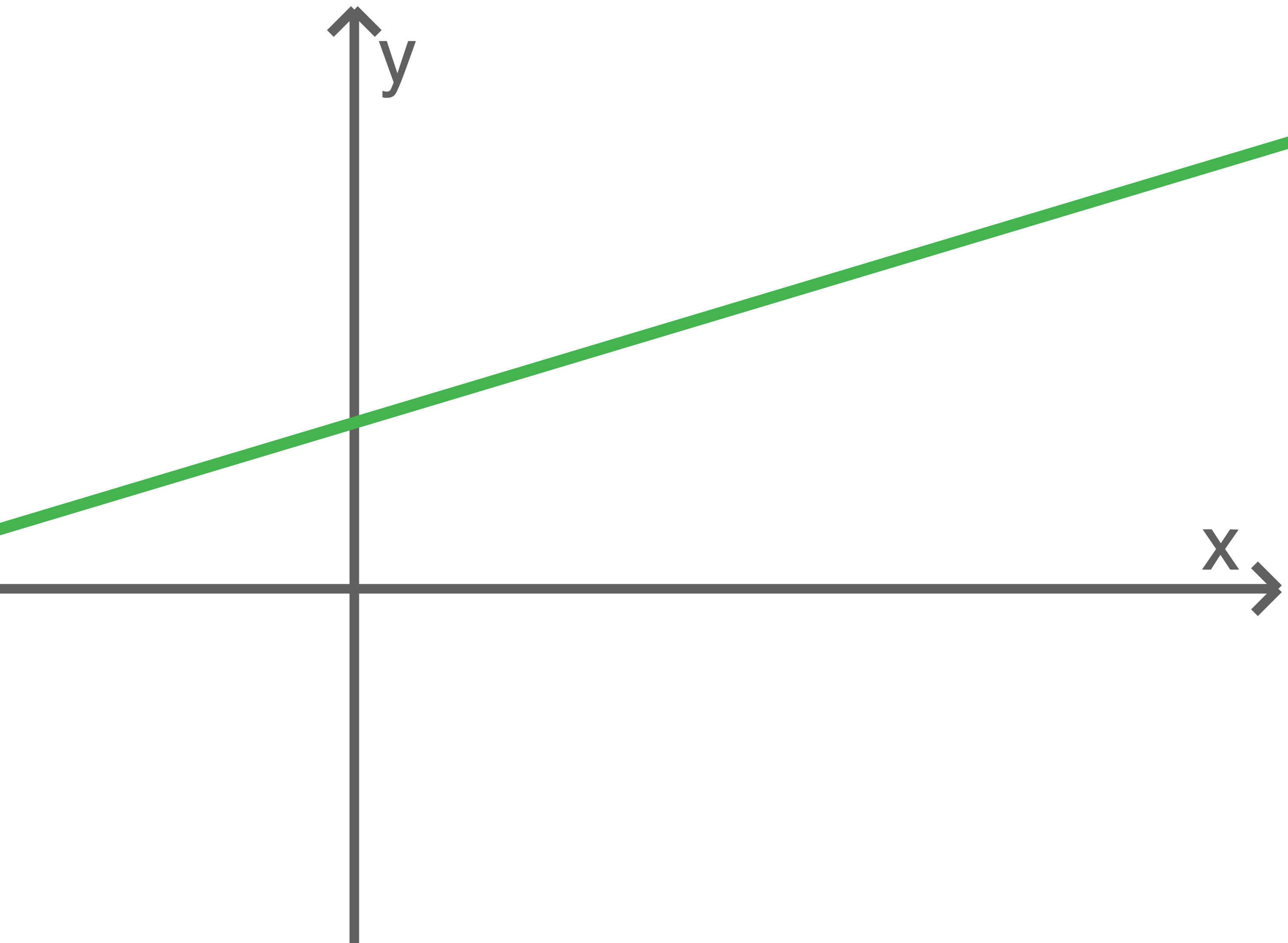
Das LGS hat unendlich viele Lösungen, wenn beide Geraden die gleiche Steigung und den gleichen
-Achsenabschnitt haben. Die Geraden sind identisch und die Lösungsmenge besteht aus allen Zahlenpaaren, die die Geradengleichung erfüllen.
1
Forme die Gleichungen geeignet um und gib an, wie viele Lösungen das LGS hat. Bestimme gegebenenfalls zeichnerisch die Lösungsmenge.
![\(\begin{array}[t]{|lrl|}
& 2x+3y &=& 7 & \\[5pt]
& 4x+2y&=& 10
\end{array}\)](https://mathjax.schullv.de/e5286bfc57187ca21b33572b109dc9f275de6990dae1f201fa6a63f764f3a78d?color=5a5a5a)
![\(\begin{array}[t]{|lrl|}
& -2x+4y &=& -2 & \\[5pt]
& 2x-4y&=& -2
\end{array}\)](https://mathjax.schullv.de/22a7701f4d0789d75505ed1c11562096a3600f842b299378e10ca6b481125d04?color=5a5a5a)
![\(\begin{array}[t]{|lrl|}
& 4x-2y &=& 8 & \\[5pt]
& 2x-y&=& 4
\end{array}\)](https://mathjax.schullv.de/607a39c23a861d8409cadf20eb44158907ad1ce6aaf6e4281aa04fc1d939728c?color=5a5a5a)
a)
b)
c)
2
Gib zur Gleichung  eine weitere Gleichung an, sodass das LGS
eine weitere Gleichung an, sodass das LGS
a)
keine Lösung hat.
b)
genau eine Lösung hat.
c)
unendlich viele Lösungen hat.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
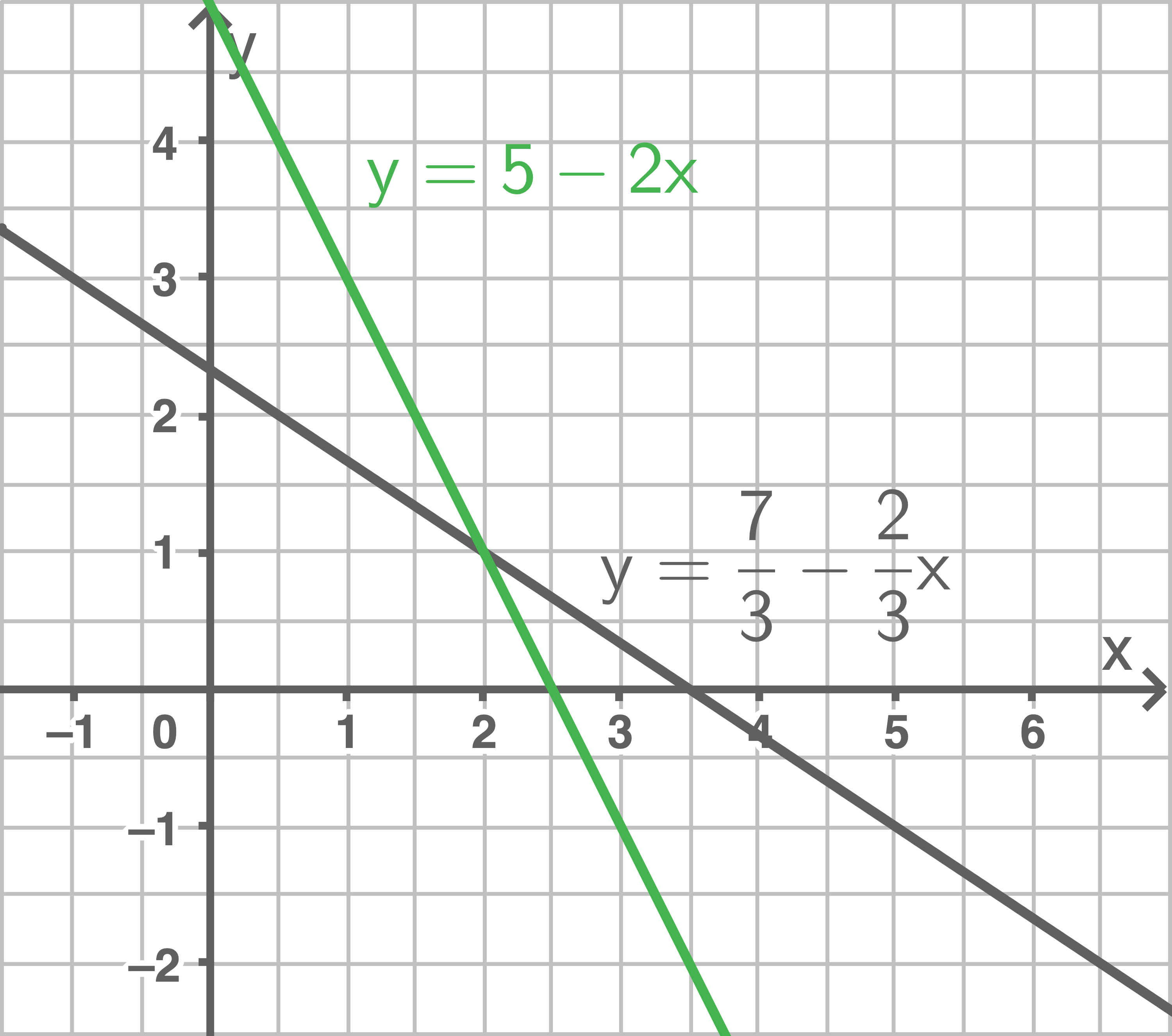
b)
c)
2
a)
b)
c)