Verschieben und Strecken der Graphen von Potenzfunktionen
Die allgemeine Potenzfunktion ist von der Form 
Der Graph einer Potenzfunktion ergibt sich, indem der Graph von 
nacheinander
Der Graph einer Potenzfunktion ergibt sich, indem der Graph von nacheinander
- um
Einheiten entlang der 
-Achse verschoben wird:
für
nach rechts und für 
nach links. - mit dem Faktor
entlang der 
-Achse gestreckt wird.
Für
wird der Graph an der 
-Achse gespiegelt. - um
Einheiten entlang der -Achse verschoben wird:
für
nach unten und für 
nach oben.
1
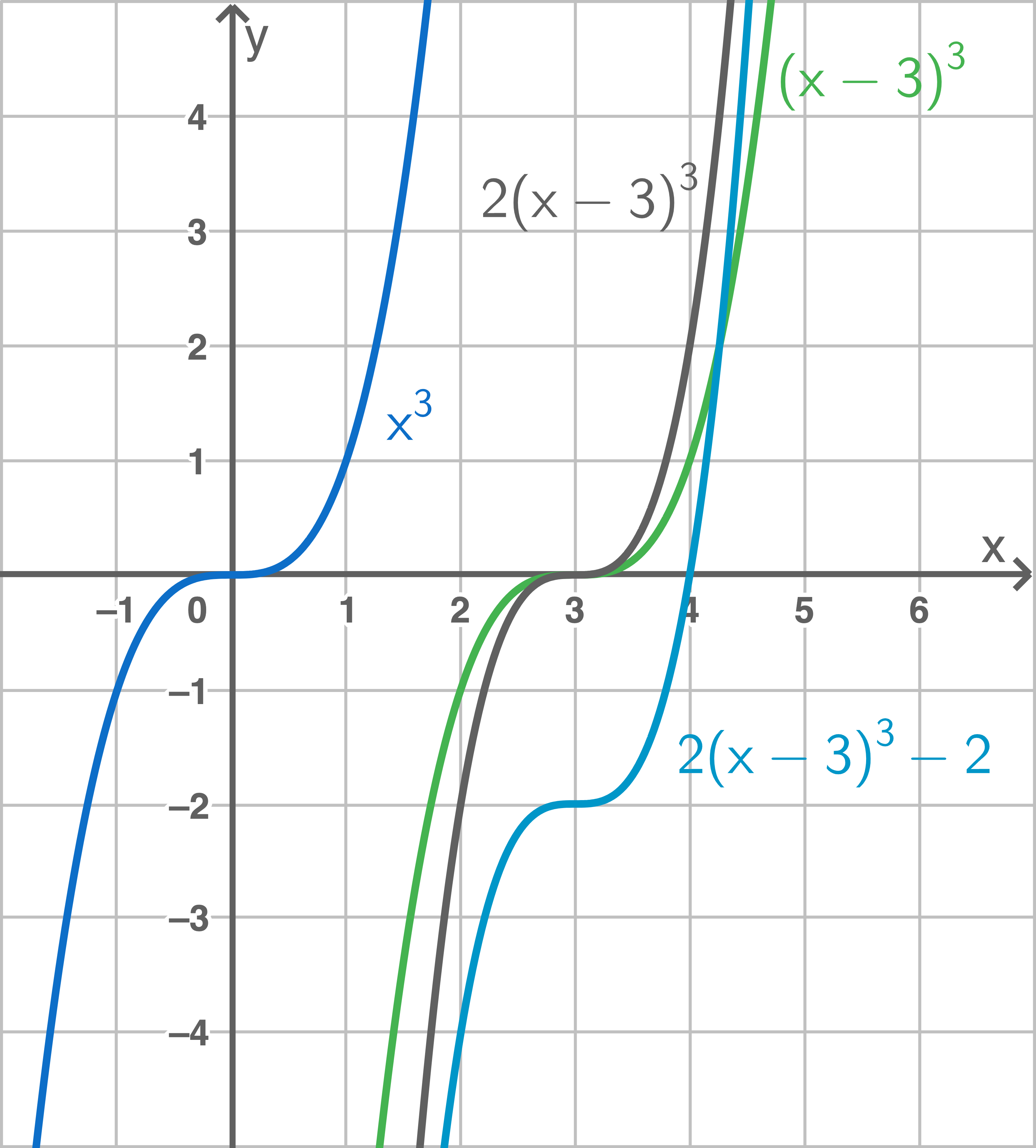
Zeichne den Graphen der Funktion und beschreibe, wie er aus den Graphen der Funktionen 
bzw. 
hervorgeht.
bzw. hervorgeht.
a)
b)
c)
d)
2
Bestimme die Funktionsgleichung.
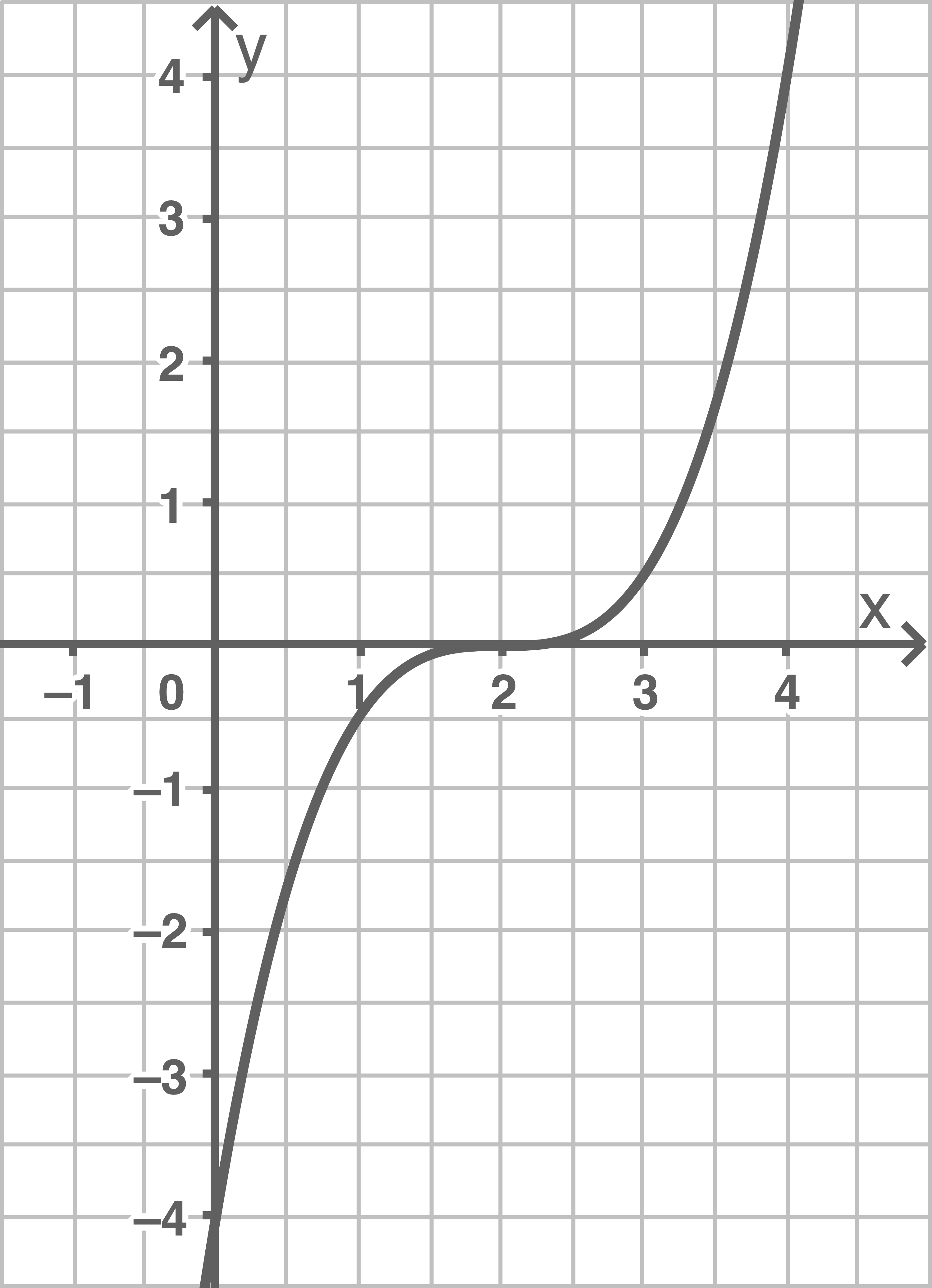
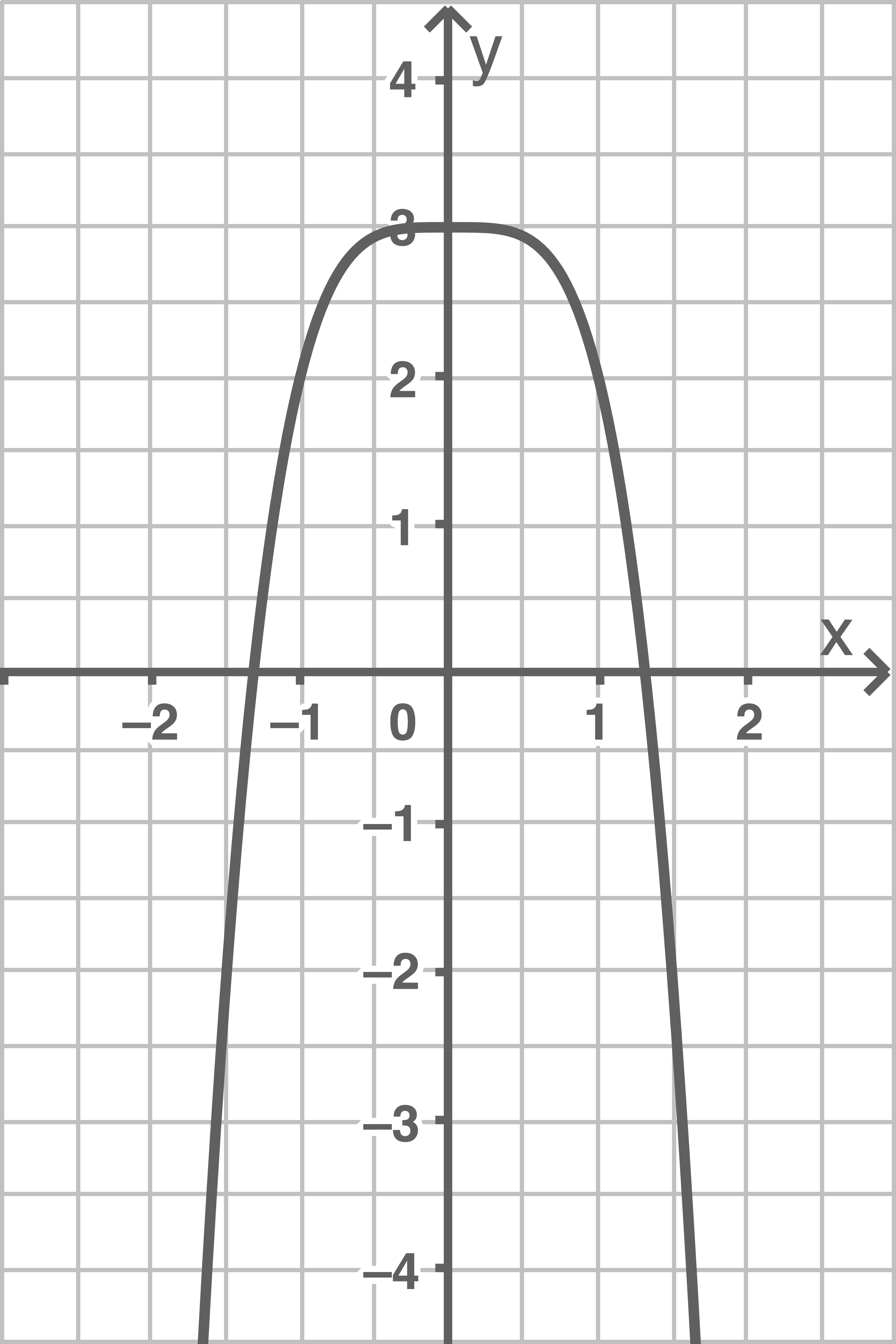
a)
Der Graph der Funktion wird um zwei Einheiten nach rechts und um eine Einheit nach oben verschoben.
wird um zwei Einheiten nach rechts und um eine Einheit nach oben verschoben.
b)
Der Graph der Funktion wird um eine Einheit nach links verschoben, an der -Achse gespiegelt und um vier Einheiten nach oben verschoben
wird um eine Einheit nach links verschoben, an der -Achse gespiegelt und um vier Einheiten nach oben verschoben
c)
d)
Weiter lernen mit SchulLV Plus!
monatlich kündbarSchulLV Plus-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
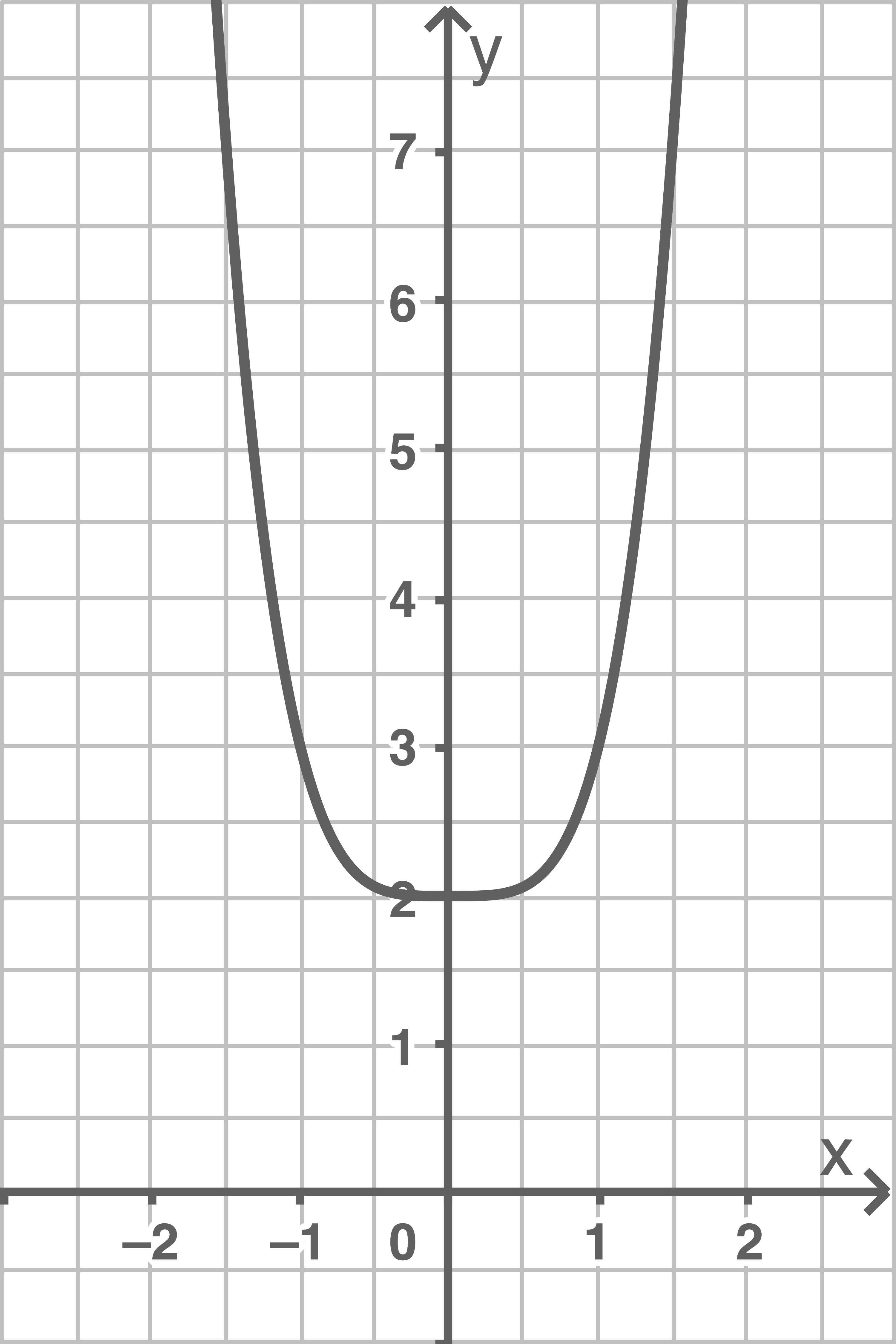
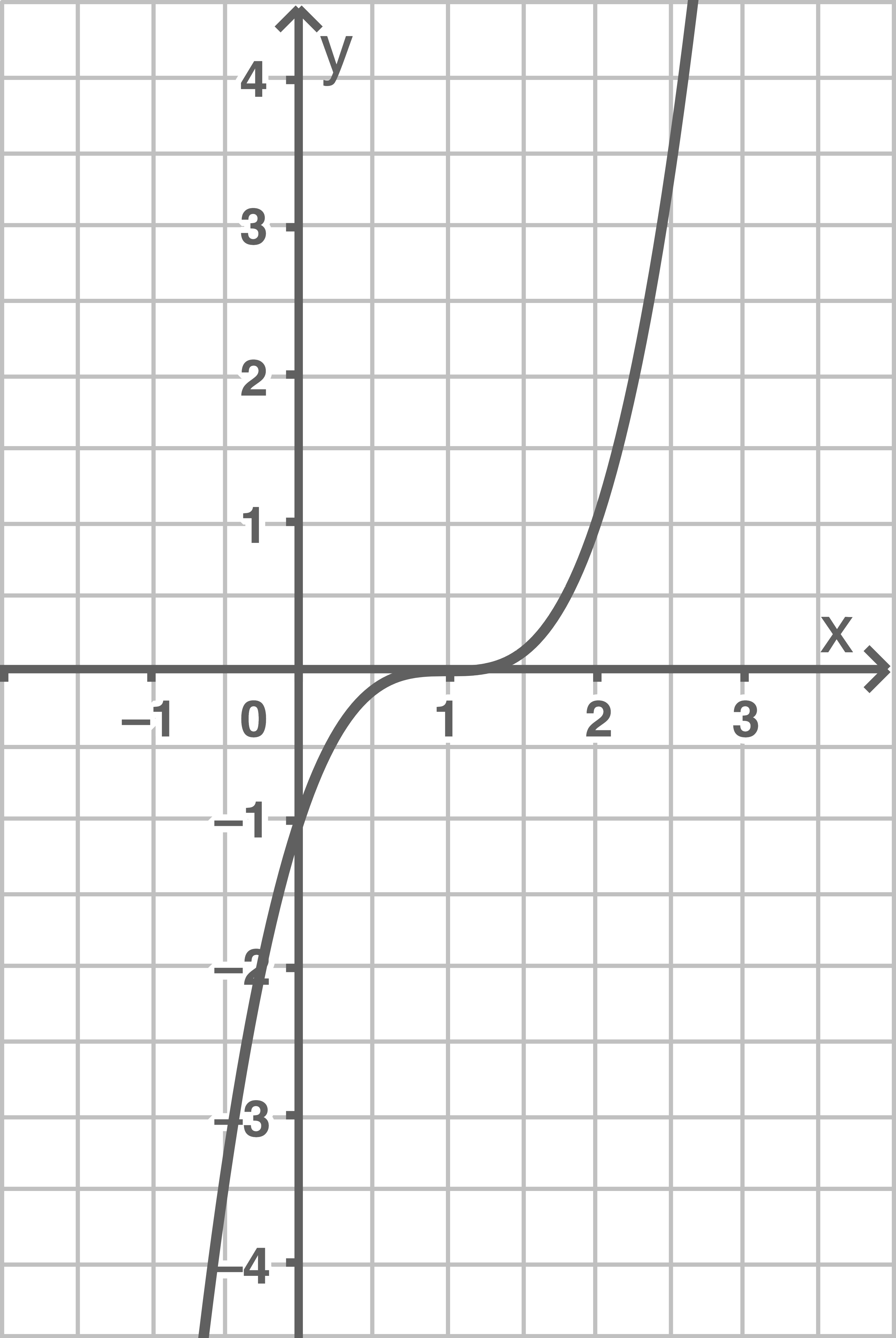
wird um zwei Einheiten nach oben verschoben.
b)
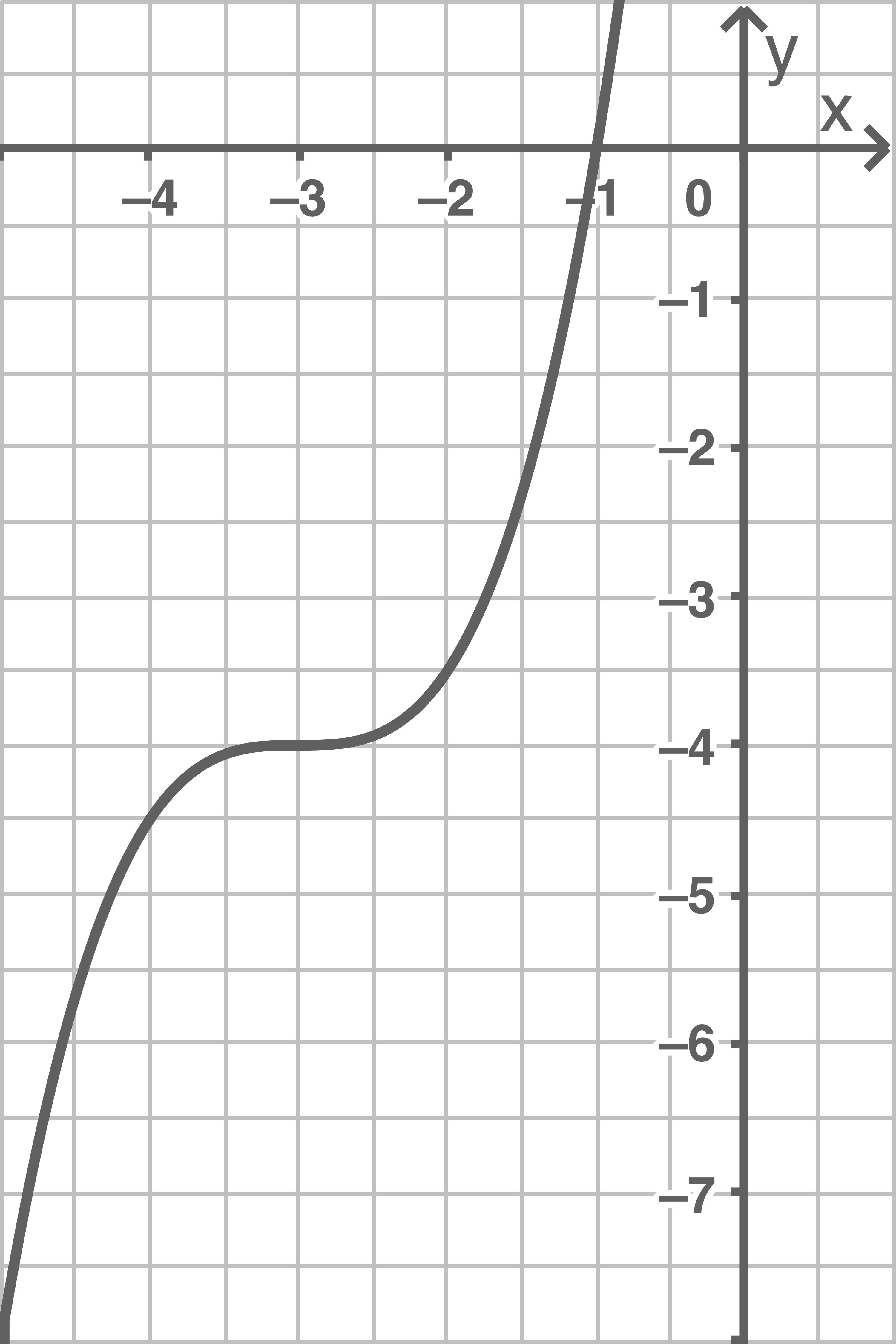
wird um eine Einheiten nach rechts verschoben.
c)
wird um drei Einheiten nach links verschoben, mit dem Faktor 
gestreckt und um vier Einheiten nach unten verschoben.
d)
wird um zwei Einheiten nach rechts verschoben, mit dem Faktor 
gestreckt und um eine Einheit nach oben verschoben.
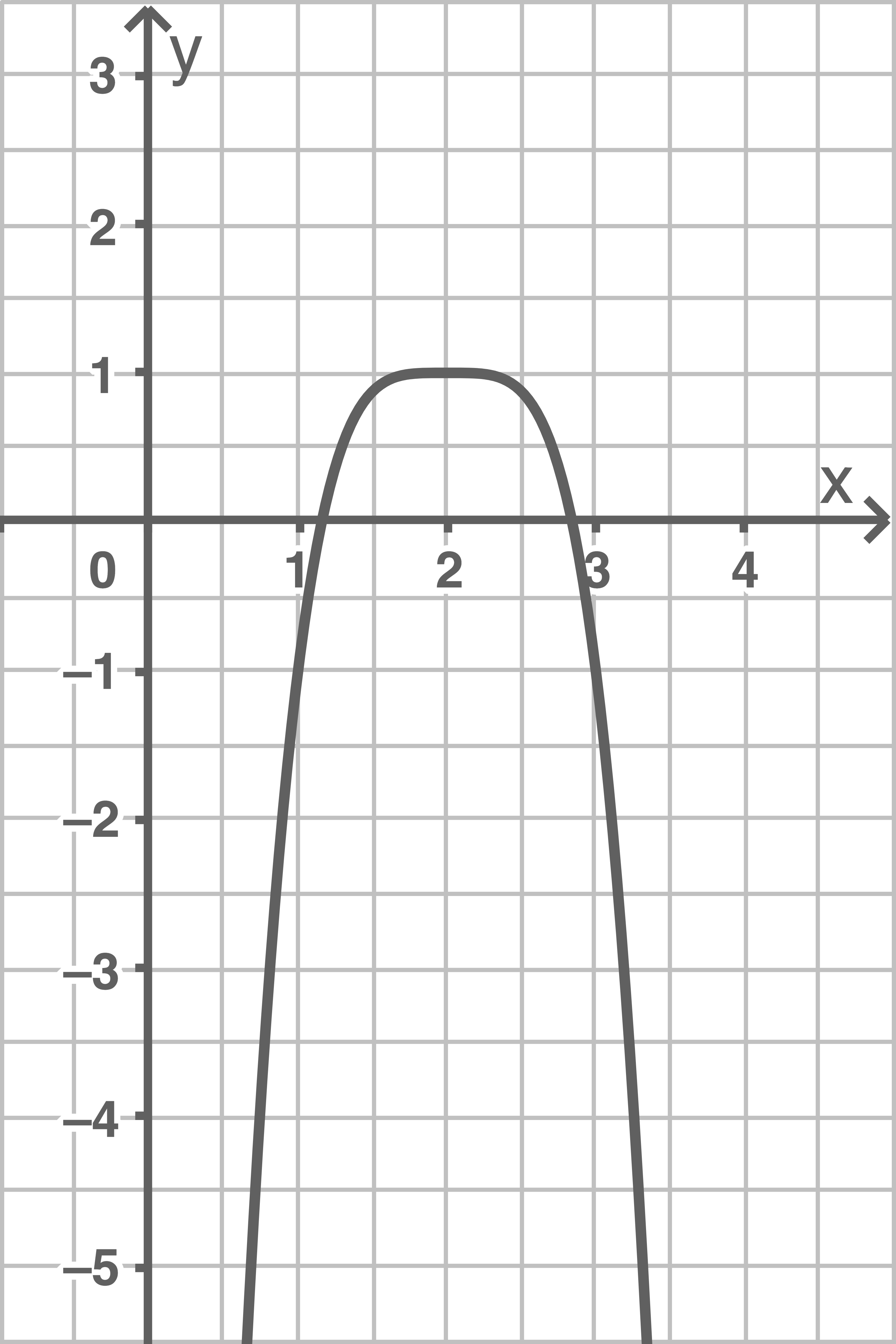
2
a)
b)
c)
d)
