Potenzen mit ganzzahligem Exponent

Wird eine Zahl mehrfach mit sich selbst multipliziert, lässt sich dieses Produkt auch übersichtlich mit der Potenzschreibweise darstellen.

Definition

Es gilt: $a^n=\underbrace{a\cdot a\cdot a\cdot a\cdot ...\cdot a}_{\text{n Faktoren}}\quad (n\in \mathbb{N}, n\geq 1)$
für jede reelle Zahl $a.$

Eine Potenz besteht immer aus einer Basis (Grundzahl) und einem Exponenten (Hochzahl).

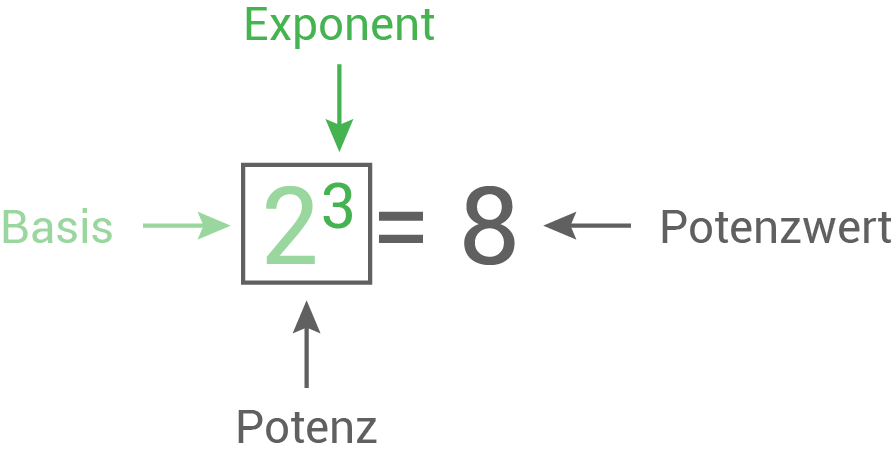potenzen

Man sagt: „Zwei hoch drei“

Beispiele

$8^3=8\cdot 8\cdot 8=512$
$4^5=4\cdot 4\cdot 4\cdot 4\cdot 4=1024$

$(-5)^2=(-5)\cdot (-5)=25$
$-5^2=-(5\cdot 5)=-25$

$0,5^3=0,5\cdot 0,5\cdot 0,5=0,125$
$\left(\dfrac{1}{2}\right)^3=\dfrac{1}{2}\cdot \dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{1}{8}$

$\sqrt{3}^4=\sqrt{3}\cdot \sqrt{3}\cdot \sqrt{3}\cdot \sqrt{3}=3\cdot 3=9$
$\sqrt{3}^3=\sqrt{3}\cdot \sqrt{3}\cdot \sqrt{3}=3 \sqrt{3}$

Es gibt auch Potenzen, die als Exponent Null oder eine negative Zahl haben.

Definitionen

$a^0=1$

$a^{-n}=\dfrac{1}{a^n} \quad (a\neq 0,n\in \mathbb{N})$

Beispiele

$6^0=1$

$1\,000^0=1$

$2^{-3}=\dfrac{1}{2^3}=\dfrac{1}{8}$
$4^{-2}=\dfrac{1}{4^2}=\dfrac{1}{16}$

$(-5)^{-2}=\dfrac{1}{(-5)^2}=\dfrac{1}{25}$
$(-5)^{-3}=\dfrac{1}{(-5)^3}=-\dfrac{1}{125}$

$\sqrt{7}^{-2}=\dfrac{1}{\sqrt{7}^2}=\dfrac{1}{7}$
$\sqrt{1}^{-3}=\dfrac{1}{\sqrt{1}^3}=\dfrac{1}{1}=1$