Lerninhalte in Mathe

Digitales Schulbuch

Inhaltsverzeichnis

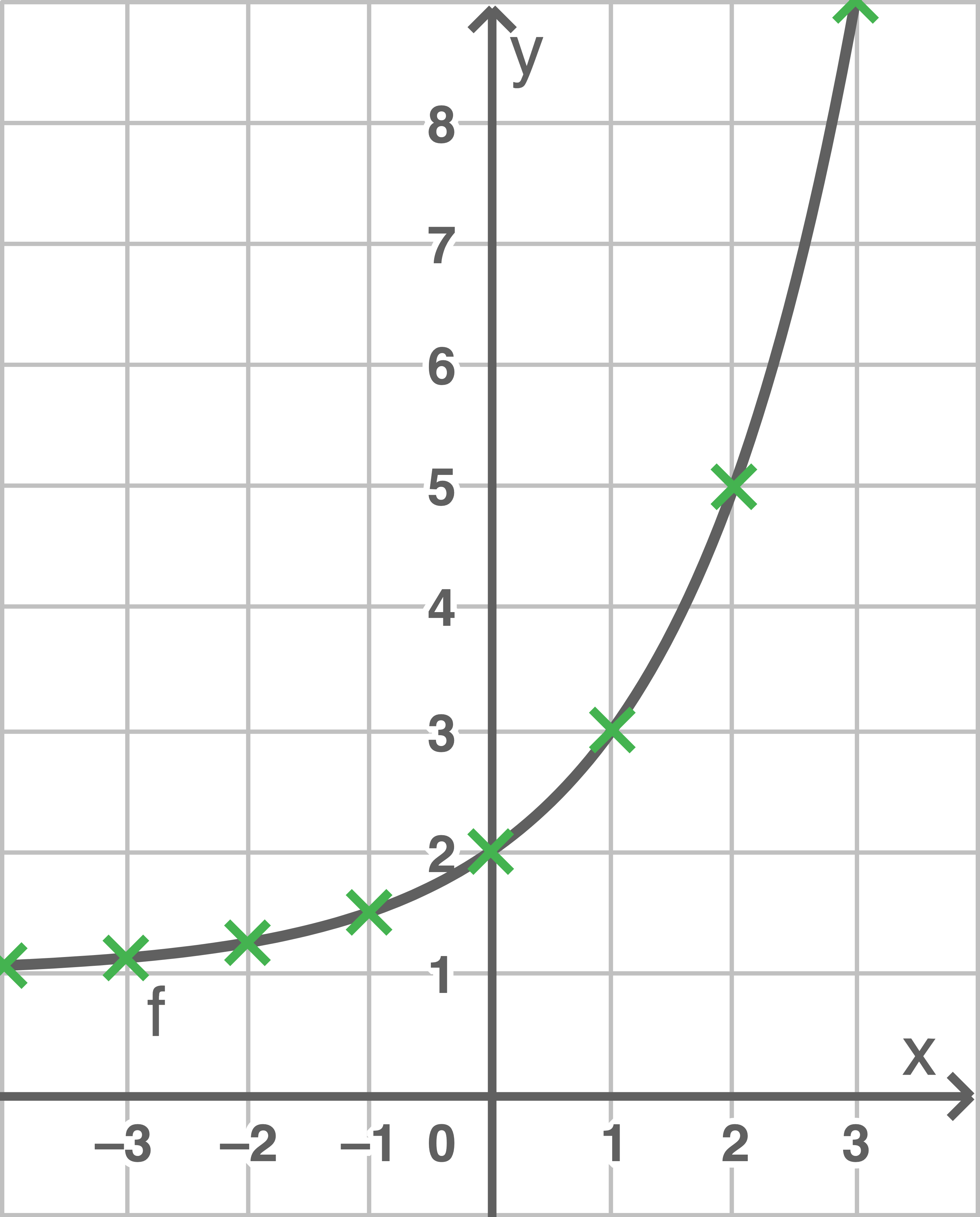
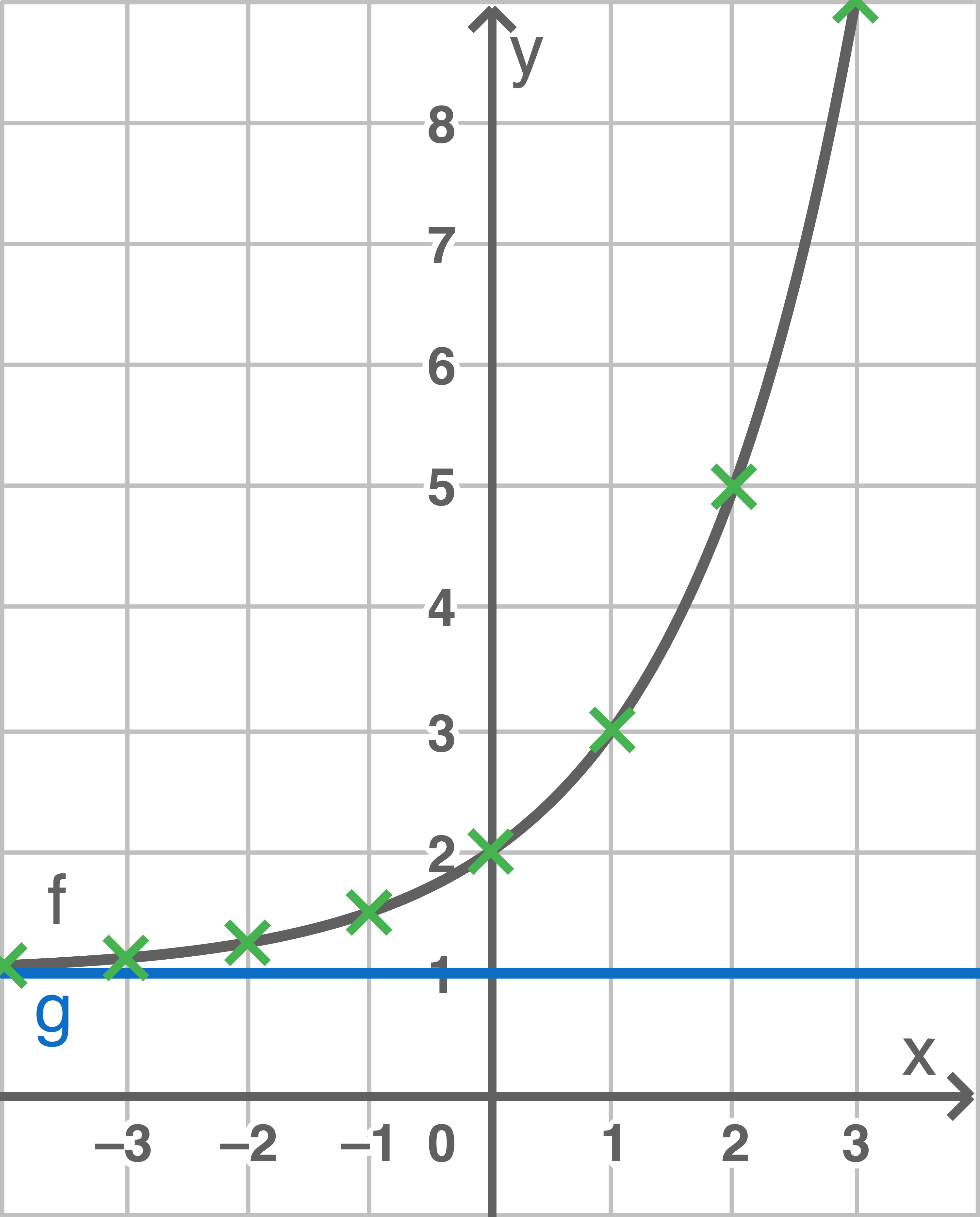
Exponentialfunktion

Definition

Eine Funktion $f$ mit $f(x)=c\cdot a^x$ wird als Exponentialfunktion zur Basis $a$ mit $a\gt 0$ bezeichnet.

Eigenschaften

Am Beispiel der Exponentialfunktion $f$ mit $f(x)=a^x,\, a\gt 0$

Der Graph verläuft immer oberhalb der $x$ -Achse, da $a^x$ für alle $x$ -Werte positiv ist.
Der Graph verläuft immer durch den Punkt $(0\mid 1)$ , da $a^0=1.$

Für $a\gt 1$ gilt: Die Funktionswerte $f(x)$ wachsen mit zunehmendem $x.$
Für $a\gt 1$ gilt: Der Graph nähert sich in negativer $x$ -Richtung der $x$ -Achse.

Für $0\lt a\lt 1$ gilt: Der Graph nähert sich in positiver $x$ -Richtung der $x$ -Achse.
Für $0\lt a\lt 1$ gilt: Die Funktionswerte $f(x)$ fallen mit zunehmendem $x.$

Beispiele

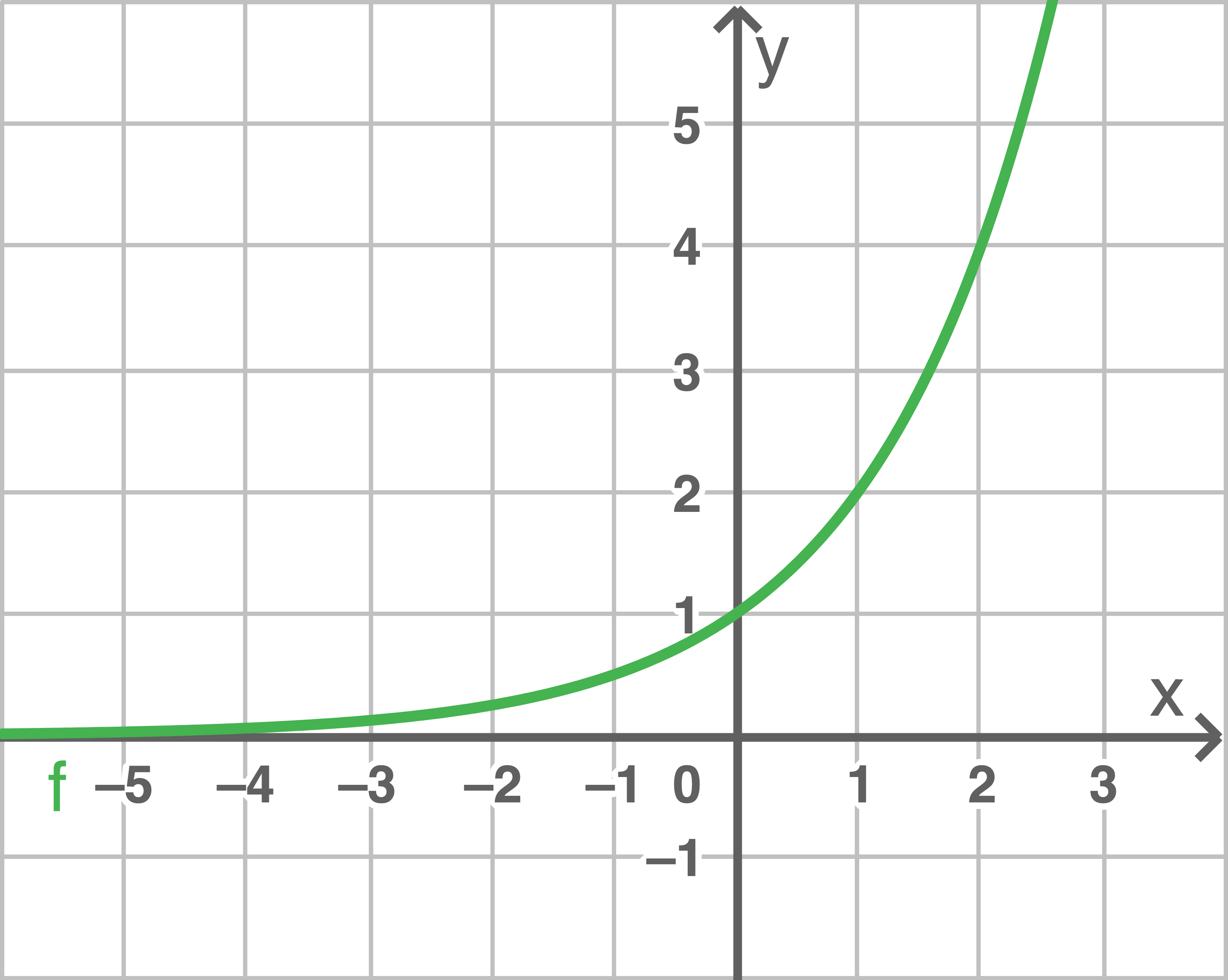
digitales schulbuch mathe gymnasium klasse 9

Beispiel für $\scriptsize a\gt 1$ mit $\scriptsize f(x)=2^x$

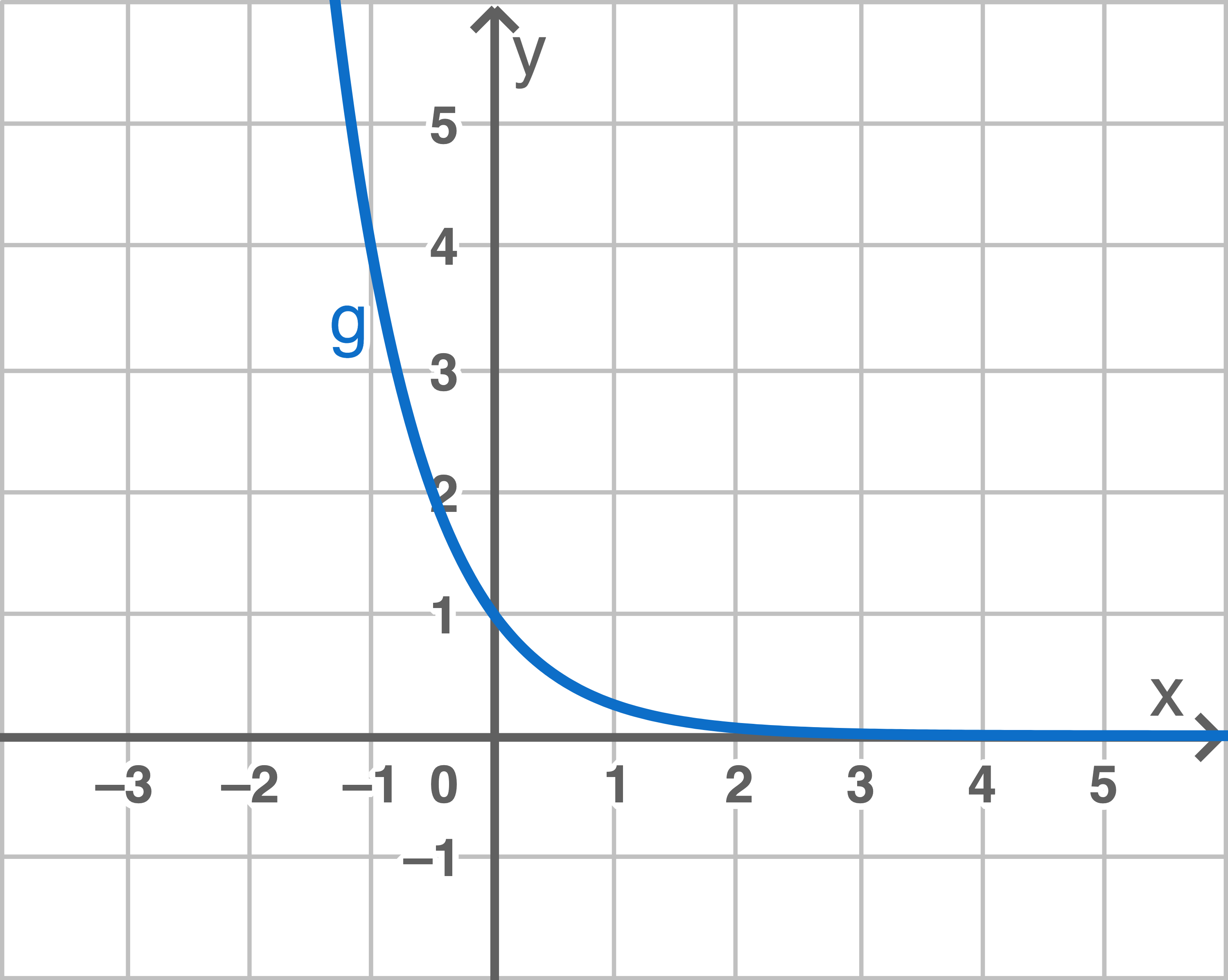
digitales schulbuch mathe gymnasium klasse 9

Beispiel für $\scriptsize 0\lt a\lt 1$ mit $\scriptsize g(x)=0,25^x$

1

a)

Wertetabelle anzeigen

b)

digitales schulbuch mathe gymnasium klasse 9

c)

Gerade: $y=1$ bzw. in neuer Schreibweise: $g(x)=1$

digitales schulbuch mathe gymnasium klasse 9

2

a)

$g(2)=3^2+3=9+3=12$

An der Stelle $x=2$ nimmt $g$ den Funktionswert $12$ und nicht $9$ an.

Der Punkt $A$ liegt also nicht auf dem Graphen von $g.$

b)

$g(5)=2^5+1=32+1=33$

Der Punkt $A$ liegt also auf dem Graphen von $g.$

c)

$g(3)=0,5\cdot 4^3=0,5\cdot 64=32$

An der Stelle $x=3$ nimmt $g$ den Funktionswert $32$ und nicht $33$ an.

Der Punkt $A$ liegt also nicht auf dem Graphen von $g.$

d)

$g(0)=1,5\cdot 7^0+2\cdot 0+1=1,5\cdot 1+1=2,5$

Der Punkt $A$ liegt also auf dem Graphen von $g.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?