Exponentialgleichungen und Logarithmus

Bisher wurden Exponentialfunktionen näher angeschaut.

Beispiel
$f(x)=3^x$

Es gibt aber auch sogenannte Exponentialgleichungen.

Beispiel
$3^x=27$

Mit den bisher behandelten Methoden ist es noch nicht möglich, Exponentialgleichungen zu lösen. Deswegen wird ein neues Lösungsverfahren benötigt: Der Logarithmus.

Definition

Der Logarithmus $\boldsymbol{\log_a(b)}$ zur Basis $\boldsymbol{a}$ ist die Hochzahl, mit der $a$ potenziert wird, um $b$ zu erhalten $(a,\,b\gt 0).$

Für $x=\log_a(b)$ gilt $a^x=b.$

Beachte: Für die Basis $10$ wird statt $\log_{10}(b)$ die Abkürzung $\log(b)$ verwendet.

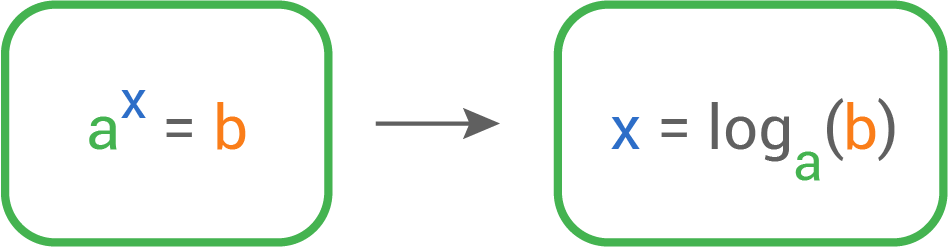Man sagt: x ist der Logarithmus von b zur Basis a.

Beispiel

$\begin{array}[t]{rll} 3^x&=&27&\quad \scriptsize \mid\;\log \\[5pt] x&=&\log_3(27)& \\[5pt] x&=&3 \end{array}$

Frage zum Lösen: Mit welcher Zahl muss $3$ potenziert werden, um $27$ zu erhalten? Die Antwort ist 3, denn: $3^3=27.$

Weiteres Beispiel

$\begin{array}[t]{rll} 10^x&=&10\,000&\quad \scriptsize \mid\;\log \\[5pt] x&=&\log(10\,000)& \\[5pt] x&=& 4 \end{array}$

Frage zum Lösen: Mit welcher Zahl muss $10$ potenziert werden, um $10\,000$ zu erhalten? Die Antwort ist 4, denn: $10^4=10\,000.$