Wahrscheinlichkeitsverteilung

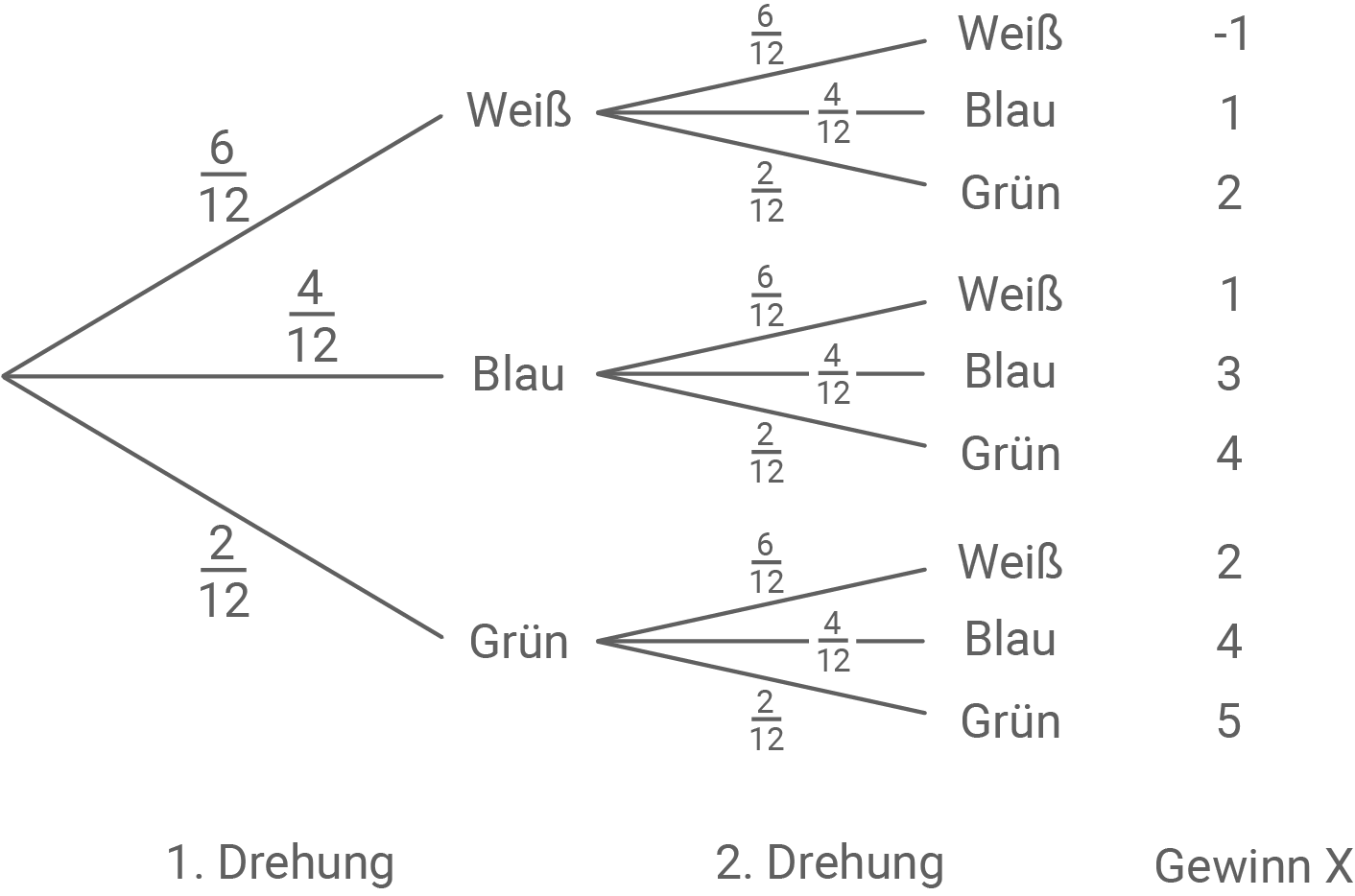
Das nebenstehende Glücksrad wird zweimal gedreht.

gluecksrad zufallsgroesse gymnasium klasse 9

Dabei gilt:

Weißes Feld: Kein Gewinn
Blaues Feld: $2\,€$ Gewinn
Grünes Feld: $3\,€$ Gewinn

Der Spieleinsatz liegt bei $1\,€.$

Mithilfe eines Baumdiagramms kann übersichtlich dargestellt werden, wie hoch die Wahrscheinlichkeit eines bestimmten Gewinns ist.

Der Gewinn ist dabei die Differenz aus Auszahlung und Spieleinsatz.

Anhand des Baumdiagramms lassen sich die verschiedenen Werte der Zufallsgröße $X$ ablesen:

$x_1=-1$
$x_2=1$
$x_3=2$
$x_4=3$
$x_5=4$
$x_6=5$

Dabei bilden alle Ergebnisse, die zu dem Gewinn $1\,€$ führen, ein Ereignis.

Für dieses Ereignis wird $\boldsymbol{X=1}$ geschrieben.
Die Ergebnisse (Weiß; Blau) und (Blau; Weiß) führen zum Ereignis $\boldsymbol{X=1.}$
$\boldsymbol{P(X=1)}$ gibt an, mit welcher Wahrscheinlichkeit Spielende einen Gewinn von $1\,€$ machen.

Die Wahrscheinlichkeit wird hier wie folgt berechnet:

$\quad P(X=1)$

$\begin{array}[t]{rll} &=&P(\text{Weiß; Blau})+P(\text{Blau; Weiß}) &\\[5pt] &=&\dfrac{6}{12}\cdot \dfrac{4}{12}+\dfrac{4}{12}\cdot \dfrac{6}{12} &\\[5pt] &=&\dfrac{1}{3}\\[5pt] \end{array}$

Wahrscheinlichkeitsverteilung einer Zufallsgröße $X$

In einer Tabelle lässt sich die Wahrscheinlichkeitsverteilung der Zufallsgröße $X$ darstellen:

Tabelle anzeigen

Gewinn $\color{#ffffff}{x_i}$	$-1$	$1$	$2$	$3$	$4$	$5$
Wahrscheinlichkeit $\color{#ffffff}{P(X=x_i)}$	$\dfrac{6}{12}\cdot \dfrac{6}{12}$ $=\dfrac{1}{4}$	$\dfrac{1}{3}$	$\dfrac{6}{12}\cdot \dfrac{2}{12}+\dfrac{2}{12}\cdot \dfrac{6}{12}$ $=\dfrac{1}{6}$	$\dfrac{4}{12}\cdot \dfrac{4}{12}$ $=\dfrac{1}{9}$	$\dfrac{4}{12}\cdot \dfrac{2}{12}+\dfrac{2}{12}\cdot \dfrac{4}{12}$ $=\dfrac{1}{9}$	$\dfrac{2}{12}\cdot \dfrac{2}{12}$ $=\dfrac{1}{36}$

Definition

Die Wahrscheinlichkeitsverteilung einer Zufallsgröße $X$ lässt sich in einer Tabelle darstellen. Darin werden alle Werte $x_1,x_2,...,x_n$ notiert, die $X$ annimmt, sowie die zugehörigen Wahrscheinlichkeiten $P(X=x_i).$

Bei einem Stadtfest steht ein Glücksrad mit drei gleichgroßen Segmenten.

Segment 1: Spieler*in erhält eine Jahreskarte fürs Hallenbad.
Segment 2: Spieler*in erhält eine Tüte Gummibärchen.
Segment 3: Spieler*in erhält keinen Preis.

Das Glücksrad darf zweimal hintereinander gedreht werden.

Die Zufallsgröße $X$ gibt die Anzahl der Gewinne an.

Welche Werte kann $X$ bei diesem Glücksspiel annehmen?

Bestimme alle Ergebnisse, die zum Ereignis $X=1$ führen.

Bestimme alle Ergebnisse, die zum Ereignis $X=2$ führen.

Wie hoch ist die Wahrscheinlichkeit, zwei Gewinne zu erzielen?

Wie hoch ist die Wahrscheinlichkeit, keine Gewinne zu erzielen?

Mit dem nebenstehenden Gefäß wird ein Glücksspiel durchgeführt.

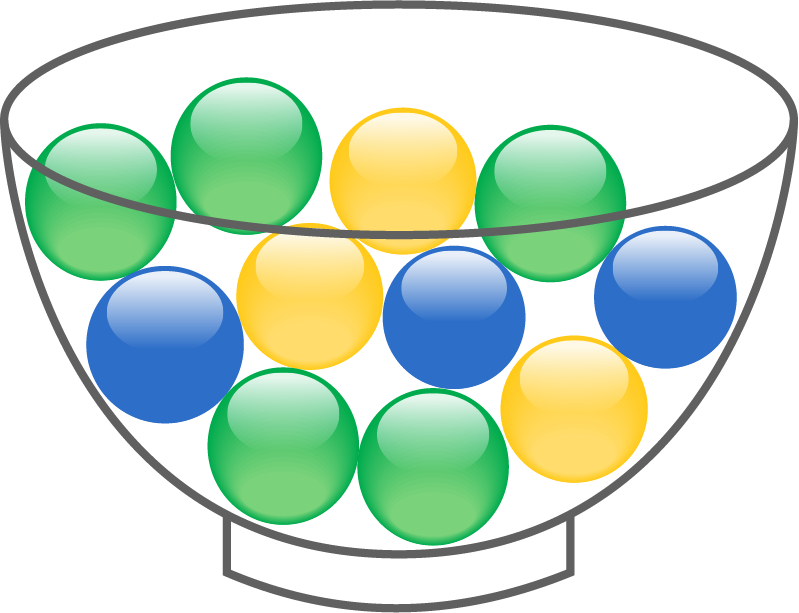Gefäß mit Kugeln - Zufallsgröße Gymnasium Klasse 9

Der Spieleinsatz beträgt $2,50\,€.$ Die Spieler*innen dürfen zwei Kugeln ohne Zurücklegen ziehen.

Folgende Farbkombinationen der Kugeln führen zu einem Gewinn:

Gelb + Gelb: $4,50\,€$ Gewinn
Gelb + Grün: $2,00\,€$ Gewinn
Blau + Blau: $4,50\,€$ Gewinn
Blau + Gelb: $3,00\,€$ Gewinn

Die Reihenfolge in der die Kugeln gezogen werden, spielt keine Rolle.

Stelle eine Tabelle mit der Wahrscheinlichkeitsverteilung für den Gewinn aus Sicht der Spieler*innen auf.

Ben zieht zwei Kugeln.

Wie hoch ist die Wahrscheinlichkeit, dass Ben mit Gewinn aus dem Spiel geht?

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

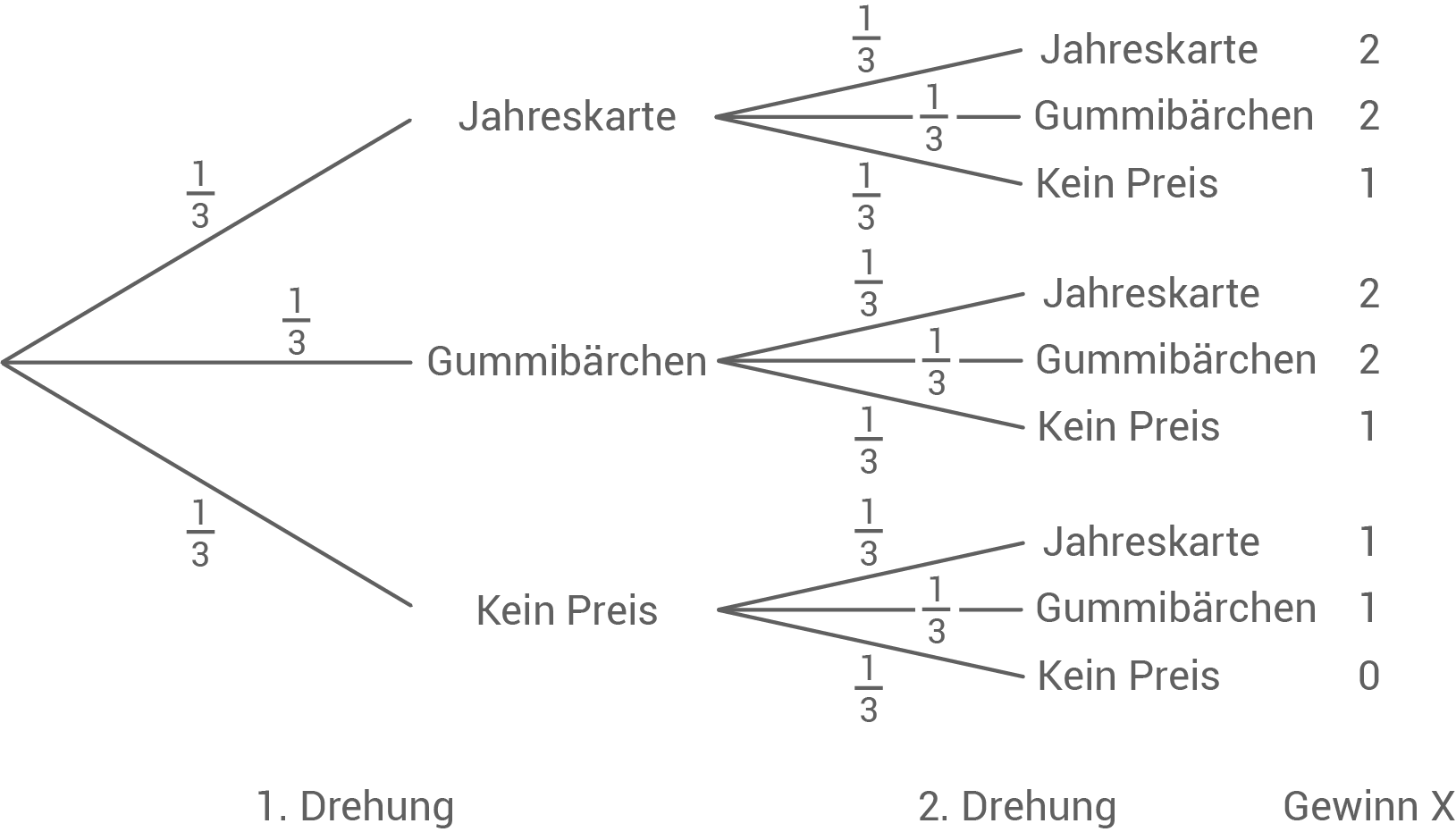
zufallsgroesse mathe zufall baumdiagramm

Anhand des Baumdiagramms erkennt man, dass $X$ folgende Werte annehmen kann:

$X=0$
$X=1$
$X=2$

Folgende Ergebnisse führen zum Ereignis $X=1$ :

(Jahreskarte; Kein Preis)
(Gummibärchen; Kein Preis)
(Kein Preis; Jahreskarte)
(Kein Preis; Gummibärchen)

Folgende Ergebnisse führen zum Ereignis $X=2$ :

(Jahreskarte; Jahreskarte)
(Jahreskarte; Gummibärchen)
(Gummibärchen; Jahreskarte)
(Gummibärchen; Gummibärchen)

$\begin{array}[t]{rll} P(X=2) &=& \dfrac{1}{3}\cdot \dfrac{1}{3}+\dfrac{1}{3}\cdot \dfrac{1}{3}+\dfrac{1}{3}\cdot \dfrac{1}{3}+\dfrac{1}{3}\cdot \dfrac{1}{3} \\[5pt] &=& \dfrac{4}{9} \end{array}$

$\begin{array}[t]{rll} P(X=0) &=& \dfrac{1}{3}\cdot \dfrac{1}{3}\\[5pt] &=& \dfrac{1}{9} \end{array}$

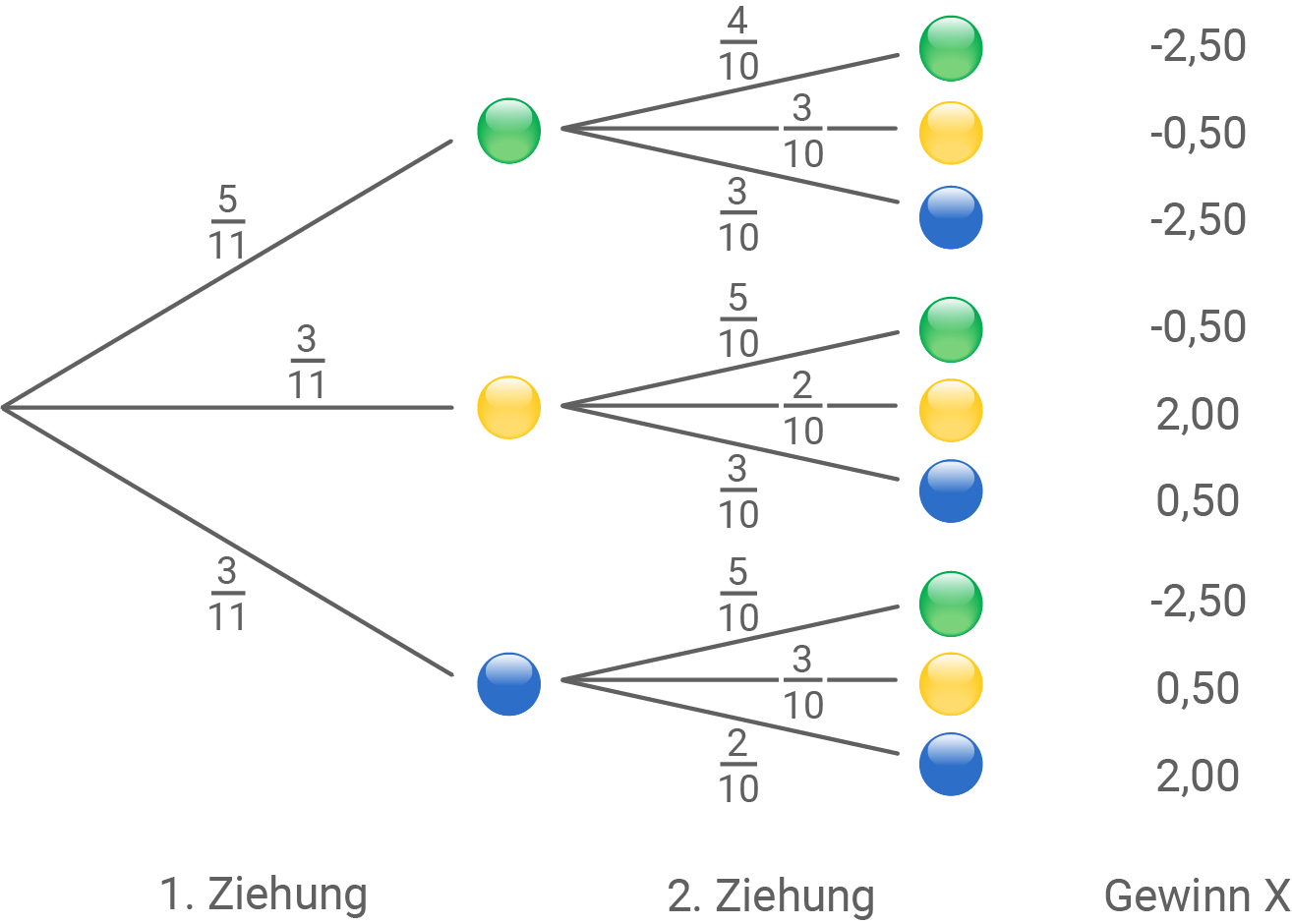
Baumdiagramm Kugeln ziehen - Gymnasium Klasse 9

Mithilfe des Baumdiagramms lässt sich schnell die Wahrscheinlichkeitsverteilung aufstellen:

Tabelle anzeigen

Gewinn $\color{#ffffff}{x_i}$	$-2,50$	$-0,50$	$0,50$	$2,00$
Wahrscheinlichkeit $\color{#ffffff}{P(X=x_i)}$	$\dfrac{5}{11}\cdot \dfrac{4}{10}+\dfrac{5}{11}\cdot \dfrac{3}{10}+\dfrac{3}{11}\cdot \dfrac{5}{10}$ $=\dfrac{5}{11}$	$\dfrac{5}{11}\cdot \dfrac{3}{10}+\dfrac{3}{11}\cdot \dfrac{5}{10}$ $=\dfrac{3}{11}$	$\dfrac{3}{11}\cdot \dfrac{3}{10}+\dfrac{3}{11}\cdot \dfrac{3}{10}$ $=\dfrac{9}{55}$	$\dfrac{3}{11}\cdot \dfrac{2}{10}+\dfrac{3}{11}\cdot \dfrac{2}{10}$ $=\dfrac{6}{55}$

$\begin{array}[t]{rll} P(\text{Gewinn})&=& P(X=0,50)+P(X=2,00) \\[5pt] &=& \dfrac{9}{55}+\dfrac{6}{55} \\[5pt] &=& \dfrac{15}{55} \\[5pt] &=& \dfrac{3}{11} \end{array}$

Ben geht mit einer Wahrscheinlichkeit von $\dfrac{3}{11}\approx 27\,\%$ mit Gewinn aus dem Spiel.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?