Sinus, Kosinus, Tangens
Bei diesem Thema geht es um Zusammenhänge zwischen den Seitenlängen und Winkelweiten in rechtwinkligen Dreiecken.
Sinus von
Kosinus von
Tangens von
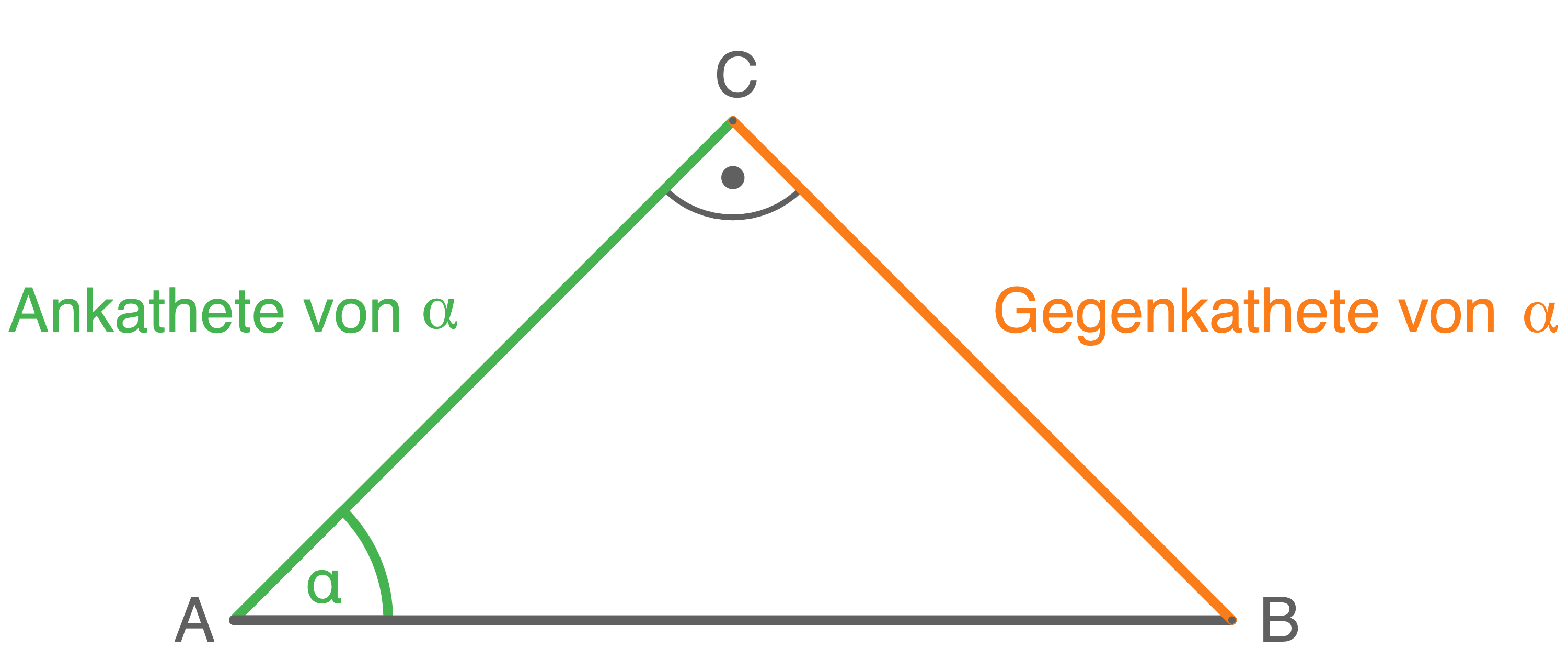
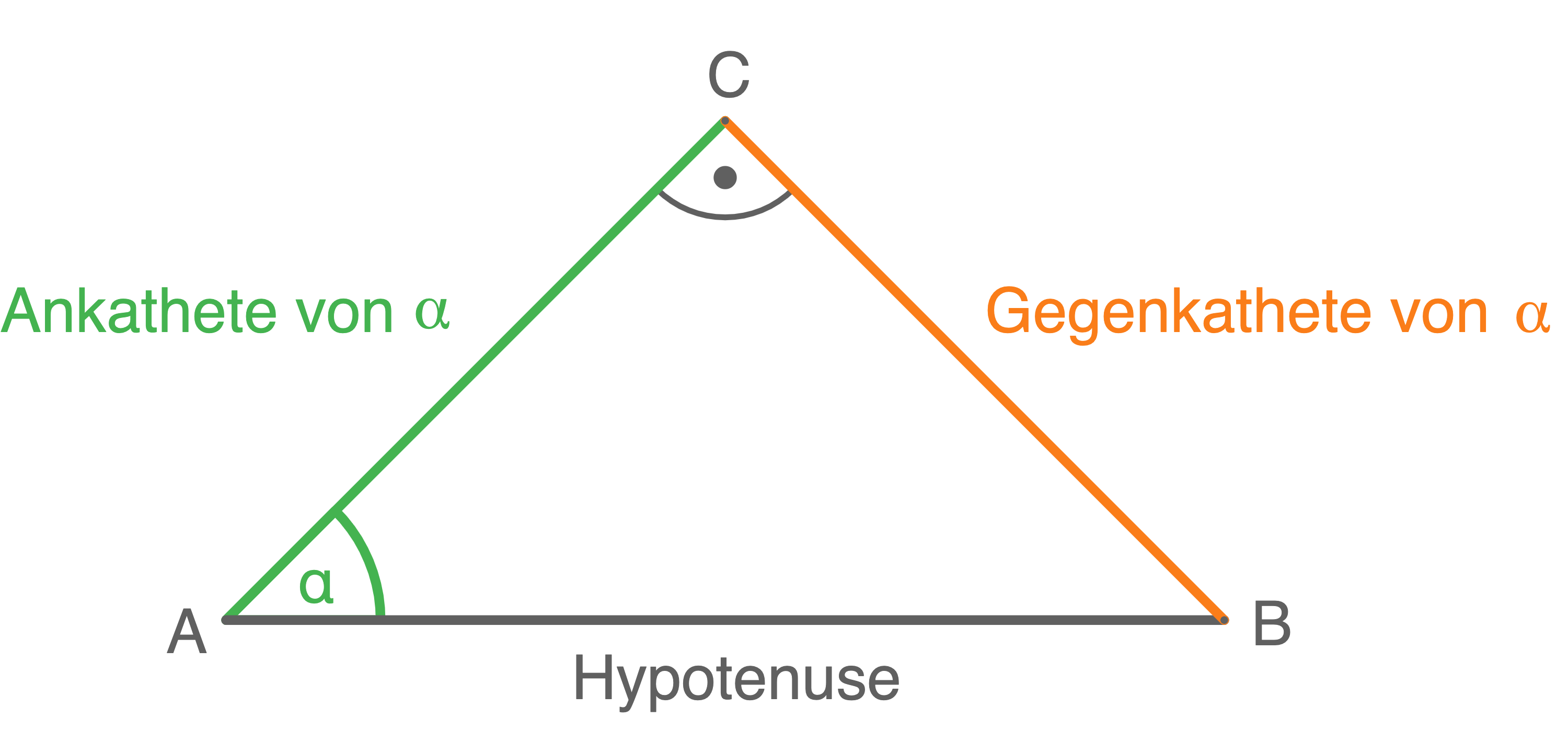
Hierfür werden zwei neue Begriffe benötigt:
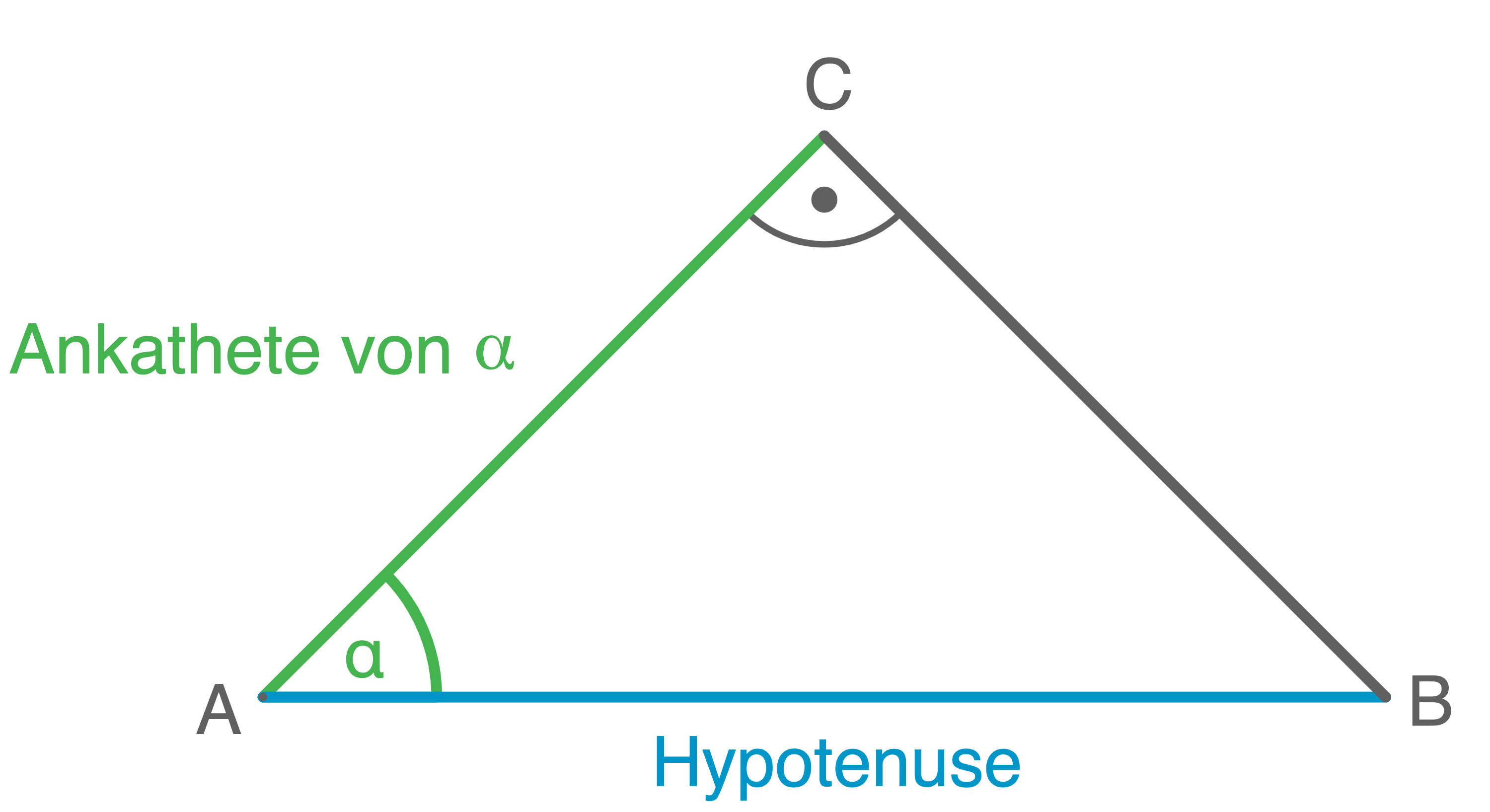
- Die Ankathete von
ist die Seite im Dreieck, die am Winkel
anliegt.
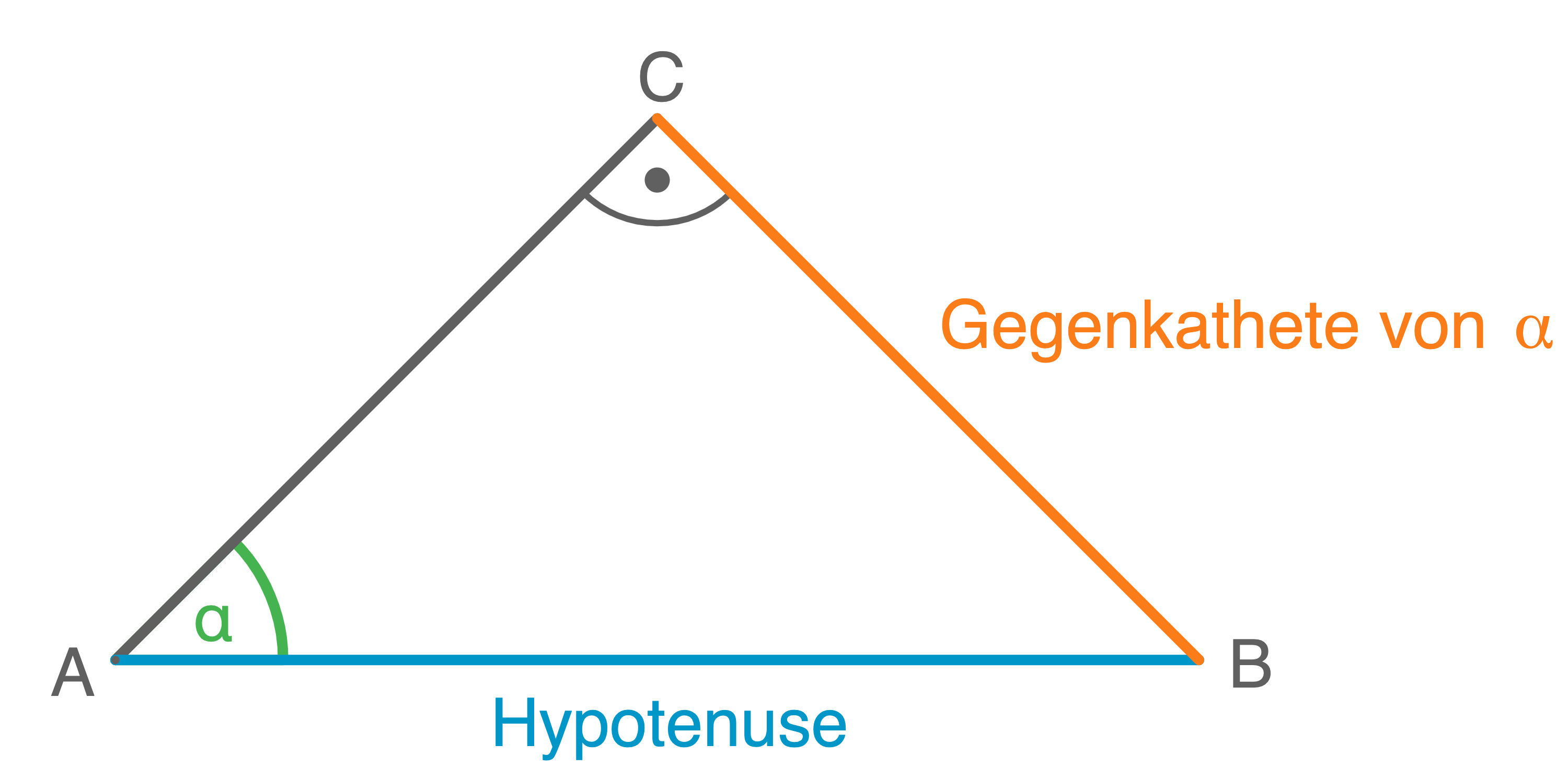
- Die Gegenkathete von
Sinus von
Definition
In einem rechtwinkligen Dreieck wird zu einem Winkel des Dreiecks das Streckenverhältnis 
als Sinus von bezeichnet.
als Sinus von
Wichtige Werte
Kosinus von
Definition
In einem rechtwinkligen Dreieck wird zu einem Winkel des Dreiecks das Streckenverhältnis 
als Kosinus von bezeichnet.
als Kosinus von
Wichtige Werte
Tangens von
Definition
In einem rechtwinkligen Dreieck wird zu einem Winkel des Dreiecks das Streckenverhältnis 
als Tangens von bezeichnet.
als Tangens von
Wichtige Werte
1
Gegeben ist das nebenstehende Dreieck.
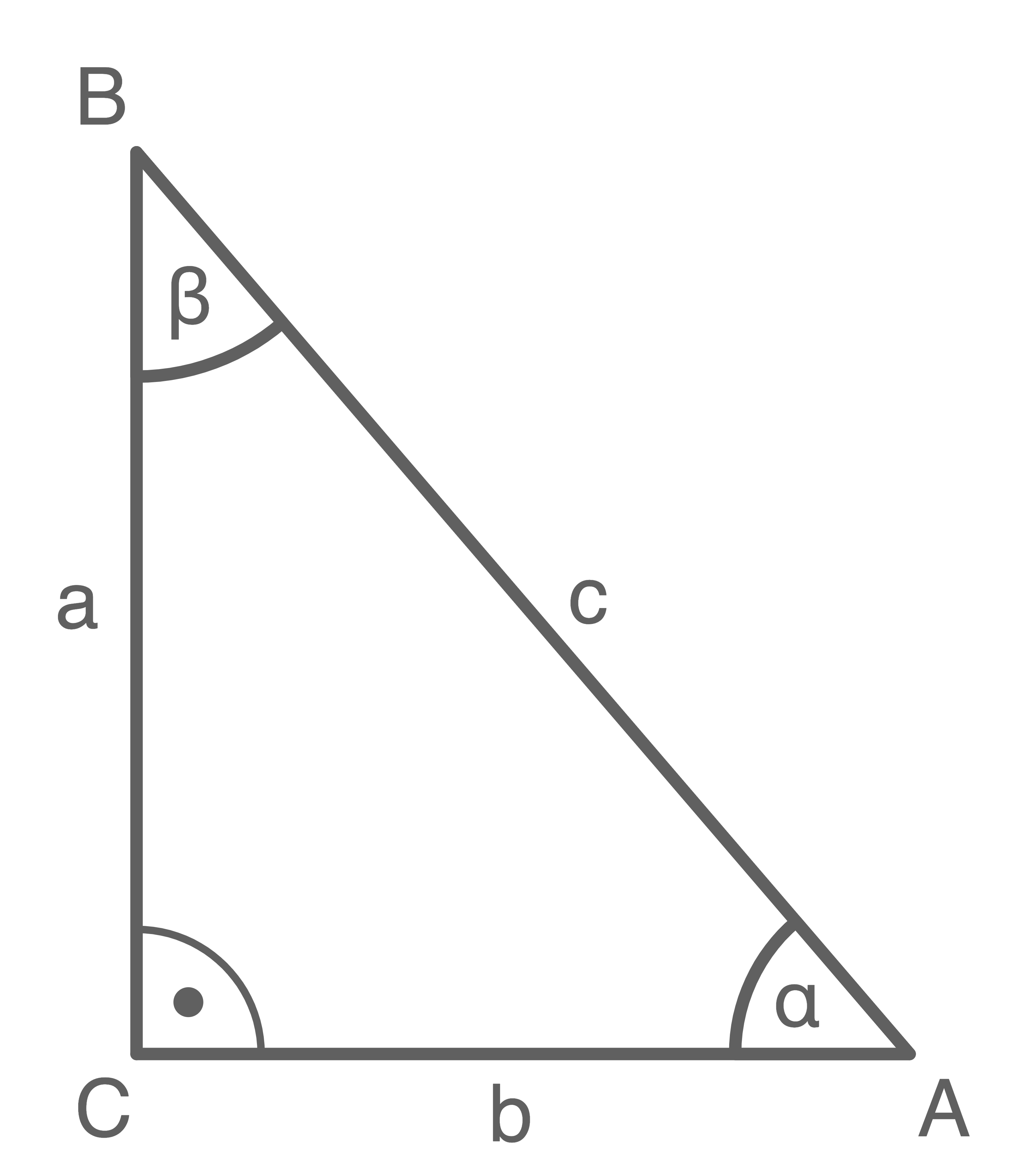
a)
Stelle eine Gleichung auf, die für dieses Dreieck den Sinus von wiedergibt.
b)
Stelle eine Gleichung auf, die für dieses Dreieck den Kosinus von wiedergibt.
c)
Stelle eine Gleichung auf, die für dieses Dreieck den Tangens von wiedergibt.
Gegeben sind nun folgende Seitenlängen:
d)
Berechne die Größe des Winkels 
e)
Welche zwei Möglichkeiten gibt es, die Größe des Winkels 
zu berechnen?
Stelle beide Gleichungen auf und zeige den jeweiligen Rechenweg auf.
2
Berechne die Größe der markierten Winkel.
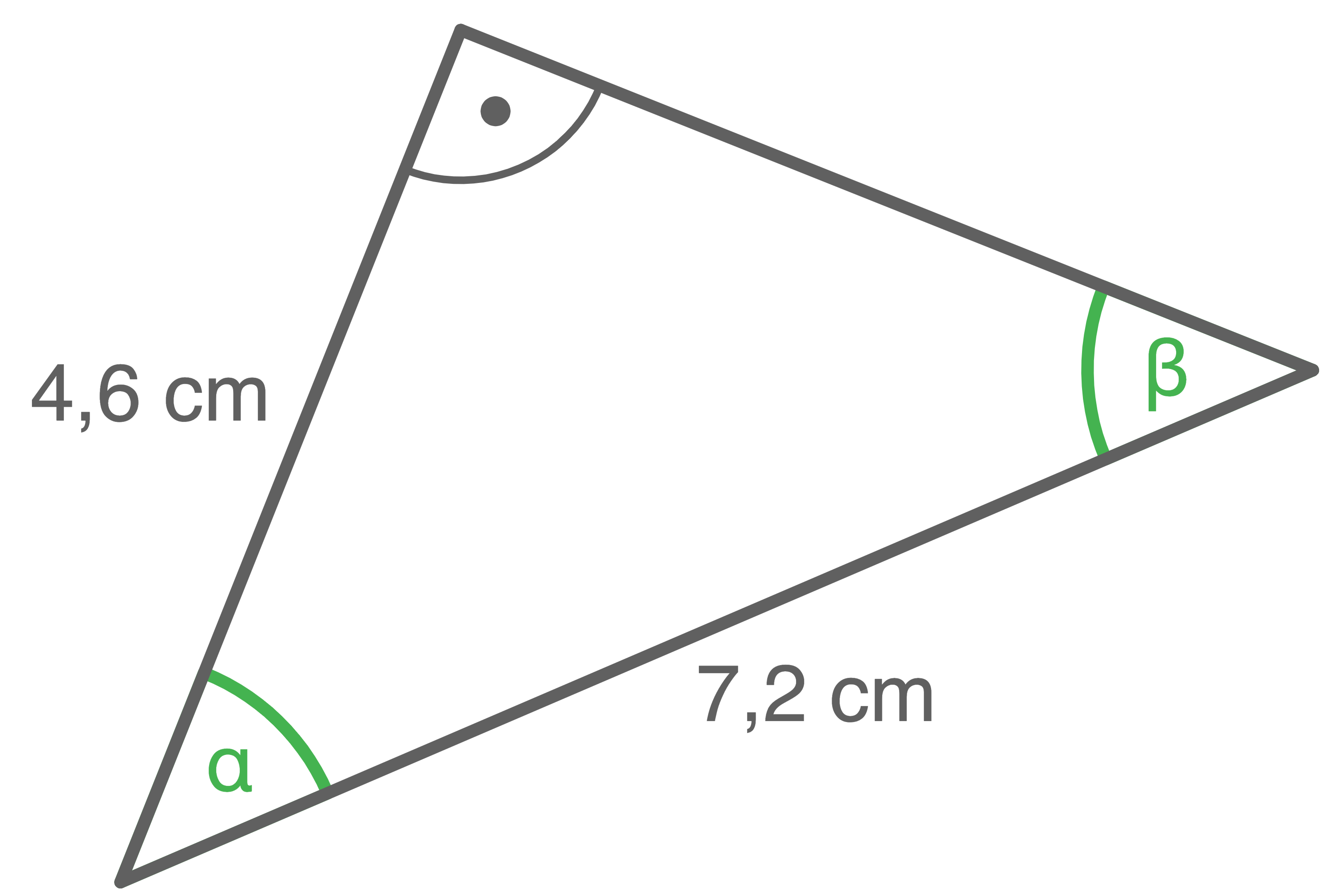
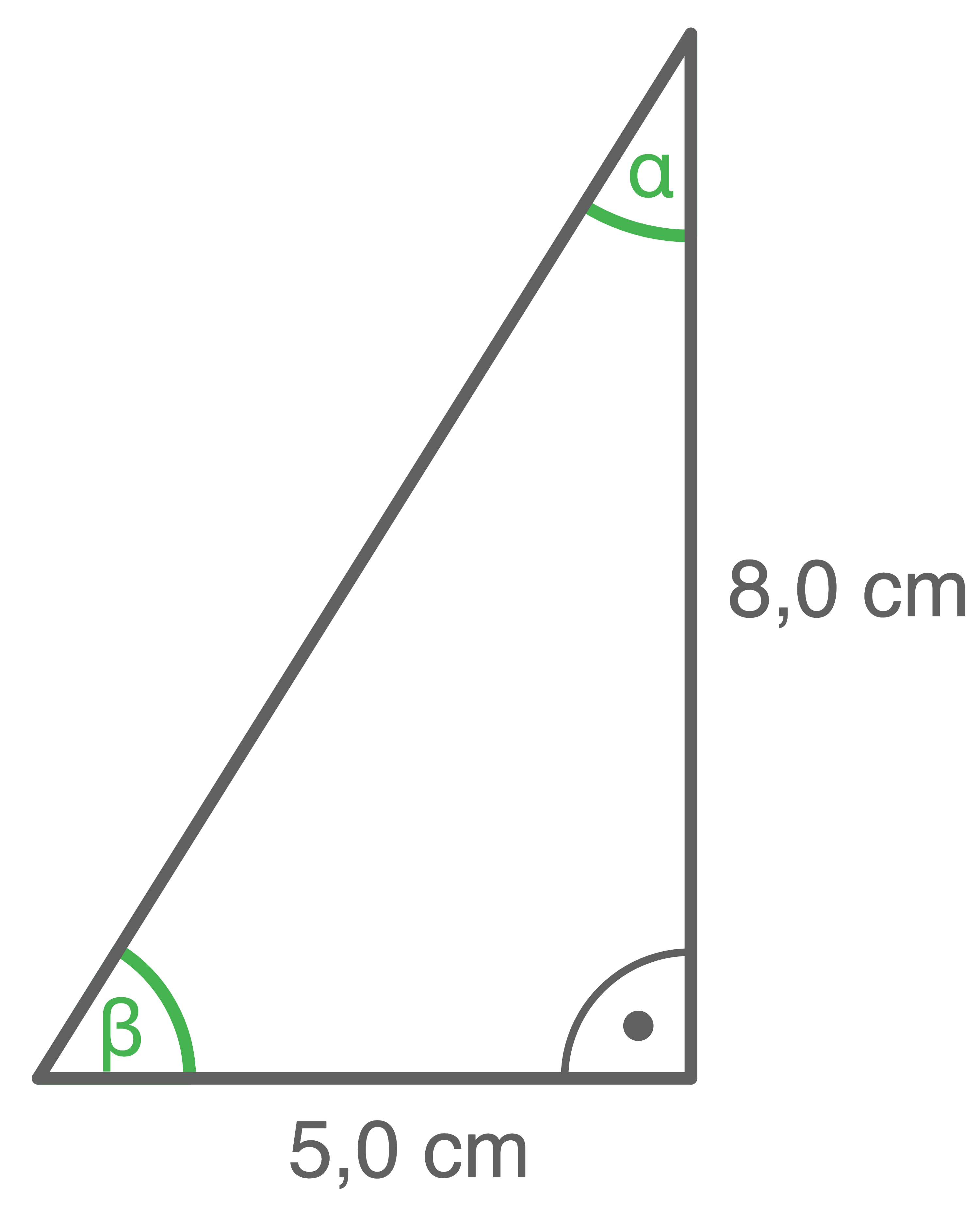
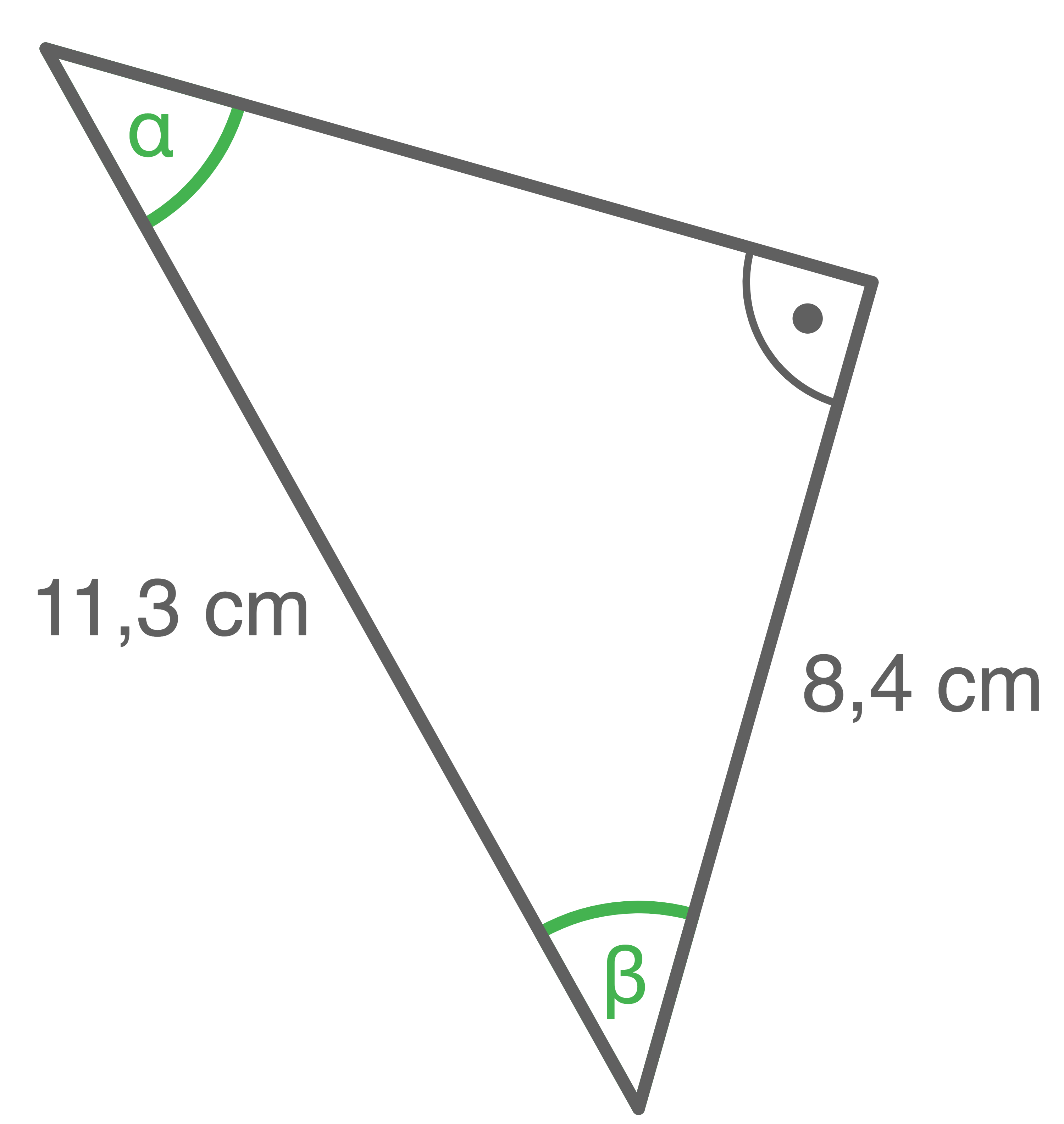
a)
b)
c)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Gegeben ist das nebenstehende Dreieck.
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{a}{b}& \\[5pt]
\tan(\alpha)&=& \dfrac{4,5\,\text{cm}}{5,2\,\text{cm}}&\\[5pt]
\tan(\alpha)&=& \dfrac{4,5}{5,2}&\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\alpha&\approx& 41^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/54d06e1fd82d230fe9117676865f3da3870f9c049c74ffe86a2a90a028e52150?color=5a5a5a)
a)
b)
c)
d)
e)
1. Möglichkeit: Berechnung über den Tangens von 
![\(\begin{array}[t]{rll}
\tan(\beta)&=& \dfrac{b}{a}& \\[5pt]
\tan(\beta)&=& \dfrac{5,2\,\text{cm}}{4,5\,\text{cm}}&\\[5pt]
\tan(\beta)&=& \dfrac{5,2}{4,5}&\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\tan(\beta)&\approx& 49^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/bfa2d0764c1ae3a4be29c38412d51a46028d6aa7ff01ada0772b2c3bd5ee5662?color=5a5a5a)
2. Möglichkeit: Berechnung über den Winkelsummensatz
![\(\begin{array}[t]{rll}
180^{\circ}&=&\alpha+\beta+\gamma &\quad \scriptsize \mid\;-\alpha \,\,\mid\;-\gamma \\[5pt]
\beta&=& 180^{\circ}-\alpha-\gamma \\[5pt]
\beta&=& 180^{\circ}-41^{\circ}-90^{\circ} \\[5pt]
\beta&=& 49^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4d7b46feb688998cd6bdf9305fae4f0d0968518bb2bd3a4e378f8b726f5de9e1?color=5a5a5a)
2
a)
1. Schritt: Größe des Winkels berechnen
![\(\begin{array}[t]{rll}
\cos(\alpha) &=&\dfrac{4,6\,\text{cm}}{7,2\,\text{cm}} \\[5pt]
\cos(\alpha) &=&\dfrac{4,6}{7,2} &\quad \scriptsize \mid\; \cos^{-1} \\[5pt]
\alpha &\approx& 50^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/8dec587387540553d740c4e4e693d1541020e04d6b2897fa2685ac9304d9c729?color=5a5a5a)
2. Schritt: Größe des Winkels berechnen
![\(\begin{array}[t]{rll}
\beta&=& 180^{\circ}-\alpha-90^{\circ} \\[5pt]
\beta&\approx& 180^{\circ}-50^{\circ}-90^{\circ} \\[5pt]
\beta&\approx& 40^{\circ}
\end{array}\)](https://mathjax.schullv.de/0ba58f0700ada233a4ffd038e60a3090f798ba441c3dba56b65b492ea84e18b1?color=5a5a5a)
b)
1. Schritt: Größe des Winkels berechnen
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{5,0\,\text{cm}}{8,0\,\text{cm}} \\[5pt]
\tan(\alpha)&=&\dfrac{5,0}{8,0} &\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha&\approx&32^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/93978f5e0a8e04e7b7e21b3c7e7f4270a5d205d732ef114c0ff96472fe603b8c?color=5a5a5a)
2. Schritt: Größe des Winkels berechnen
![\(\begin{array}[t]{rll}
\beta&=&180^{\circ}-\alpha-90^{\circ} \\[5pt]
\beta&\approx&180^{\circ}-32^{\circ}-90^{\circ} \\[5pt]
\beta&\approx&58^{\circ}
\end{array}\)](https://mathjax.schullv.de/372b720d1a94b9ed4e18b6a1b3599a9c35807f0fa9d06f0295f9a440058d2667?color=5a5a5a)
c)
1. Schritt: Größe des Winkels berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{8,4\,\text{cm}}{11,3\,\text{cm}} \\[5pt]
\sin(\alpha)&=&\dfrac{8,4}{11,3} &\quad \scriptsize \mid\; \sin^{-1} \\[5pt]
\alpha&\approx&48^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/163bd71a7f0980e9b60338c4b9d3735ec2d606bb768cfcc5f9ffe4f14e08e8df?color=5a5a5a)
2. Schritt: Größe des Winkels berechnen
![\(\begin{array}[t]{rll}
\beta&=&180^{\circ}-\alpha-90^{\circ} \\[5pt]
\beta&\approx&180^{\circ}-48^{\circ}-90^{\circ} \\[5pt]
\beta&\approx&42^{\circ}
\end{array}\)](https://mathjax.schullv.de/93ea36a88d70f4d0bf66efdf5f00f0142340c9db05a8c80f976056a9978b3560?color=5a5a5a)