Satz des Pythagoras mit Umkehrung
In einem rechtwinkligen Dreieck gibt es drei Seiten: zwei Katheten und eine Hypotenuse.
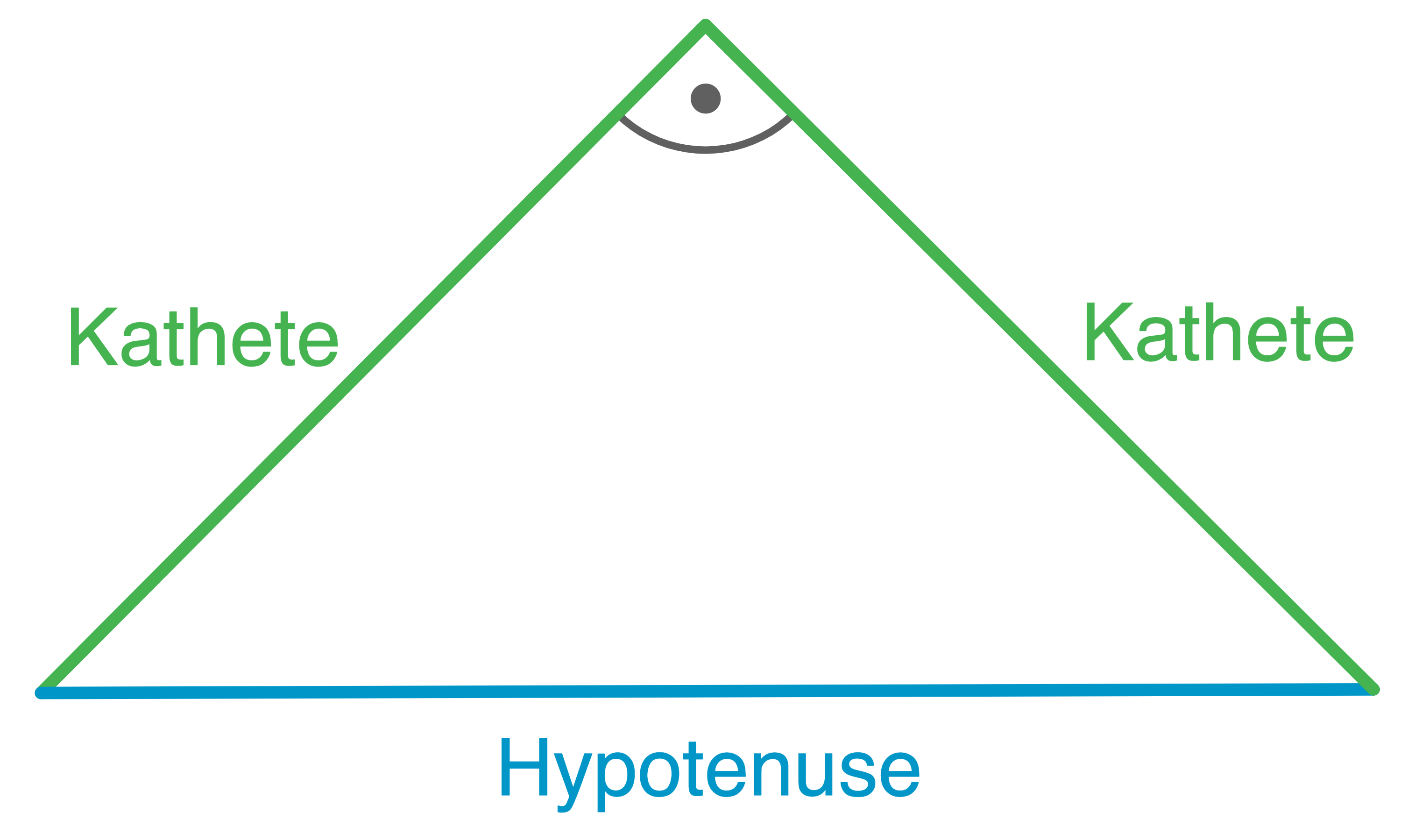Die Katheten schließen den rechten Winkel ein. Die Hypotenuse liegt gegenüber vom rechten Winkel. Die Hypotenuse ist immer die längste Seite in einem rechtwinkligen Dreieck.
Definition: Satz des Pythagoras
Gegeben ist ein Dreieck mit den Seitenlängen 
und 
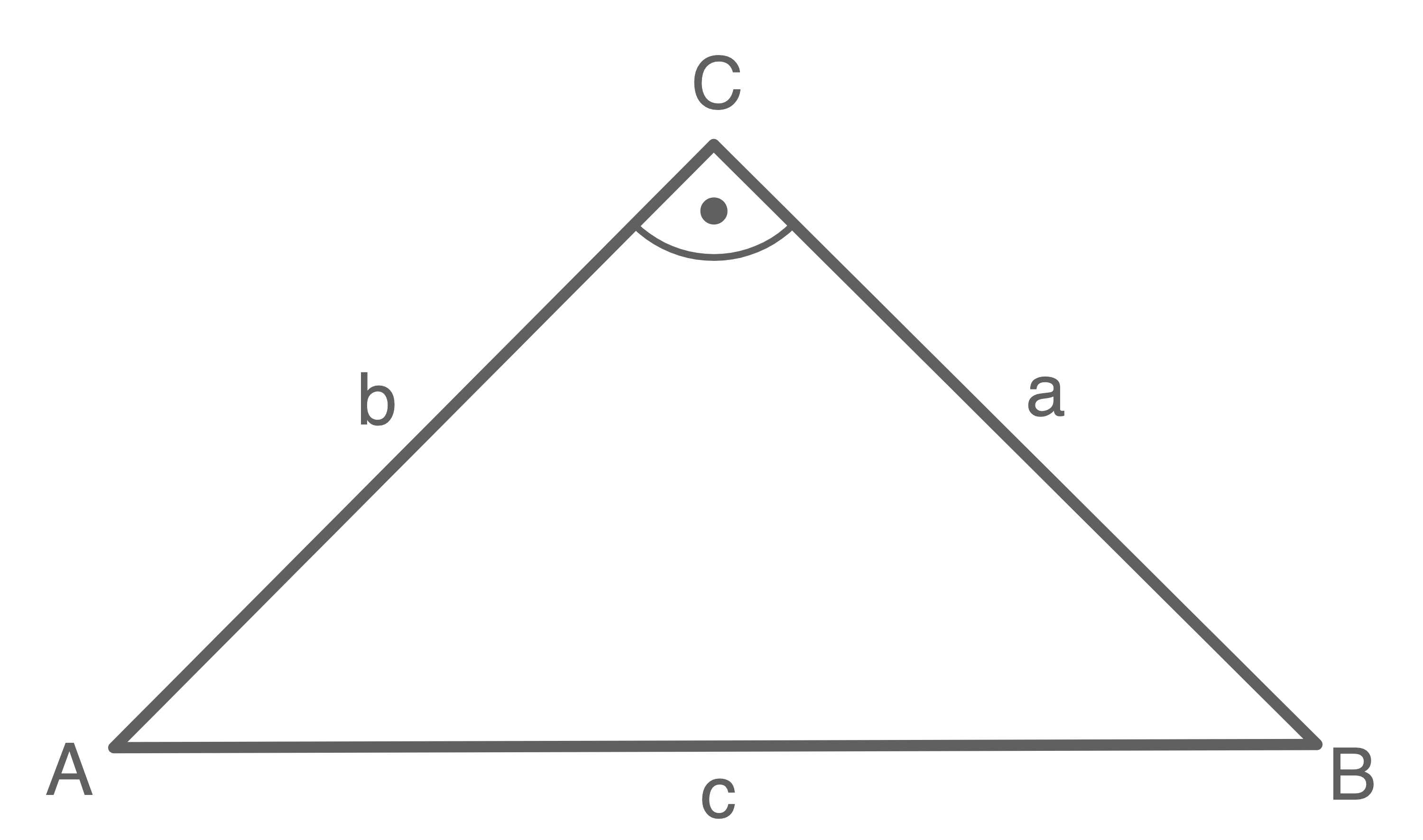Ist das Dreieck rechtwinklig mit der Hypotenuse 
gilt 
Definition: Umkehrung des Satz des Pythagoras
Gegeben ist ein Dreieck mit den Seitenlängen
1
Gib eine Gleichung an, die den Zusammenhang zwischen den Seitenlängen des rechtwinkligen Dreiecks nach dem Satz des Pythagoras wiedergibt.
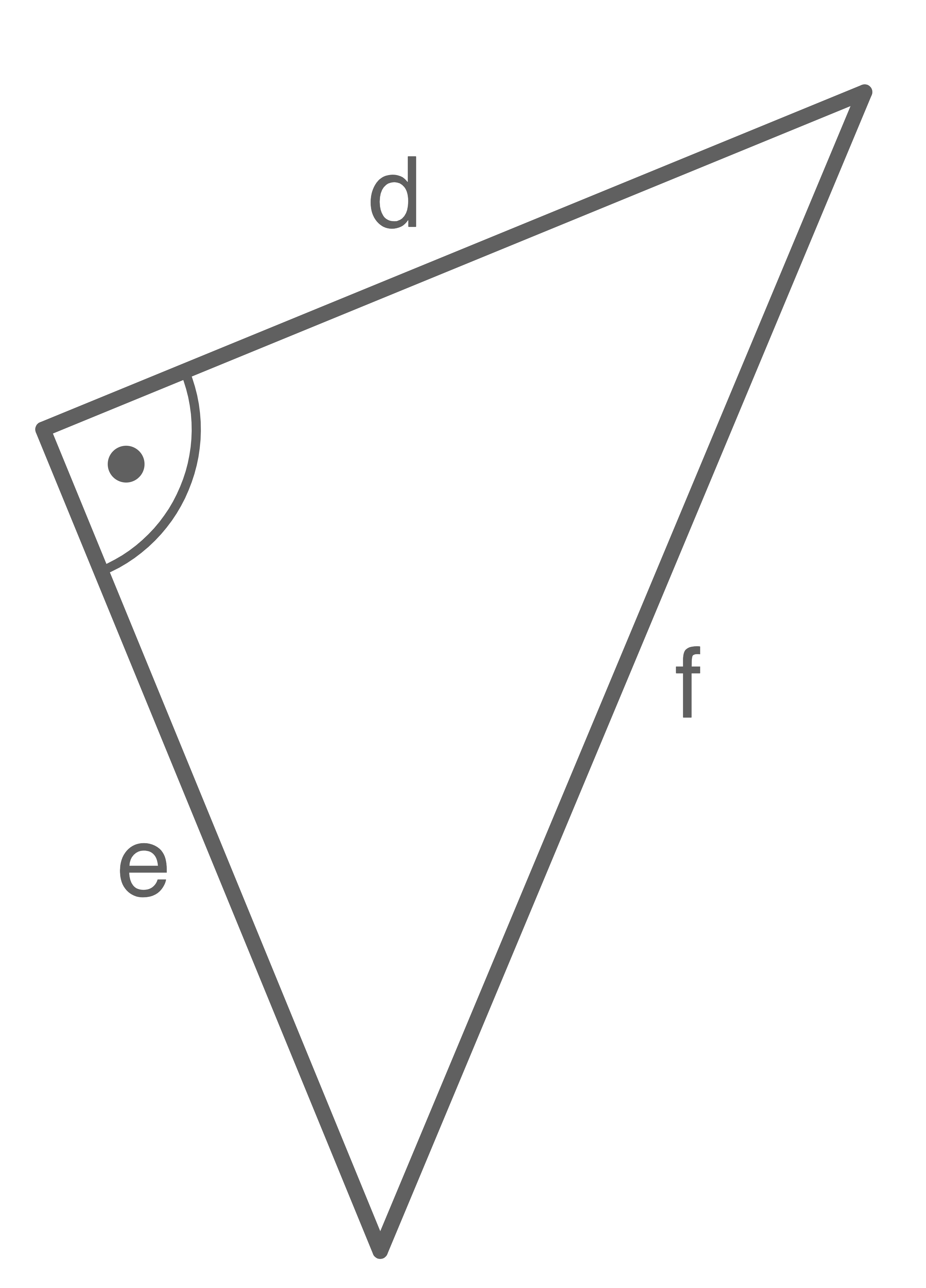
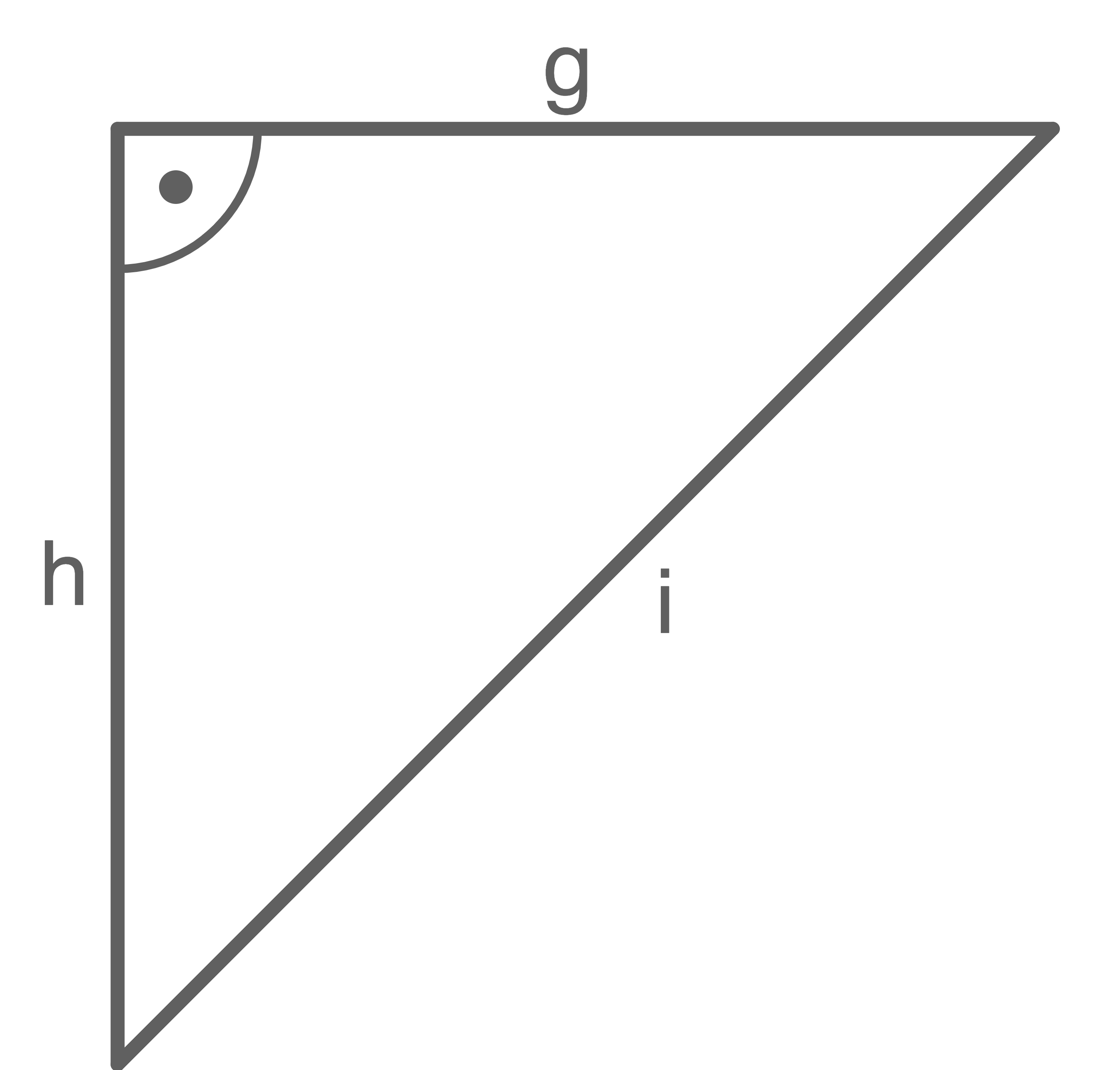
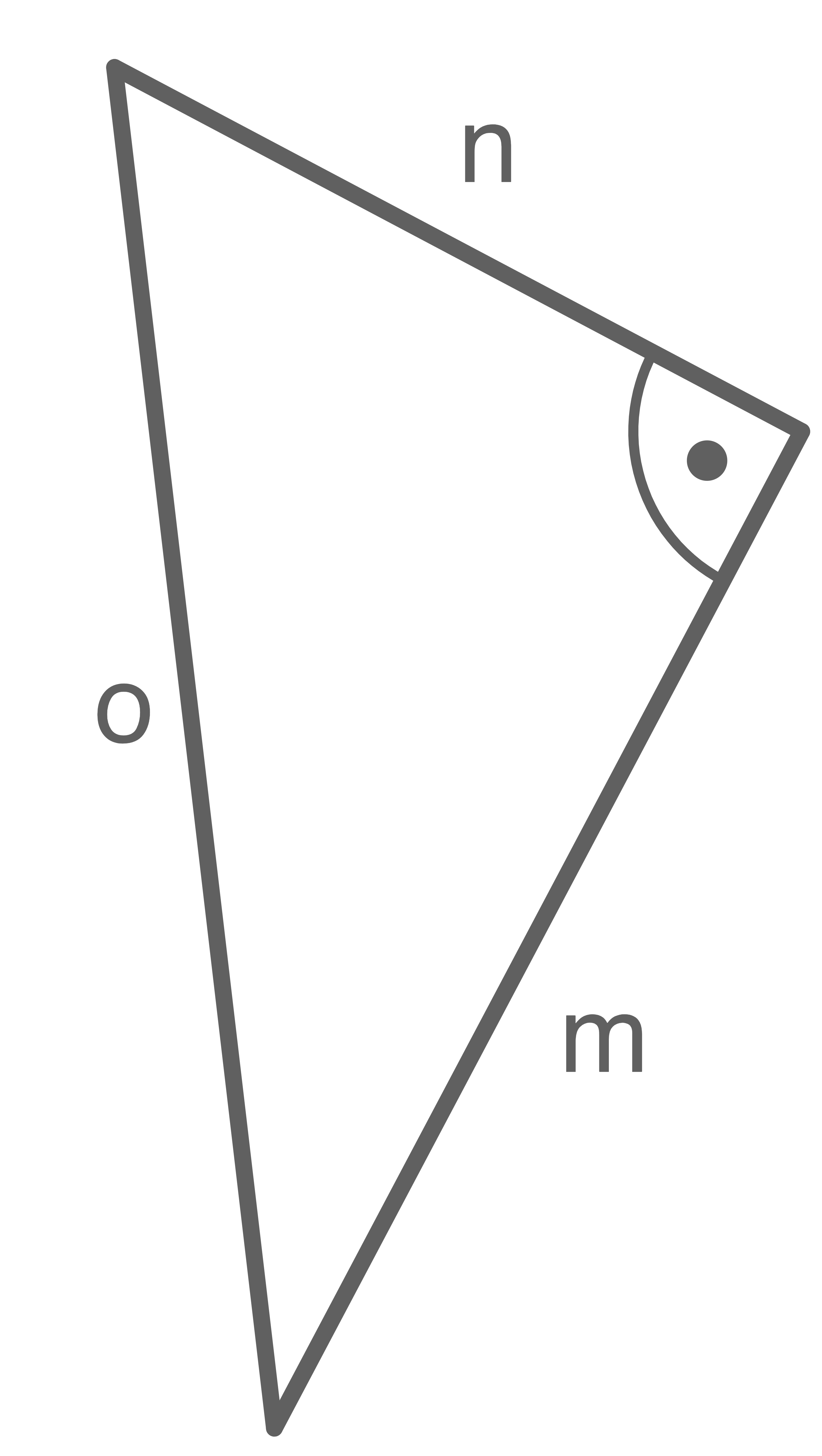
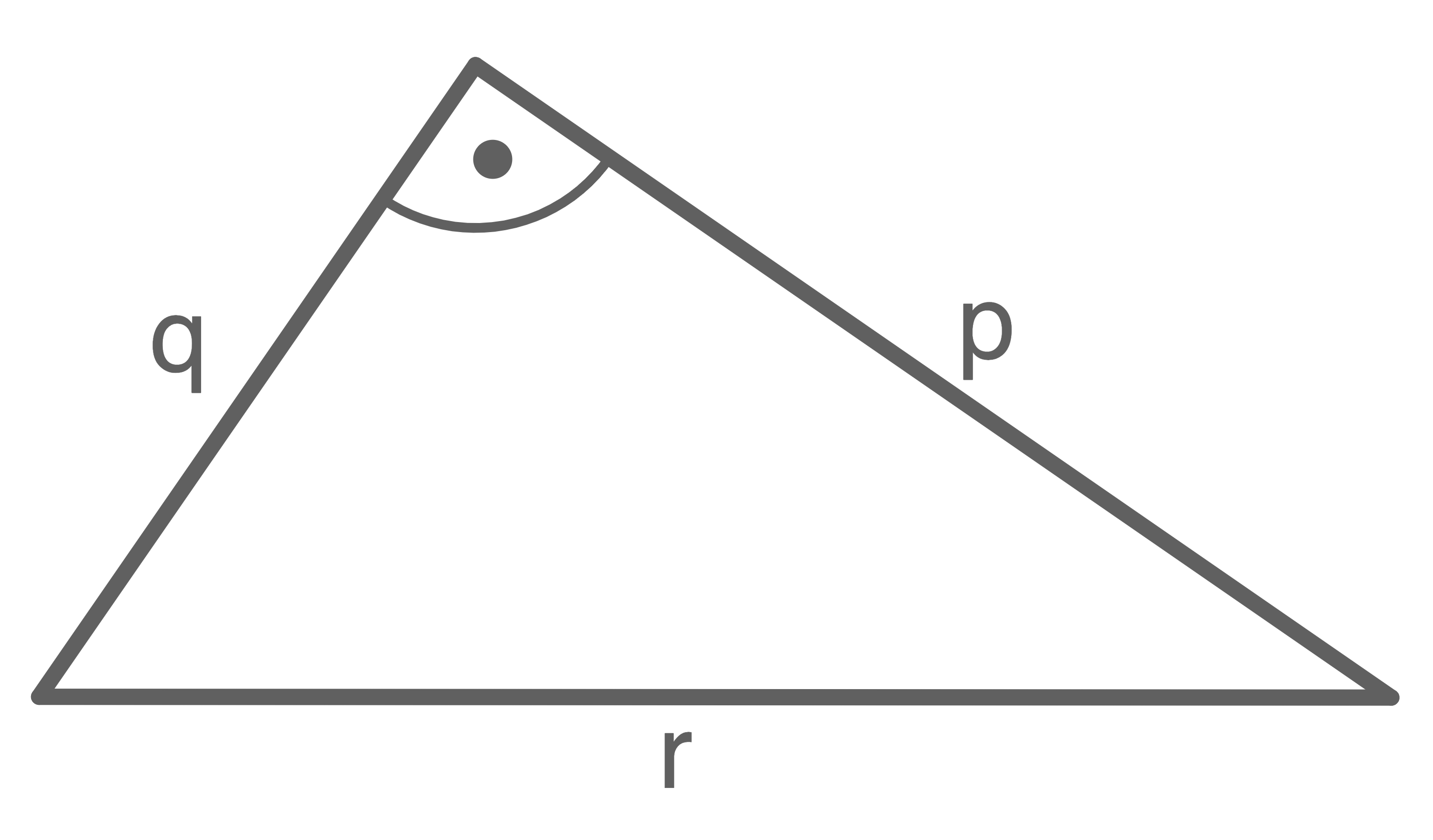
a)
b)
c)
d)
2
Es sind jeweils die Längen der beiden Katheten gegeben.
Berechne mit dem Satz des Pythagoras die Länge der Hypotenuse.
a)
b)
c)
d)
3
Es sind jeweils die Länge der Hypotenuse und die Länge einer Kathete gegeben.
Berechne mit dem Satz des Pythagoras die Länge der anderen Kathete.
a)
- Kathete:
- Hypothenuse:
b)
- Kathete:
- Hypothenuse:
c)
- Kathete:
- Hypothenuse:
d)
- Kathete:
- Hypothenuse:
4
Gegeben ist ein Dreieck mit 
und 
Ist das Dreieck rechtwinklig?
Begründe deine Antwort.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
d)
2
a)
b)
c)
d)
3
a)
b)
c)
d)
4
Falls das Dreieck rechtwinklig ist, gilt der Satz des Pythagoras.
In dem Fall muss gelten: 
und sind die beiden Katheten und 
die Hypothenuse. Denn die Hypotenuse muss immer die längste Seite sein.
![\(\begin{array}[t]{rll}
c^2&=&a^2+b^2 & \\[5pt]
c^2&=&(2,4\,\text{cm})^2+(5,2\,\text{cm})^2&\\[5pt]
c^2&=&5,76\,\text{cm}^2+27,04\,\text{cm}^2 &\\[5pt]
c^2&=& 32,8\,\text{cm}^2 &\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
c&\approx& 5,7\,\text{cm}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/2207882498735f5881511a27a193cd3664260f9f5fd4917ce0d5d19e7234ce62?color=5a5a5a)
Da für ein anderer Wert rauskommt als der, der in der Aufgabenstellung gegeben war, gilt: Das Dreieck ist nicht rechtwinklig.