Berechnungen an Dreiecken
Bei der Berechnung von Größen in Dreiecken hilft es, systematisch in einzelnen Schritten vorzugehen.
Rechtwinklige Dreiecke
Zunächst wird eine Skizze angefertigt, in welche die gegebenen und gesuchten Größen eingetragen und markiert werden.
Im zweiten Schritt wird zur Berechnung der gesuchten Größe eine der drei Gleichungen für Sinus, Kosinus und Tangens ausgesucht, in der die zwei gegebenen und die gesuchte Größe vorkommen.
Anschließend werden die gegebenen Größen in die Gleichung eingesetzt und nach der gesuchten Größe umgeformt, um diese zu berechnen.
Beispiel
Die Größe des Winkels  ist gesucht, somit wird dieser in der Skizze grün markiert:
ist gesucht, somit wird dieser in der Skizze grün markiert:
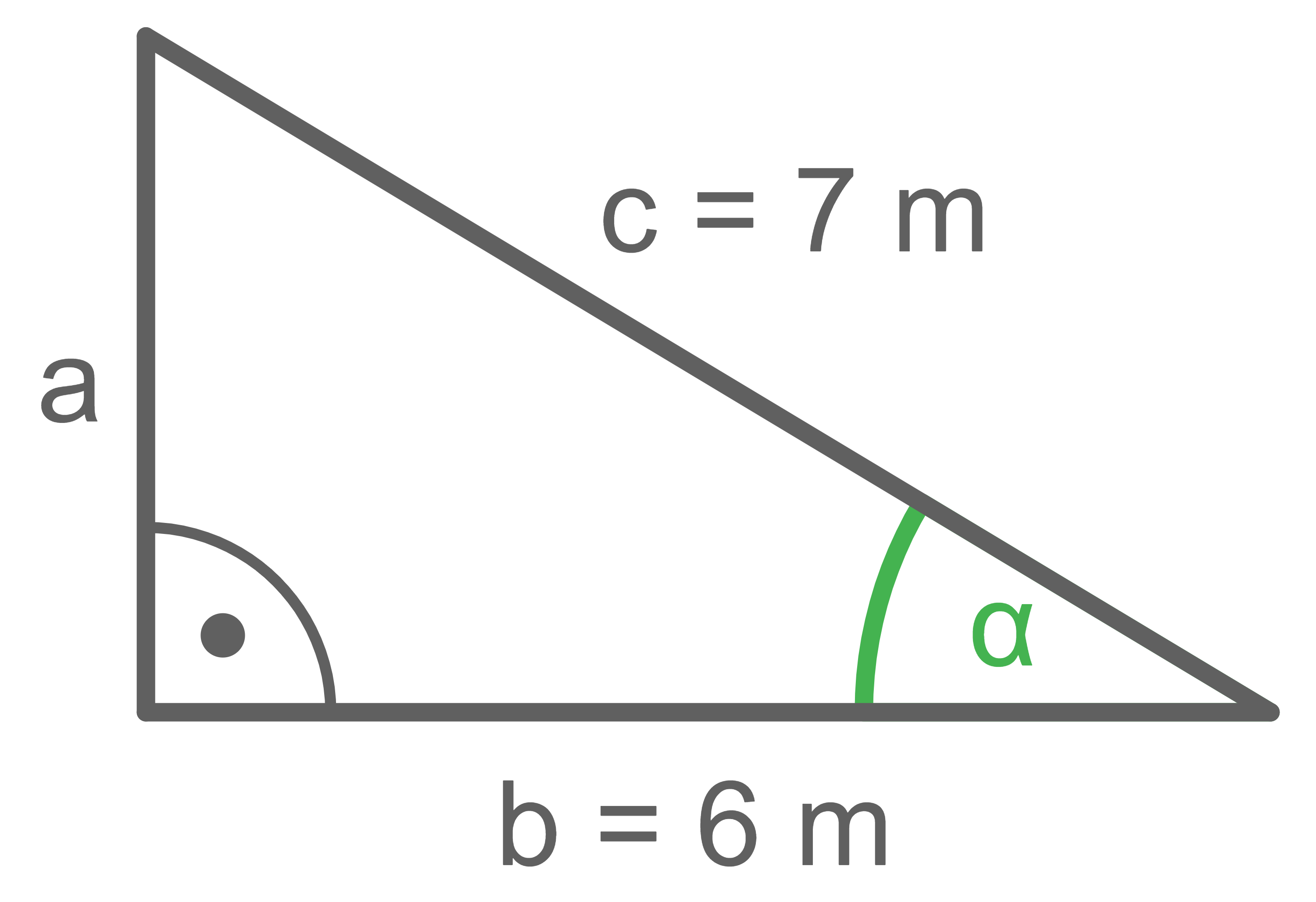 In diesem Fall sind die Ankathete und die Hypotenuse von
In diesem Fall sind die Ankathete und die Hypotenuse von  gegeben, das heißt der Kosinus wird verwendet:
gegeben, das heißt der Kosinus wird verwendet:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{b}{c} \\[5pt]
\cos(\alpha)&=&\dfrac{6\;\text{m}}{7\;\text{m}} &\quad \scriptsize \mid\;\cos^{-1} \\[5pt]
\alpha&\approx&31^\circ
\end{array}\)](https://mathjax.schullv.de/7926e81c97ef9efcef3bf45276d5657f61ef6ef266756f53b6c2537e35a15366?color=5a5a5a) Gleichschenklige Dreiecke
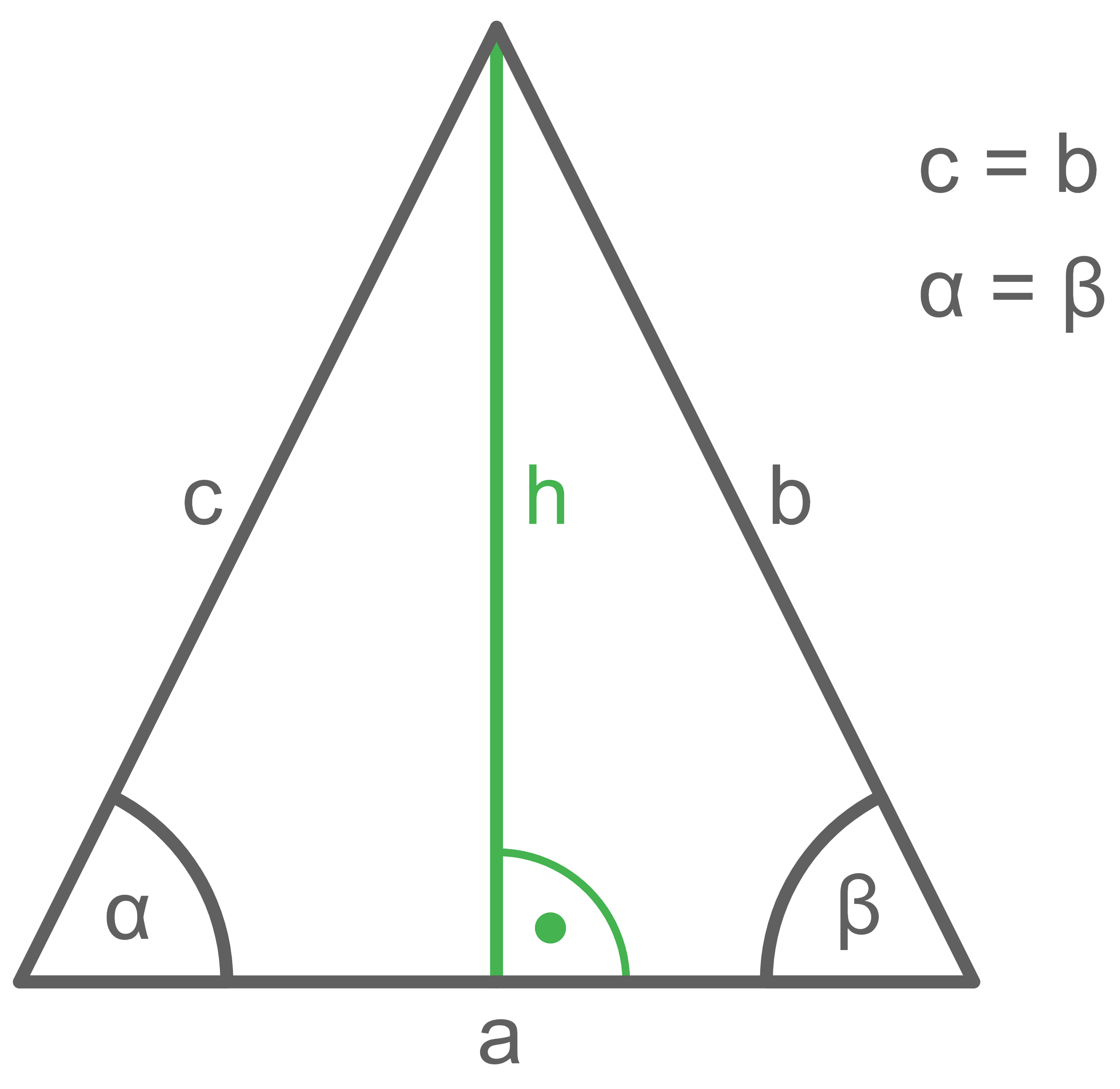
Auch hier wird als Erstes eine Skizze angefertigt.
Das eingezeichnete gleichschenklige Dreieck wird dann durch die Höhe in zwei kongruente rechtwinklige Dreiecke aufgeteilt.
Anschließend werden die restlichen der obigen Schritte für rechtwinklige Dreiecke auf die beiden entstandenen Teildreiecke angewendet. Hierbei kann auch die Winkelsumme der einzelnen Dreiecke helfen.
Skizze
Gleichschenklige Dreiecke
Auch hier wird als Erstes eine Skizze angefertigt.
Das eingezeichnete gleichschenklige Dreieck wird dann durch die Höhe in zwei kongruente rechtwinklige Dreiecke aufgeteilt.
Anschließend werden die restlichen der obigen Schritte für rechtwinklige Dreiecke auf die beiden entstandenen Teildreiecke angewendet. Hierbei kann auch die Winkelsumme der einzelnen Dreiecke helfen.
Skizze


1
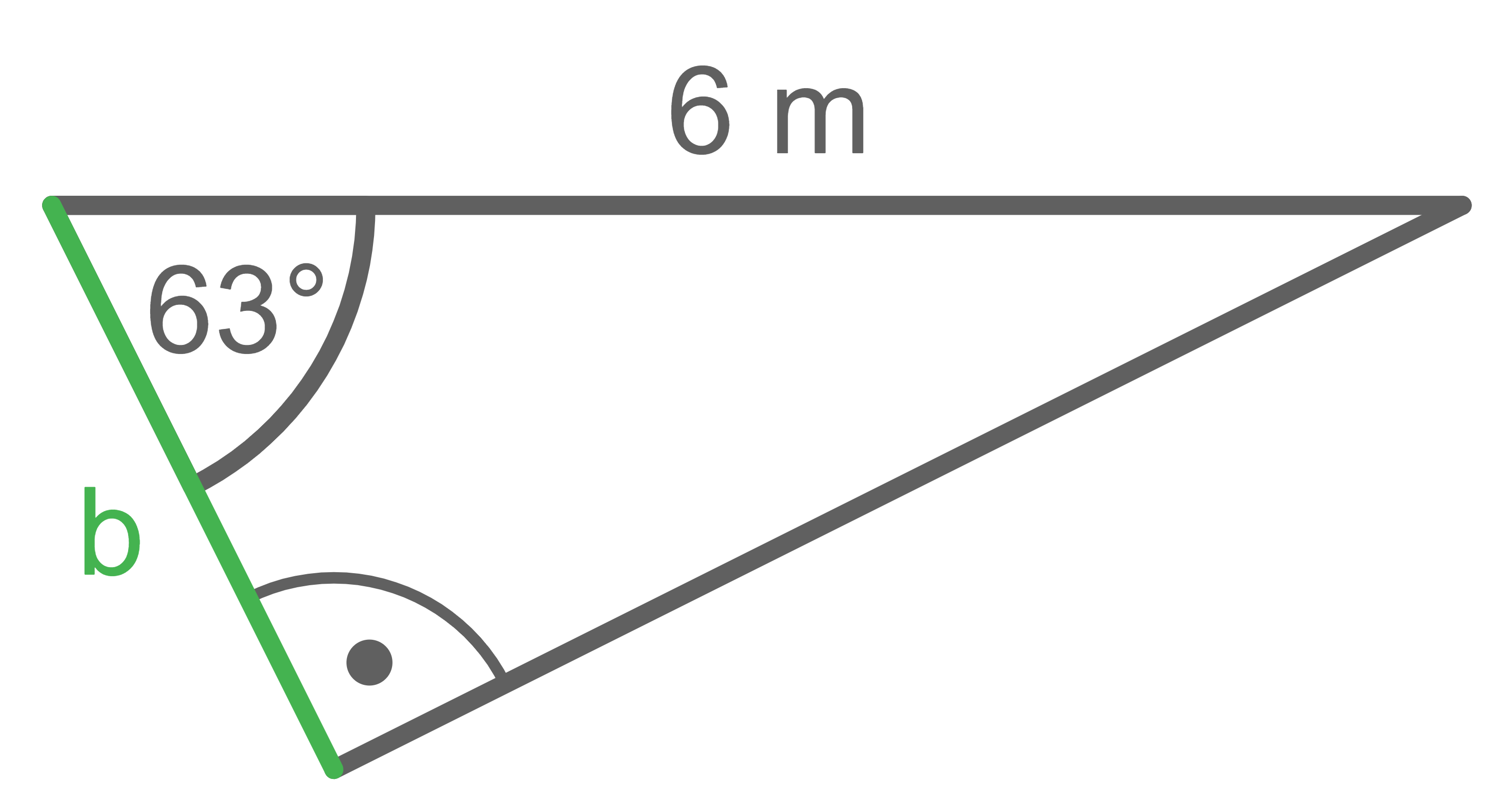
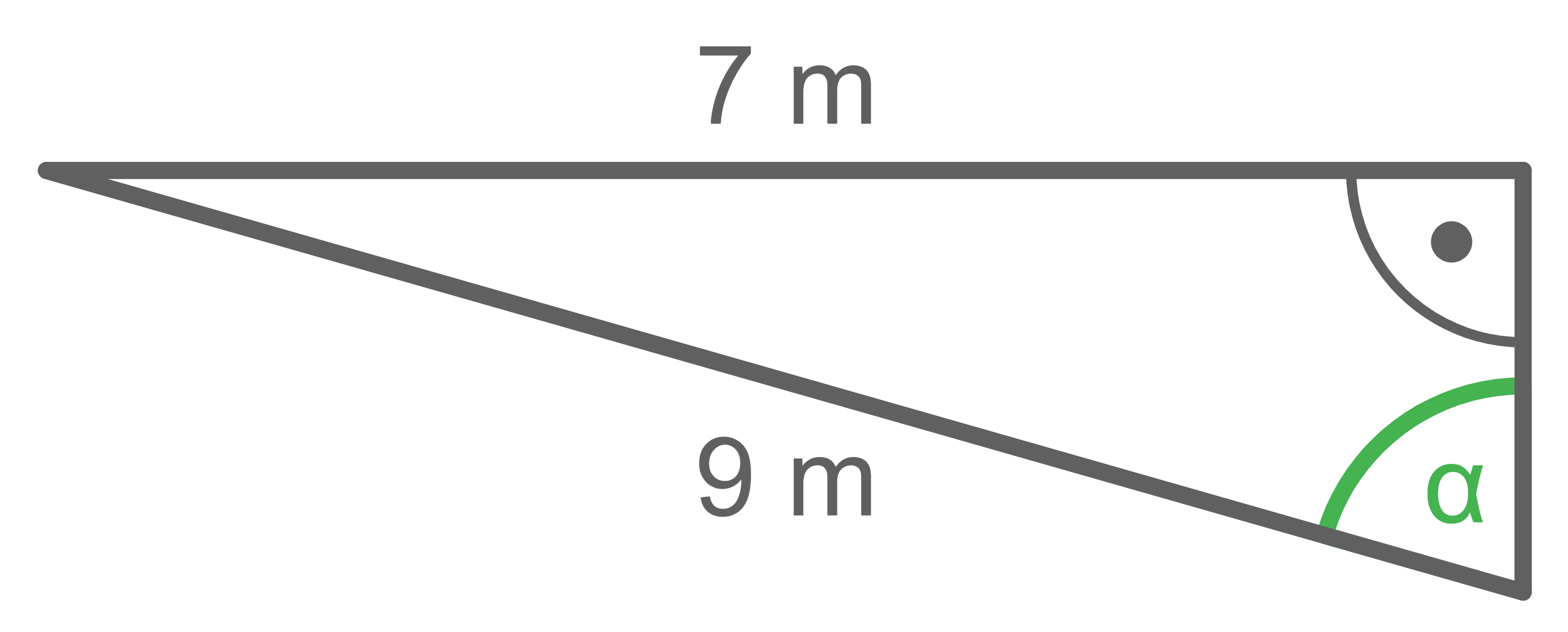
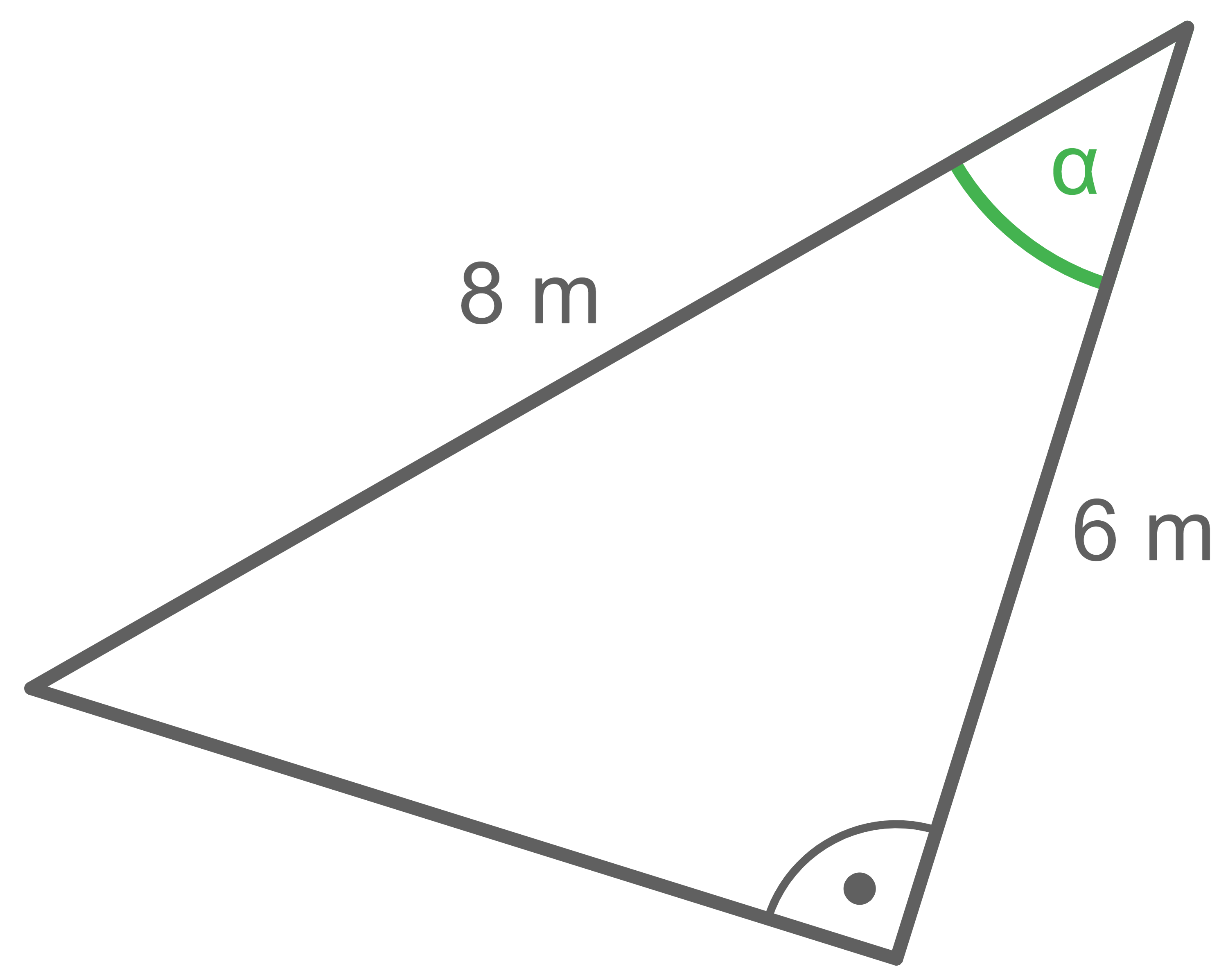
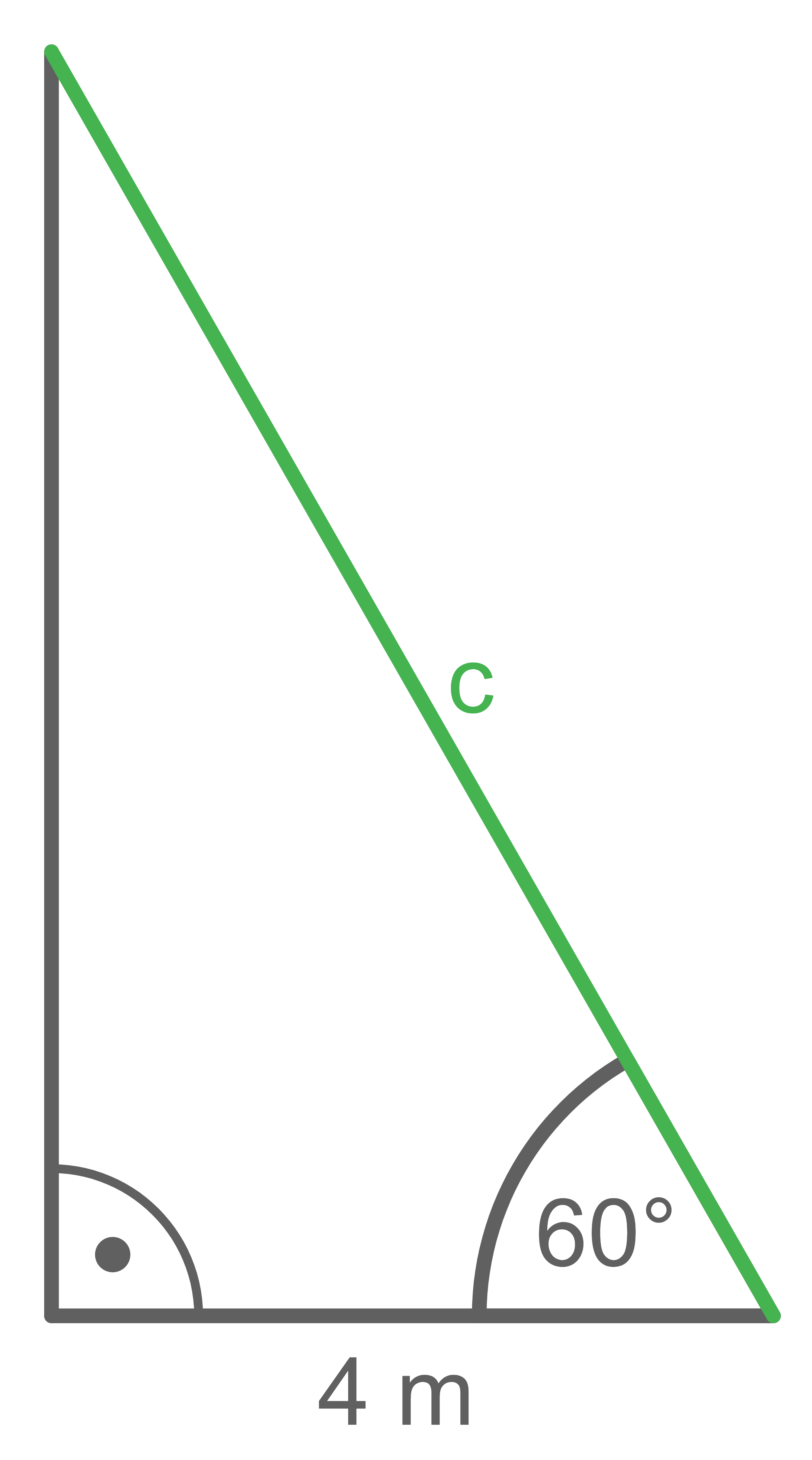
Berechne die in den Abbildungen jeweils grün markierte Größe.
a)

b)

c)

d)

2
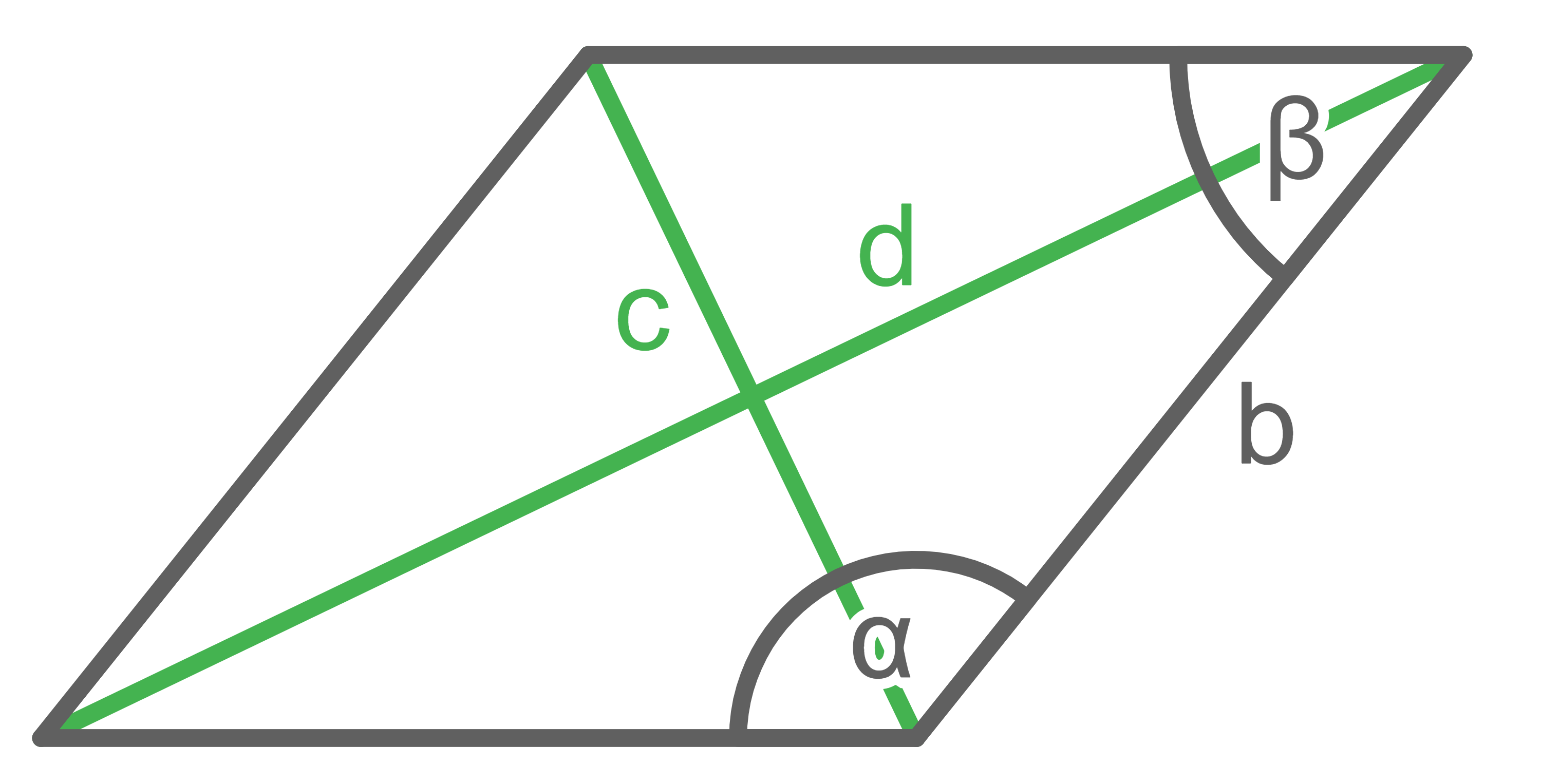
Von der abgebildeten Raute sind die Längen der grün markierten Diagonalen  und
und  bekannt, sie betragen
bekannt, sie betragen  und
und 
Berechne die eingezeichneten Winkel und
und  sowie den Wert von
sowie den Wert von 
Berechne die eingezeichneten Winkel
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Ankathete:  Hypotenuse:
Hypotenuse: 
 Mit dem Kosinus folgt:
Mit dem Kosinus folgt:
![\(\begin{array}[t]{rll}
\dfrac{b}{6}&=&\cos(63^\circ) &\quad \scriptsize \mid\;\cdot 6 \\[5pt]
b&=&6\cdot\cos(63^\circ) \\[5pt]
b&\approx&2,72\;[\text{m}]
\end{array}\)](https://mathjax.schullv.de/5ef14a5a61741890ea522c049431bcd53bdb824c7f2a2705fbb04807b878523f?color=5a5a5a)
b)
Gegenkathete:  Hypotenuse:
Hypotenuse:  Der Sinus liefert:
Der Sinus liefert:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{7}{9} &\quad \scriptsize \mid\;\sin^{-1} \\[5pt]
\alpha&=&\sin^{-1}\left(\dfrac{7}{9}\right) \\[5pt]
\alpha&\approx&51,06^\circ
\end{array}\)](https://mathjax.schullv.de/f0f62da6a673d168e002c4803b7a951ca9f0bf53c890e9215b40ec95778aa5af?color=5a5a5a)
c)
Ankathete:  Hypotenuse:
Hypotenuse:  Mit dem Kosinus folgt:
Mit dem Kosinus folgt:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{6}{8} &\quad \scriptsize \mid\;\cos^{-1} \\[5pt]
\alpha&=&\cos^{-1}\left(\dfrac{6}{8}\right) \\[5pt]
\alpha&\approx&41,41^\circ
\end{array}\)](https://mathjax.schullv.de/05476224699304180ddf148b36d744f19037eef4df7d9220024cfc51ba9e3470?color=5a5a5a)
d)
Ankathete:  Hypotenuse:
Hypotenuse: 
 Der Kosinus liefert:
Der Kosinus liefert:
![\(\begin{array}[t]{rll}
\cos(60^\circ)&=&\dfrac{4}{c} &\quad \scriptsize \mid\;\cdot c \\[5pt]
c\cdot\cos(60^\circ)&=&4 &\quad \scriptsize \mid\;:\cos(60^\circ) \\[5pt]
c&=&\dfrac{4}{\cos(60^\circ)} \\[5pt]
c&=&8\;[\text{m}]
\end{array}\)](https://mathjax.schullv.de/804400a854a1904f47f247d24eb803c53978566f9f029e5cca7d19496f485b13?color=5a5a5a)
2
Da es sich um eine Raute handelt, sind alle vier Seiten gleich lang. Somit lässt sich die Raute entlang der beiden Diagonalen in vier kongruente rechtwinklige Dreiecke teilen:
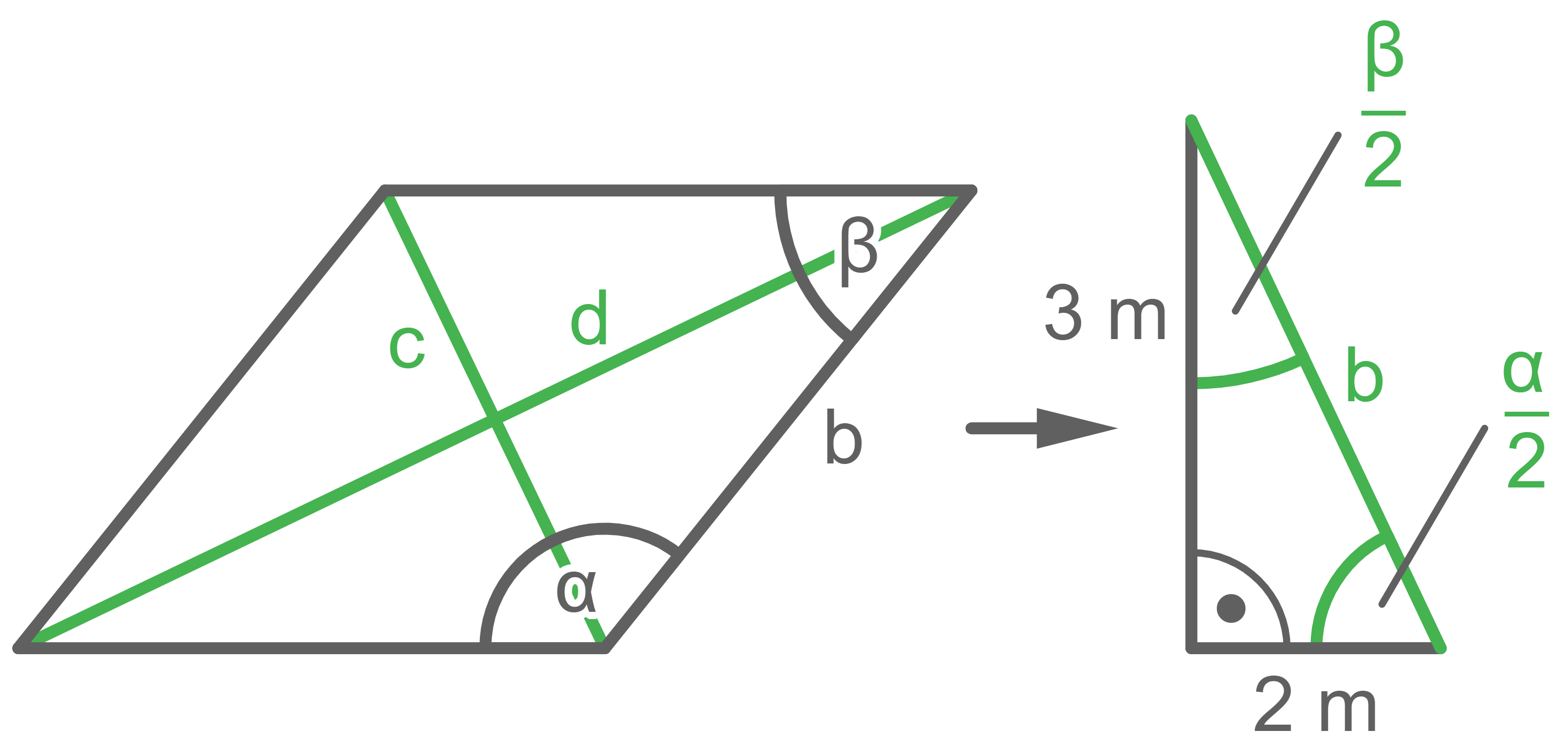 Anhand der Skizze wird erkenntlich, dass ein Dreieck mit Seitenlängen
Anhand der Skizze wird erkenntlich, dass ein Dreieck mit Seitenlängen  und
und  sowie Winkeln
sowie Winkeln  und
und  entsteht. Für den Winkel
entsteht. Für den Winkel  sind die Werte der Ankathete und der Gegenkathete bekannt, somit folgt mit dem Tangens:
sind die Werte der Ankathete und der Gegenkathete bekannt, somit folgt mit dem Tangens:
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\alpha}{2}\right)&=&\dfrac{3}{2} &\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\dfrac{\alpha}{2}&=&\tan^{-1}\left(\dfrac{3}{2}\right) &\quad \scriptsize \mid\;\cdot2 \\[5pt]
\alpha&=&2\cdot\tan^{-1}\left(\dfrac{3}{2}\right) \\[5pt]
\alpha&\approx&112,62^\circ
\end{array}\)](https://mathjax.schullv.de/1bd9e2dab4f8fe8a14a6f2e8e70fc88184c3b85f13110bf96a7f28a6eb899c5a?color=5a5a5a) Für den Winkel
Für den Winkel  beschreibt
beschreibt  den Wert der Ankathete und
den Wert der Ankathete und  den Wert der Gegenkathete. Der Tangens liefert daher:
den Wert der Gegenkathete. Der Tangens liefert daher:
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\beta}{2}\right)&=&\dfrac{2}{3} &\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\dfrac{\beta}{2}&=&\tan^{-1}\left(\dfrac{2}{3}\right) &\quad \scriptsize \mid\;\cdot2 \\[5pt]
\beta&=&2\cdot\tan^{-1}\left(\dfrac{2}{3}\right) \\[5pt]
\beta&\approx&67,38^\circ
\end{array}\)](https://mathjax.schullv.de/ec3a6232b8c05d2934bc501bee1ea614ae01b1625f36eb2a954de1620dd1e1e1?color=5a5a5a) Mit Hilfe z.B. des Werts von
Mit Hilfe z.B. des Werts von  kann nun der Wert von
kann nun der Wert von  berechnet werden. Die Seite
berechnet werden. Die Seite  ist die Hypotenuse des Dreiecks, zudem ist z.B. die Ankathete
ist die Hypotenuse des Dreiecks, zudem ist z.B. die Ankathete  des Winkels
des Winkels  gegeben. Mit dem Kosinus folgt somit:
gegeben. Mit dem Kosinus folgt somit:
