Satz des Pythagoras im Raum
Passende rechtwinklige Dreiecke helfen in Körpern, Streckenlängen zu berechnen. Dazu kann der Satz des Pythagoras angewendet werden.
 berechnet werden.
berechnet werden.
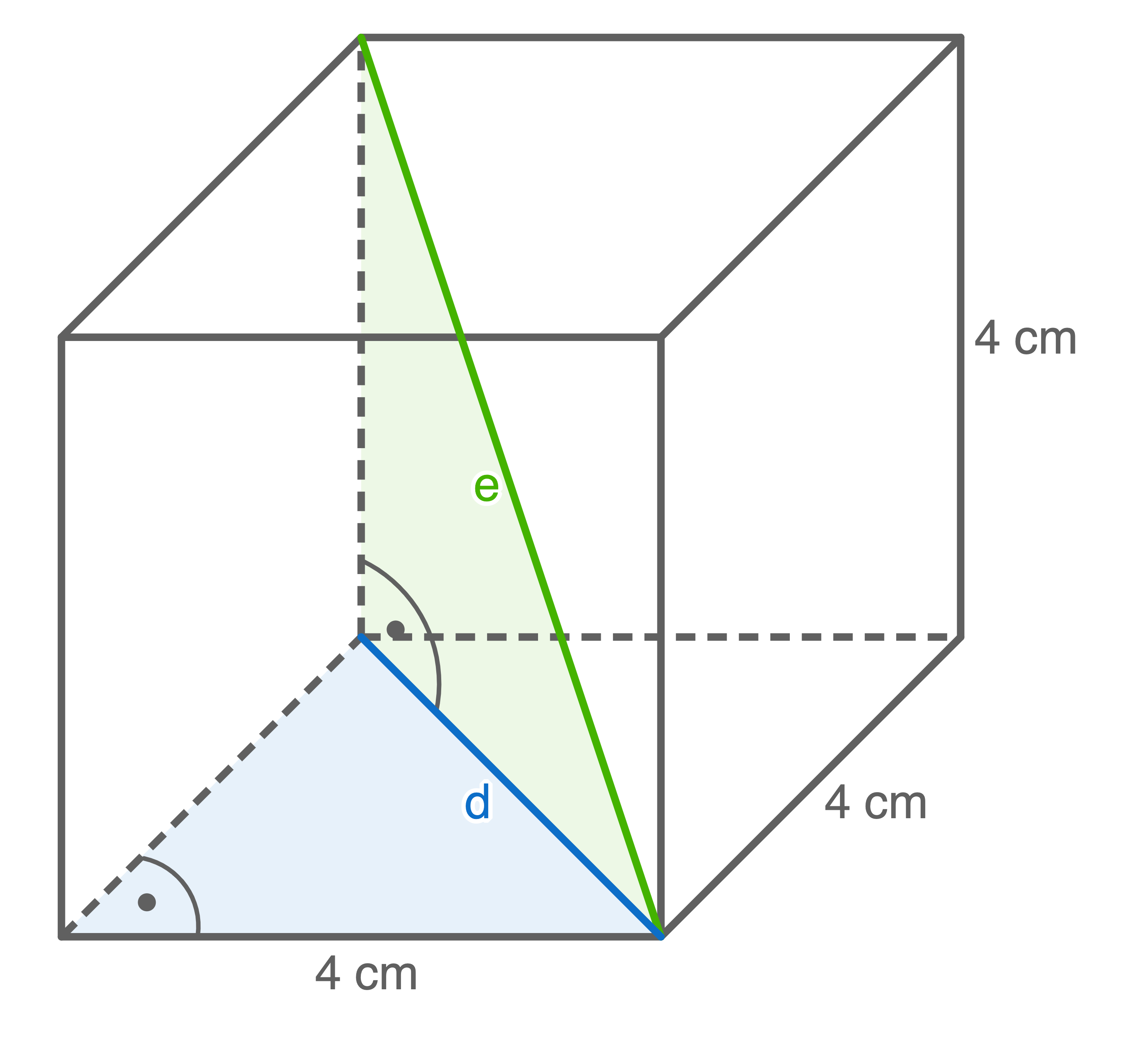
Beispiel
Im Würfel soll die Länge der Raumdiagonalen
1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
d^2&=&(4\,\text{cm})^2+(4\,\text{cm})^2 \quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
d&=&\sqrt{(4\,\text{cm})^2+(4\,\text{cm})^2} \\[5pt]
d&=&5,7\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/a005f09c288b583dd820157f22f9ccad5c0c6c3672583d1d296d7f87e881428a?color=5a5a5a) 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
e^2&=&(4\,\text{cm})^2+(5,7\,\text{cm})^2 \quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
e&=&\sqrt{(4\,\text{cm})^2+(5,7\,\text{cm})^2} \\[5pt]
e&=&7\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/1ed061207fa00cf9aee00a26213eea95702a2bda2b4e1722d8bf1cc5f1171a6f?color=5a5a5a)
1
Berechne die Länge der markierten Raum- und Flächendiagonalen.
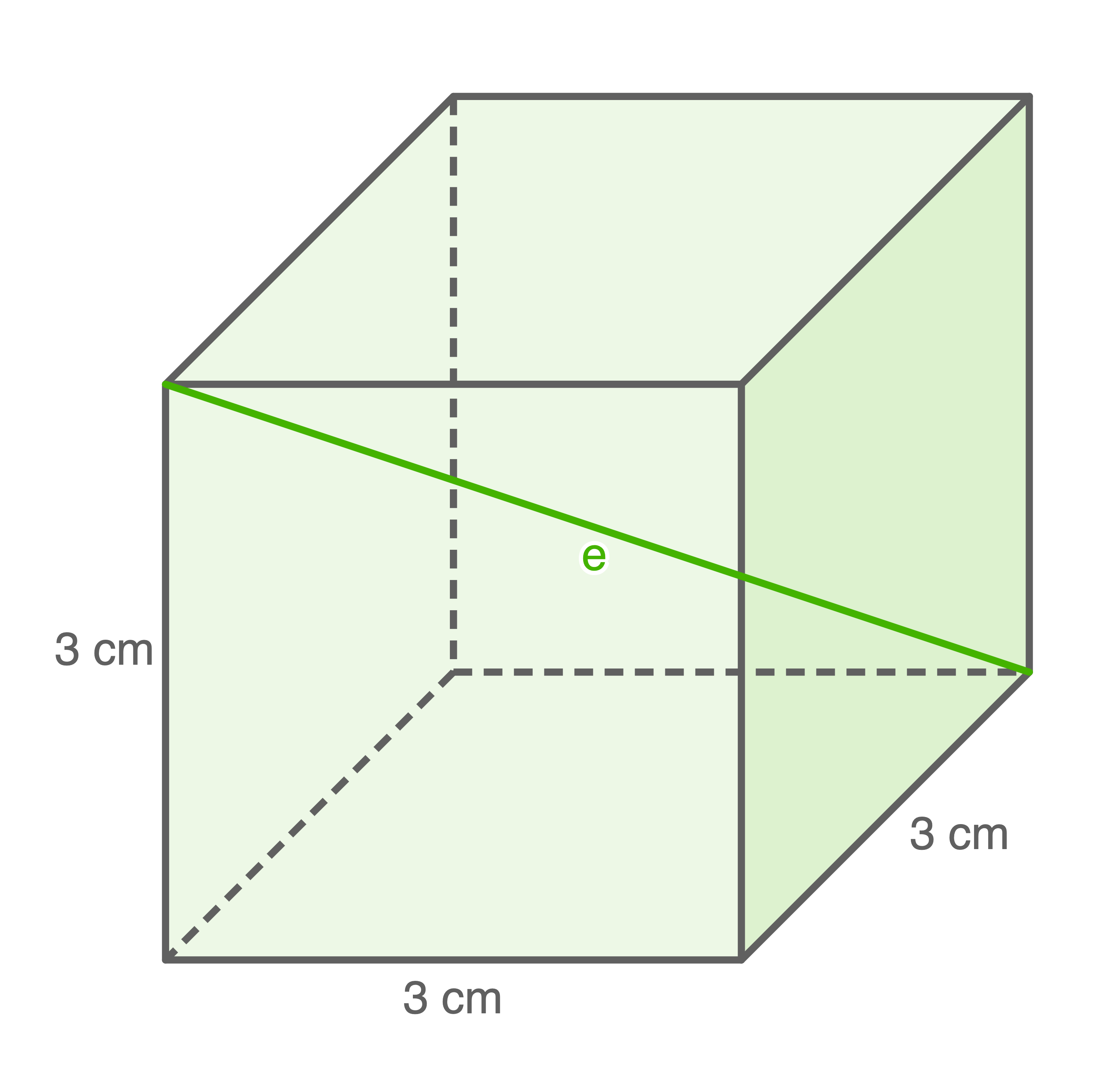
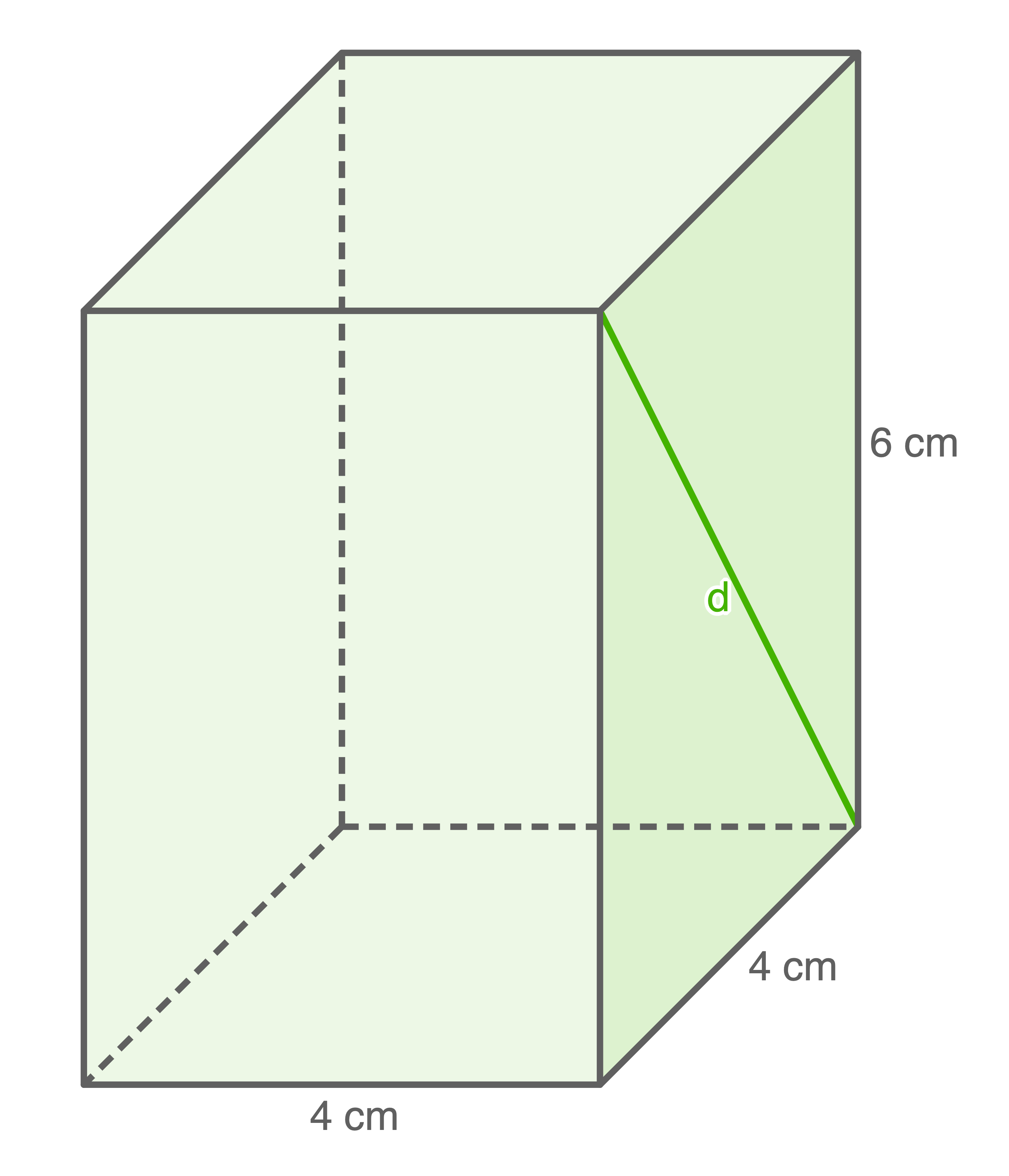
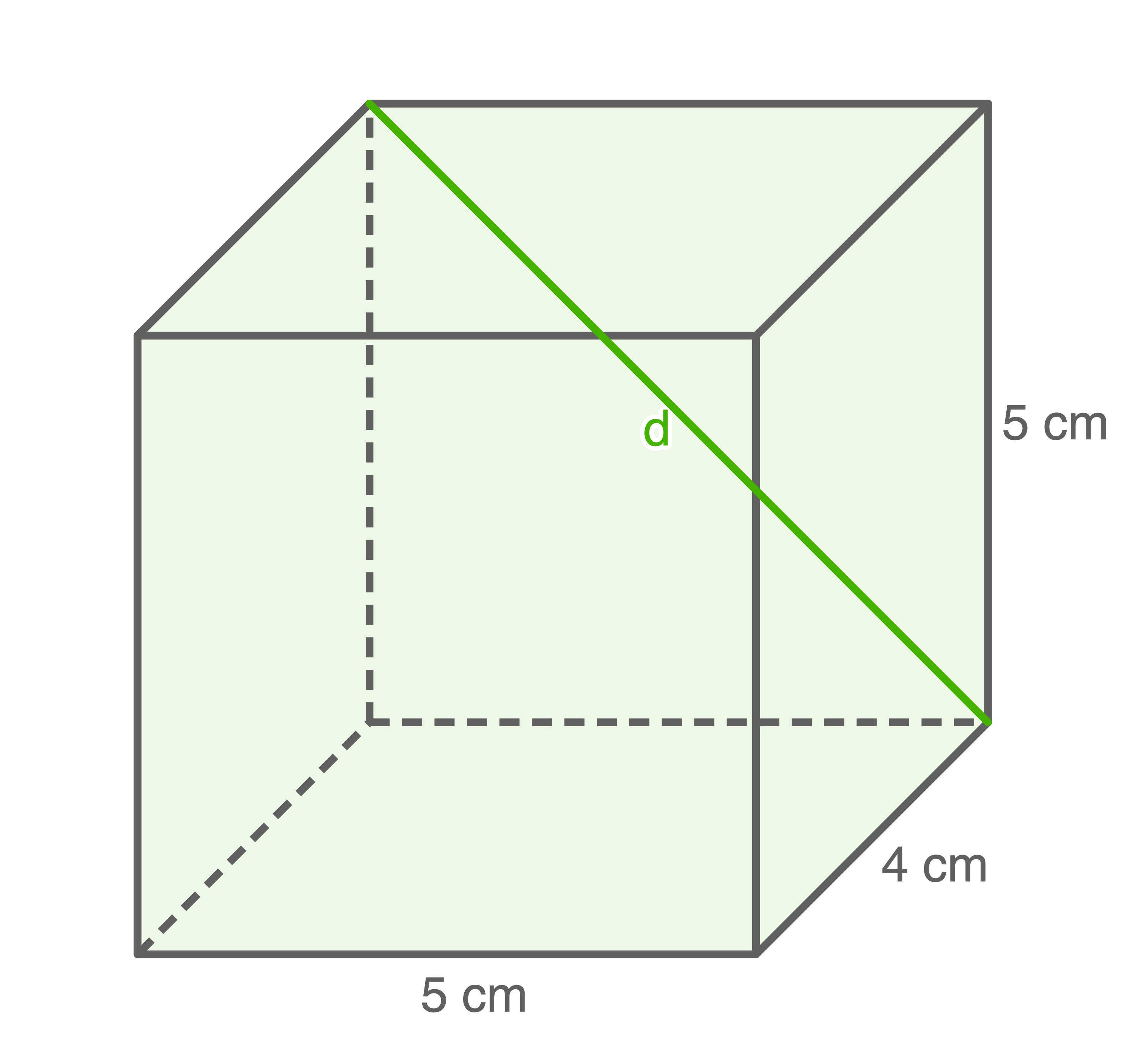
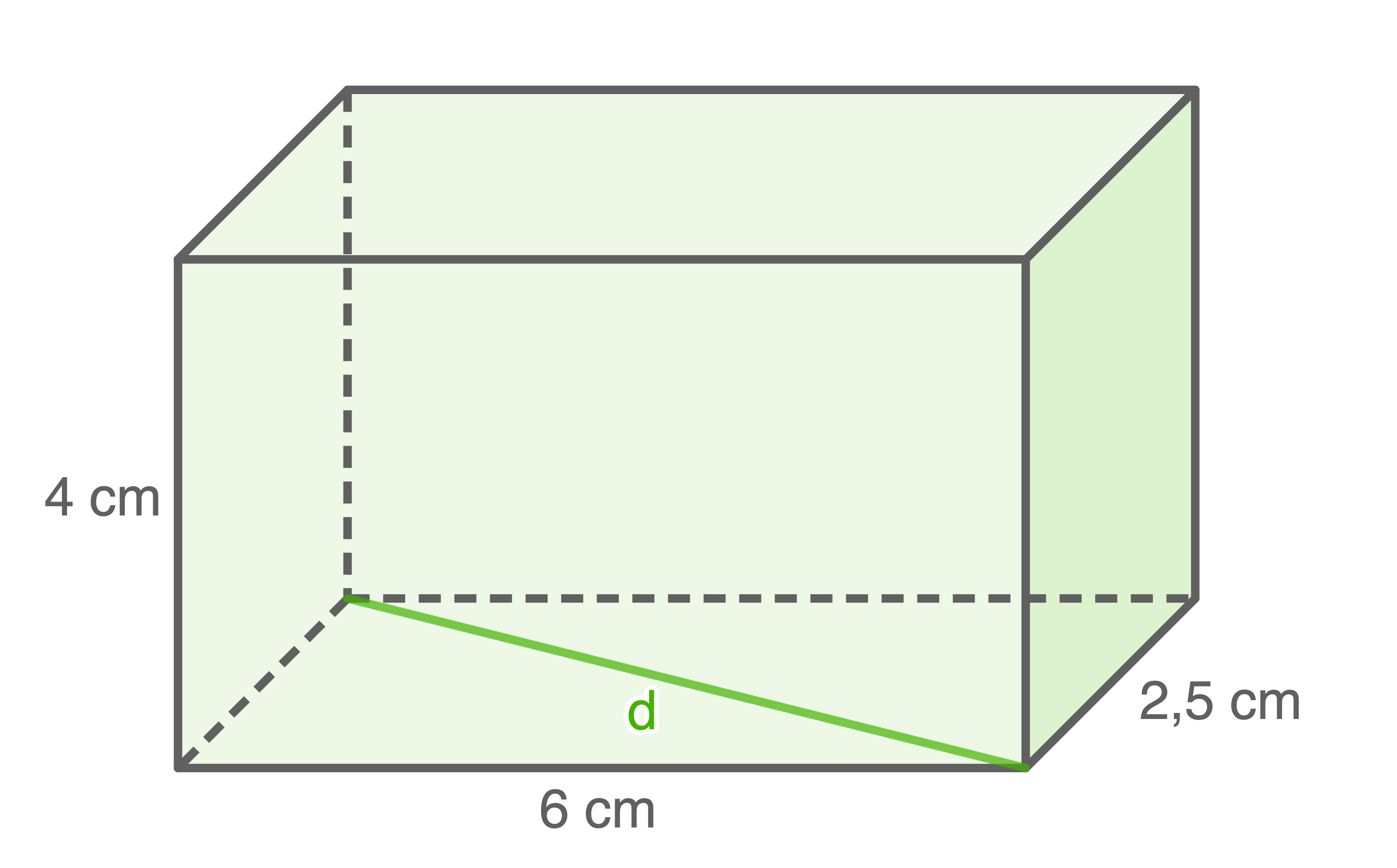
a)

b)

c)

d)

2
Berechne die Länge der Strecke 
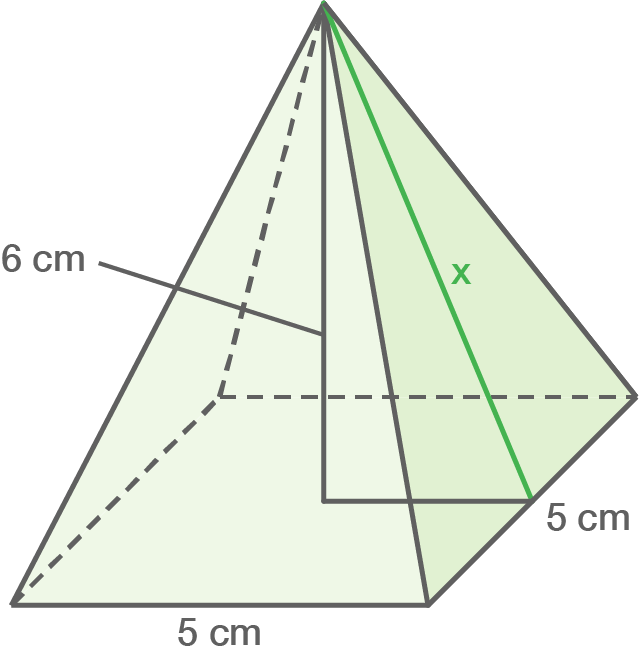
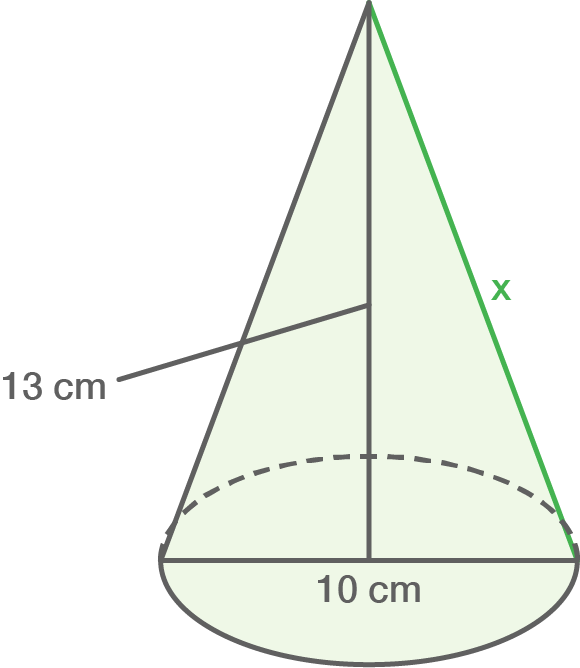
a)

b)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
d)
2
a)
b)