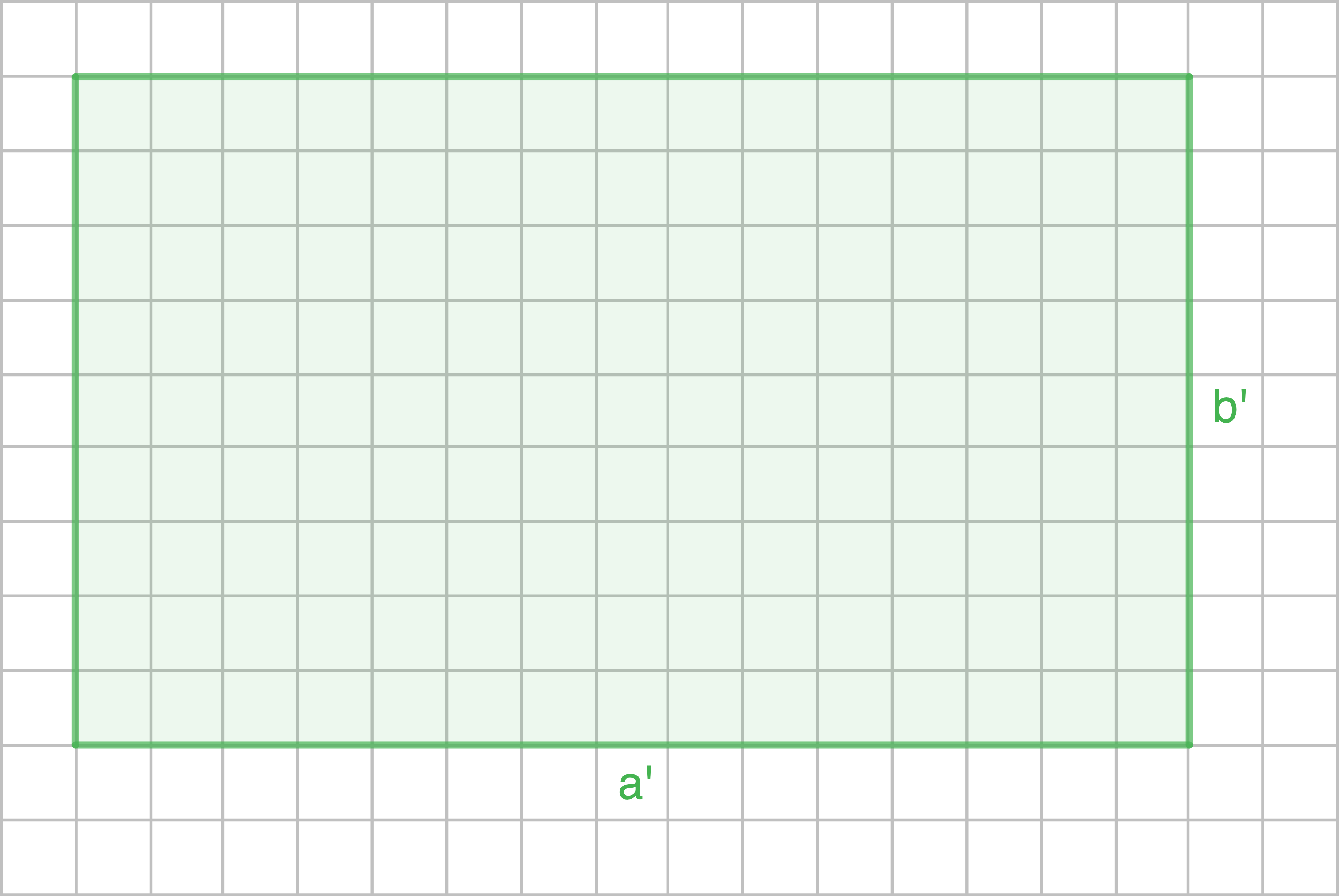
Ähnliche Figuren
Wird eine Figur vergrößert oder verkleinert, entsteht eine neue Figur. Diese Figur wird ähnliche Figur genannt.
Beispiel
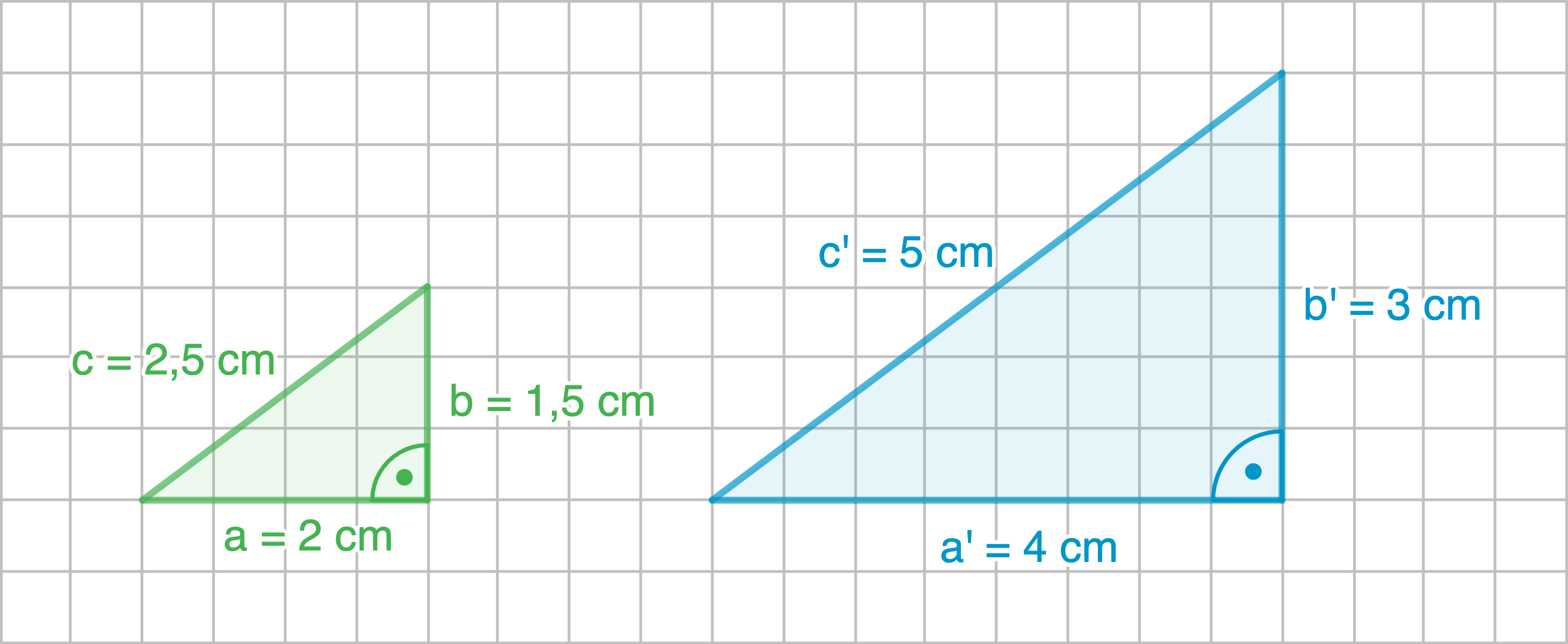
Längenverhältnis 1
Längenverhältnis 2
Längenverhältnis 3
Die Dreiecke sind ähnlich.
- Seiten, die zusammengehören, haben die gleichen Längenverhältnisse. Sie entsprechen dem Faktor
- Winkel, die zusammengehören, sind gleich groß.
Längenverhältnis 1
- Die Längenverhältnisse aller zusammengehörenden Seiten sind gleich und entsprechen dem Faktor
- Zudem sind die Winkel gleich groß.
1
Sind die Figuren ähnlich? Begründe.
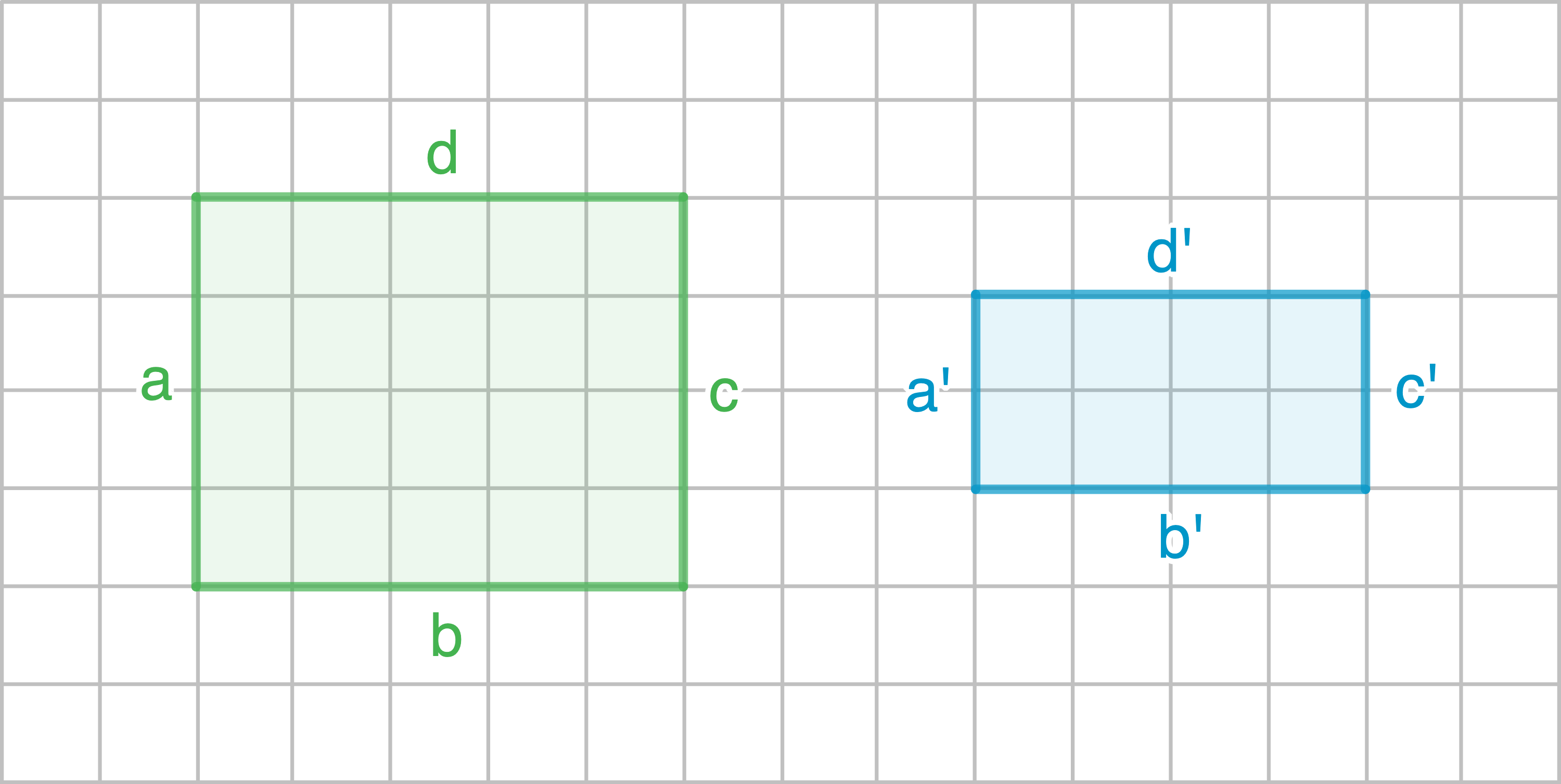
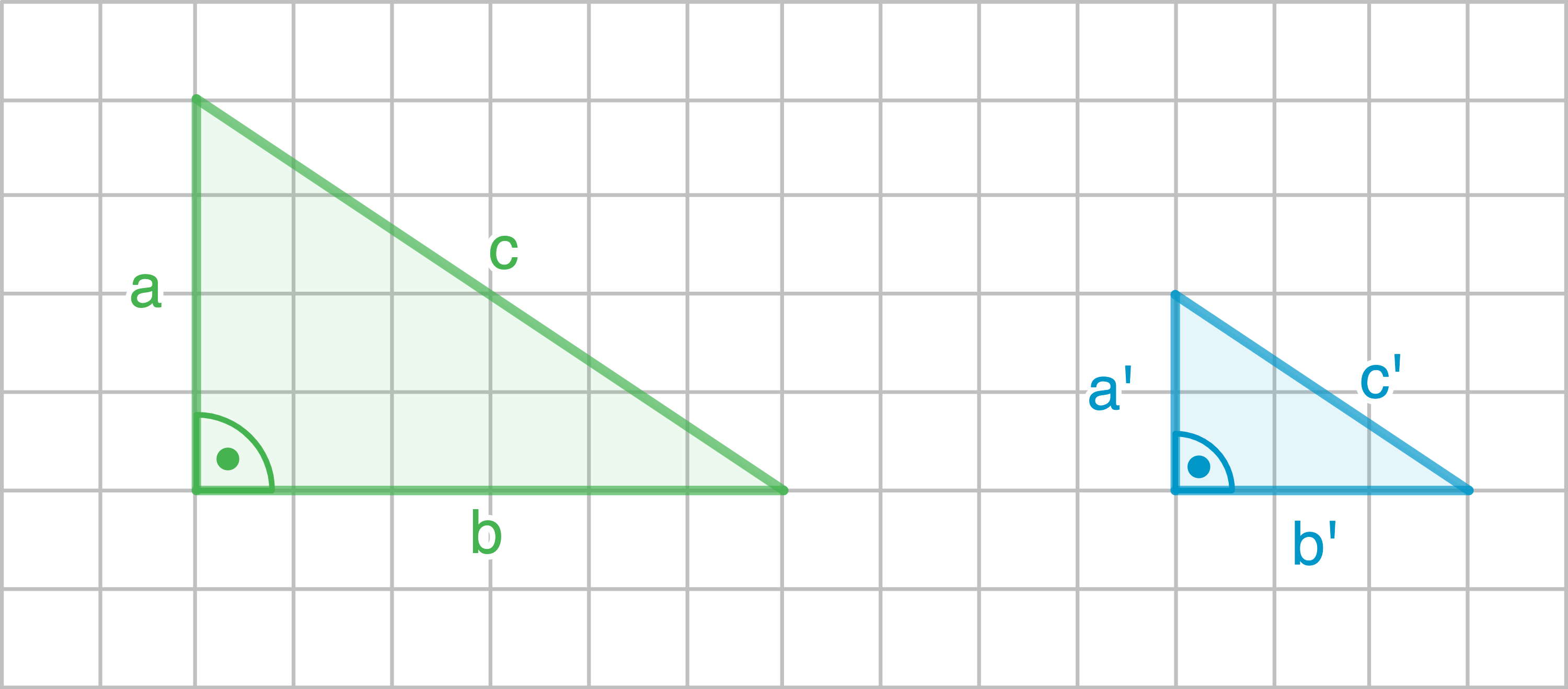
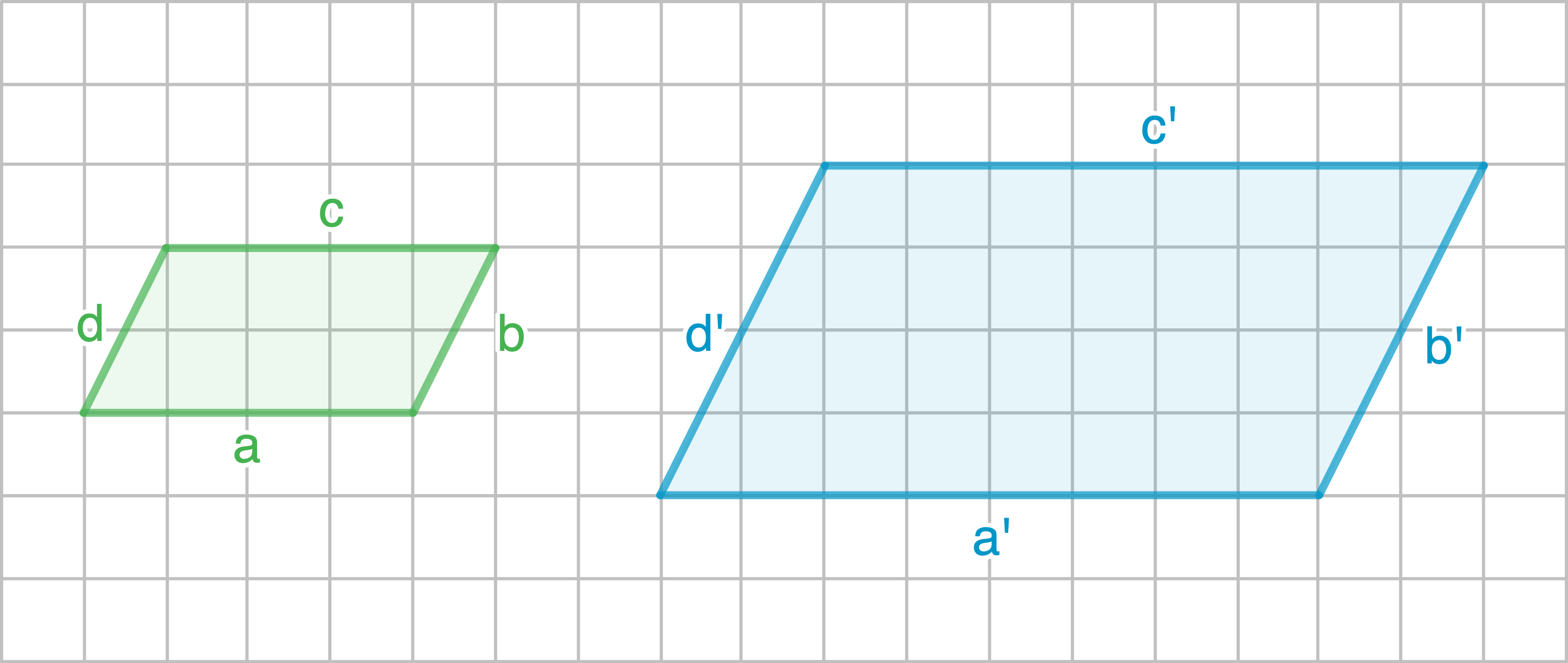
a)
b)
c)
2
Für ein Rechteck 
gilt:
Davon ist bereits gegeben:
a)
Bestimme den Faktor 
b)
Zeichne das ähnliche Rechteck
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Längenverhältnis 1
Längenverhältnis 2
Die Längenverhältnisse stimmen nicht überein.
Die Rechtecke sind nicht ähnlich.
b)
Längenverhältnis 1
Längenverhältnis 2
Um das Längenverhältnis 3 bestimmen zu können, muss zunächst die Längen der Seite 
und der Seite 
mit dem Satz des Pythagoras berechnet werden.
![\(\begin{array}[t]{rll}
c^2&=&a^2+b^2 &\\[5pt]
c^2&=&2^2+3^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
c&=&\sqrt{2^2+3^2} &\\[5pt]
c&=&3,6 &\\[5pt]
\end{array}\)](https://mathjax.schullv.de/f78b94f3be81300b1d260d54c4901fe87221dd9c8838b2724a51bbc1dd4f59c1?color=5a5a5a)
![\(\begin{array}[t]{rll}
c](https://mathjax.schullv.de/7f0233e96c5450a42281ce3a3918313eab195b7586759a224e2d19bc5c7cc5b9?color=5a5a5a)
Längenverhältnis 3
Die Längenverhältnisse stimmen überein.
Somit gilt: 
Die Rechtecke sind ähnlich.
c)
Längenverhältnis 1
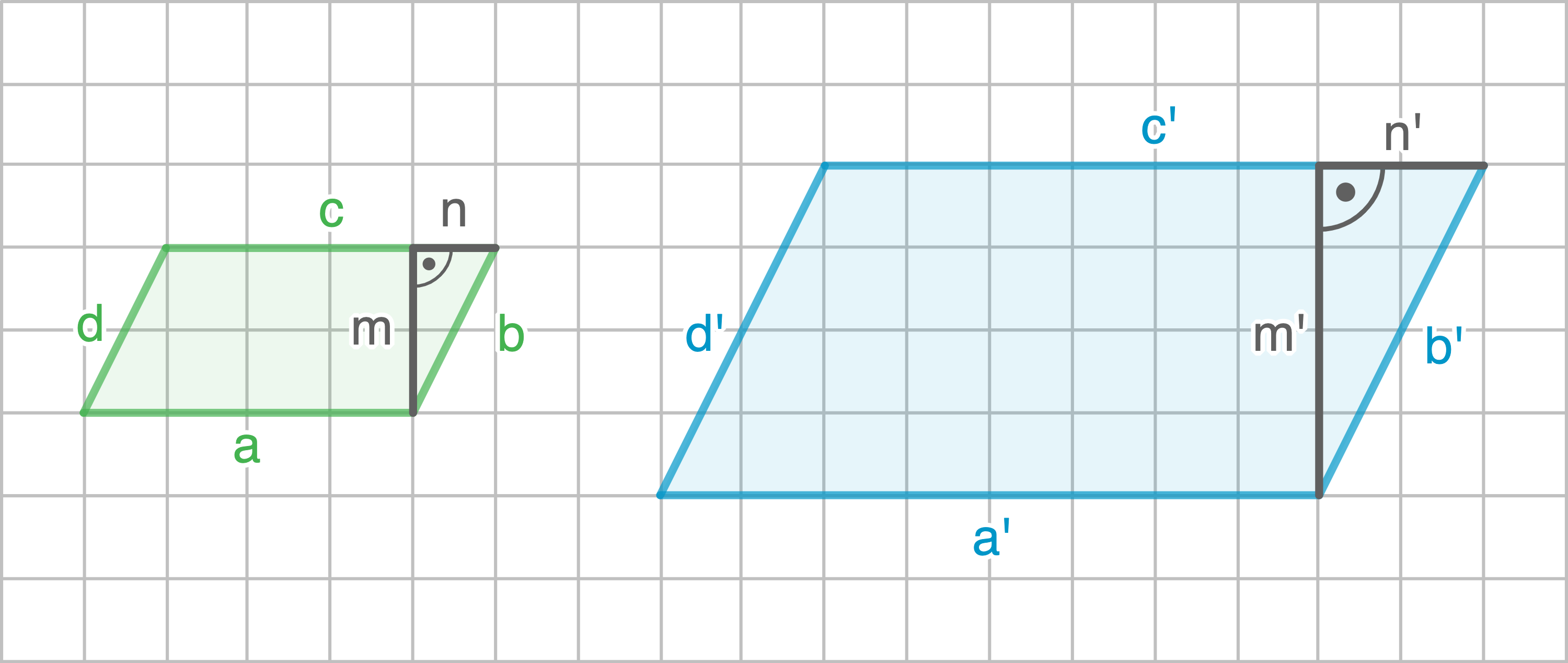Um das Längenverhältnis 2 bestimmen zu können, muss zunächst die Länge der Seite 
und der Seite 
mit dem Satz des Pythagoras berechnet werden.
![\(\begin{array}[t]{rll}
b^2&=&m^2+n^2 &\\[5pt]
b^2&=&1^2+0,5^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
b&=&\sqrt{1^2+0,5^2} &\\[5pt]
b&=&1,1
\end{array}\)](https://mathjax.schullv.de/c1f4bff94c02fd6bccd94b5465908da764ff6f30c324b4ce0085730dc0d41d64?color=5a5a5a)
![\(\begin{array}[t]{rll}
b](https://mathjax.schullv.de/e7ef967b74a57649ec107260fec44cb5e2b01a68777a6ba44afd95c4772ff119?color=5a5a5a)
Längenverhältnis 3
Die Längenverhältnisse stimmen überein.
Somit gilt: 
Die Parallelogramme sind ähnlich.
2
a)
Da das Rechteck 
ähnlich zu Rechteck ist, gilt: 
Längenverhältnis 1
Somit gilt für den Faktor: 
b)
Länge der Seite berechnen:
