Schnittpunkte
Die Schnittpunkte zweier Graphen können zeichnerisch oder rechnerisch ermittelt werden.
Um die Koordinaten der Schnittpunkte zu berechnen, werden die Funktionsterme gleichgesetzt.
Zwei Parabeln können keinen, einen oder zwei Schnittpunkt(e) haben.
Eine Parabel und eine Gerade können ebenfalls keinen, einen oder zwei Schnittpunkt(e) haben.
Haben eine Gerade und eine Parabel nur einen gemeinsamen Schnittpunkt, heißt dieser auch Berührpunkt.
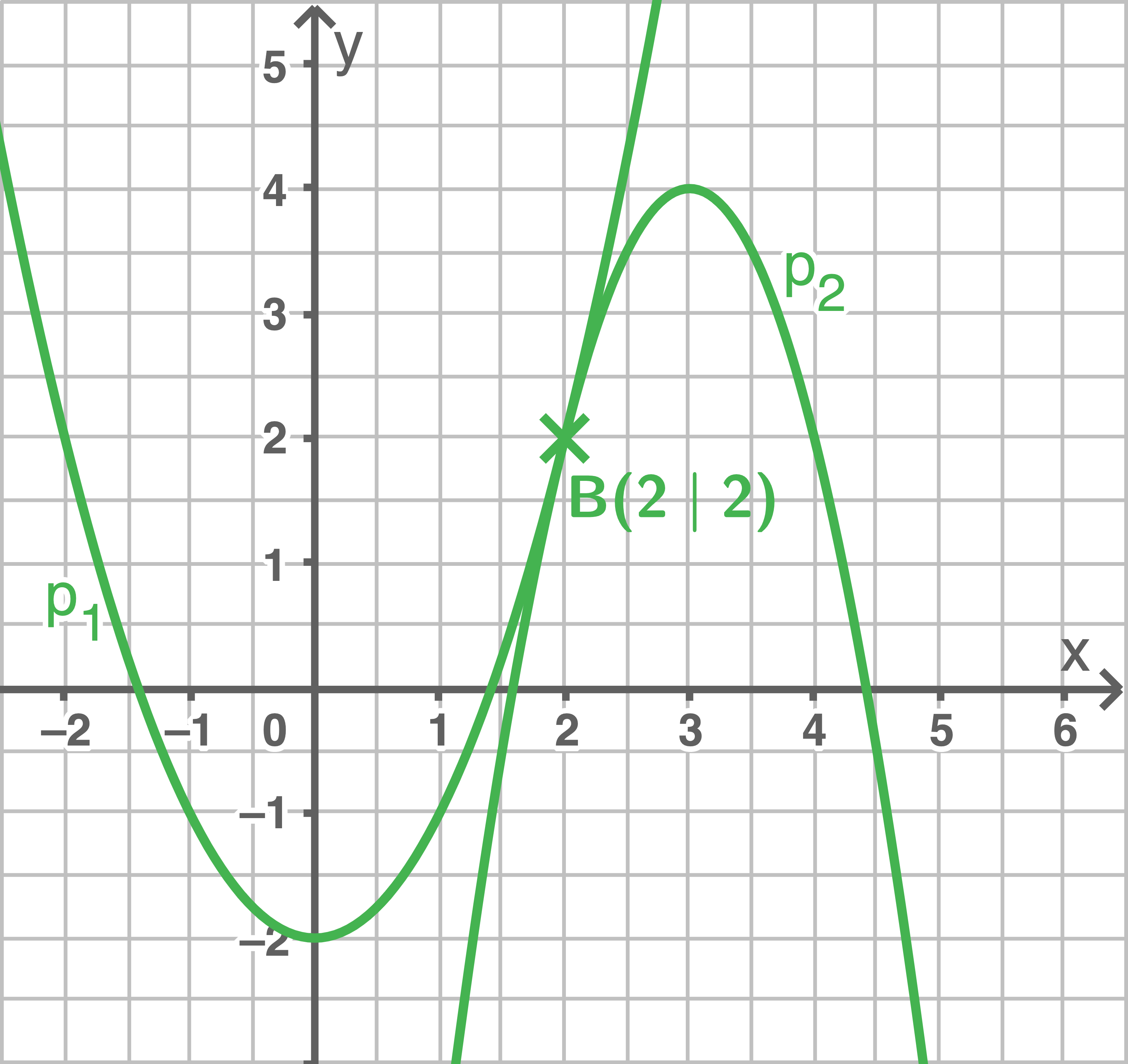
ist die einzige Lösung. Um die 
-Koordinate des Schnittpunkts zu berechnen, wird die 
-Koordinate in eine der beiden Funktionsgleichungen eingesetzt:
in 
Am Schaubild lässt sich erkennen, dass sich die Parabeln in diesem Punkt nur berühren und nicht schneiden. Der Schnittpunkt wird daher auch Berührpunkt genannt.
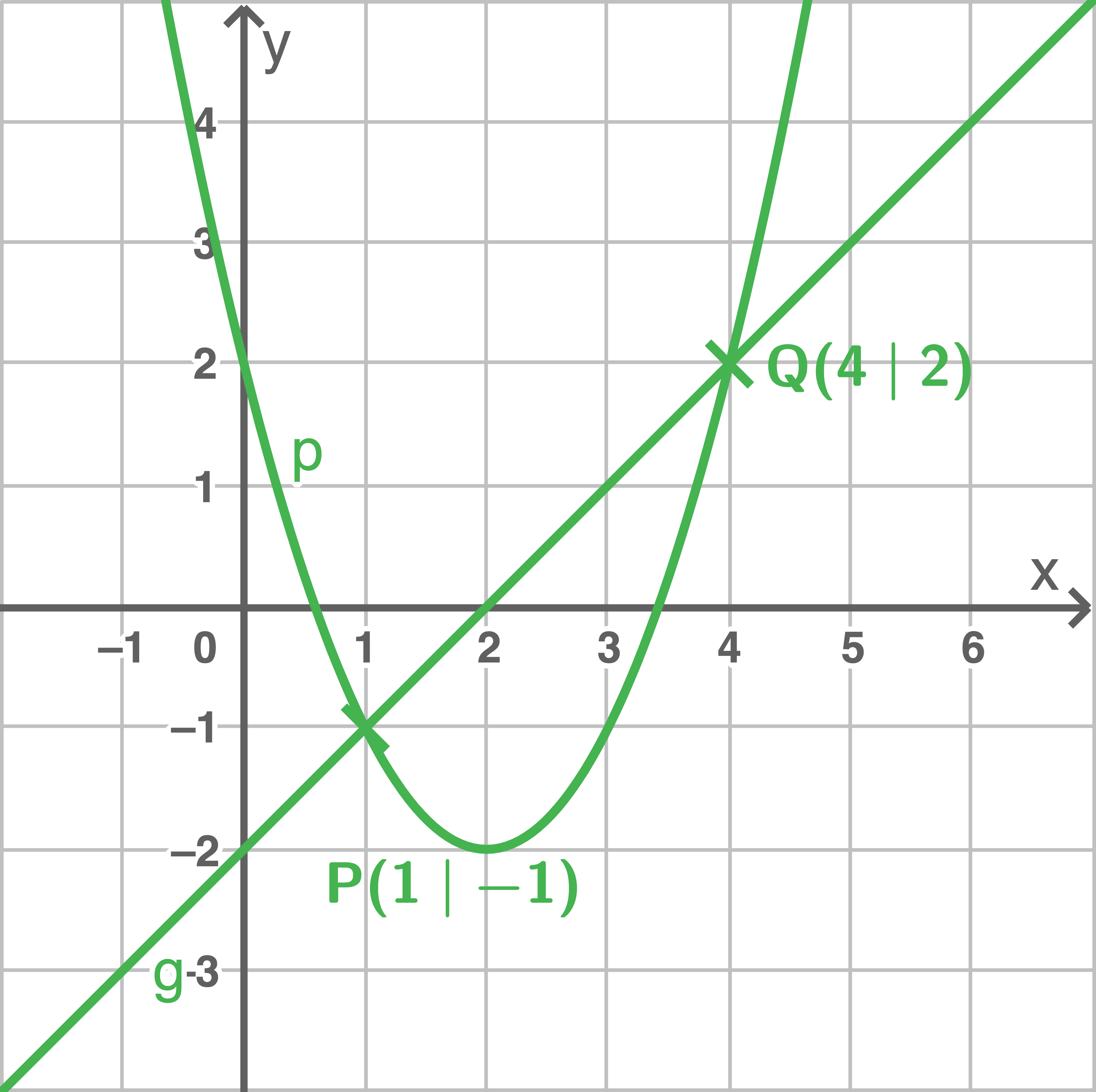
-Koordinaten der Schnittpunkte zu berechnen, werden die -Koordinaten jeweils in eine der beiden Funktionsgleichungen eingesetzt. Am besten eignet sich dafür die Gerade 
in 
in 
Haben eine Gerade und eine Parabel nur einen gemeinsamen Schnittpunkt, heißt dieser auch Berührpunkt.
Beispiele
Schnittpunkt zweier Parabeln
Schnittpunkt(e) berechnen durch Gleichsetzen:
![\(\begin{array}[t]{rll}
p_1&=&p_2 \\[5pt]
x^2-2&=&-2x^2+12x-14 & \scriptsize \mid\; +2x^2\\[5pt]
3x^2-2&=&12x-14 & \scriptsize \mid\; -12x\\[5pt]
3x^2-12x-2&=&-14 & \scriptsize \mid\; +14\\[5pt]
3x^2-12x+12&=&0& \scriptsize \mid\; :3 \\[5pt]
x^2-4x+4&=&0&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e4c5a55c35b2951b74cc737924c86f7c49a4bc3652a699ac7c2e3ab46a9e880d_light.svg)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=&-\dfrac{-4}{2} \pm \sqrt{\left(\dfrac{-4}{2}\right)^2-4} \\[5pt]
&=&2\pm0\\[5pt]
x&=&2
\end{array}\)](https://www.schullv.de/resources/formulas/87b3a3bbdd5a3e9e9451663762f2f6223121439c0eafbdc4e13299f50010ebbe_light.svg)
ist die einzige Lösung. Um die -Koordinate des Schnittpunkts zu berechnen, wird die -Koordinate in eine der beiden Funktionsgleichungen eingesetzt:
in
Am Schaubild lässt sich erkennen, dass sich die Parabeln in diesem Punkt nur berühren und nicht schneiden. Der Schnittpunkt wird daher auch Berührpunkt genannt.
Schnittpunkt einer Parabel und einer Geraden
Schnittpunkte berechnen durch Gleichsetzen:
![\(\begin{array}[t]{rll}
p&=&g \\[5pt]
x^2-4x+2&=&x-2 & \scriptsize \mid\; -x\\[5pt]
x^2-5x+2&=&-2 & \scriptsize \mid\; +2\\[5pt]
x^2-5x+4&=&0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6f4d85cf2b762ca87114d63eb813309418b016663cac015ce1847398fb863c6e_light.svg)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=&-\dfrac{-5}{2} \pm \sqrt{\left(\dfrac{-5}{2}\right)^2-4} \\[5pt]
&=&2,5\pm 1,5\\[5pt]
x_1&=&1\\[5pt]
x_2&=&4
\end{array}\)](https://www.schullv.de/resources/formulas/9badb49b6a13038e0d68bcce7b6b3ec039f1b298b065d6b4ae0e57d9de1663e7_light.svg)
Um die
-Koordinaten der Schnittpunkte zu berechnen, werden die -Koordinaten jeweils in eine der beiden Funktionsgleichungen eingesetzt. Am besten eignet sich dafür die Gerade
in
in
1
Gib die Schnittpunkte der beiden Graphen an.
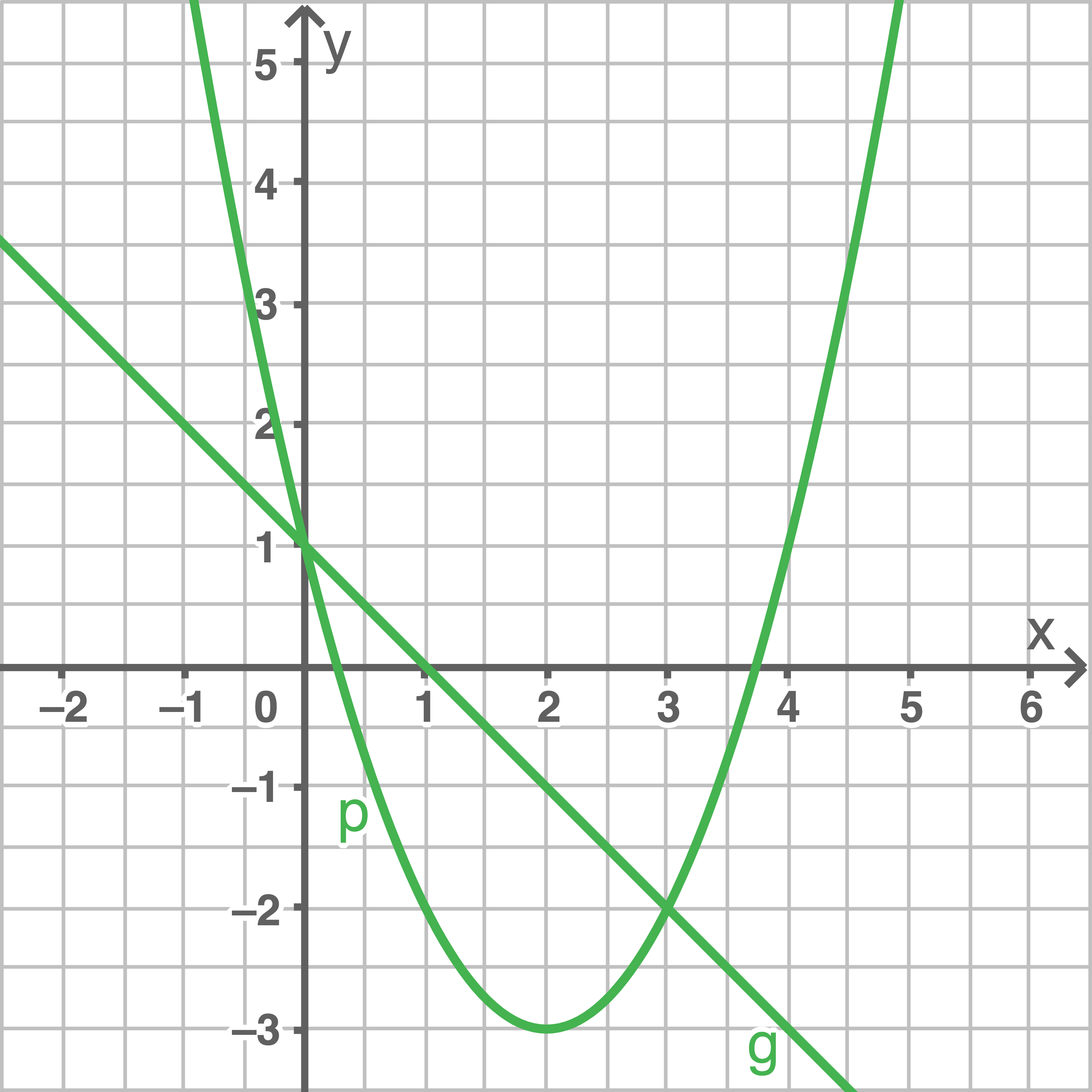
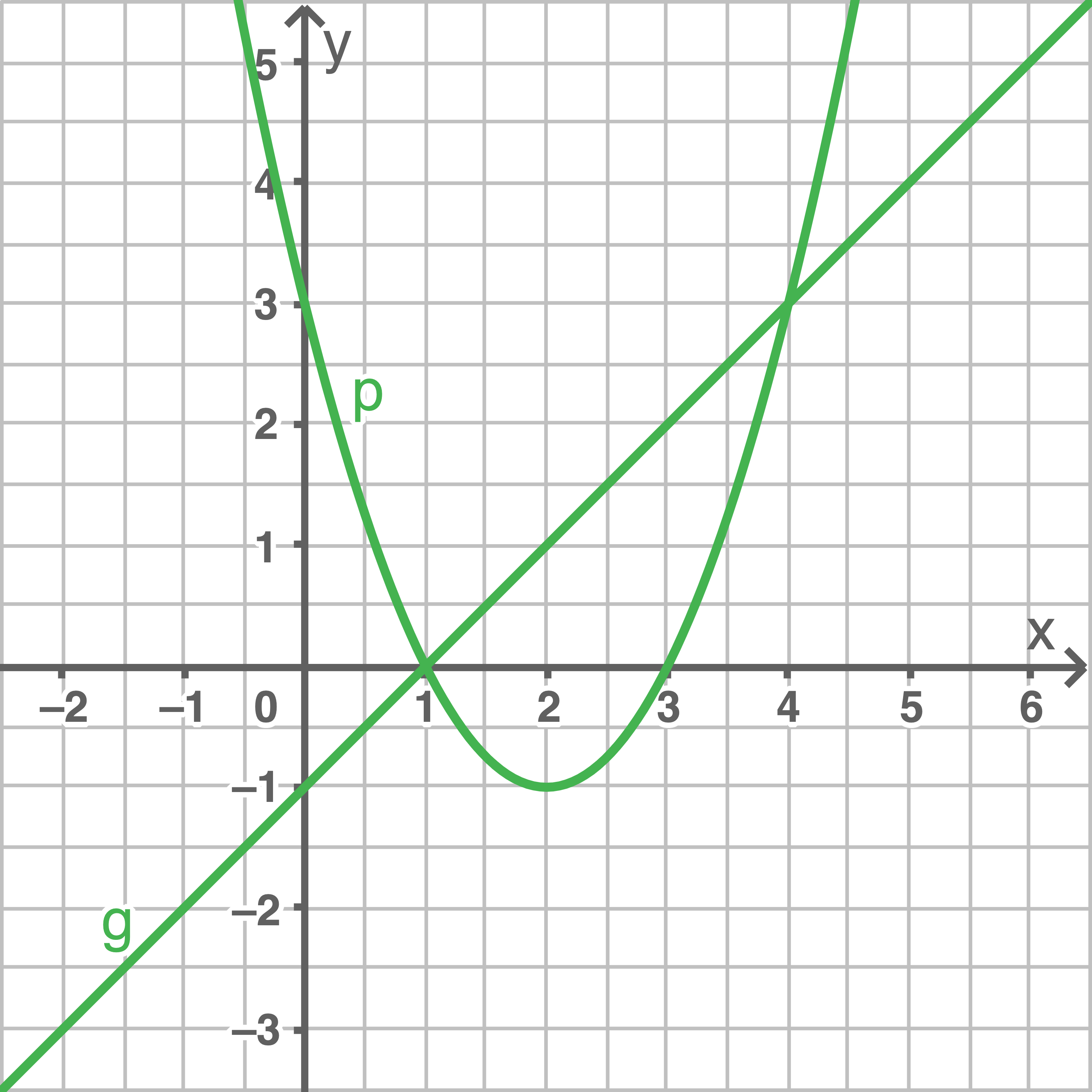
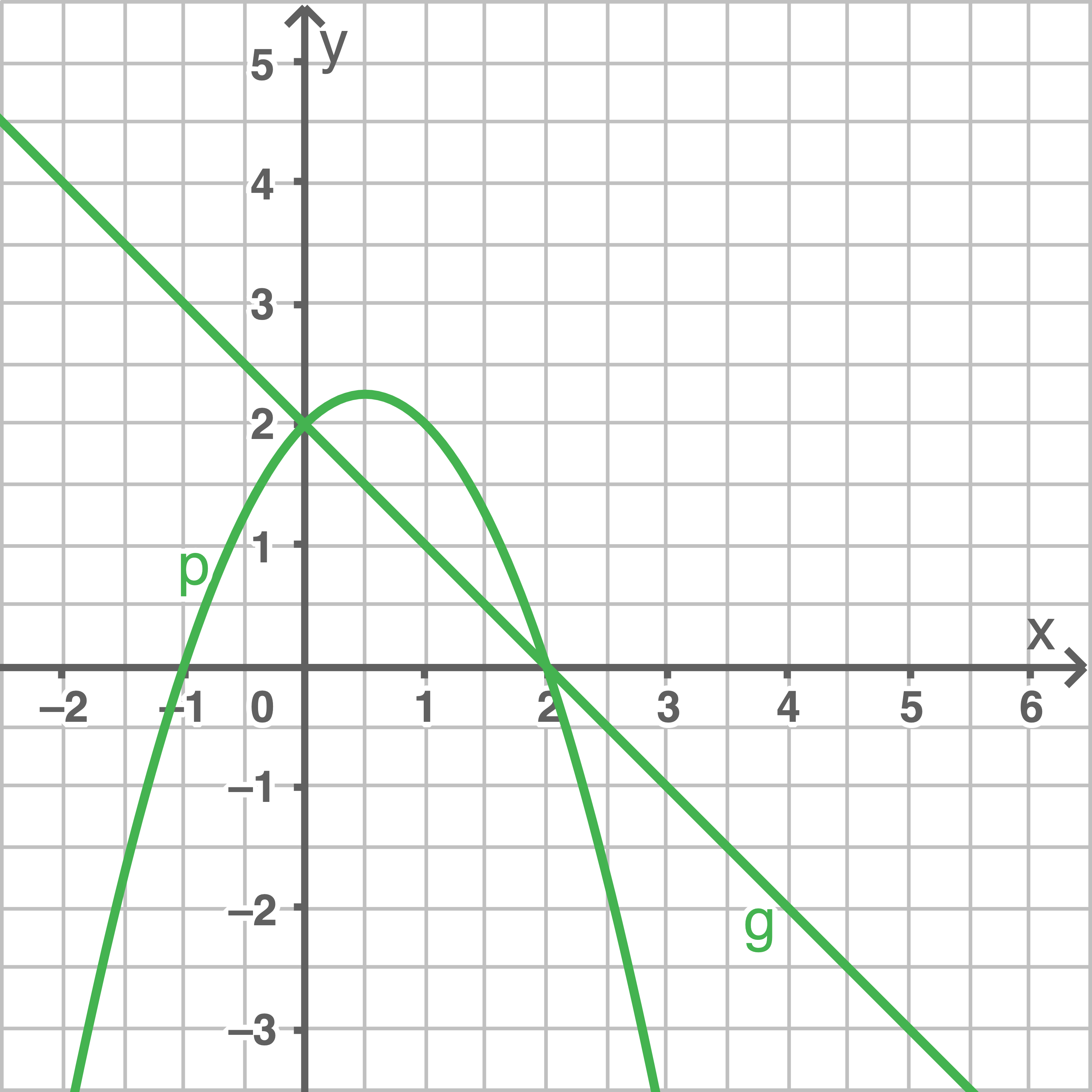
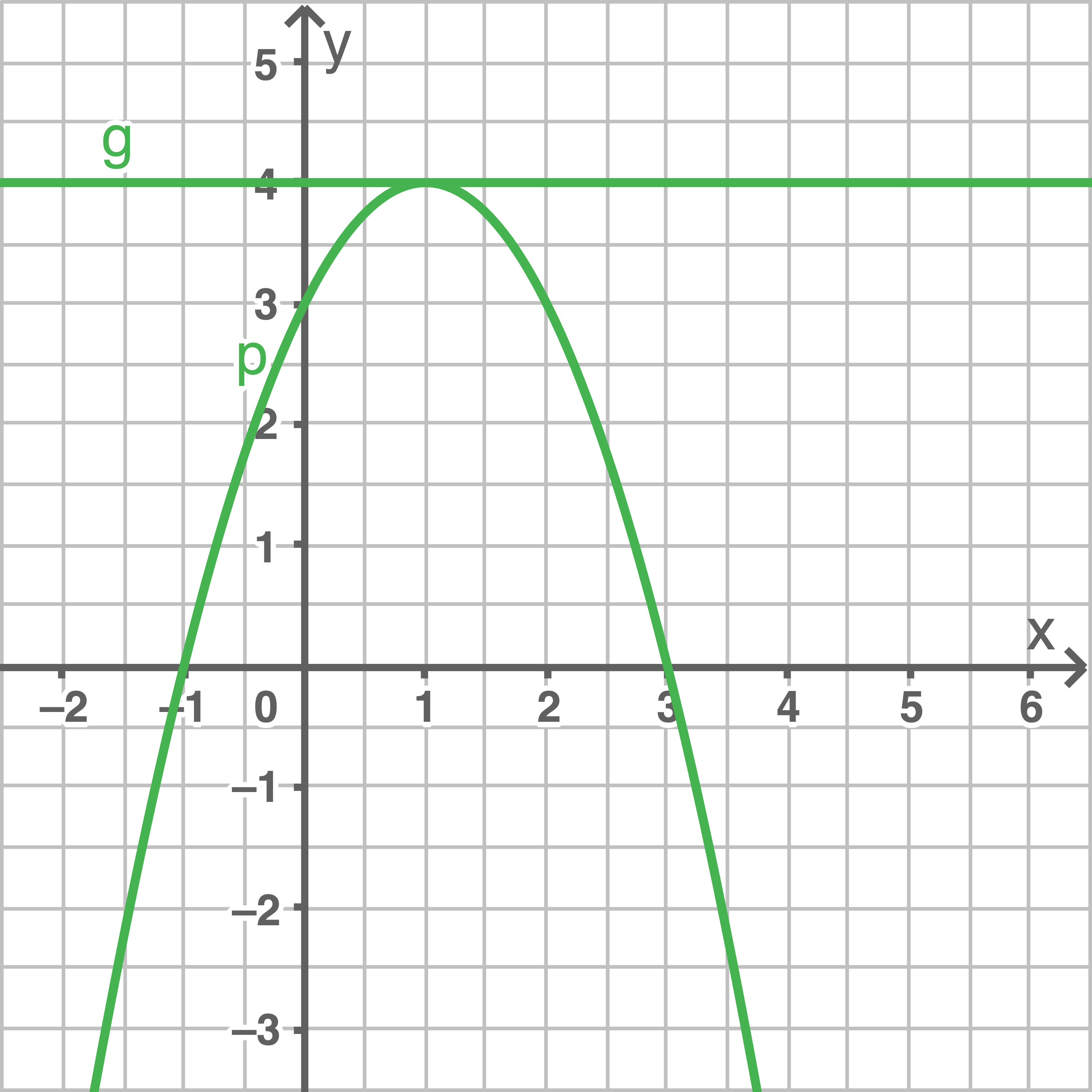
a)
b)
c)
d)
2
Berechne die Schnittpunkte der beiden Parabeln.
a)
b)
c)
d)
e)
f)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
d)
(da nur ein Schnittpunkt)
2
a)
Gleichsetzen
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen: 
in die erste Funktionsgleichung einsetzen: 
![\(\begin{array}[t]{rll}
x^2+2x+1&=&-x^2+2x+3 & \scriptsize \mid\;+x^2 \\[5pt]
2x^2+2x+1&=&2x+3 & \scriptsize \mid\;-2x \\[5pt]
2x^2+1&=&3 & \scriptsize \mid\;-1 \\[5pt]
2x^2&=&2 & \scriptsize \mid\;:2 \\[5pt]
x^2&=&1 & \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
x_1&=&1\\[5pt]
x_2&=&-1
\end{array}\)](https://www.schullv.de/resources/formulas/376ec20058cedb6983a371780f1aefc76c4c3b8b9b996a62ffc9bcdb04ebb222_light.svg)
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen:
in die erste Funktionsgleichung einsetzen:
b)
Gleichsetzen
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen: 
in die erste Funktionsgleichung einsetzen: 
![\(\begin{array}[t]{rll}
x^2+6x-4&=&-x^2-2x+6 & \scriptsize \mid\;+x^2 \\[5pt]
2x^2+6x-4&=&-2x+6 & \scriptsize \mid\;+2x \\[5pt]
2x^2+8x-4&=&6 & \scriptsize \mid\;-6 \\[5pt]
2x^2+8x-10&=&0 & \scriptsize \mid\;:2 \\[5pt]
x^2+4x-5&=&0 & \scriptsize \mid\;:2 \\[5pt]
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{4}{2} \pm \sqrt{\left(\dfrac{4}{2}\right)^2-(-5)} \\[5pt]
&=& -2 \pm 3 \\[5pt]
x_1&=&-5\\[5pt]
x_2&=&1
\end{array}\)](https://www.schullv.de/resources/formulas/fdb09aca142c88c44cd1d78dbcf4ebca4d8b1ac280099710c355fac41adccd48_light.svg)
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen:
in die erste Funktionsgleichung einsetzen:
c)
Gleichsetzen
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen: 
in die erste Funktionsgleichung einsetzen: 
![\(\begin{array}[t]{rll}
2x^2-x-8&=&-x^2-4x-2 & \scriptsize \mid\;+x^2 \\[5pt]
3x^2-x-8&=&-4x-2 & \scriptsize \mid\;+4x \\[5pt]
3x^2+3x-8&=&-2 & \scriptsize \mid\;+2 \\[5pt]
3x^2+3x-6&=&0 & \scriptsize \mid\;:3 \\[5pt]
x^2+x-2&=&0 \\[5pt]
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{1}{2} \pm \sqrt{\left(\dfrac{1}{2}\right)^2-(-2)} \\[5pt]
&=& -\dfrac{1}{2} \pm \dfrac{3}{2} \\[5pt]
x_1&=&1\\[5pt]
x_2&=&-2
\end{array}\)](https://www.schullv.de/resources/formulas/eeb615ee33dbe118701c6ea95e0f02547a41fe7bea0b118f4fe2c208c7b4401b_light.svg)
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen:
in die erste Funktionsgleichung einsetzen:
d)
Gleichsetzen
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen: 
in die erste Funktionsgleichung einsetzen: 
![\(\begin{array}[t]{rll}
x^2-4x+6&=&-x^2+2x+6 & \scriptsize \mid\;+x^2 \\[5pt]
2x^2-4x+6&=&2x+6 & \scriptsize \mid\;-2x \\[5pt]
2x^2-6x+6&=&6 & \scriptsize \mid\;-6 \\[5pt]
2x^2-6x&=&0 \\[5pt]
2x(x-3)&=&0 \\[5pt]
x_1&=&0\\[5pt]
x_2&=&3
\end{array}\)](https://www.schullv.de/resources/formulas/2e4e3dc0736884765b808e1314bdb6e8d1d412b36c7dc49dbf7c8f9a4be1ef00_light.svg)
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen:
in die erste Funktionsgleichung einsetzen:
e)
![\(\begin{array}[t]{rll}
-(x+4)^2-2&=&-x^2-4x+2\\[5pt]
-(x^2+8x+16)-2&=&-x^2-4x+2\\[5pt]
-x^2-8x-16-2&=&-x^2-4x+2\\[5pt]
-x^2-8x-18&=&-x^2-4x+2& \scriptsize \mid\;+x^2 \\[5pt]
-8x-18&=&-4x+2 & \scriptsize \mid\;+8x \\[5pt]
-18&=&4x+2 & \scriptsize \mid\;-2 \\[5pt]
-20&=&4x& \scriptsize \mid\;:4 \\[5pt]
-5&=&x\\[5pt]
x&=&-5
\end{array}\)](https://www.schullv.de/resources/formulas/24da3c369874555869aa560d0c00586ef1c6c081393aa6450c8a32ffce8a0633_light.svg)
in die erste Funktionsgleichung einsetzen: 
f)
Gleichsetzen
![\(\begin{array}[t]{rll}
(x-2)^2+3&=& -(x-3)^2+4\\[5pt]
x^2-4x+4+3&=& -(x^2-6x+9)+4\\[5pt]
x^2-4x+7&=& -x^2+6x-9+4\\[5pt]
x^2-4x+7&=& -x^2+6x-5& \scriptsize \mid\;+x^2\\[5pt]
2x^2-4x+7&=& 6x-5& \scriptsize \mid\;-6x\\[5pt]
2x^2-10x+7&=& -5& \scriptsize \mid\;+5\\[5pt]
2x^2-10x+12&=& 0 & \scriptsize \mid\;:2 \\[5pt]
x^2-5x+6&=& 0 \\[5pt]
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-5}{2} \pm \sqrt{\left(\dfrac{-5}{2}\right)^2-6} \\[5pt]
&=& \dfrac{5}{2} \pm \dfrac{1}{2} \\[5pt]
x_1&=& 3\\[5pt]
x_2&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/4332eb6101c0e971c3e0acc07cac9d6999f31fe0f3670875f79736ffef88aebd_light.svg)
-Koordinaten berechnen
in die erste Funktionsgleichung einsetzen: 
in die erste Funktionsgleichung einsetzen: 
