Katheten
Sind die Längen der Hypotenuse und einer Kathete gegeben, lässt sich mit dem Satz des Pythagoras die Länge der anderen Kathete berechnen.
Beispiel
 berechnen. Dafür wird die Formel umgestellt:
berechnen. Dafür wird die Formel umgestellt:
![\(\begin{array}[t]{rll}
a^2+b^2&=&c^2 &\quad \scriptsize \mid\; -a^2\\[5pt]
b^2&=&c^2-a^2 &\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
b&=&\sqrt{c^2-a^2} &\\[5pt]
b&=&\sqrt{(10\,\text{cm})^2-(6\,\text{cm})^2} &\\[5pt]
b&=&\sqrt{100\,\text{cm}^2-36\,\text{cm}^2} &\\[5pt]
b&=&\sqrt{64\,\text{cm}^2} &\\[5pt]
b&=&8\,\text{cm} &\\[5pt]
\end{array}\)](https://mathjax.schullv.de/42fe4ff79499c33a0835ae3d998fb2c01e8c5705dff71b5ad50827a180a395a3?color=5a5a5a)
Für das nebenstehende rechtwinklige Dreieck gilt:
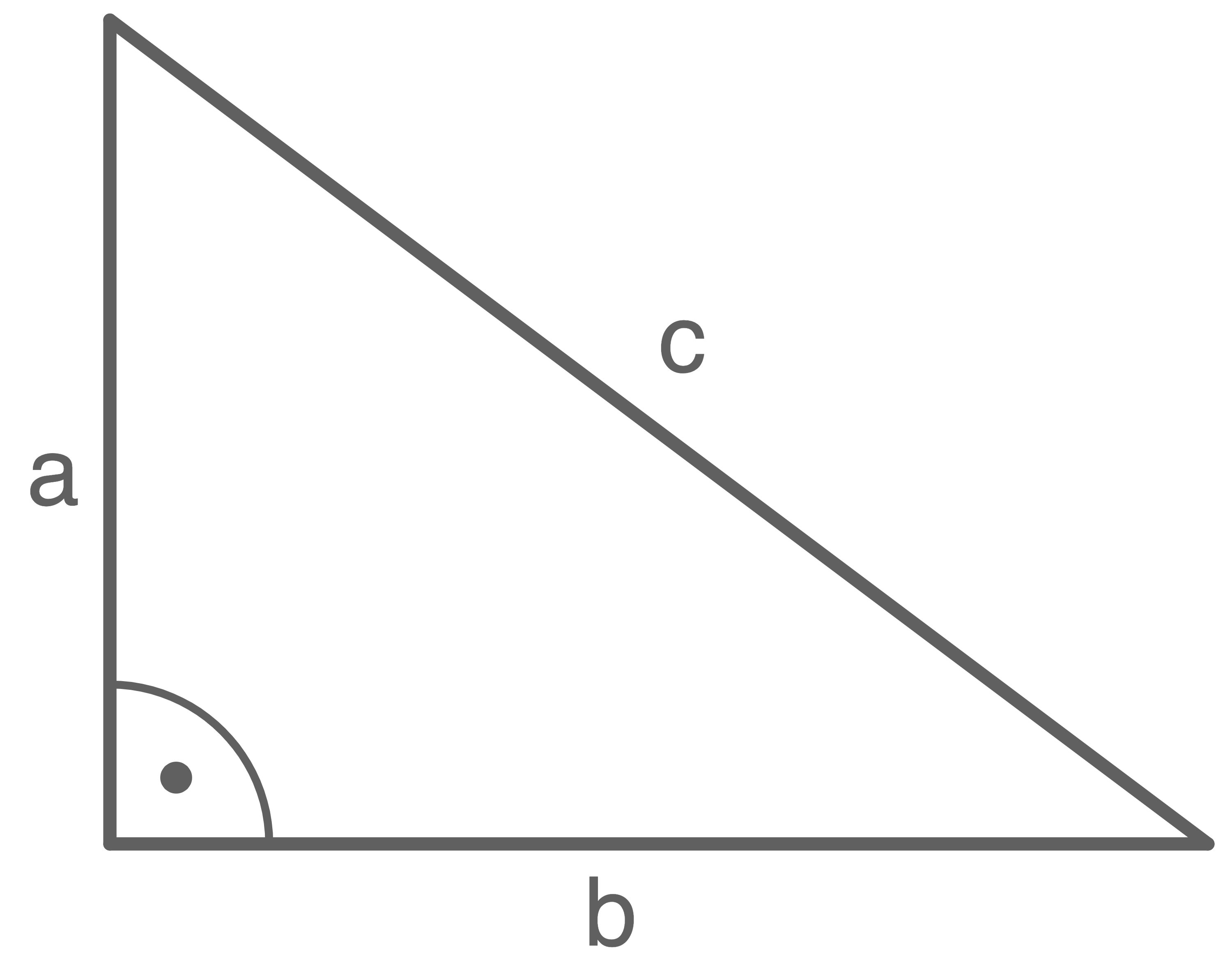 Die Seiten
Die Seiten  und
und  umschließen den rechten Winkel und sind somit die Katheten.
umschließen den rechten Winkel und sind somit die Katheten.
Die Seite liegt gegenüber vom rechten Winkel und bildet also die Hypotenuse.
liegt gegenüber vom rechten Winkel und bildet also die Hypotenuse.
Mit dem Satz des Pythagoras lässt sich nun die Länge der Kathete 
Die Seite
1
2
Es sind jeweils die Hypotenuse und eine Kathete gegeben.
Berechne mit dem Satz des Pythagoras die andere Kathete.
a)
- Kathete:
- Hypothenuse:
b)
- Kathete:
- Hypothenuse:
c)
- Kathete:
- Hypothenuse:
d)
- Kathete:
- Hypothenuse:
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
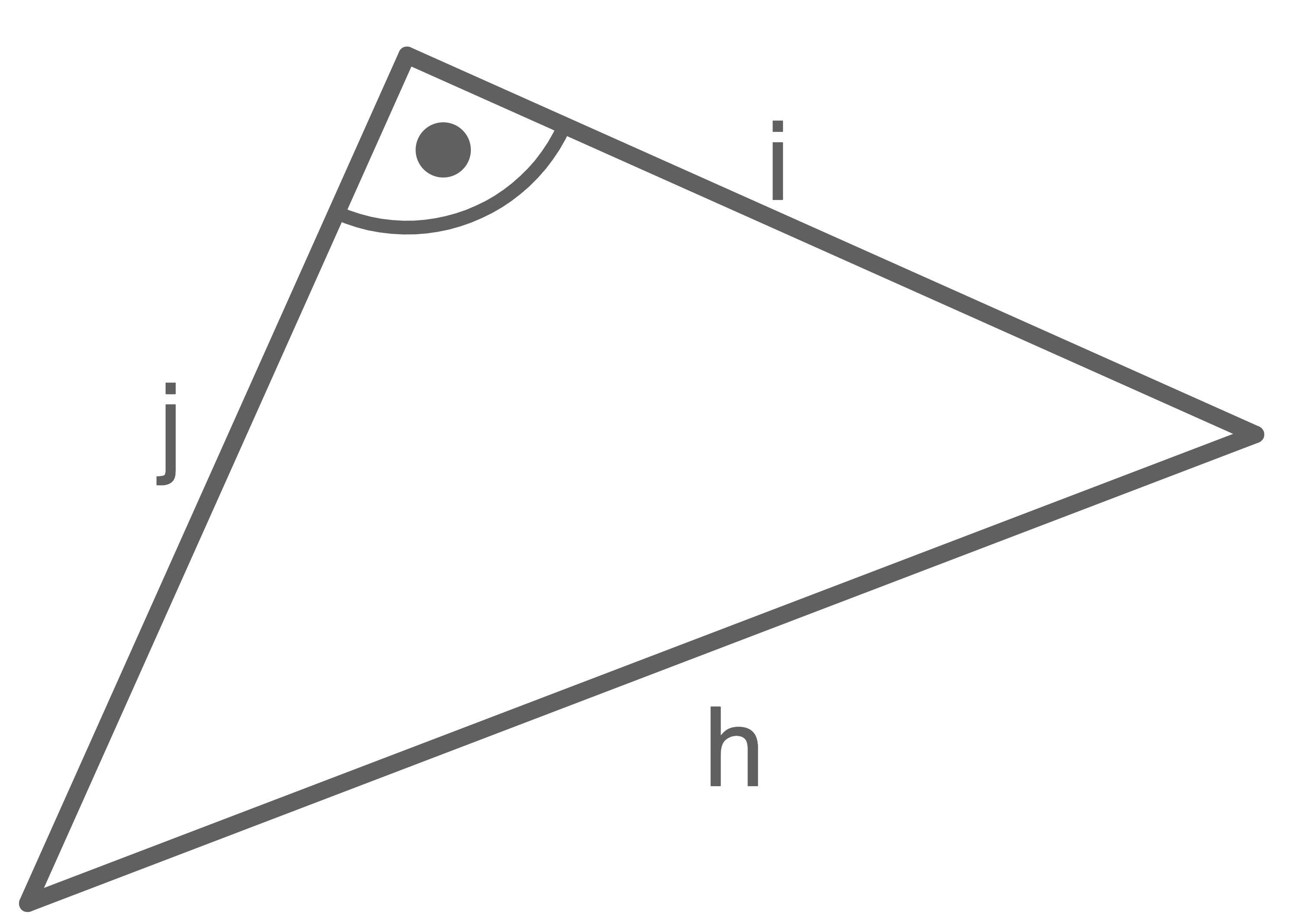
Die Seite  ist die zweite Kathete.
ist die zweite Kathete.
![\(\begin{array}[t]{rll}
i^2+j^2&=&h^2 &\quad \scriptsize \mid\;-i^2 \\[5pt]
j^2&=&h^2-i^2 \\[5pt]
j^2&=&(18,3\,\text{cm})^2-(14,6\,\text{cm})^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
j&=&\sqrt{(18,3\,\text{cm})^2-(14,6\,\text{cm})^2} \\[5pt]
j&=&\sqrt{121,73\,\text{cm}^2} \\[5pt]
j&=&11,0\,\text{cm} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/cae2fdac4e7550af70828f63438bf01b06b1103356099d78f0bc41dd819d50f1?color=5a5a5a)
2
a)
b)
c)
d)