Ähnlichkeitssätze in Dreiecken
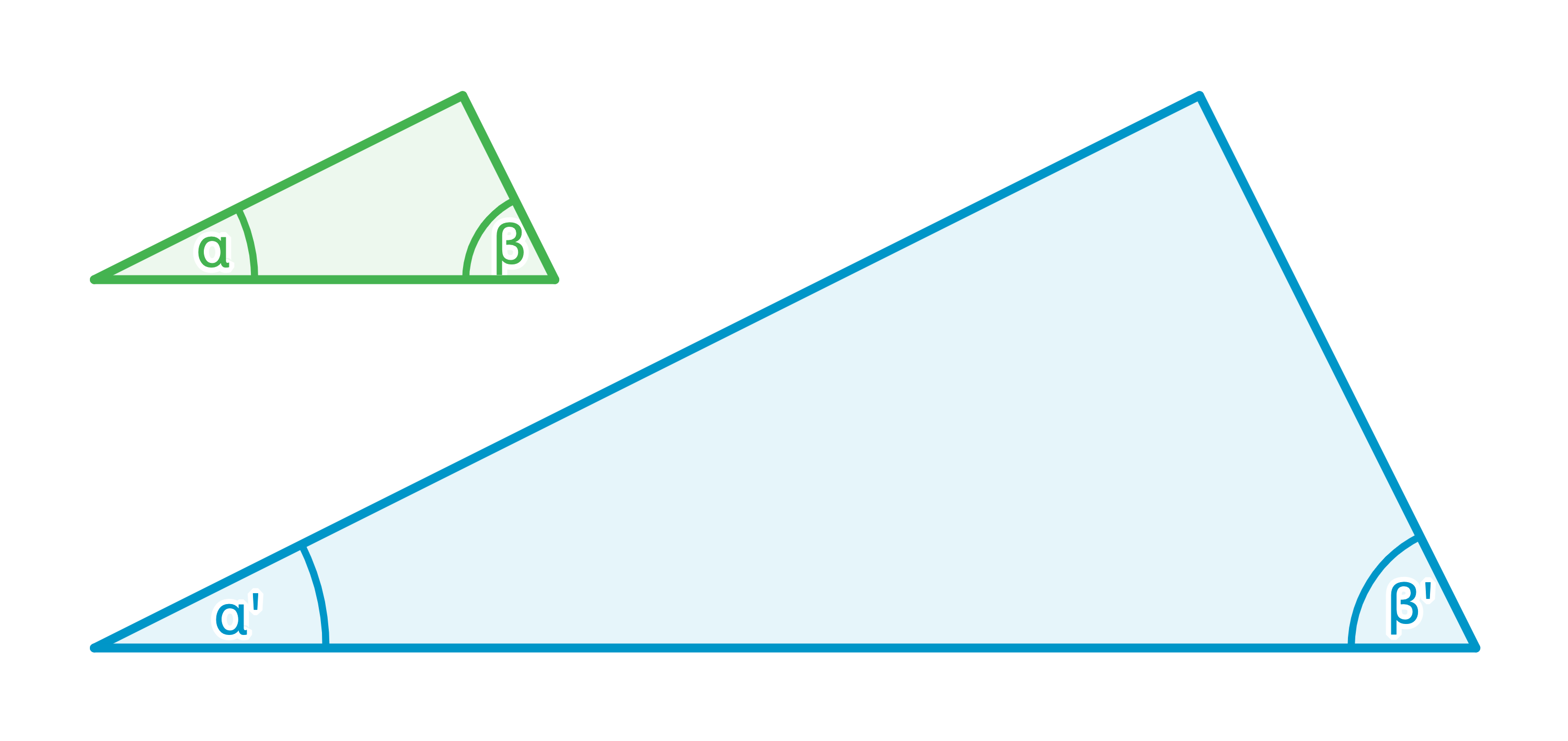
Ähnlichkeitssatz WW
Zwei Dreiecke 
und 
sind zueinander ähnlich, wenn sie in zwei Winkeln (WW) übereinstimmen.
und 
und sind zueinander ähnlich, wenn sie in zwei Winkeln (WW) übereinstimmen.
und
Ähnlichkeitssatz SSS
Zwei Dreiecke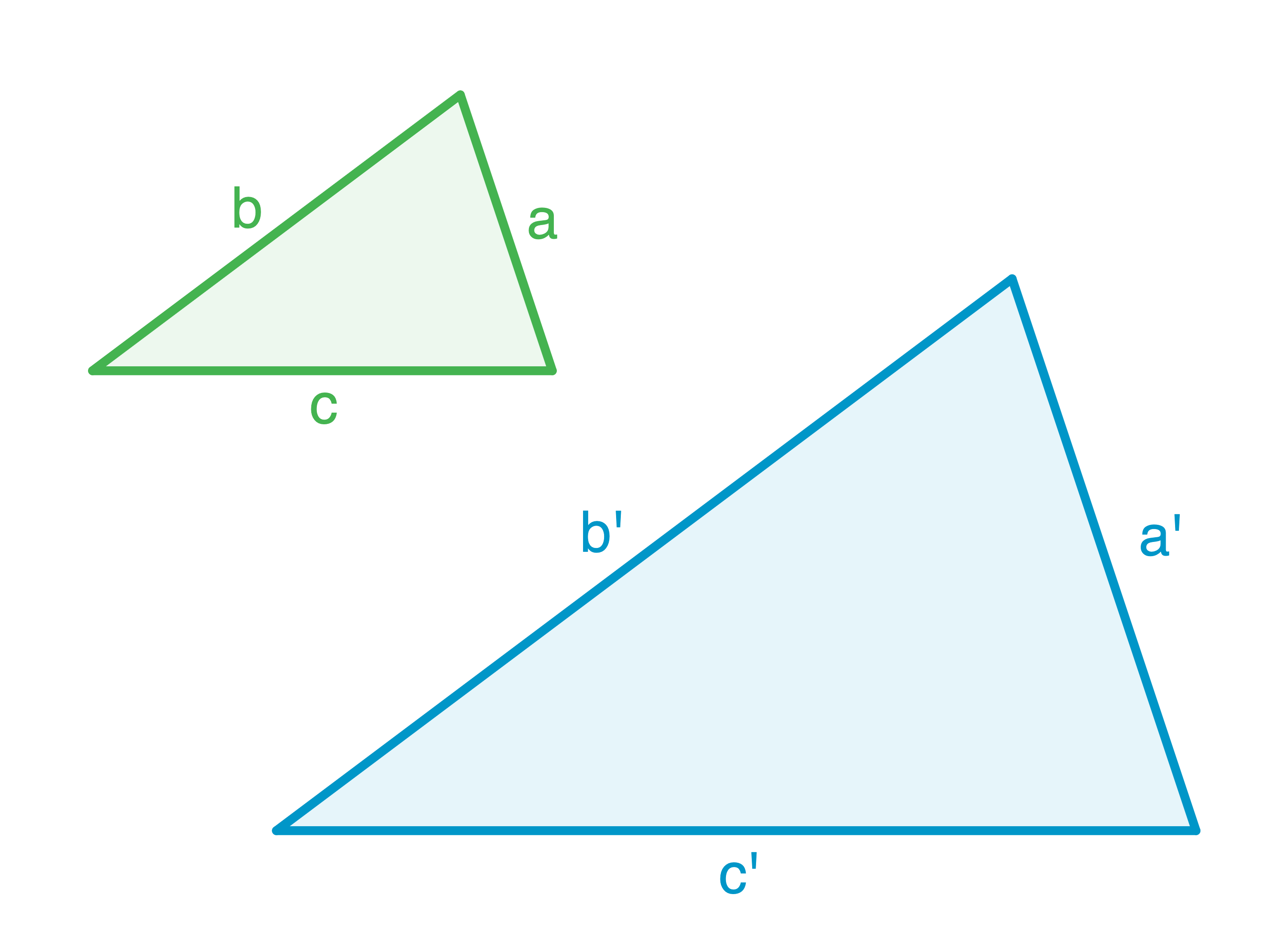 und sind zueinander ähnlich, wenn alle zusammengehörigen Seiten (SSS) das gleiche Längenverhältnis besitzen.
1
Begründe, ob die Dreiecke jeweils ähnlich zueinander sind.
a)
Für das Dreieck 
gilt:
gilt:
gilt:
gilt:
b)
Für das Dreieck 
gilt:
gilt:
gilt:
gilt:
c)
Für das Dreieck 
gilt:
gilt:
gilt:
gilt:
d)
Für das Dreieck 
gilt:
gilt:
gilt:
gilt:
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Mit dem Ähnlichkeitssatz SSS kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Längenverhältnis 1
Längenverhältnis 2
Längenverhältnis 3
Da alle zusammengehörigen Seiten das gleiche Längenverhältnis haben, gilt: Die Dreiecke sind ähnlich.
Längenverhältnis 2
Längenverhältnis 3
Da alle zusammengehörigen Seiten das gleiche Längenverhältnis haben, gilt: Die Dreiecke sind ähnlich.
b)
Mit dem Ähnlichkeitssatz WW kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Größe des Winkels 
![\(\begin{array}[t]{rll}
\gamma&=&180^{\circ}-\alpha-\beta &\\[5pt]
\gamma&=&180^{\circ}-35^{\circ}-90^{\circ} &\\[5pt]
\gamma&=&55^{\circ}&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f8b4f60fa0192bc3b57b54a8ab49bc41e863e7621037001a4eab6e49b9824b41_light.svg)
Es gilt: 
Die Dreiecke sind nicht ähnlich.
Es gilt: Die Dreiecke sind nicht ähnlich.
c)
Mit dem Ähnlichkeitssatz SSS kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Längenverhältnis 1
Längenverhältnis 2
Längenverhältnis 3
Das Längenverhältnis der Seiten 
und 
stimmt nicht mit dem Längenverhältnis der anderen Seiten überein. Somit gilt: Die Dreiecke sind nicht ähnlich.
Längenverhältnis 2
Längenverhältnis 3
Das Längenverhältnis der Seiten und stimmt nicht mit dem Längenverhältnis der anderen Seiten überein. Somit gilt: Die Dreiecke sind nicht ähnlich.
d)
Mit dem Ähnlichkeitssatz WW kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Größe des Winkels 
![\(\begin{array}[t]{rll}
\alpha&=&180^{\circ}-\beta-\gamma &\\[5pt]
\alpha&=&180^{\circ}-83^{\circ}-36^{\circ} &\\[5pt]
\alpha&=&61^{\circ}&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f8c92f5d917824da0bd68e6e3489adca6800e2e1da24ee145605592c8d11017b_light.svg)
Somit gilt: und 
Die Dreiecke sind also ähnlich.
Somit gilt: und Die Dreiecke sind also ähnlich.