Parabeln als Ortslinien
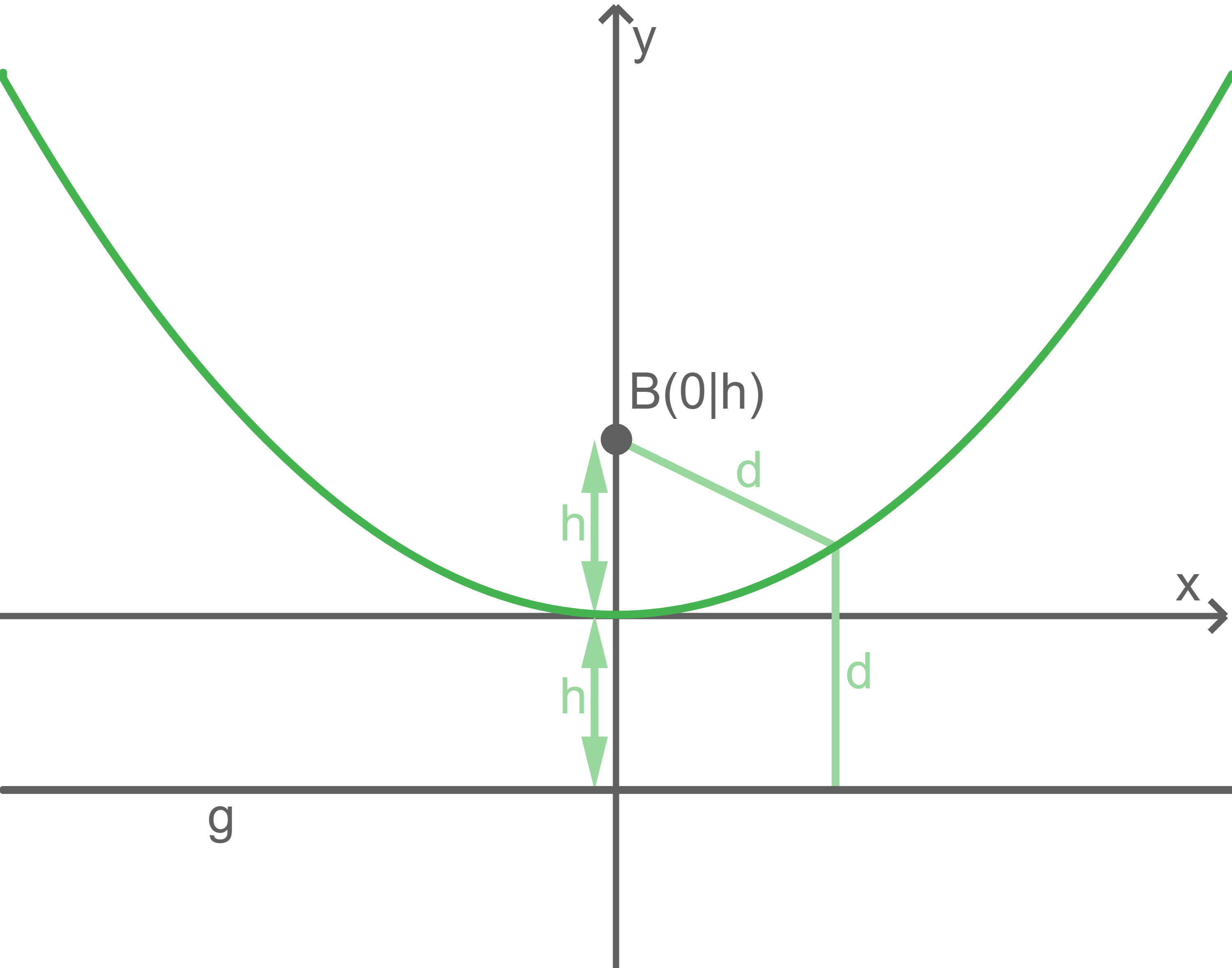
Der Punkt 
wird als Brennpunkt bezeichnet. Eine Gerade 
die sogenannte Leitlinie, verläuft nicht durch 
Dann liegen alle Punkte die den gleichen Abstand zu und 
besitzen auf einer Parabel.
Diese Parabel besitzt für den Brennpunkt 
und die Leitlinie 
mit 
die allgemeine Form 
Andersherum liefert eine gegebene Parabel mit 
den Brennpunkt mit den allgemeinen Koordinaten 
und die zugehörige Leitlinie 
gegeben durch 
1
Gib den zu der jeweiligen Parabel gehörenden Brennpunkt und die Leitlinie an und zeichne die Elemente in ein passendes Koordinatensystem ein.
a)
b)
c)
d)
2
Bei einem Hallenfußballturnier mit einer Deckenhöhe von konstant 
Metern steht ein Spieler mit Ball vor dem 
Meter großen gegnerischen Torhüter. Er möchte den Ball so über den Torhüter schießen, dass dieser zu jedem Zeitpunkt gleichweit von der Decke, sowie vom höchsten Punkt des Torhüters entfernt ist. Das Tor, welches der Spieler anvisiert, steht Meter hinter dem Torhüter und besitzt eine Höhe von 
Metern. Ein Meter entpricht hierbei einer Längeneinheit im Koordinatensystem. Trifft der Spieler mit seinem Schuss das Tor?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
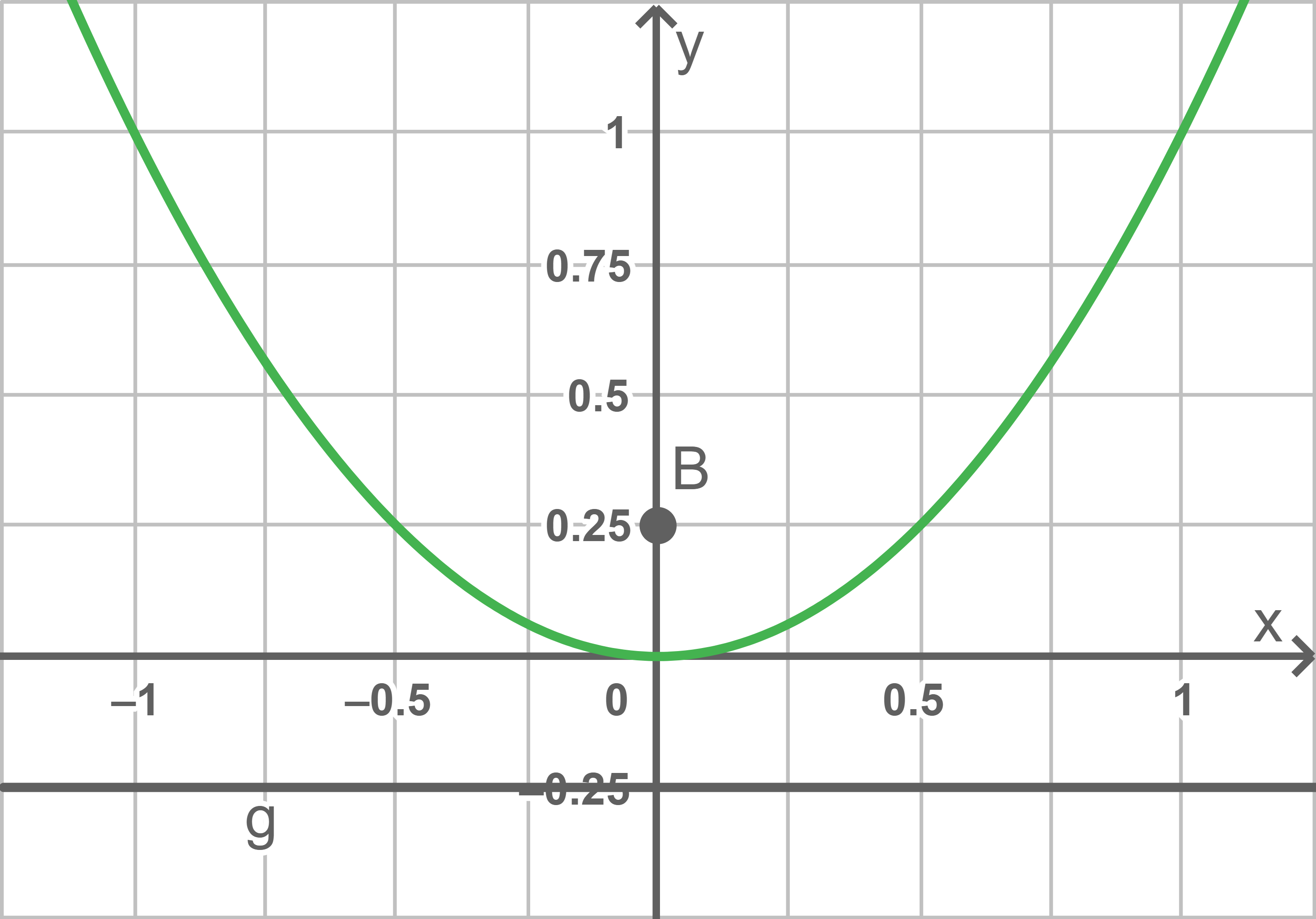
Die betrachtete Parabel ist gegeben durch 
In diesem Fall gilt somit 
Der zugehörige Brennpunkt besitzt damit die Koordinaten 
und die Leitlinie ist gegeben durch 
b)
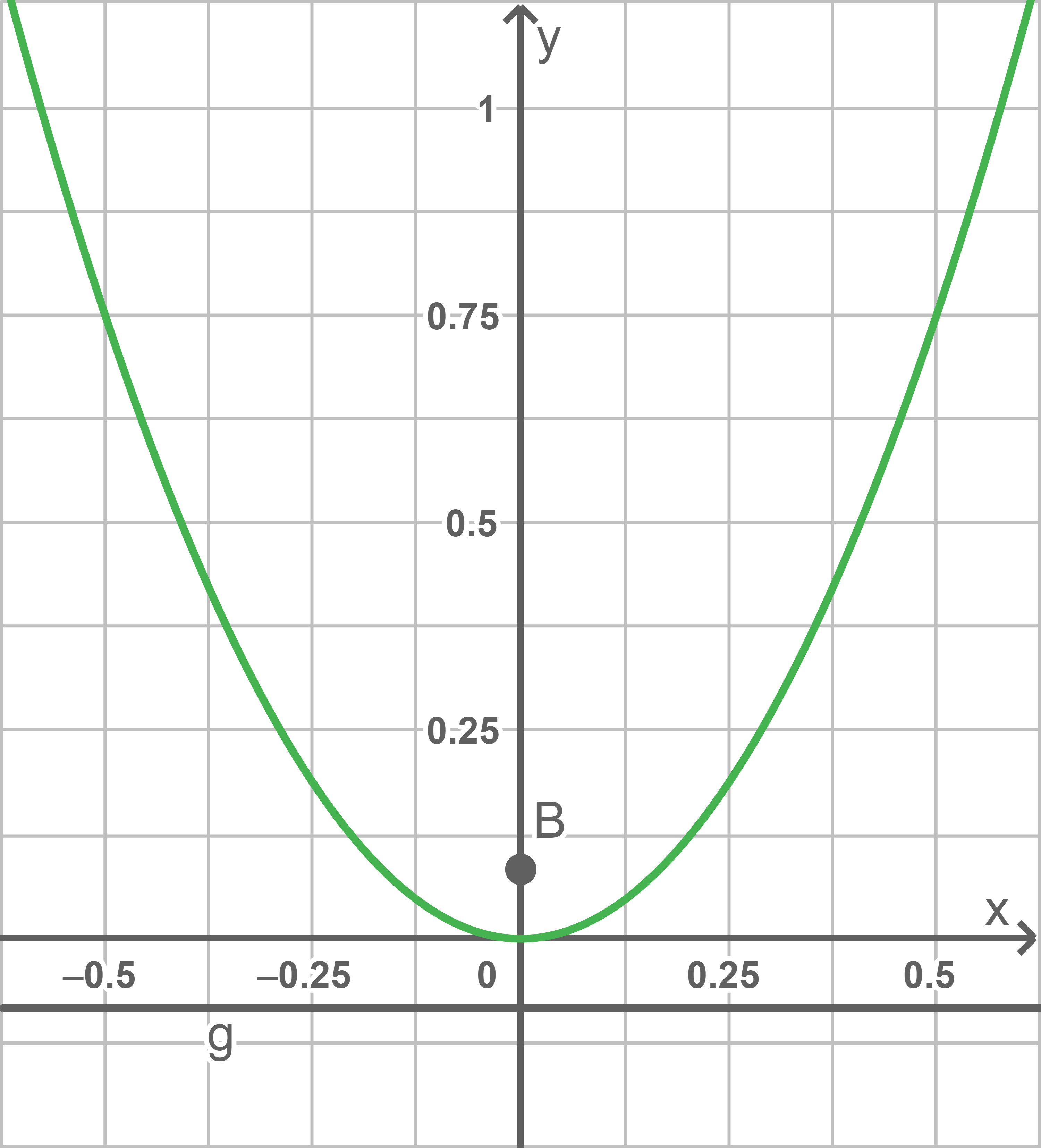
Die Gleichung der Parabel lautet 
Somit gilt hier 
Der zugehörige Brennpunkt besitzt damit die Koordinaten 
und die Leitlinie ist gegeben durch 
c)
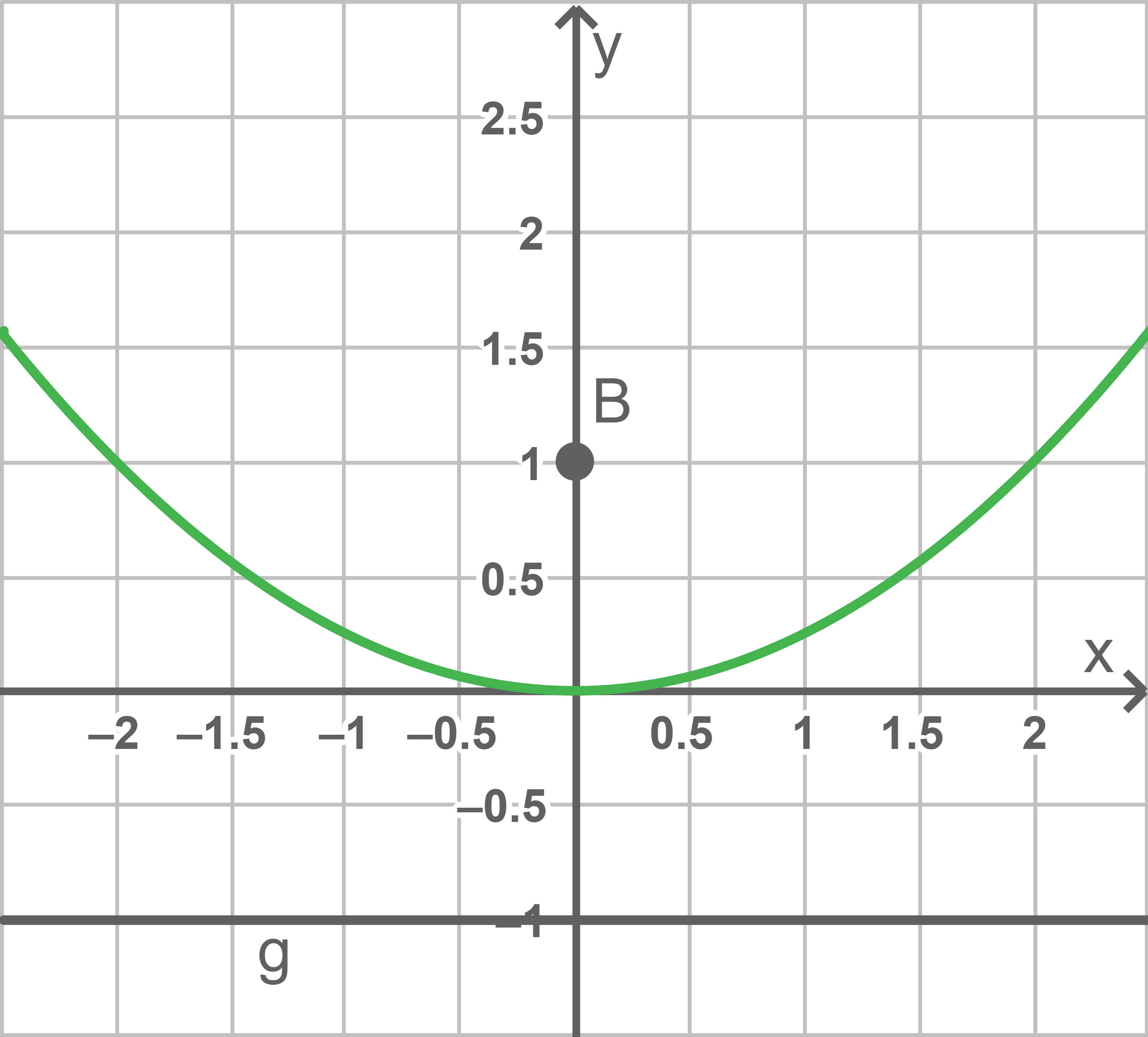
In dieser Aufgabe ist die Gleichung der betrachteten Parabel 
das heißt es gilt 
Der Brennpunkt ergibt sich somit als 
und die Leitlinie besitzt die Gleichung 
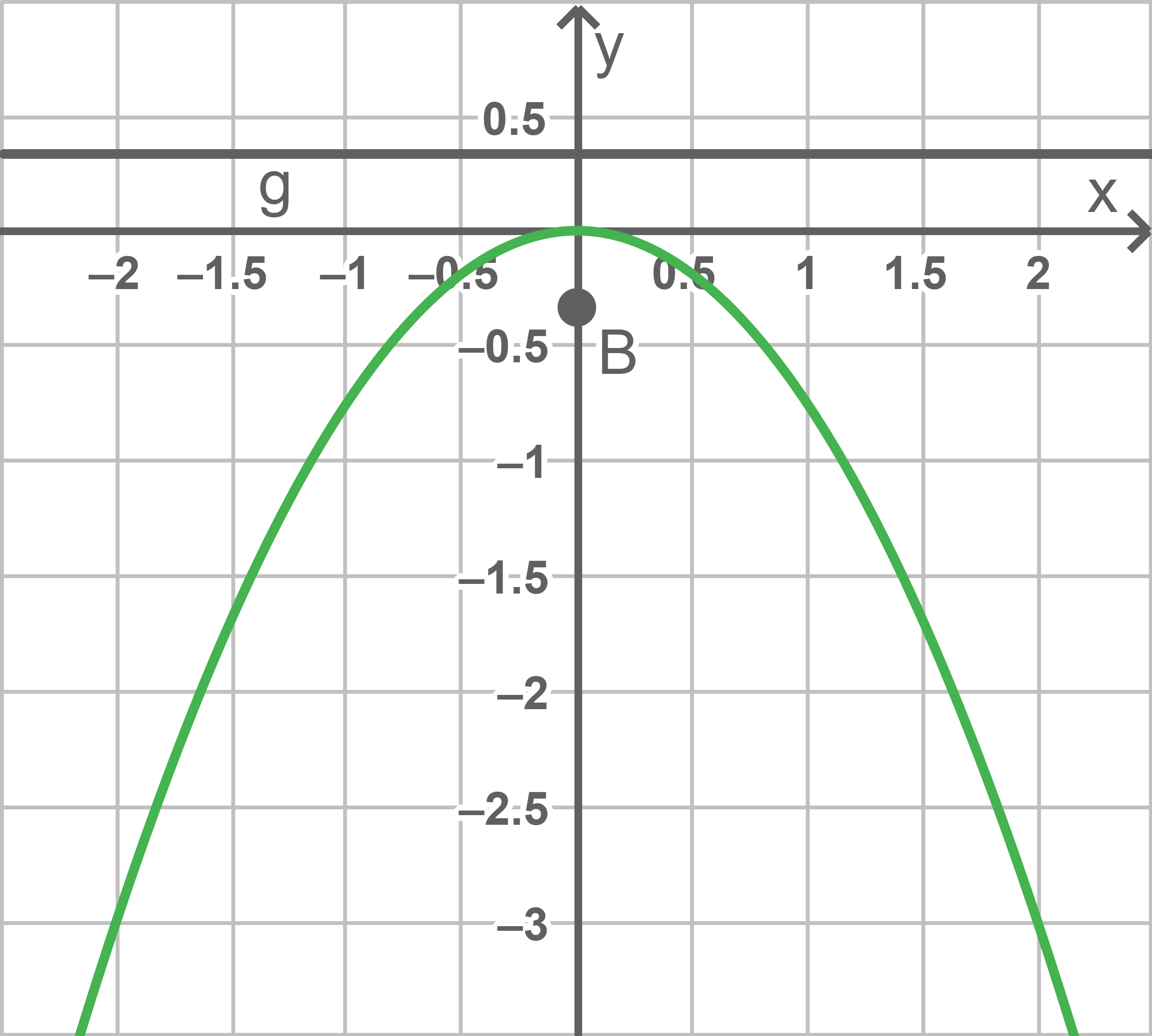
d)
Die betrachtete Parabel ist gegeben durch die Gleichung 
somit gilt Der zugehörige Brennpunkt besitzt damit die Koordinaten 
und die Leitlinie ist gegeben durch 
2
Um die Gleichung der Parabel über die allgemeine Form ausrechnen zu können, muss die 
-Achse mittig zwischen dem Brennpunkt 
das heißt dem höchsten Punkt des Torhüters, und der Leitlinie hier der Hallendecke, verlaufen. Zudem muss der Torhüter an der Stelle 
stehen. Aus den Längenangaben der Aufgabenstellung folgt somit 
und die Gleichung 
für 
Die parabelförmige Flugbahn des Fußballs wird somit durch die folgende Gleichung beschrieben:
Das Tor steht laut Aufgabenstellung zwei Meter hinter dem Torhüter, das heißt im Punkt mit den Koordinaten 
Da das Tor eine Höhe von Metern besitzt, befindet sich der höchste Punkt des Tores in 
Um zu überprüfen, ob der Schuss im Tor landet, wird somit 
in die Gleichung der Flugbahn eingesetzt:
![\(\begin{array}[t]{rll}
y&=&-\dfrac{1}{4} \cdot (-2)^2 \\[5pt]
&=&-\dfrac{1}{4} \cdot 4 \\[5pt]
&=&-1
\end{array}\)](https://mathjax.schullv.de/39f753d28c30f3967c23cb63b141eb0d103791eb032e3ad0cc334a34ea361edc?color=5a5a5a)
Da 
gilt, erzielt der Spieler somit mit seinem Schuss ein Tor.