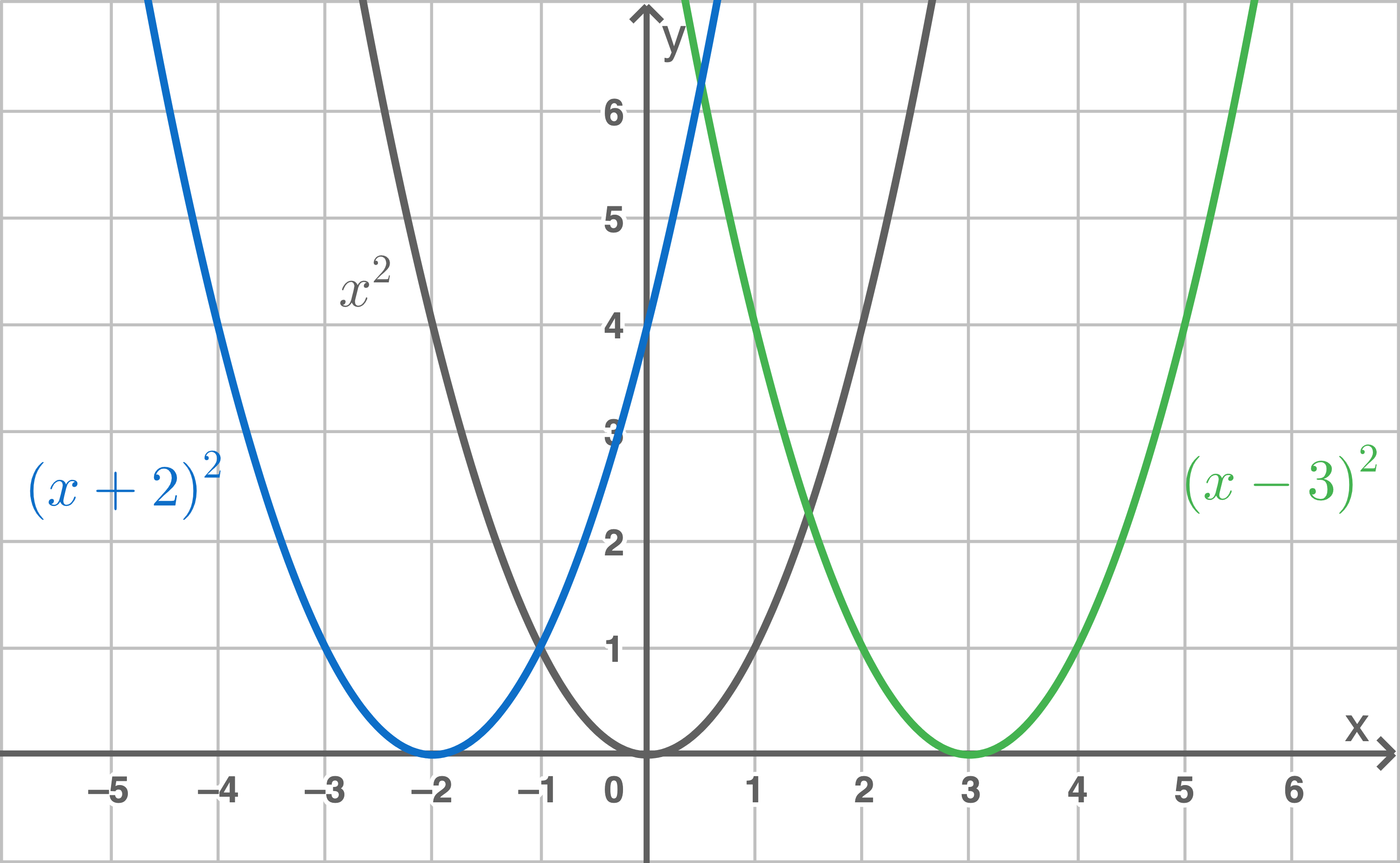
Verschieben der Normalparabel
Verschieben der Normalparabel in x-Richtung
Der Graph einer verschobenen Normalparabel der Form 
ergibt sich, indem der Graph der Normalparabel um 
Einheiten entlang der 
-Achse verschoben wird:
und ist symmetrisch zur Geraden 
Verschiebung nach links
Verschiebung nach rechts
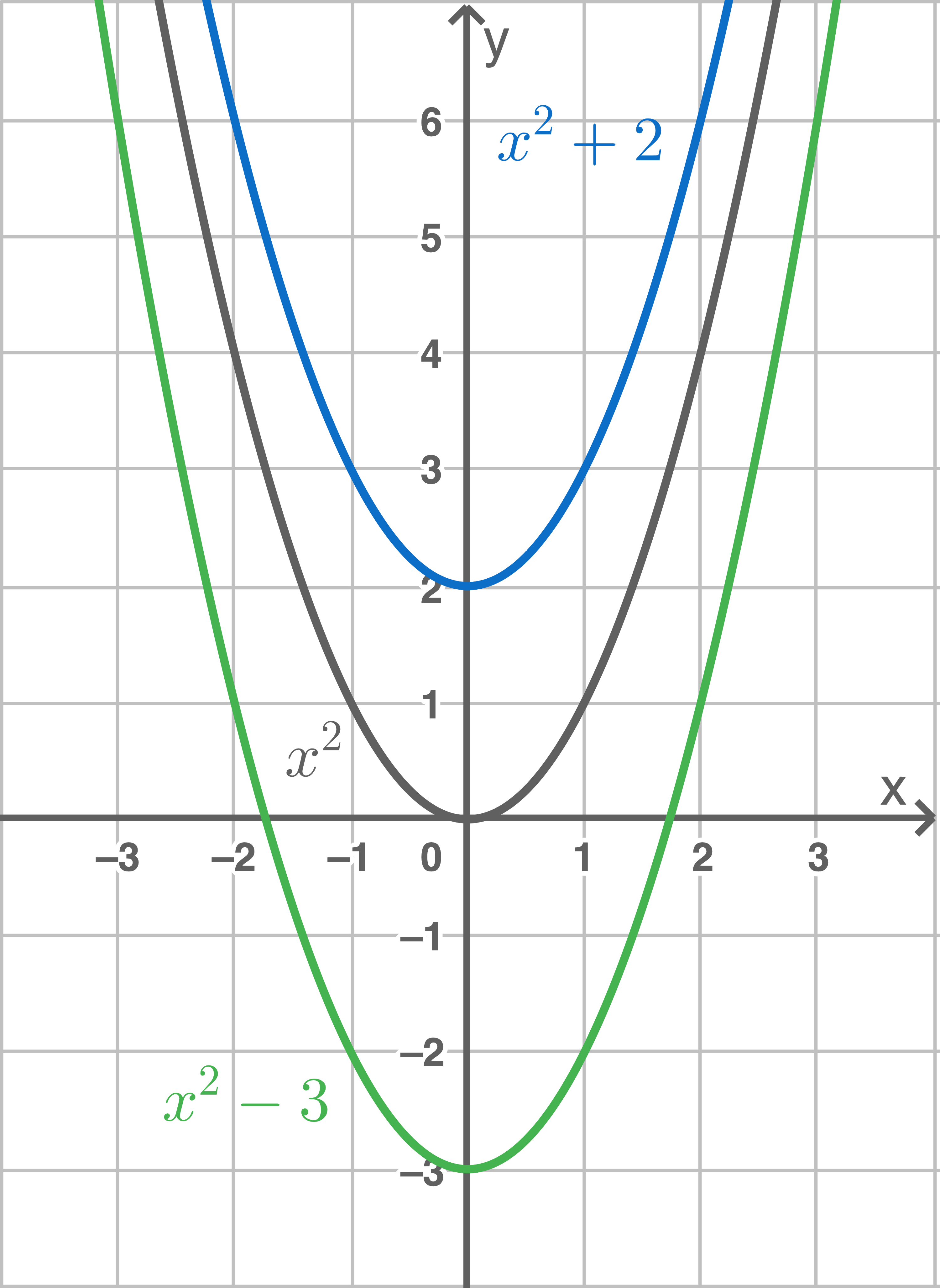
Verschieben der Normalparabel in y-Richtung
Der Graph einer verschobenen Normalparabel der Form 
ergibt sich, indem der Graph der Normalparabel um 
Einheiten entlang der 
-Achse verschoben wird:
Auch die Anzahl der Nullstellen der Funktion hängt vom Wert 
ab:
Verschiebung nach oben
Verschiebung nach unten
genau eine Nullstelle
1
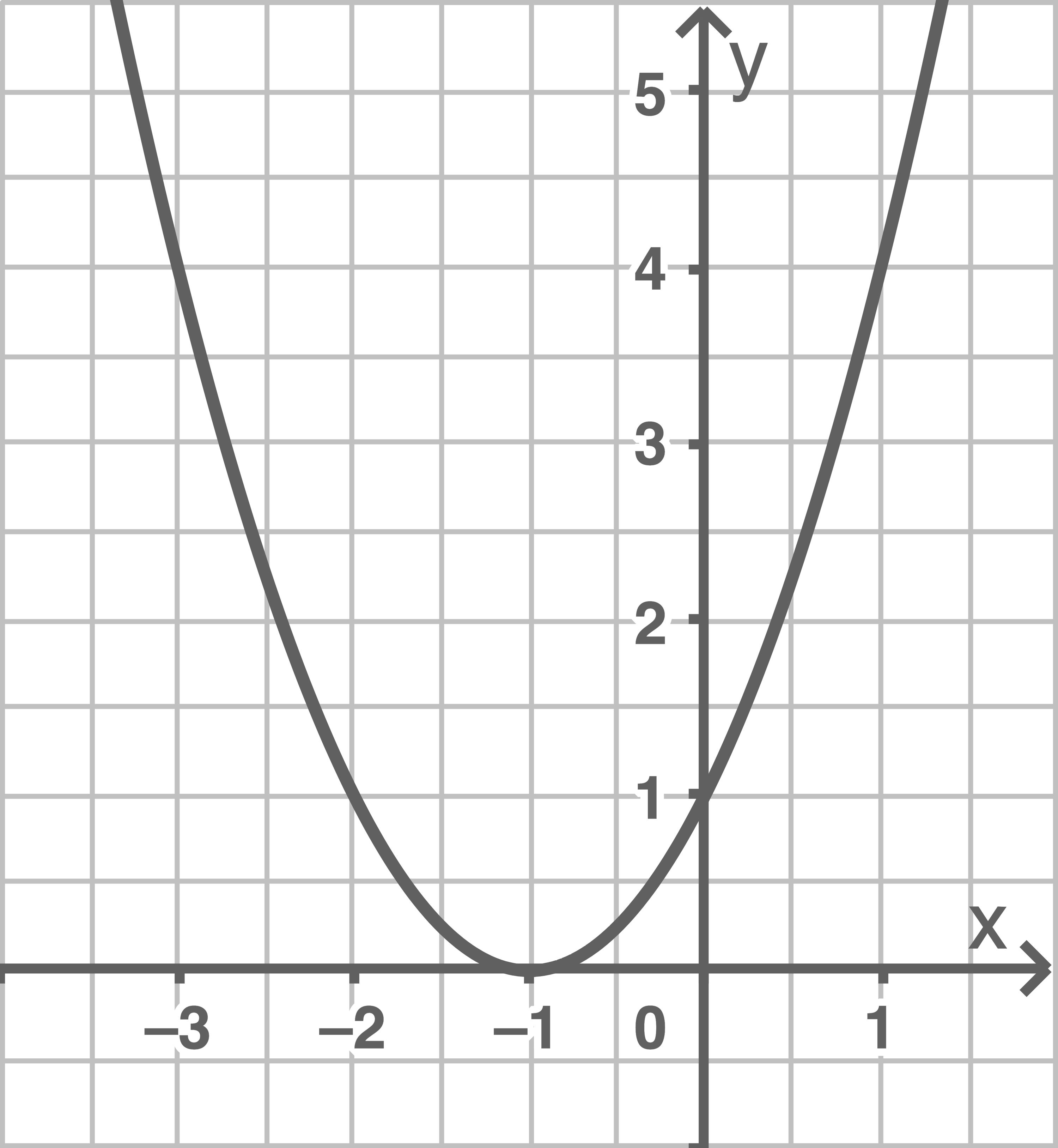
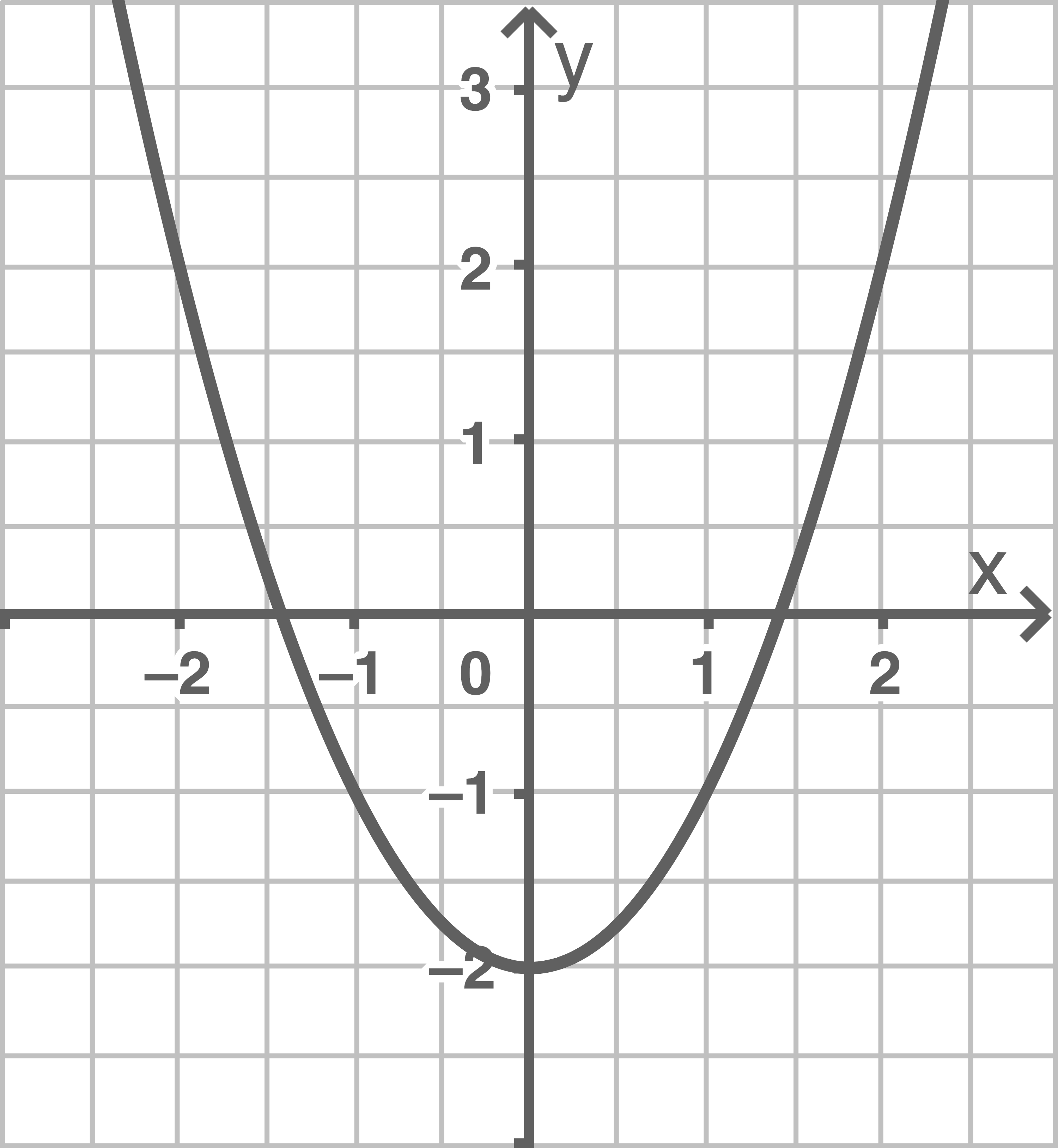
Zeichne den Graphen der Funktion und gib die Koordinaten des Scheitelpunkts an.
a)
b)
c)
d)
2
Gib die Gleichung einer in 
-Richtung verschobenen Normalparabel an, die die angegebene Eigenschaft hat.
Der Graph der Normalparabel wird nun in 
-Richtung verschoben. Gib wieder die zugehörige Gleichung an.
a)
Die Symmetrieachse des Graphen hat die Gleichung 
b)
Der Graph ist monoton fallend für 
und monoton steigend für 
c)
Der kleinste Wert ist 
d)
Der Scheitelpunkt hat die Koordinaten 
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
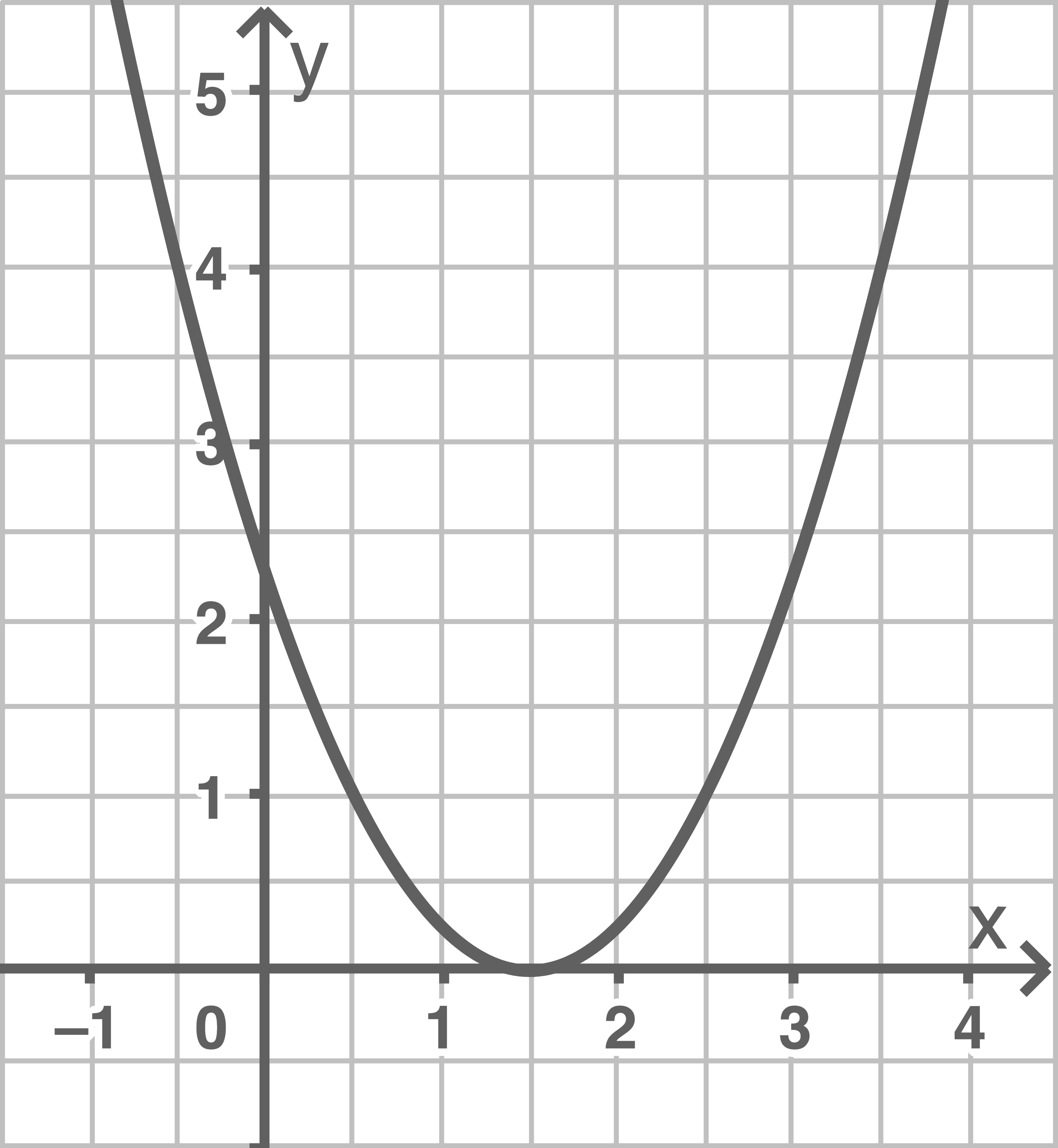
d)
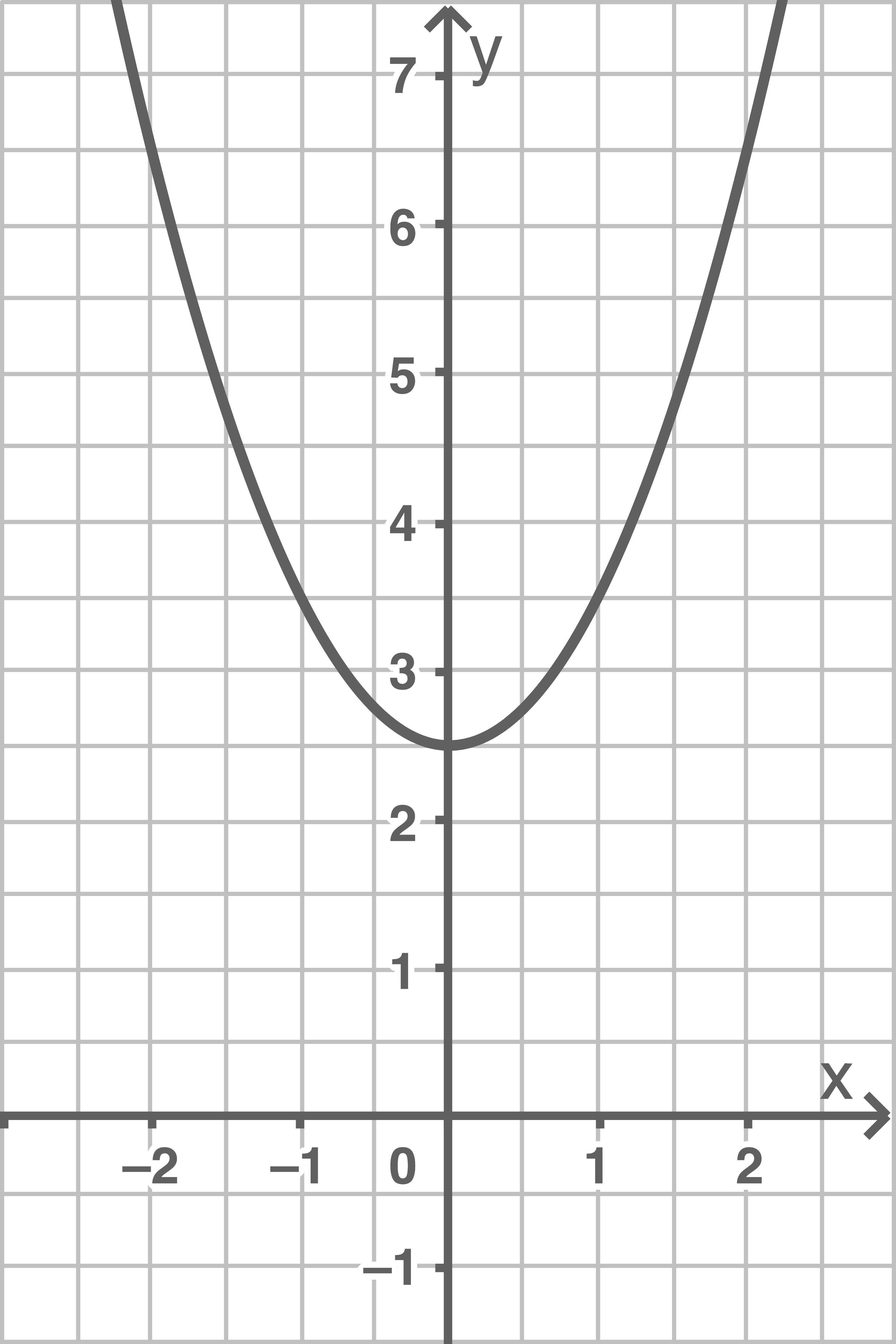
2
a)
b)
c)
d)