Höhen- und Kathetensatz
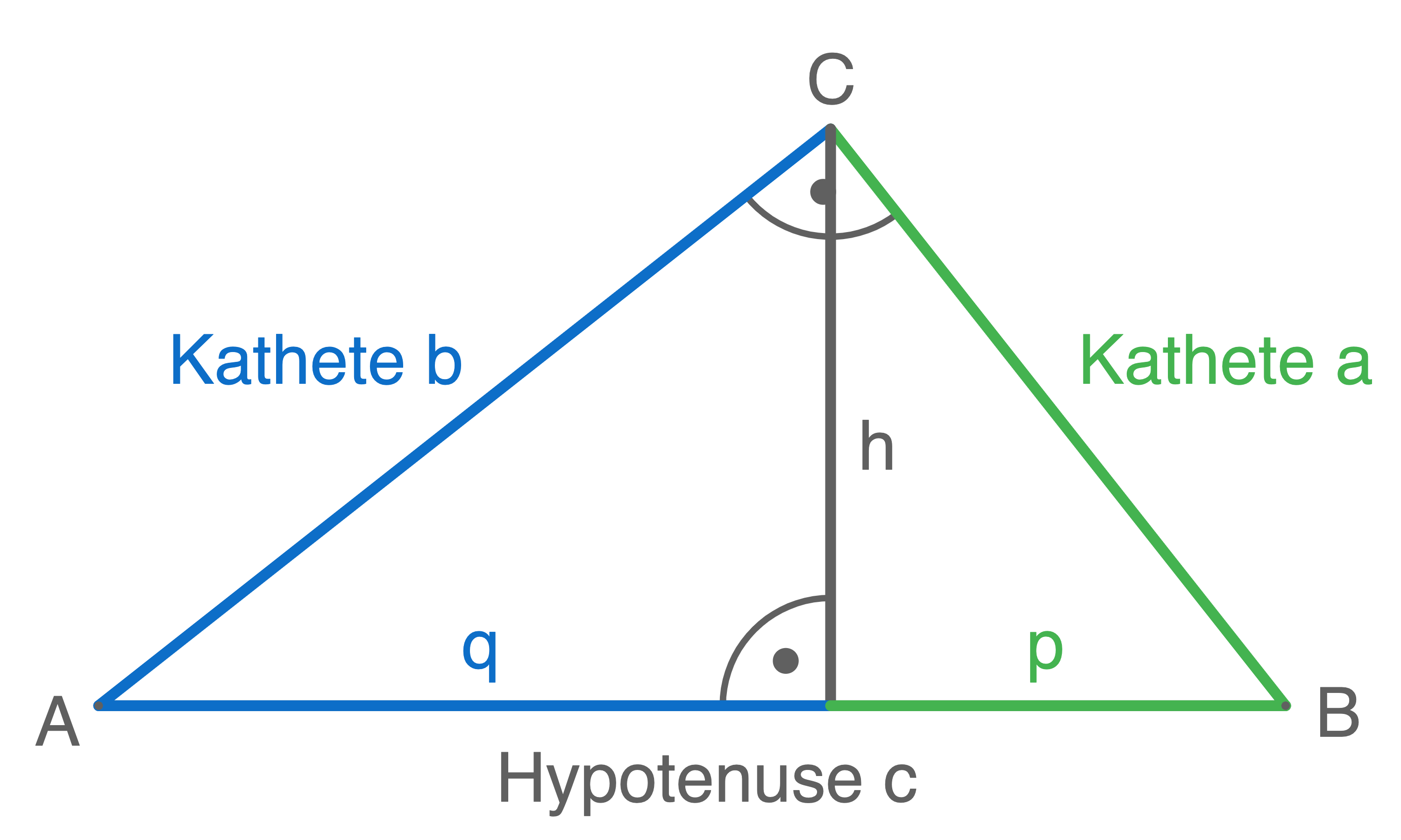
Die Höhe 
eines rechtwinkligen Dreiecks teilt die Hypotenuse in zwei Hypotenusenabschnitte 
und 
so ist das Dreieck rechtwinklig.
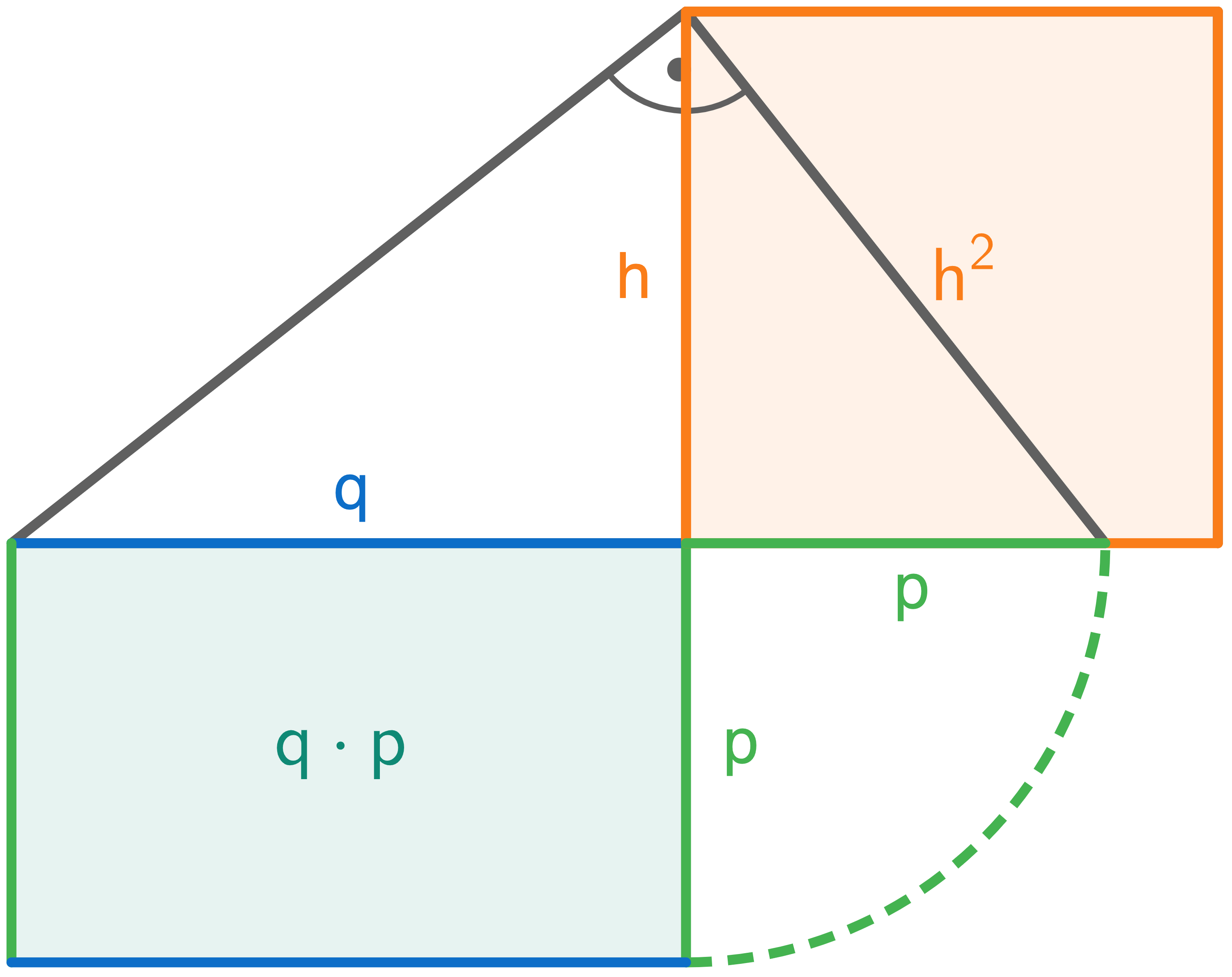
Höhensatz des Euklid
In einem rechtwinkligen Dreieck hat das Höhenquadrat denselben Flächeninhalt wie das Rechteck aus den zugehörigen Hypotenusenabschnitten:
Umkehrung des Höhensatzes
Hat das Höhenquadrat in einem Dreieck denselben Flächeninhalt wie das Rechteck aus den zugehörigen Hypotenuseabschnitten, gilt alsoKathetensatz des Euklid
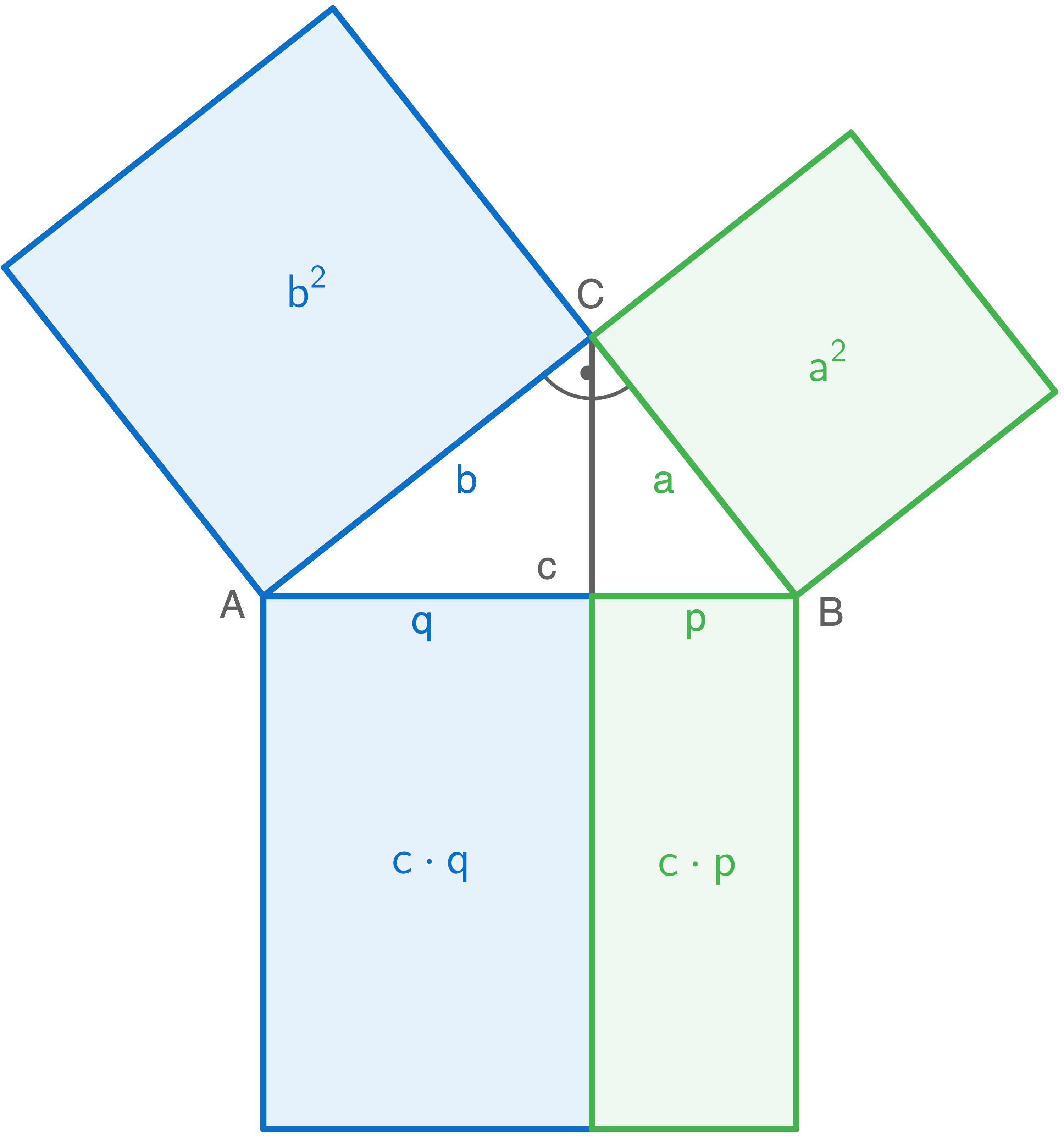
In einem rechtwinkligen Dreieck hat das Quadrat über einer Kathete denselben Flächeninhalt wie das Rechteck aus der Hypotenuse und dem zugehörigen Hypotenusenabschnitt. Mit 
gilt:
oder 
und 
und Hypotenuse 
mit zugehörigen Hypotenusenabschnitten und 
das Verhältnis 
oder 
so ist das Dreieck rechtwinklig.
Umkehrung des Kathetensatzes
Gilt in einem Dreieck mit den Katheten
1
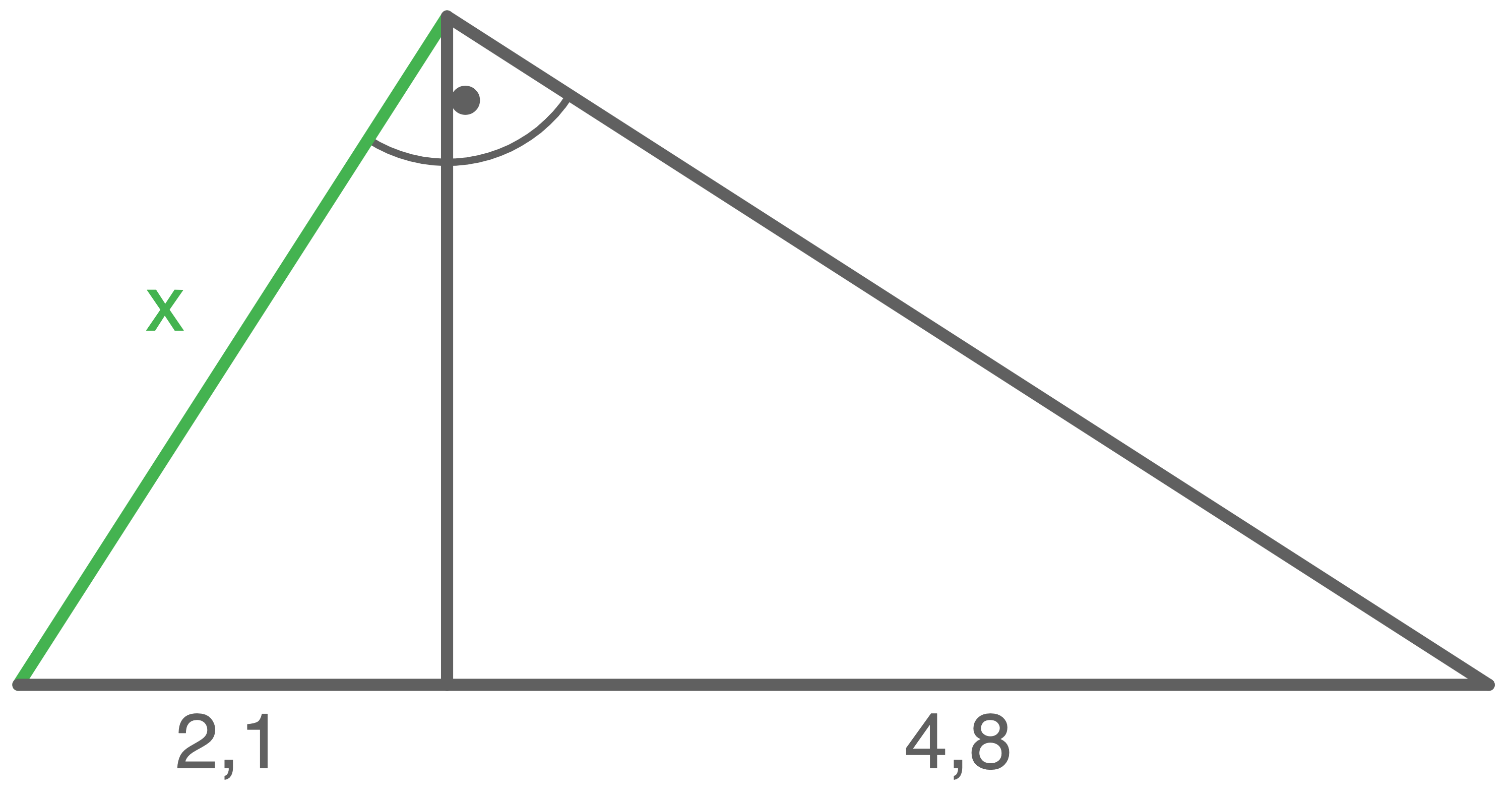
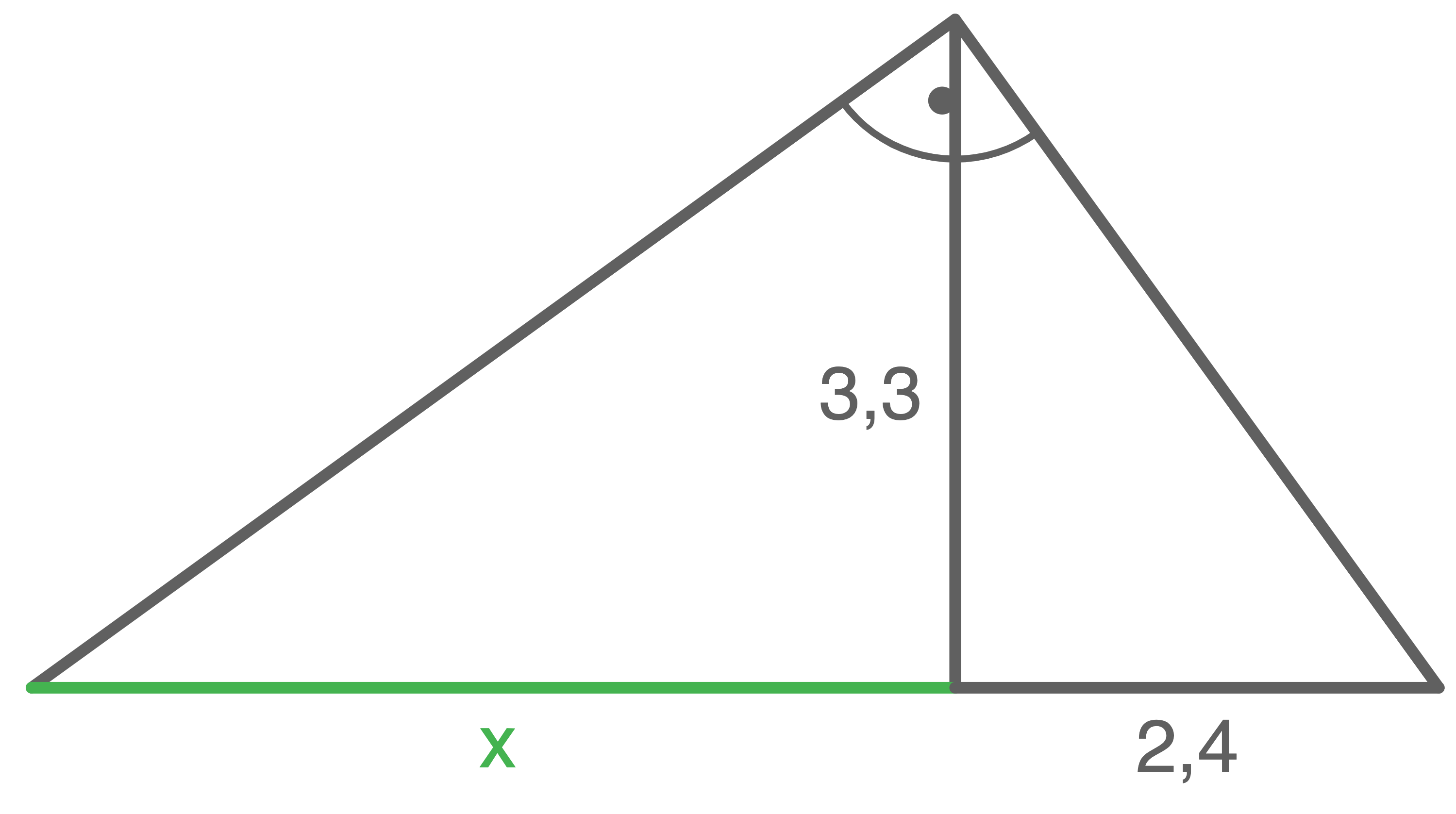
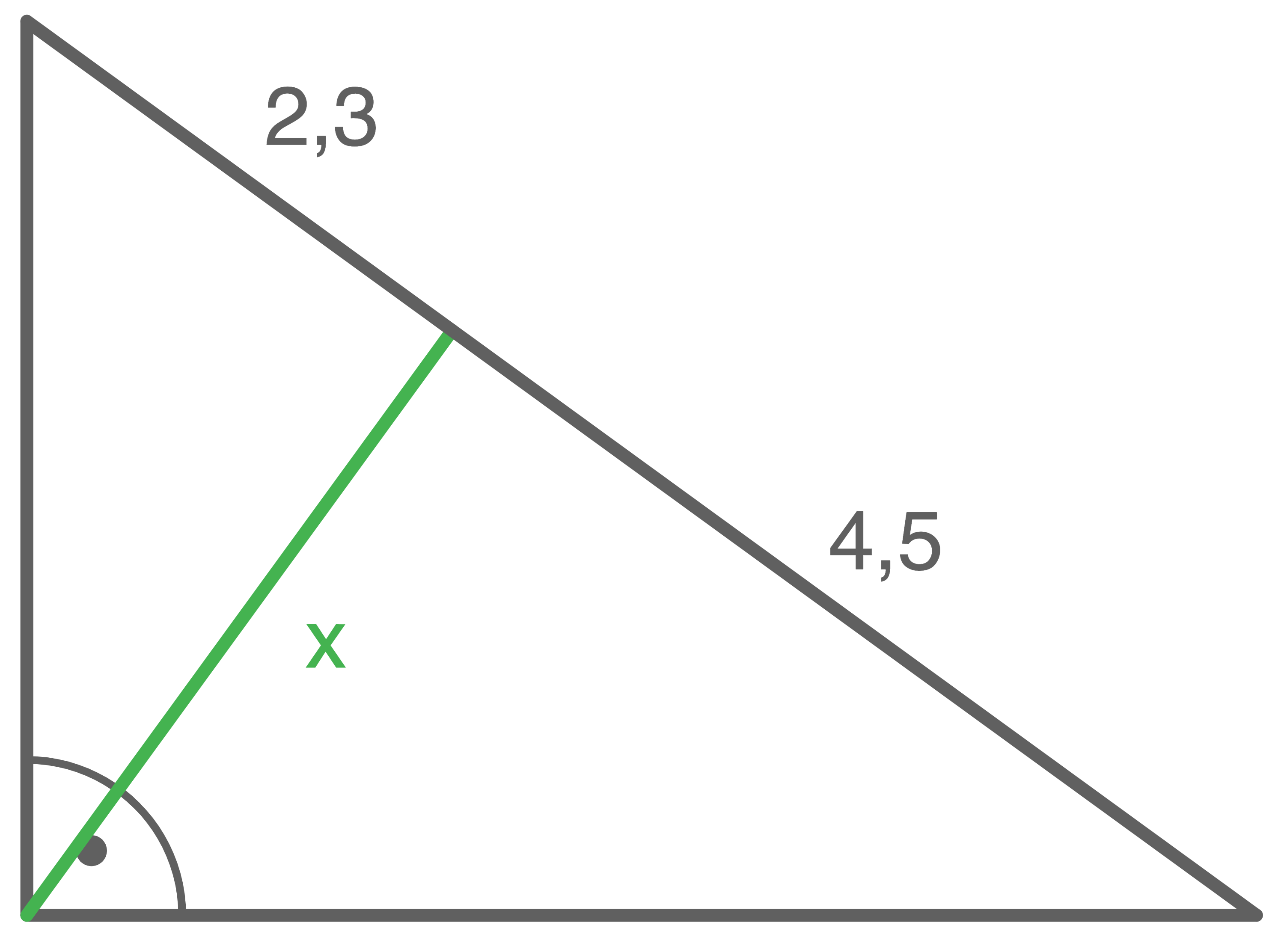
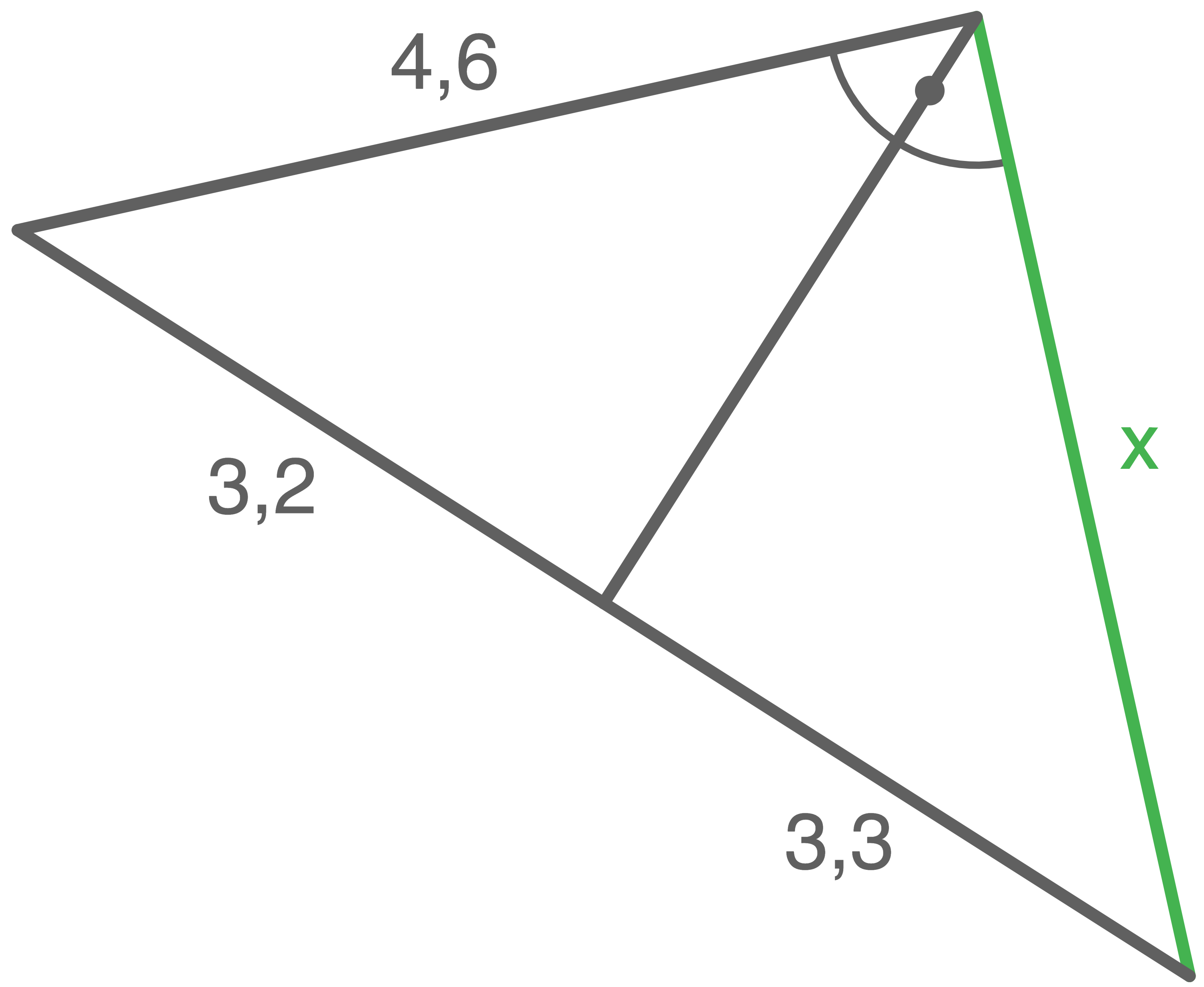
Berechne die Länge 
der grün markierten Strecke.
a)
b)
c)
d)
2
Prüfe, ob es sich um ein rechtwinkliges Dreieck handelt.
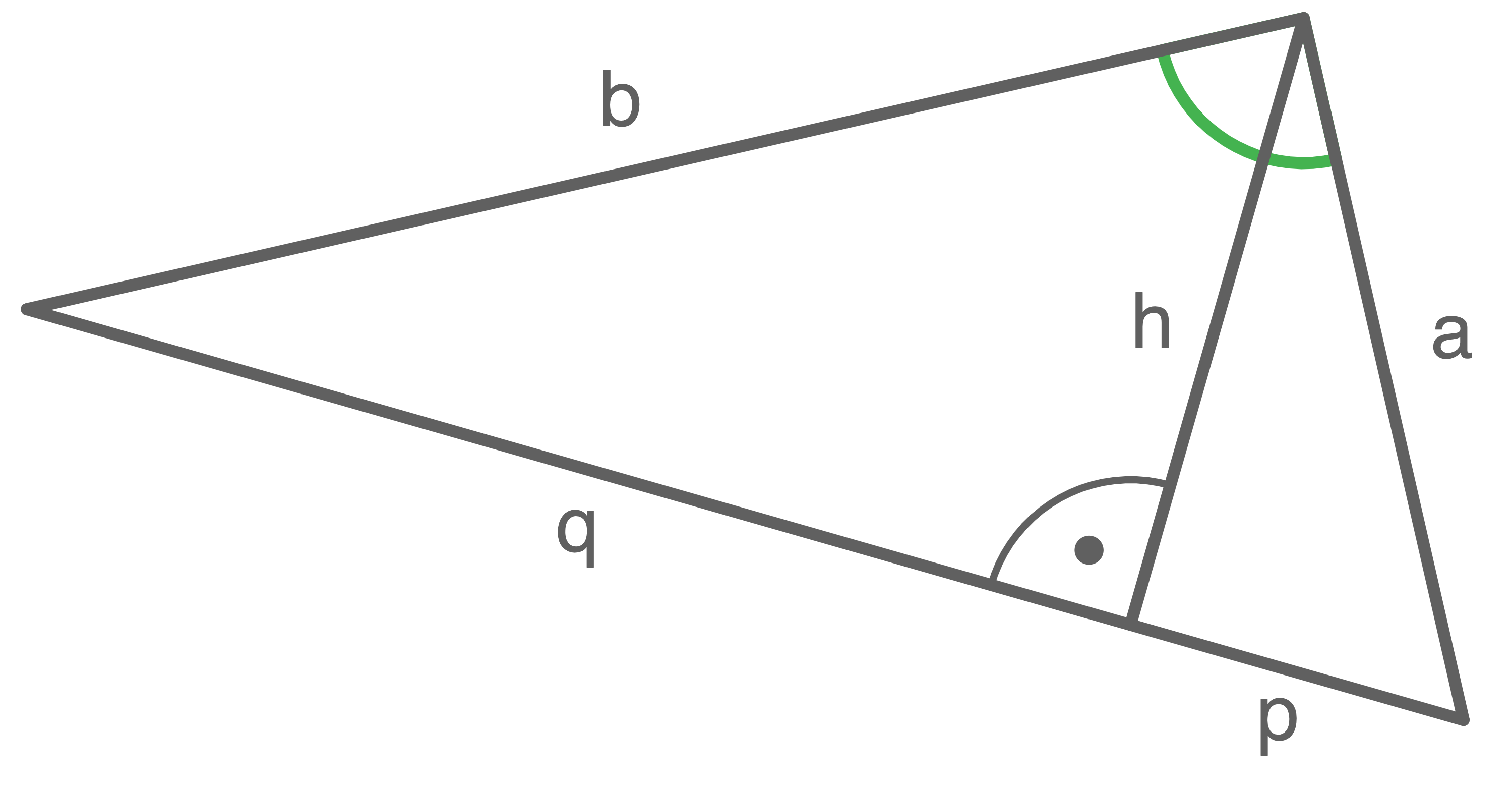
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Mit dem Kathetensatz gilt:
![\(\begin{array}[t]{rll}
x^2&=& (2,1+4,8)\cdot 2,1 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
x&=& \sqrt{(2,1+4,8)\cdot 2,1} \\[5pt]
x&\approx& 3,8
\end{array}\)](https://mathjax.schullv.de/78add815607609773f1993bbd877cd4192586d1a3298600e2bfa332c6dfd70b5?color=5a5a5a)
b)
Mit dem Höhensatz gilt:
![\(\begin{array}[t]{rll}
x\cdot 2,4&=& (3,3)^2 \quad \scriptsize \mid\; :2,4 \\[5pt]
x&=& \dfrac{3,3^2}{2,4} \\[5pt]
x &\approx& 4,5
\end{array}\)](https://mathjax.schullv.de/4d25ce1cb7ad51d92b7af20fef9f5074b38351e3e5bb3c7294e989826651d759?color=5a5a5a)
c)
Mit dem Höhensatz gilt:
![\(\begin{array}[t]{rll}
x^2&=& 2,3\cdot 4,5 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
x&=& \sqrt{2,3\cdot 4,5}\\[5pt]
x&\approx& 3,2
\end{array}\)](https://mathjax.schullv.de/e6d306fc6984b7dc17e22fb88fba75f9b05e9dd04de67c53ebd8436bf24dac33?color=5a5a5a)
d)
Mit dem Kathetensatz gilt:
![\(\begin{array}[t]{rll}
x^2&=& (3,2+3,3)\cdot 3,3 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
x&=& \sqrt{(3,2+3,3)\cdot 3,3} \\[5pt]
x&\approx& 4,6
\end{array}\)](https://mathjax.schullv.de/f5b22f5b6dc6e8878ec117b72553b075f5f0f8757b679081fae2b88833674450?color=5a5a5a)
2
a)
Umkehrung des Höhensatzes anwenden:
![\(\begin{array}[t]{rll}
h^2&=& q\cdot p \\[5pt]
(3,09\,\text{cm})^2&=& 5,6\,\text{cm}\cdot 1,7\,\text{cm} \\[5pt]
9,5\,\text{cm}^2&=& 9,5\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/aadc54006fc03e9321bee8d3418afe71eee4095d19c8c1f2b9aa1456f42ea524?color=5a5a5a)
Das Dreick ist rechtwinklig.
b)
Umkehrung des Kathetensatzes anwenden:
![\(\begin{array}[t]{rll}
b^2&=& c\cdot p \\[5pt]
(6,12\,\text{cm})^2&=& (5,1\,\text{cm}+1,3\,\text{cm})\cdot 5,1\,\text{cm} \\[5pt]
37,5\,\text{cm}^2&\neq& 32,6\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/debadb8ef02d2937201185f5a131de2d8fff1088d02e4bae7caf67d500ebf0d7?color=5a5a5a)
Das Dreieck ist nicht rechtwinklig.
c)
Umkehrung des Kathetensatzes anwenden:
![\(\begin{array}[t]{rll}
a^2&=& c\cdot p \\[5pt]
(3,3\,\text{cm})^2&=& (4,7\,\text{cm}+1,7\,\text{cm})\cdot 1,7\,\text{cm} \\[5pt]
10,9\,\text{cm}^2&=& 10,9\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/1d10d9e2df3513962d53ea6225674c72a36186e1ad172835f0e73b5ee5fba4bc?color=5a5a5a)
Das Dreieck ist rechtwinklig.
d)
Umkehrung des Höhensatzes anwenden:
![\(\begin{array}[t]{rll}
h^2&=& q\cdot p \\[5pt]
(7,7\,\text{cm})^2&=& 12,2\,\text{cm}\cdot 4,1\,\text{cm} \\[5pt]
52,3\,\text{cm}^2&\neq& 50\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/cd035a8a51b42b263d9264ac02b765bab48117dcc902620323ad3bce1049acf0?color=5a5a5a)
Das Dreieck ist nicht rechtwinklig.