Extremwertaufgaben
Vorgehensweise
1. Sachverhalt veranschaulichen 2. Funktionsterm aufstellen 3. Funktionswert bestimmen 4. Extrempunkt bestimmen 5. Ränder des Definitionsbereiches vergleichen 6. Ergebnis prüfen 7. Ergebnis formulierenBeispiel
An eine Hauswand angrenzend soll ein rechteckiger Stellplatz für Fahrräder eingezäunt werden. Im Baumarkt hat Anna einen 12 Meter langen Zaun gekauft. Der Stellplatz soll möglichst groß werden. 1. Schritt: Sachverhalt veranschaulichen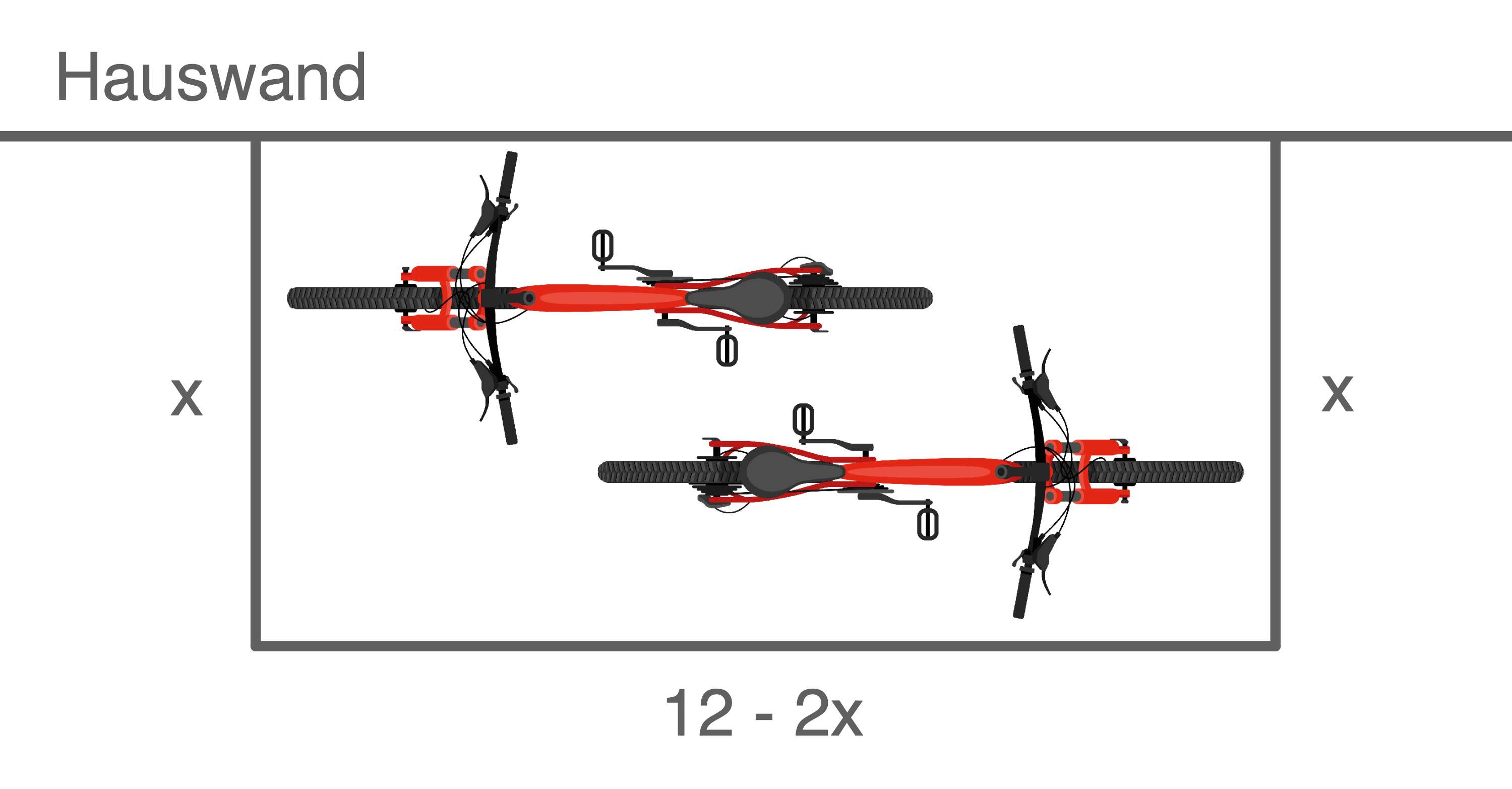
1
Eine  lange Schnur wird als Rechteck ausgelegt. Eine Seitenlänge ist
lange Schnur wird als Rechteck ausgelegt. Eine Seitenlänge ist  Bestimme
Bestimme  so, dass der Flächeninhalt
so, dass der Flächeninhalt
a)
...mindestens  groß ist.
groß ist.
b)
...genau  groß ist.
groß ist.
c)
...am größten ist.
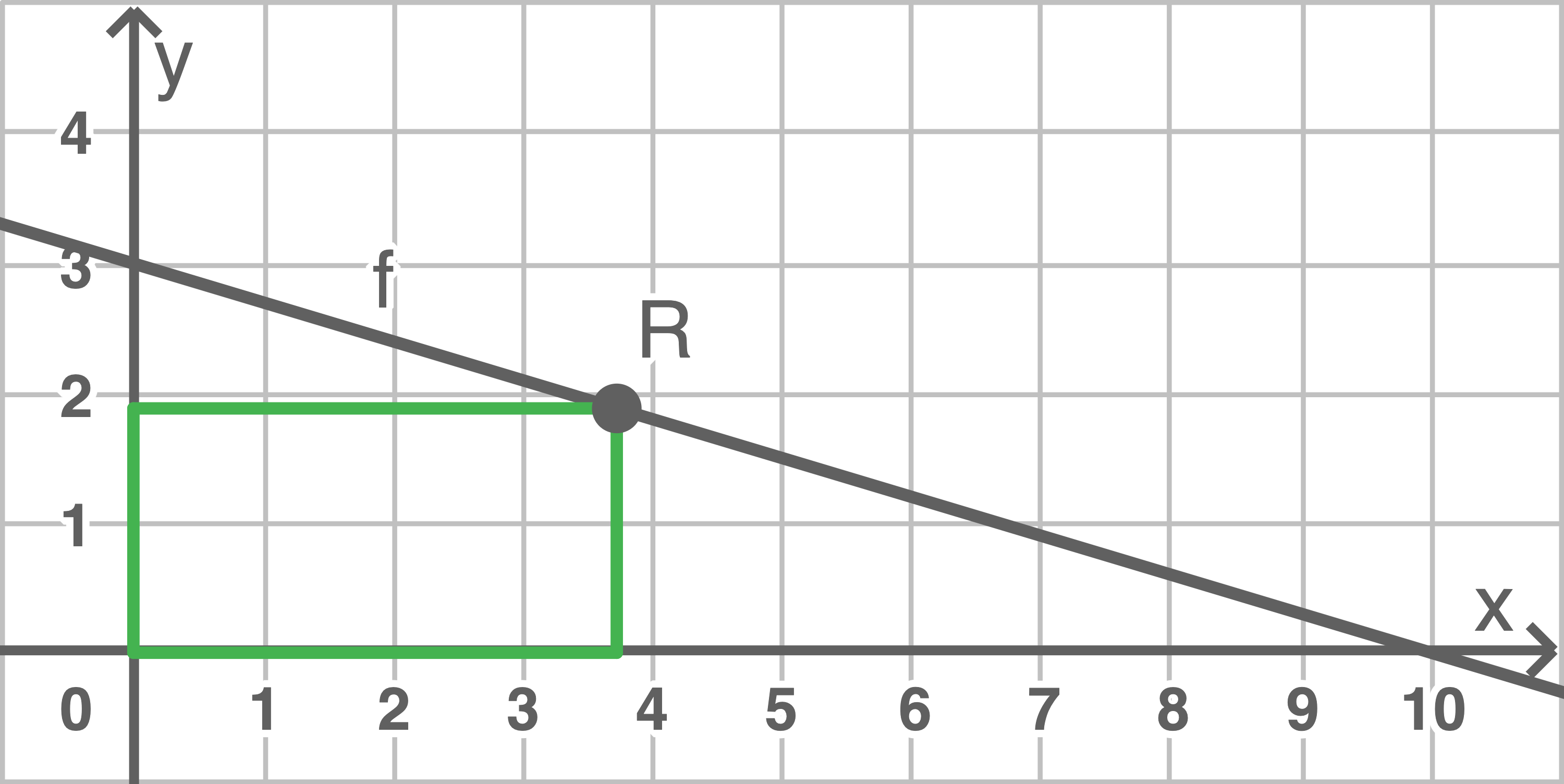
2
Für welchen Punkt  der auf der Geraden mit der Gleichung
der auf der Geraden mit der Gleichung  liegt, hat das Rechteck mit den Eckpunkten
liegt, hat das Rechteck mit den Eckpunkten  und
und  den größten Flächeninhalt?
den größten Flächeninhalt?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
1. Schritt: Sachverhalt veranschaulichen
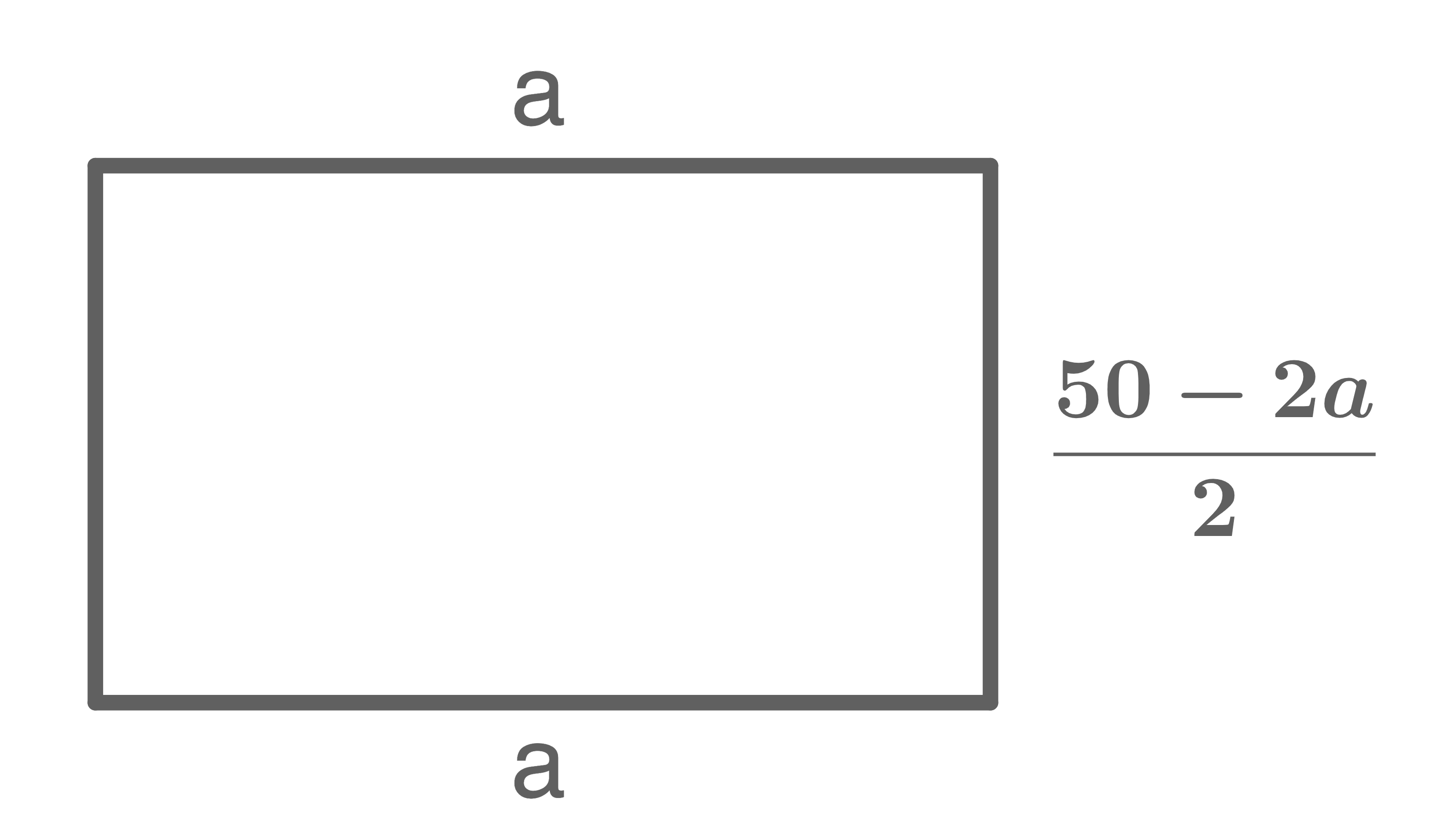 2. Schritt: Funktionsterm aufstellen
2. Schritt: Funktionsterm aufstellen


 für
für 

a)
3. Schritt: Funktionswert bestimmen
Es soll  sein.
4. Schritt: Extrempunkt bestimmen
sein.
4. Schritt: Extrempunkt bestimmen
![\(\begin{array}[t]{rll}
f(a)&\geq& 40 \\[5pt]
25a-a^2&\geq& 40
\end{array}\)](https://mathjax.schullv.de/c62ee760f2408a1015de7ac039212b60139ec0397242e466005f4b42a5fc2b4a?color=5a5a5a) Mit dem solve-Befehl des CAS folgen
Mit dem solve-Befehl des CAS folgen  und
und  5. Schritt: Ränder des Definitionsbereiches vergleichen
Für
5. Schritt: Ränder des Definitionsbereiches vergleichen
Für  und für
und für  ist
ist  6. Schritt: Ergebnis prüfen
Beide Ergebnisse sind sinnvoll und grenzen
6. Schritt: Ergebnis prüfen
Beide Ergebnisse sind sinnvoll und grenzen  ein.
7. Schritt: Ergebnis formulieren
Wird für die Seitenlänge
ein.
7. Schritt: Ergebnis formulieren
Wird für die Seitenlänge  ein Wert zwischen
ein Wert zwischen  und
und  gewählt, so nimmt das eingeschlossene Rechteck einen Flächeninhalt
gewählt, so nimmt das eingeschlossene Rechteck einen Flächeninhalt  an.
an.
b)
3. Schritt: Funktionswert bestimmen
Es soll  sein.
4. Schritt: Extrempunkt bestimmen
sein.
4. Schritt: Extrempunkt bestimmen
![\(\begin{array}[t]{rll}
f(a)&=& 20 \\[5pt]
25a-a^2&=& 20
\end{array}\)](https://mathjax.schullv.de/a0a08a68499595bc244d5f04b7ecd777785f6ebb9a4666bfa52d567281bee972?color=5a5a5a) Mit dem solve-Befehl des Taschenrechners folgt
Mit dem solve-Befehl des Taschenrechners folgt  und
und  5. Schritt: Ränder des Definitionsbereiches vergleichen
Für
5. Schritt: Ränder des Definitionsbereiches vergleichen
Für  und für
und für  ist
ist  6. Schritt: Ergebnis prüfen
Beide Ergebnisse sind sinnvoll.
7. Schritt: Ergebnis formulieren
Sowohl für
6. Schritt: Ergebnis prüfen
Beide Ergebnisse sind sinnvoll.
7. Schritt: Ergebnis formulieren
Sowohl für  als auch für
als auch für  nimmt das eingeschlossene Rechteck einen Flächeninhalt von
nimmt das eingeschlossene Rechteck einen Flächeninhalt von  an.
an.
c)
3. Schritt: Funktionswert bestimmen
Es soll  maximal sein. Gesucht sind die Koordinaten des Extrempunktes.
4. Schritt: Extrempunkt bestimmen
Mit dem CAS folgen die Koordinaten des Hochpunktes zu
maximal sein. Gesucht sind die Koordinaten des Extrempunktes.
4. Schritt: Extrempunkt bestimmen
Mit dem CAS folgen die Koordinaten des Hochpunktes zu  5. Schritt: Ränder des Definitionsbereiches vergleichen
Für
5. Schritt: Ränder des Definitionsbereiches vergleichen
Für  und für
und für  ist
ist  6. Schritt: Ergebnis prüfen
Die Stelle
6. Schritt: Ergebnis prüfen
Die Stelle  ist sinnvoll.
7. Schritt: Ergebnis formulieren
Für
ist sinnvoll.
7. Schritt: Ergebnis formulieren
Für  ist der Flächeninhalt des eingeschlossenen Rechtecks zu
ist der Flächeninhalt des eingeschlossenen Rechtecks zu  größtmöglich.
größtmöglich.
2
1. Schritt: Sachverhalt veranschaulichen
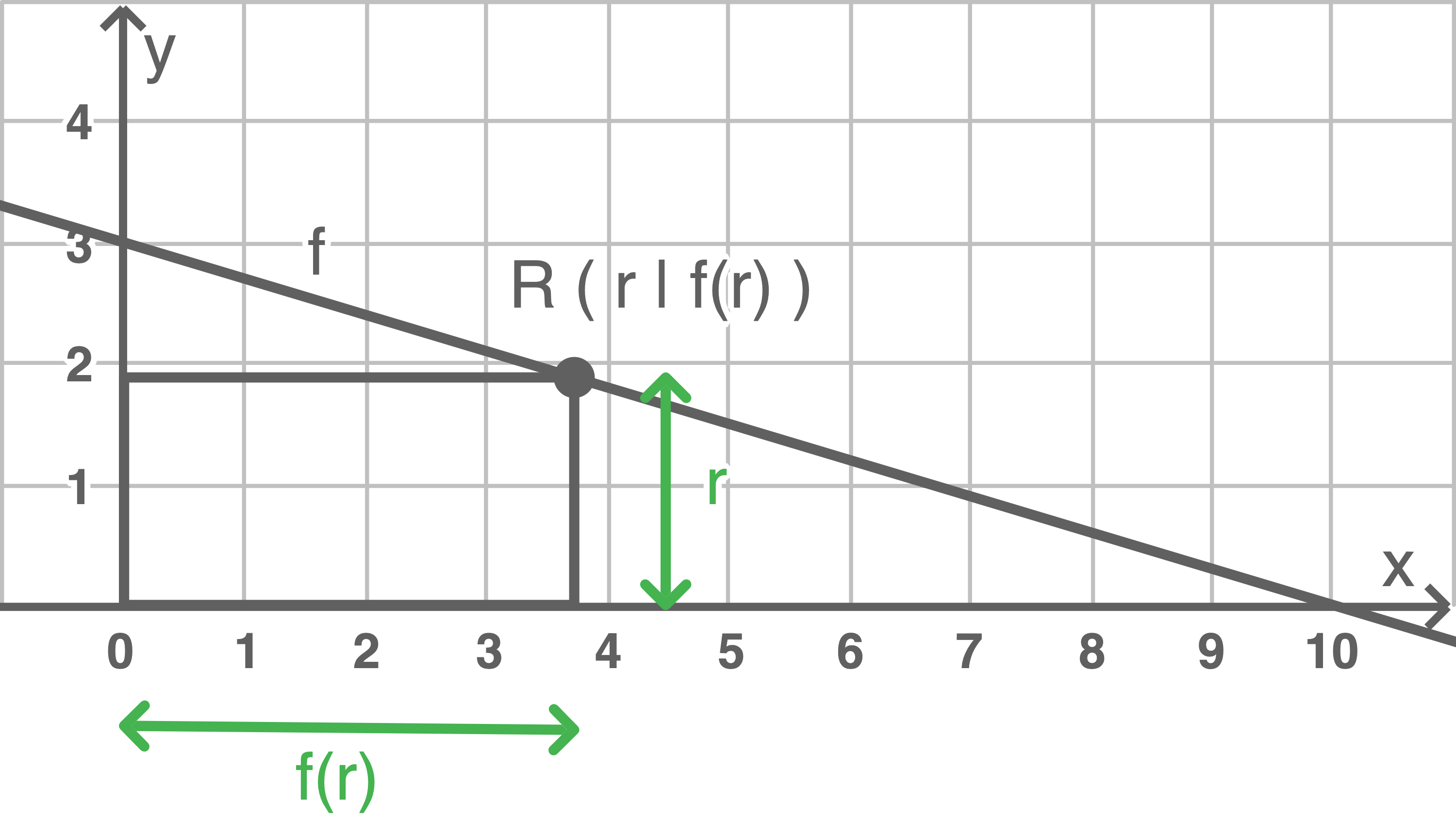 2. Schritt: Funktionsterm aufstellen
Der Inhalt der Rechtecksfläche lässt sich ausdrücken als:
2. Schritt: Funktionsterm aufstellen
Der Inhalt der Rechtecksfläche lässt sich ausdrücken als:
![\(\begin{array}[t]{rll}
A(r)&=& r\cdot f(r) \\[5pt]
&=& r \cdot \left(-\dfrac{3}{10}\cdot r+3\right) \\[5pt]
&=& -\dfrac{3}{10}\cdot r^2+3\cdot r
\end{array}\)](https://mathjax.schullv.de/36a771dd64250d4f27e67a2454113b05105a6a2355d7b9ca95b03e69a55714e0?color=5a5a5a) für
für  3. Schritt: Funktionswert bestimmen
Gesucht ist der maximale Wert von
3. Schritt: Funktionswert bestimmen
Gesucht ist der maximale Wert von  4. Schritt: Extrempunkt bestimmen
Mit dem CAS folgen die Koordinaten des Hochpunktes zu
4. Schritt: Extrempunkt bestimmen
Mit dem CAS folgen die Koordinaten des Hochpunktes zu  5. Schritt: Ränder des Definitionsbereiches vergleichen
Für
5. Schritt: Ränder des Definitionsbereiches vergleichen
Für  und für
und für  ist
ist  6. Schritt: Ergebnis prüfen
Die Stelle
6. Schritt: Ergebnis prüfen
Die Stelle  ist sinnvoll.
7. Schritt: Ergebnis formulieren
Für
ist sinnvoll.
7. Schritt: Ergebnis formulieren
Für  ist der Flächeninhalt des eingeschlossenen Rechtecks zu
ist der Flächeninhalt des eingeschlossenen Rechtecks zu  maximal.
maximal.
