Strecken und Spiegeln der Normalparabel
Strecken und Spiegeln der Normalparabel
Der Graph der Funktion mit der Gleichung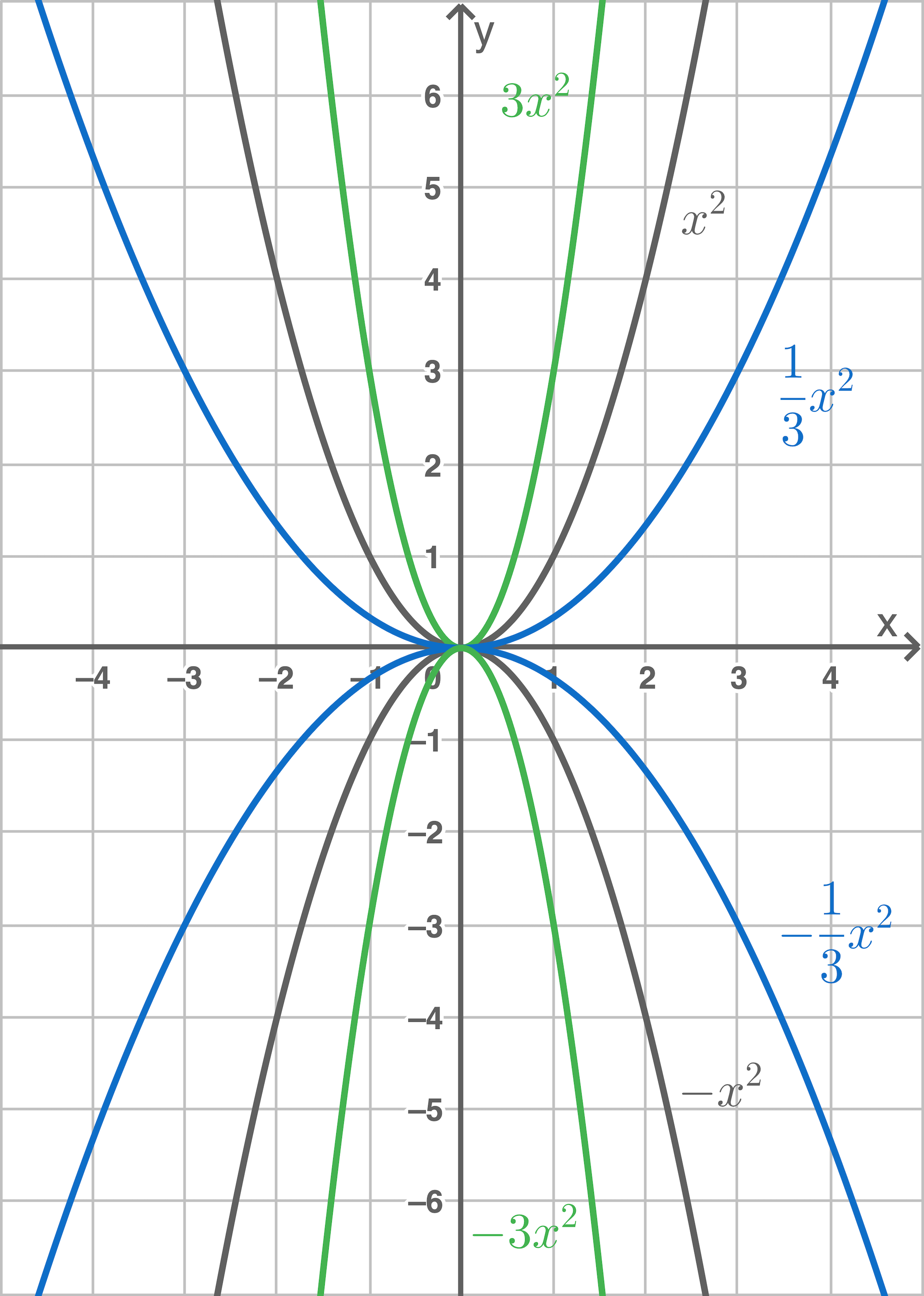
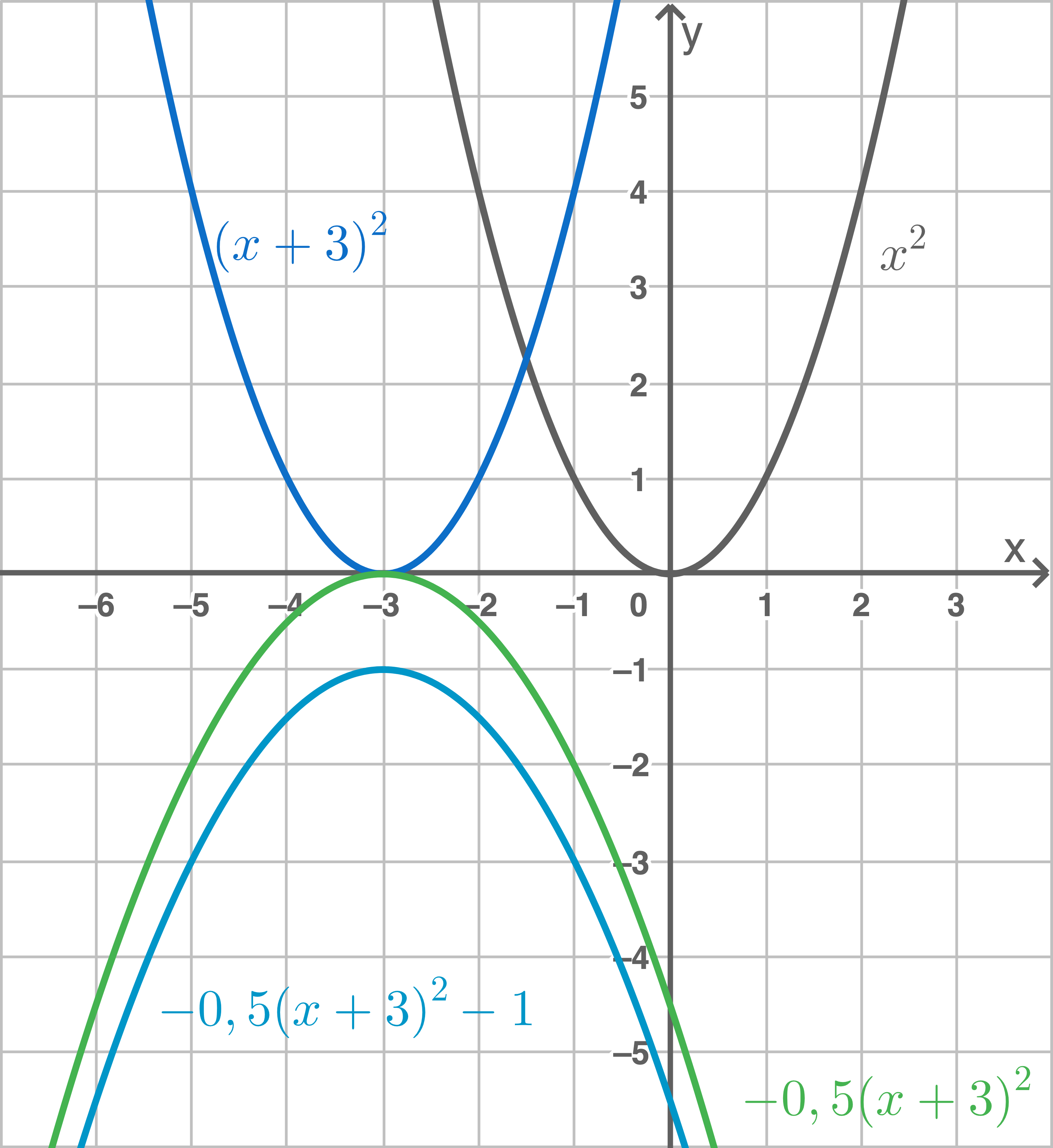
Strecken und Verschieben der Normalparabel
Der Graph einer quadratischen Funktion der Form  ergibt sich, indem die Normalparabel nacheinander
ergibt sich, indem die Normalparabel nacheinander
 Ausmultiplizieren der Klammer des Funktionsterms liefert eine Funktion in der allgemeinen Form
Ausmultiplizieren der Klammer des Funktionsterms liefert eine Funktion in der allgemeinen Form  auch quadratische Funktion genannt.
auch quadratische Funktion genannt.
- um
Einheiten entlang der
-Achse verschoben wird:
- für
nach rechts
- für
nach links
- für
- mit dem Faktor
entlang der
-Achse gestreckt wird
- um
Einheiten entlang der
-Achse verschoben wird:
- für
nach unten
- für
nach oben
- für
1
Zeichne den Graphen der angegebenen Funktion.




a)
b)
c)
d)
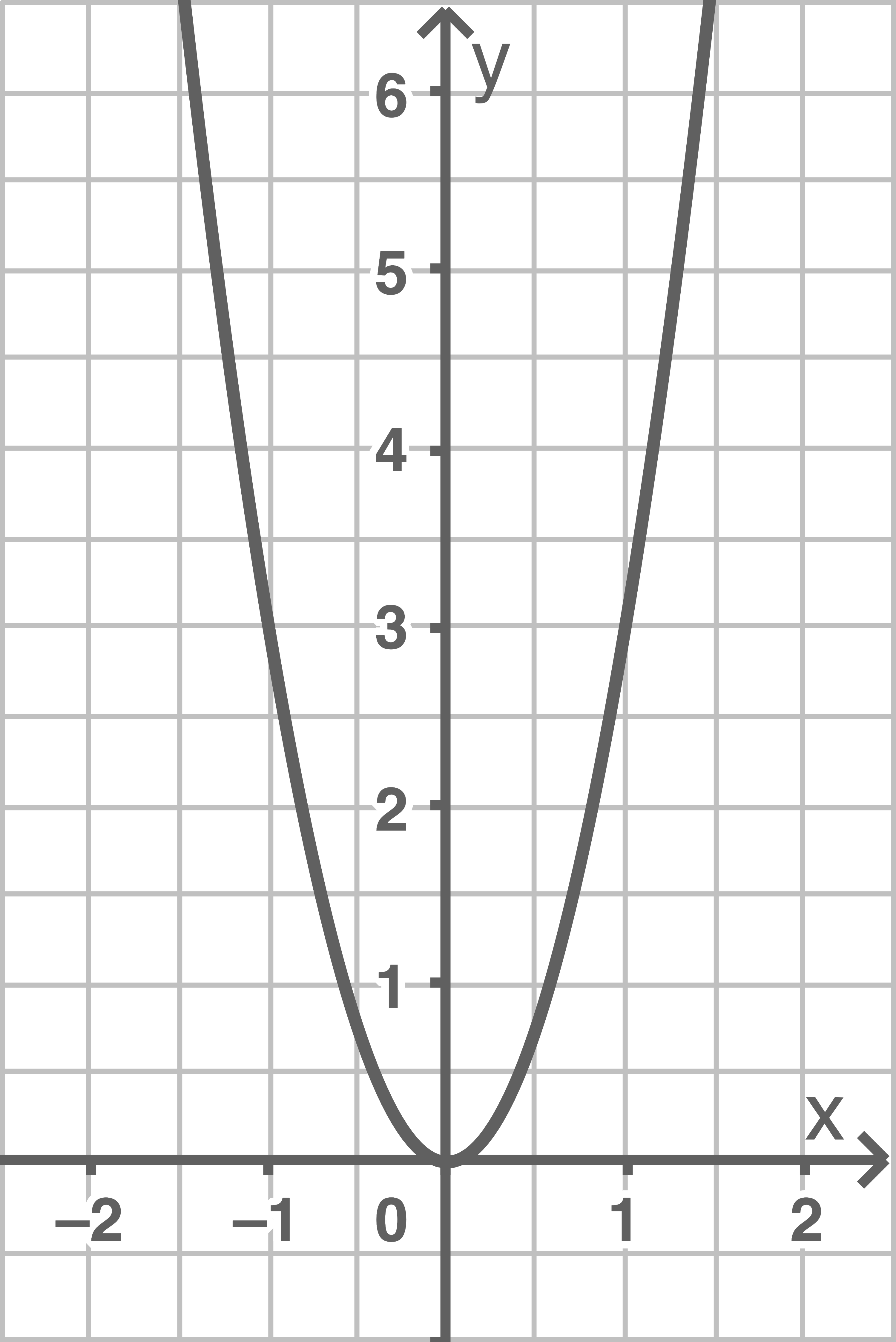
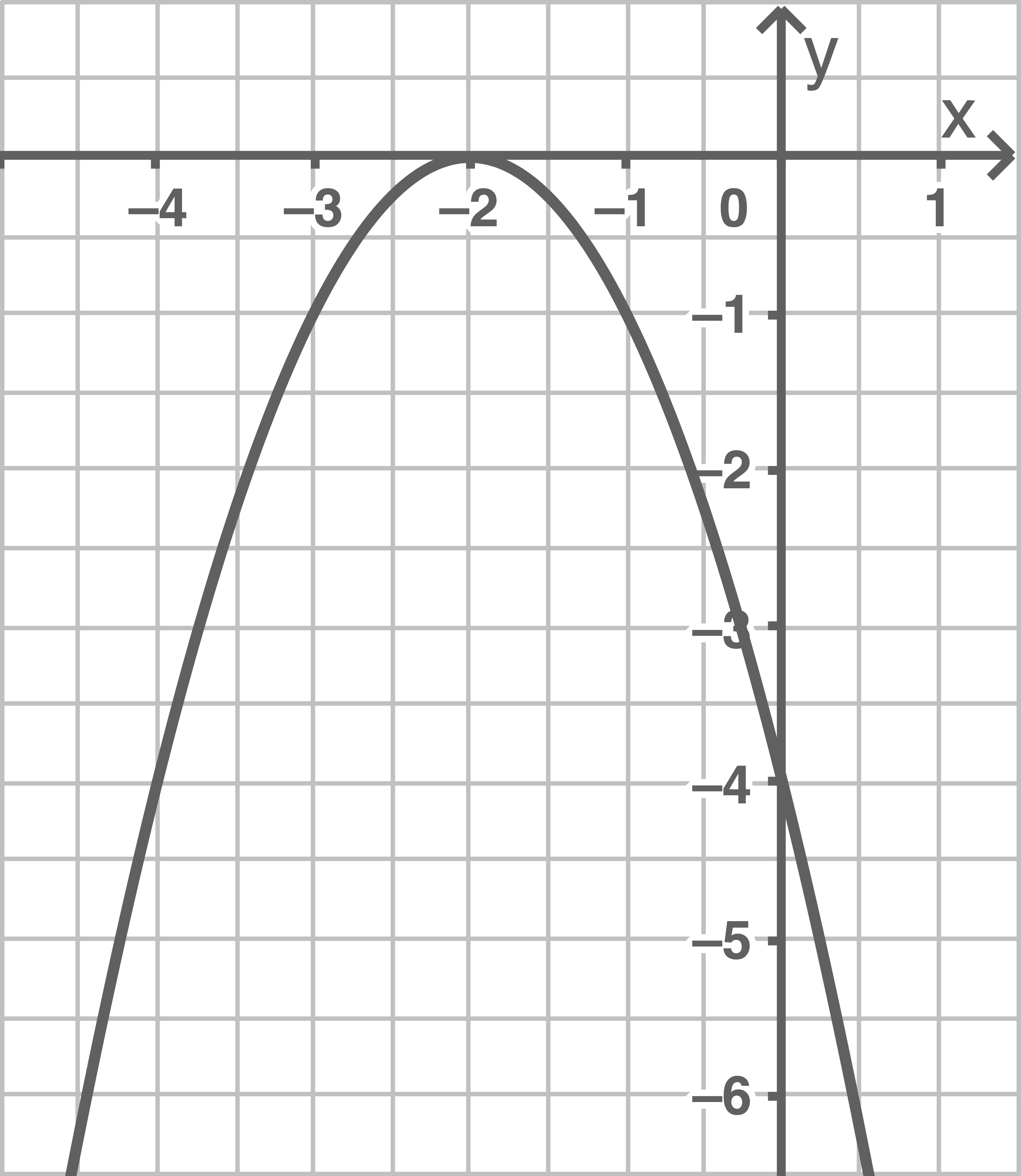
2
Gib den Funktionsterm in der Scheitelpunktform und in der allgemeinen Form an.
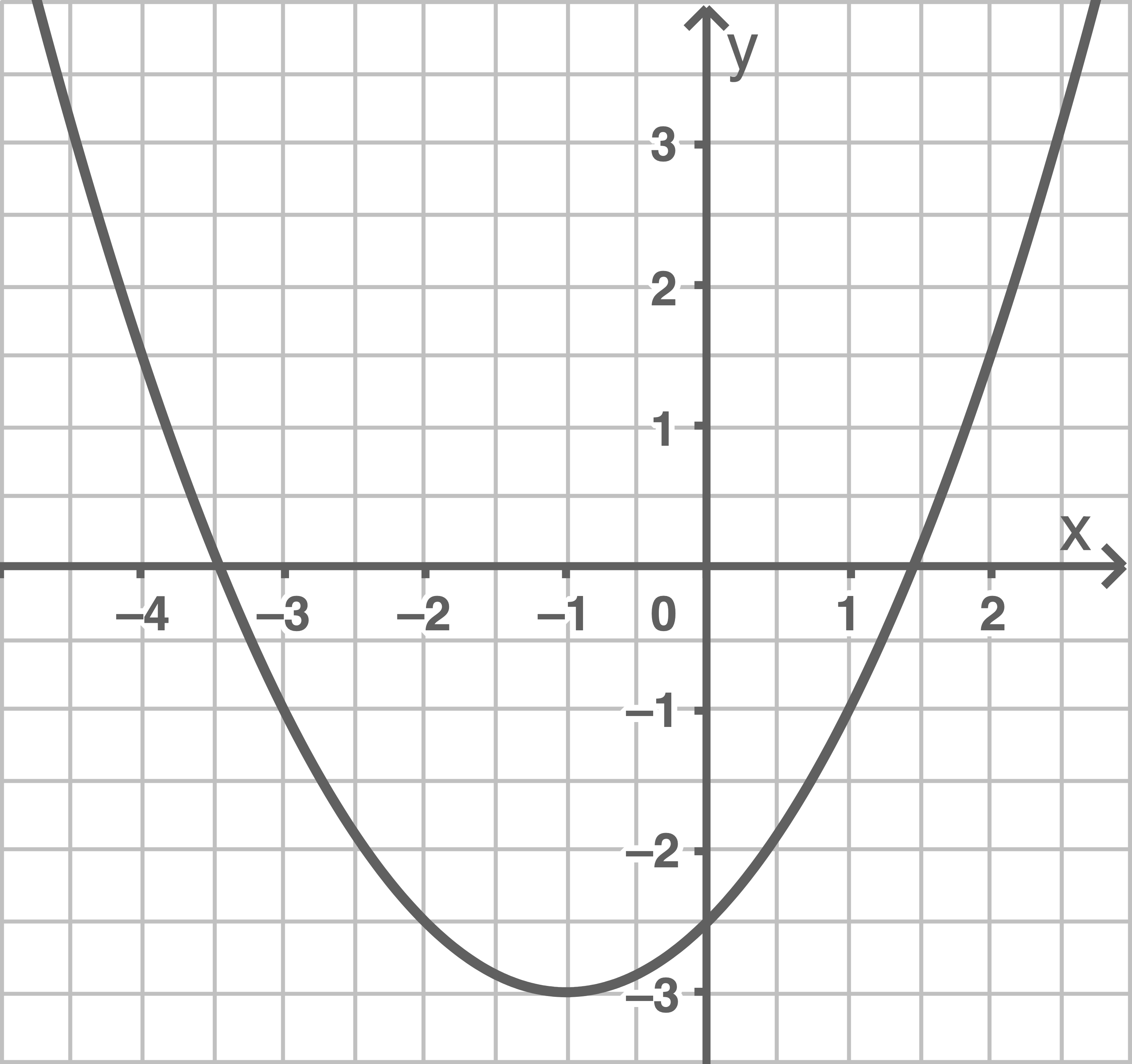
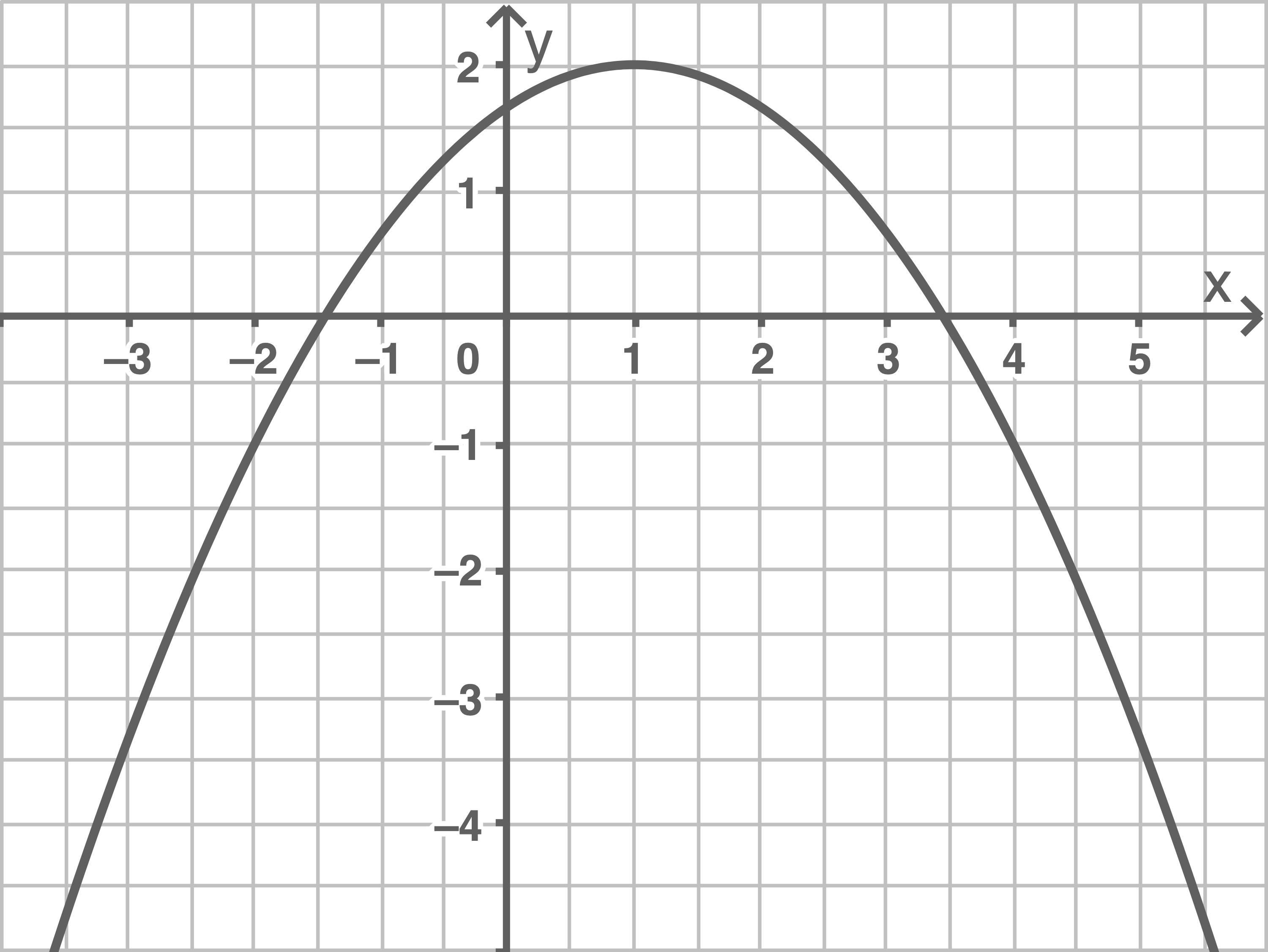
a)

b)

c)

d)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
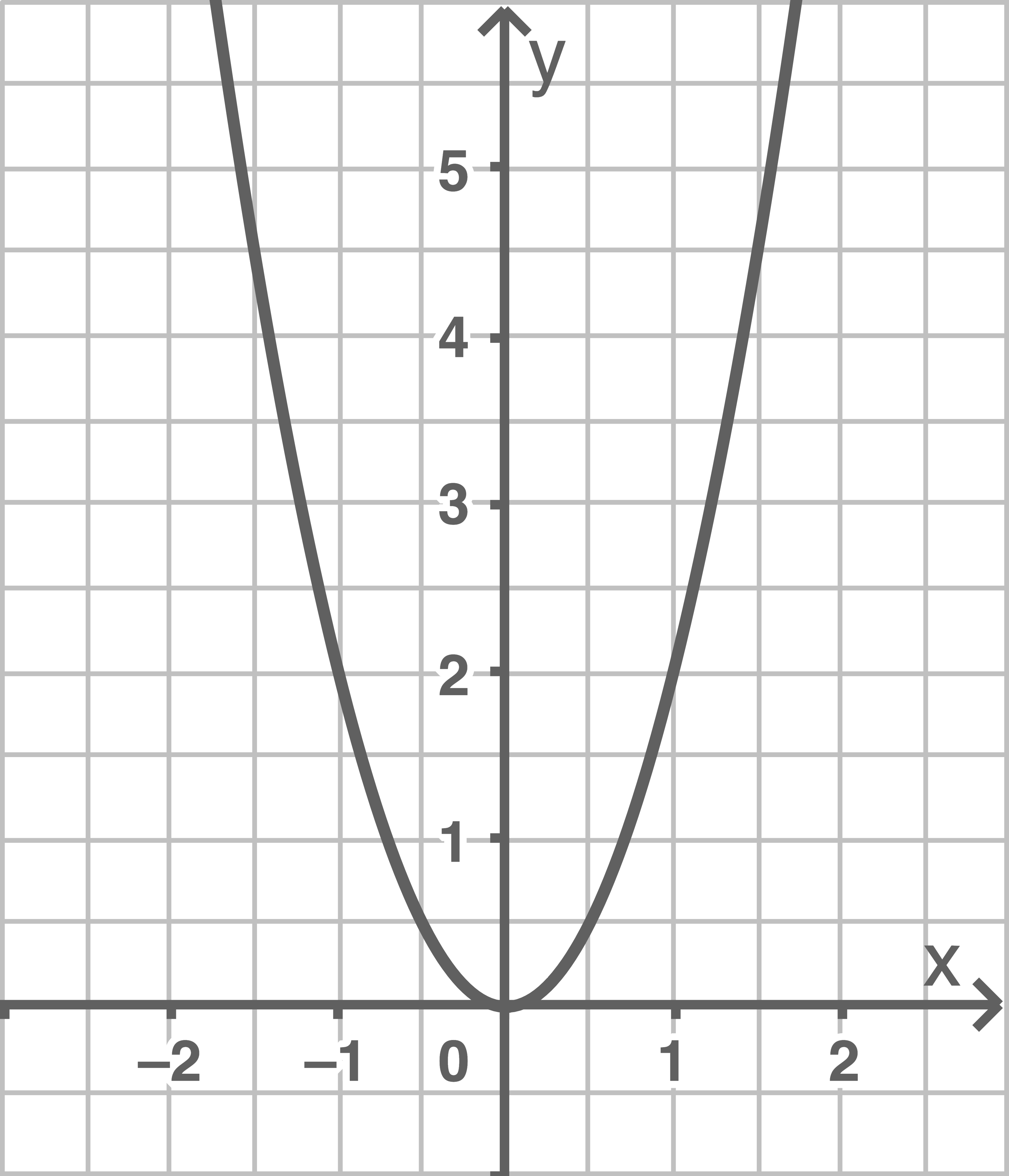
b)
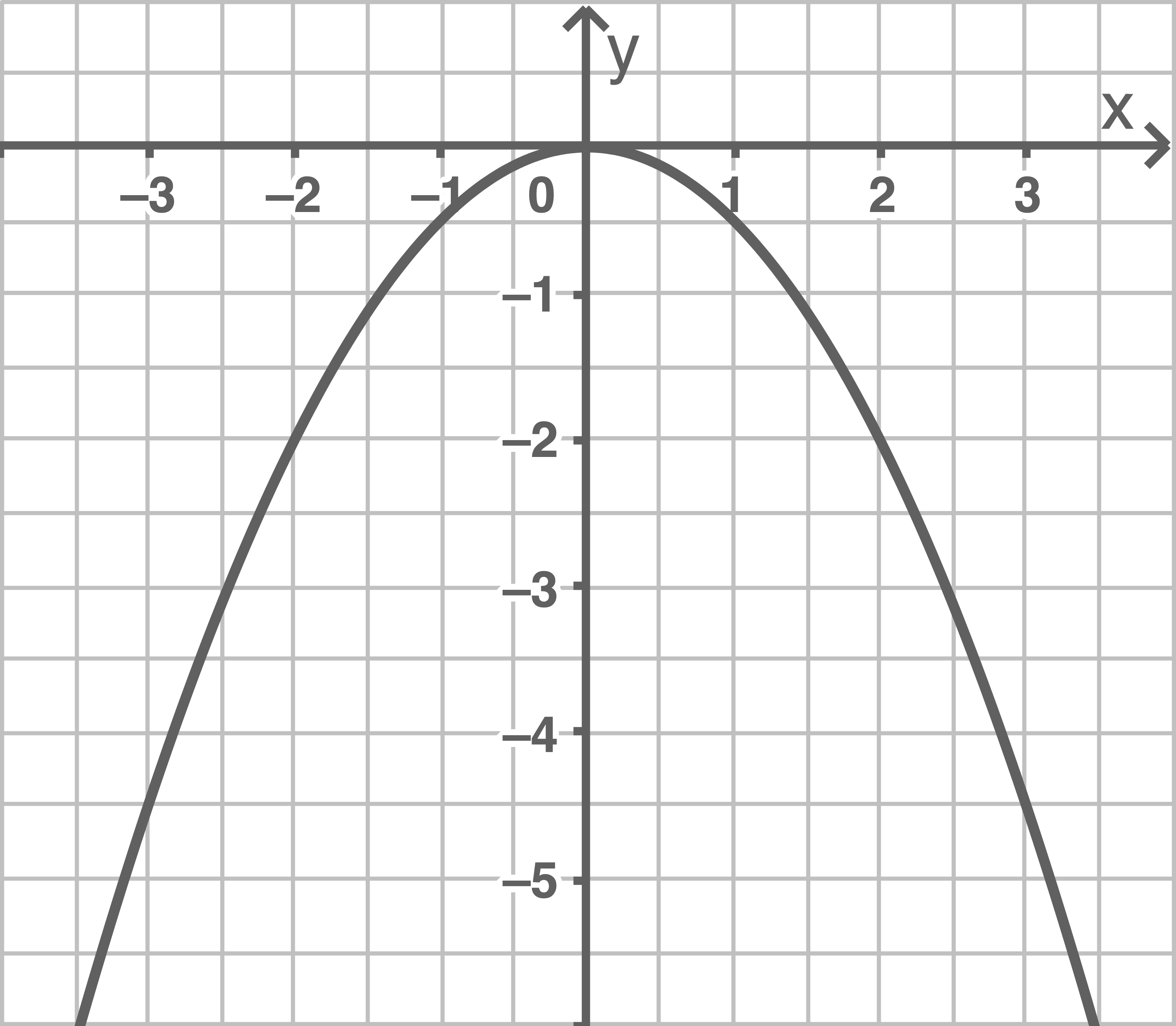
c)
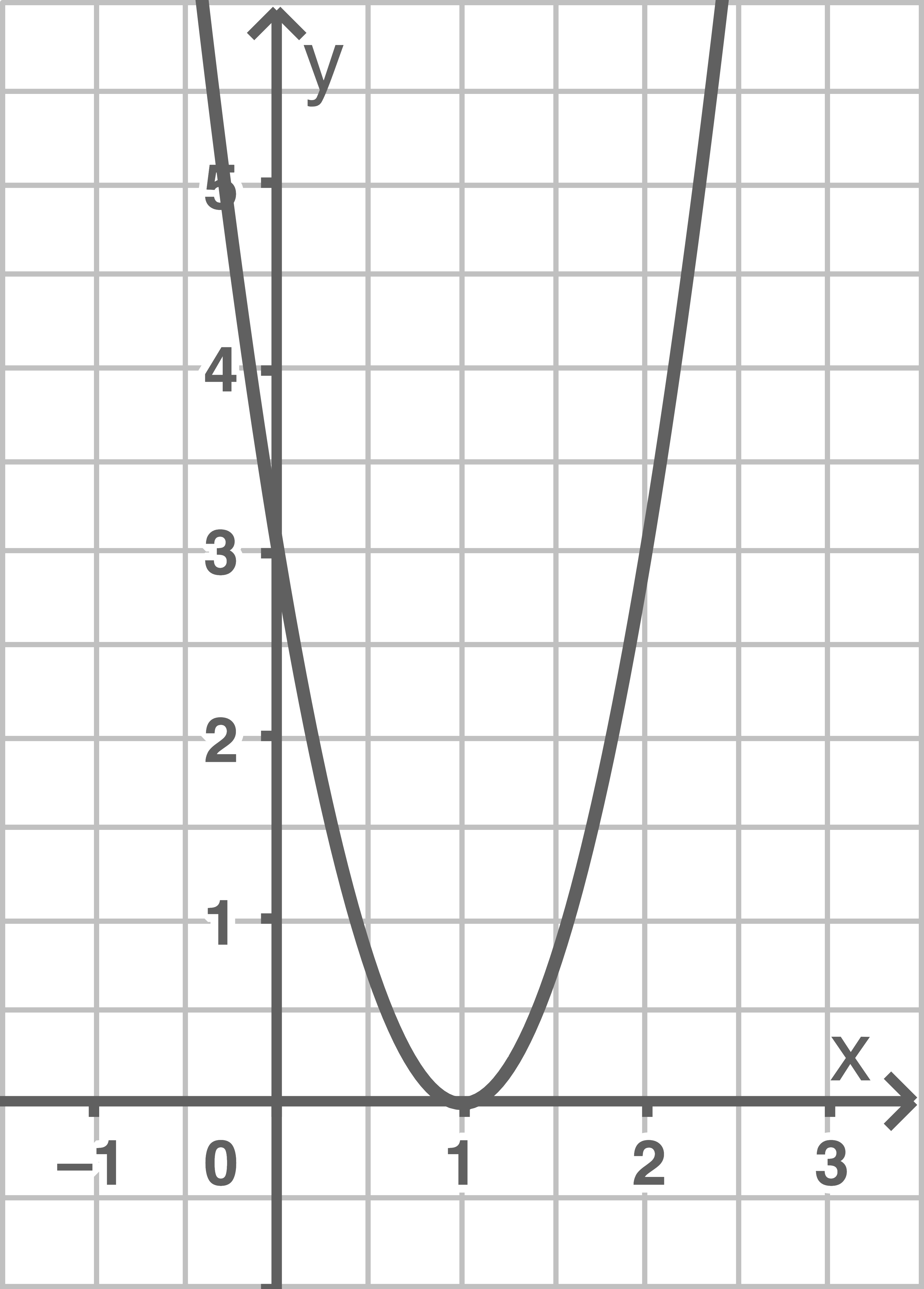
d)
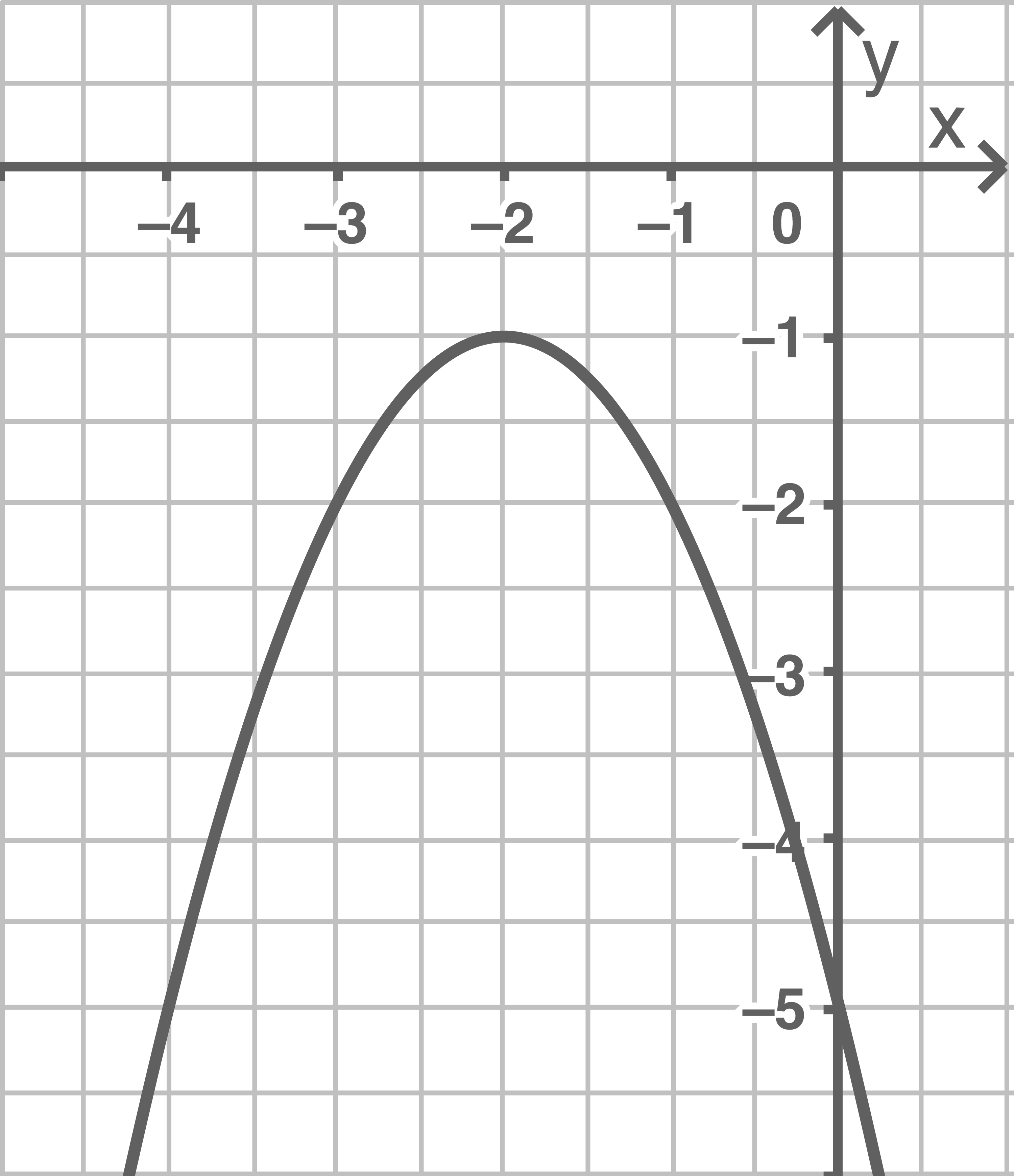
2
a)
Scheitelpunktform:
 allgemeine Form:
allgemeine Form:

b)
Scheitelpunktform:
 allgemeine Form:
allgemeine Form:
![\(\begin{array}[t]{rll}
f(x)&=& -(x+2)^2 \\[5pt]
&=& -(x^2+4x+4) \\[5pt]
&=& -x^2-4x-4
\end{array}\)](https://mathjax.schullv.de/c8143c323c7f88b08e79e7b27a2abb821255f10ba34697e93f101591d962fe26?color=5a5a5a)
c)
Scheitelpunktform:
 allgemeine Form:
allgemeine Form:
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{2}(x+1)^2-3 \\[5pt]
&=& \dfrac{1}{2}(x^2+2x+1)-3 \\[5pt]
&=& \dfrac{1}{2}x^2+x+\dfrac{1}{2}-3 \\[5pt]
&=& \dfrac{1}{2}x^2+x-\dfrac{5}{2}
\end{array}\)](https://mathjax.schullv.de/1b3be3f7c90fb0d97f868029ff86a6272c7acf39d0e57b7979e7490ac056772b?color=5a5a5a)
d)
Scheitelpunktform:
 allgemeine Form:
allgemeine Form:
![\(\begin{array}[t]{rll}
f(x)&=& -\dfrac{1}{3}(x-1)^2+2 \\[5pt]
&=& -\dfrac{1}{3}(x^2-2x+1)+2 \\[5pt]
&=& -\dfrac{1}{3}x^2+\dfrac{2}{3}x-\dfrac{1}{3}+2 \\[5pt]
&=& -\dfrac{1}{3}x^2+\dfrac{2}{3}x+\dfrac{5}{3}
\end{array}\)](https://mathjax.schullv.de/11895e4795f4928c90b17f6780efc0eff4863cb3b1fa92e251e1ace0e9e7356d?color=5a5a5a)