Potenzfunktionen mit negativem ganzzahligem Exponent
Der Graph einer Potenzfunktion  mit negativem ganzzahligem Exponenten
mit negativem ganzzahligem Exponenten  hat die folgenden Eigenschaften:
hat die folgenden Eigenschaften:
Der Graph verläuft durch den Punkt 
Falls  gerade ist, ist der Graph achsensymmetrisch zur
gerade ist, ist der Graph achsensymmetrisch zur  -Achse.
-Achse.
Falls  ungerade ist, ist der Graph punktsymmetrisch zum Ursprung.
ungerade ist, ist der Graph punktsymmetrisch zum Ursprung.
Achsensymmetrie
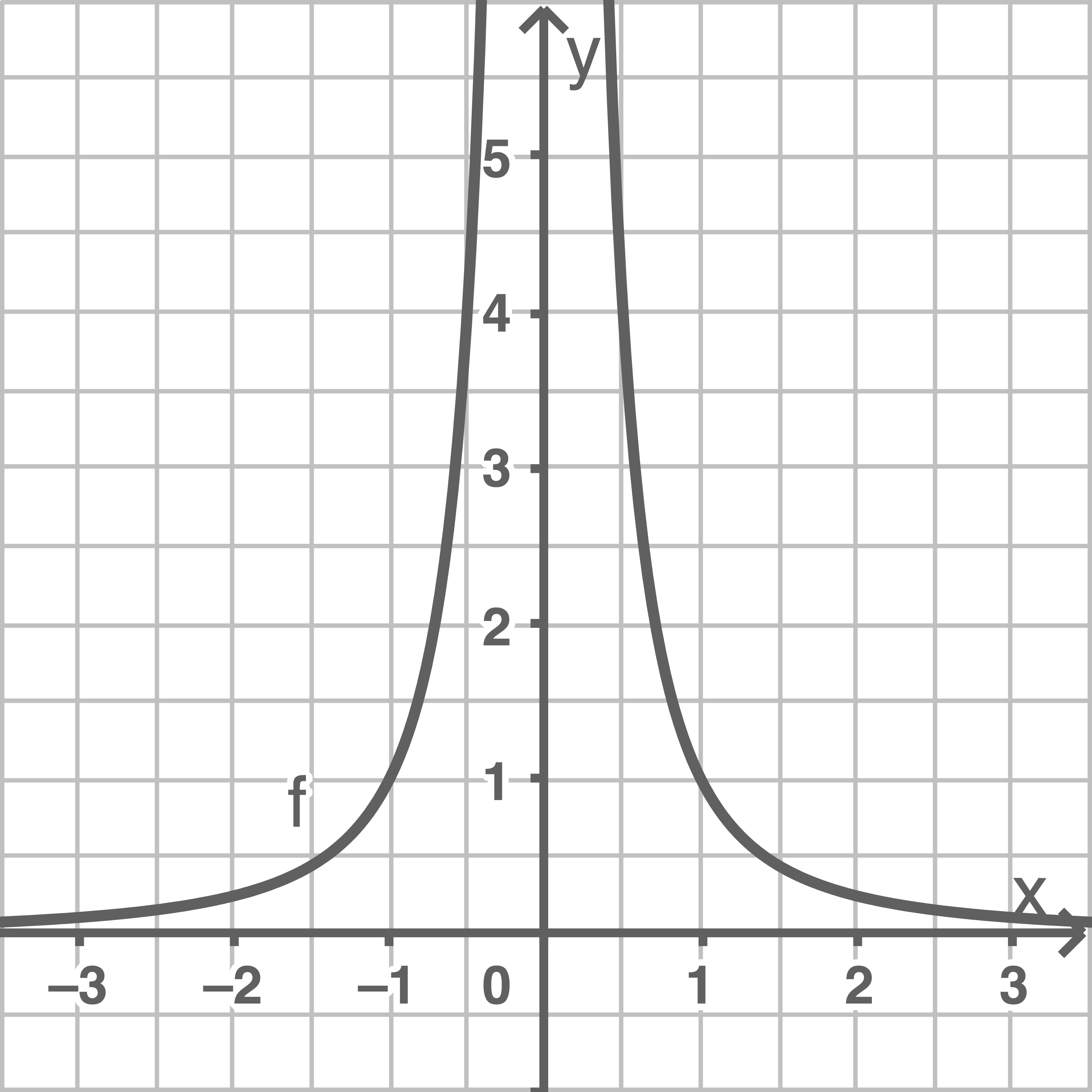

Potenzfunktion mit geradem Exponent, 
Punktsymmetrie
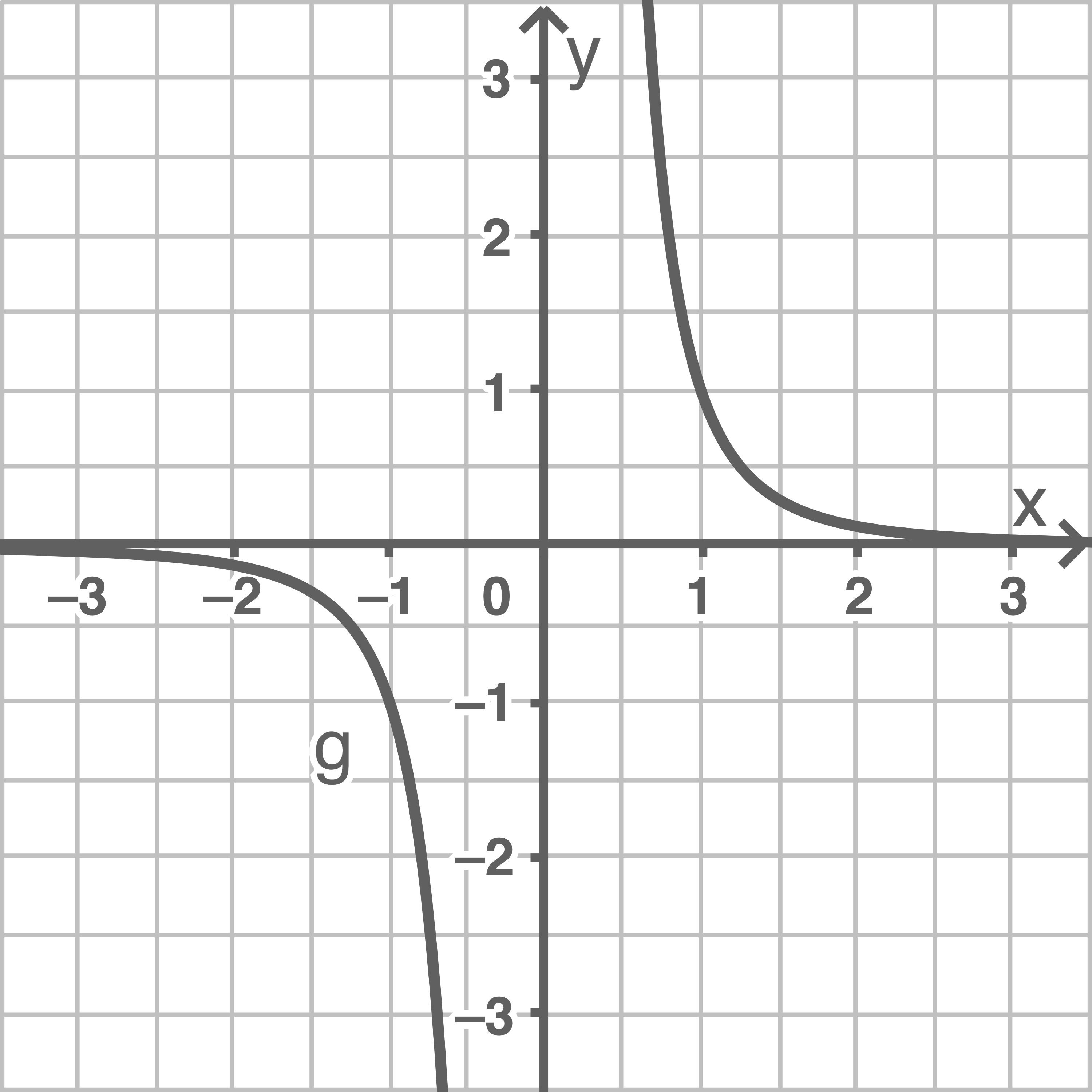

Potenzfunktion mit ungeradem Exponent, 
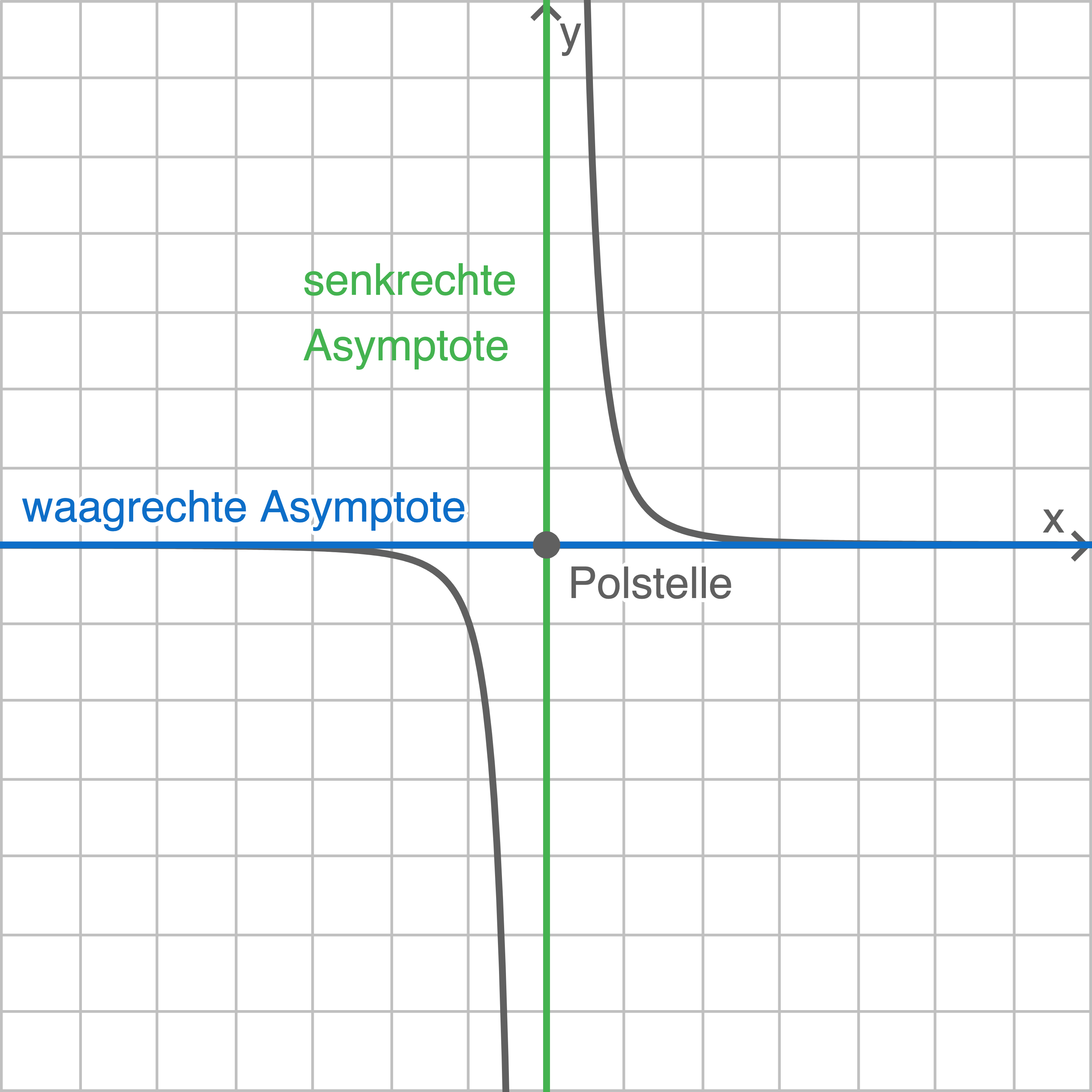
Asymptoten und Polstellen
Potenzfunktionen mit negativem ganzzahligem Exponent sind für  nicht definiert, sie haben dort eine Definitionslücke. Der Graph nähert sich immer weiter den Koordinatenachsen an, berührt sie jedoch nie.
Geraden, denen sich Graphen immer weiter nähern, ohne sie zu berühren, heißen Asymptoten.
Die Stelle, an der eine senkrechte Asymptote die
nicht definiert, sie haben dort eine Definitionslücke. Der Graph nähert sich immer weiter den Koordinatenachsen an, berührt sie jedoch nie.
Geraden, denen sich Graphen immer weiter nähern, ohne sie zu berühren, heißen Asymptoten.
Die Stelle, an der eine senkrechte Asymptote die  -Achse schneidet, heißt Polstelle.
-Achse schneidet, heißt Polstelle.

1
Gegeben ist die Funktion  mit
mit 
a)
Stelle eine Wertetabelle für den Bereich  in
in  Schritten auf.
Schritten auf.
b)
Zeichne den Graphen der Funktion mithilfe der Wertetabelle.
c)
Welche Symmetrie weist der Graph auf?
2
Fülle die Tabellen mithilfe der Symmetrieeigenschaften aus.
a)
b)
c)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
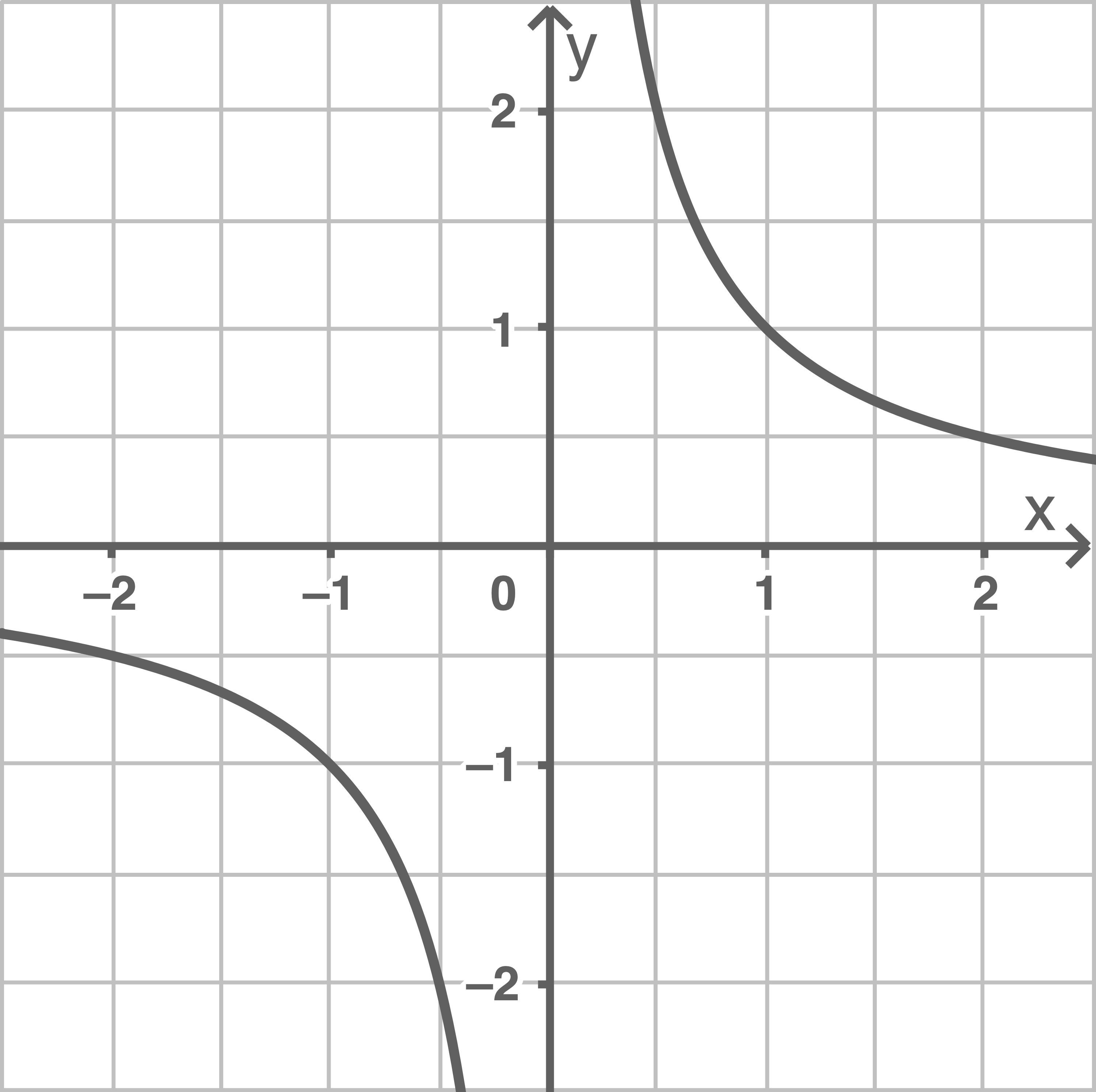
c)
Der Graph ist punktsymmetrisch zum Ursprung.
2
a)
b)
c)