Quadratische Funktionen
Eine Funktion  mit
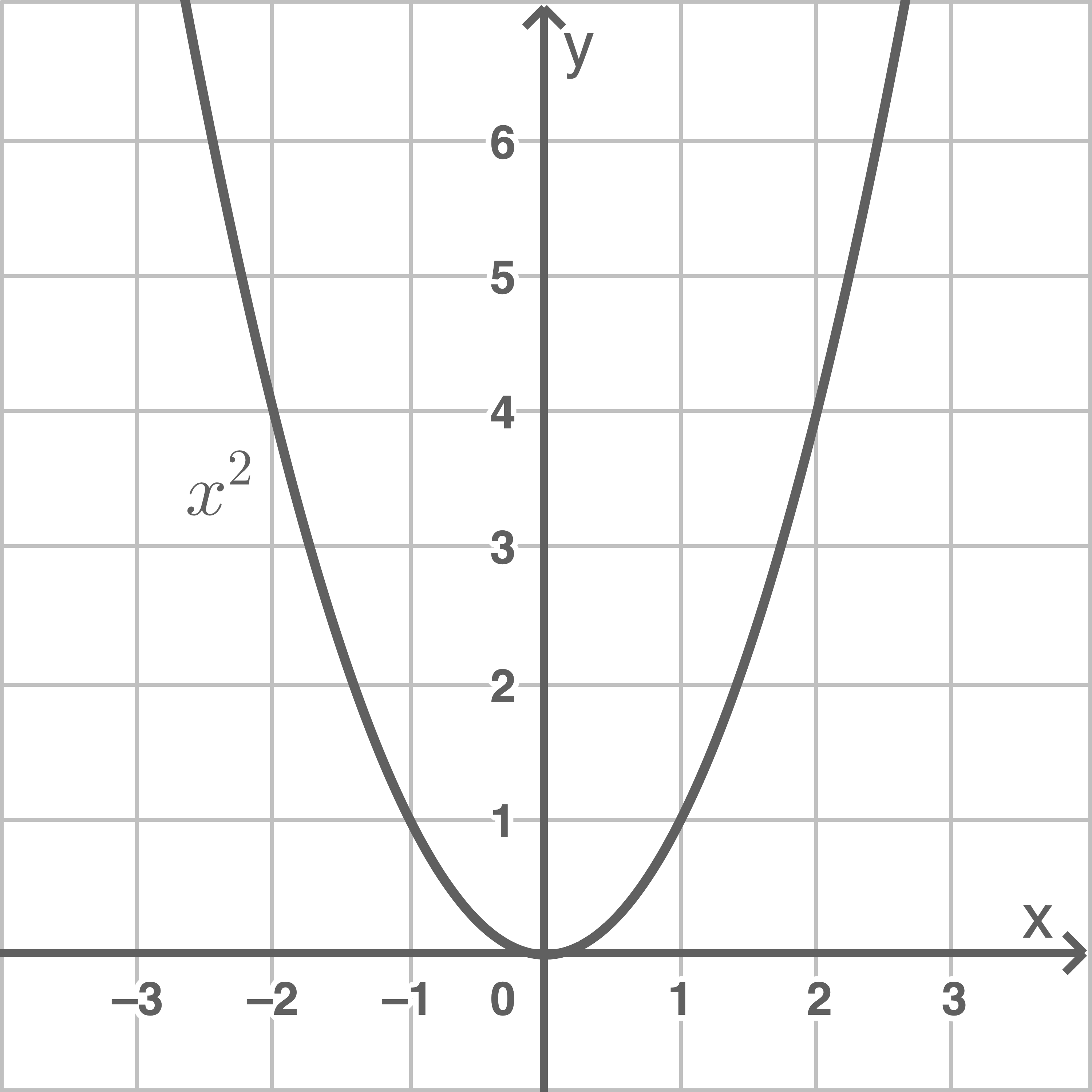
mit  heißt quadratische Funktion. Die Funktion
heißt quadratische Funktion. Die Funktion 
- ist monoton fallend für
- ist monoton steigend für
- hat den Definitionsbereich
- hat den Wertebereich
- hat den Tiefpunkt
im Koordinatenursprung. Dieser Punkt wird Scheitelpunkt genannt.
- ist symmetrisch zur
-Achse.
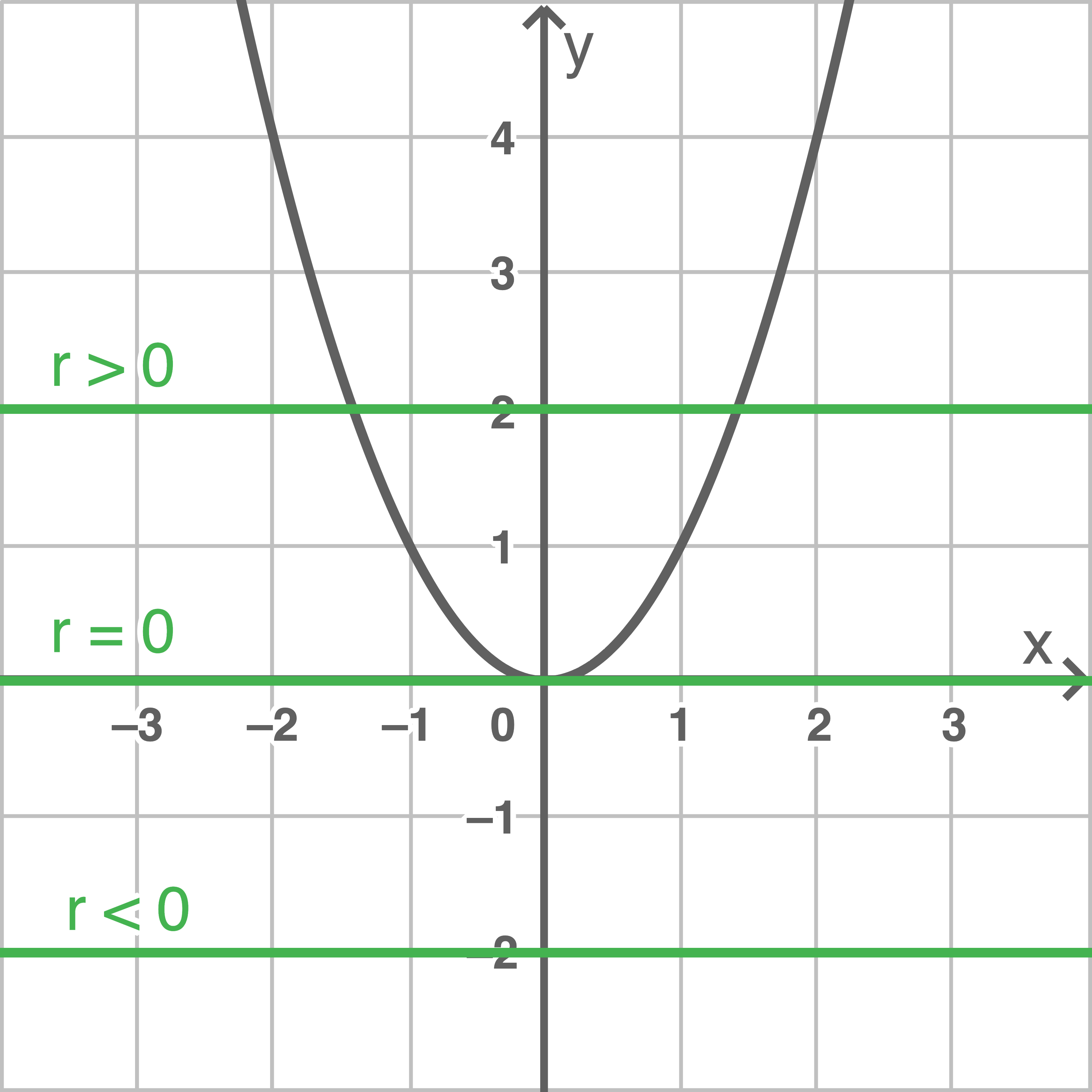
Eine Gleichung der Form  heißt quadratische Gleichung. Die Anzahl der Lösungen dieser Gleichung hängt vom Wert
heißt quadratische Gleichung. Die Anzahl der Lösungen dieser Gleichung hängt vom Wert  ab:
ab:
Die Gleichung hat die Lösungen
und
Die Gleichung hat die Lösung
Die Gleichung hat keine Lösung.
1
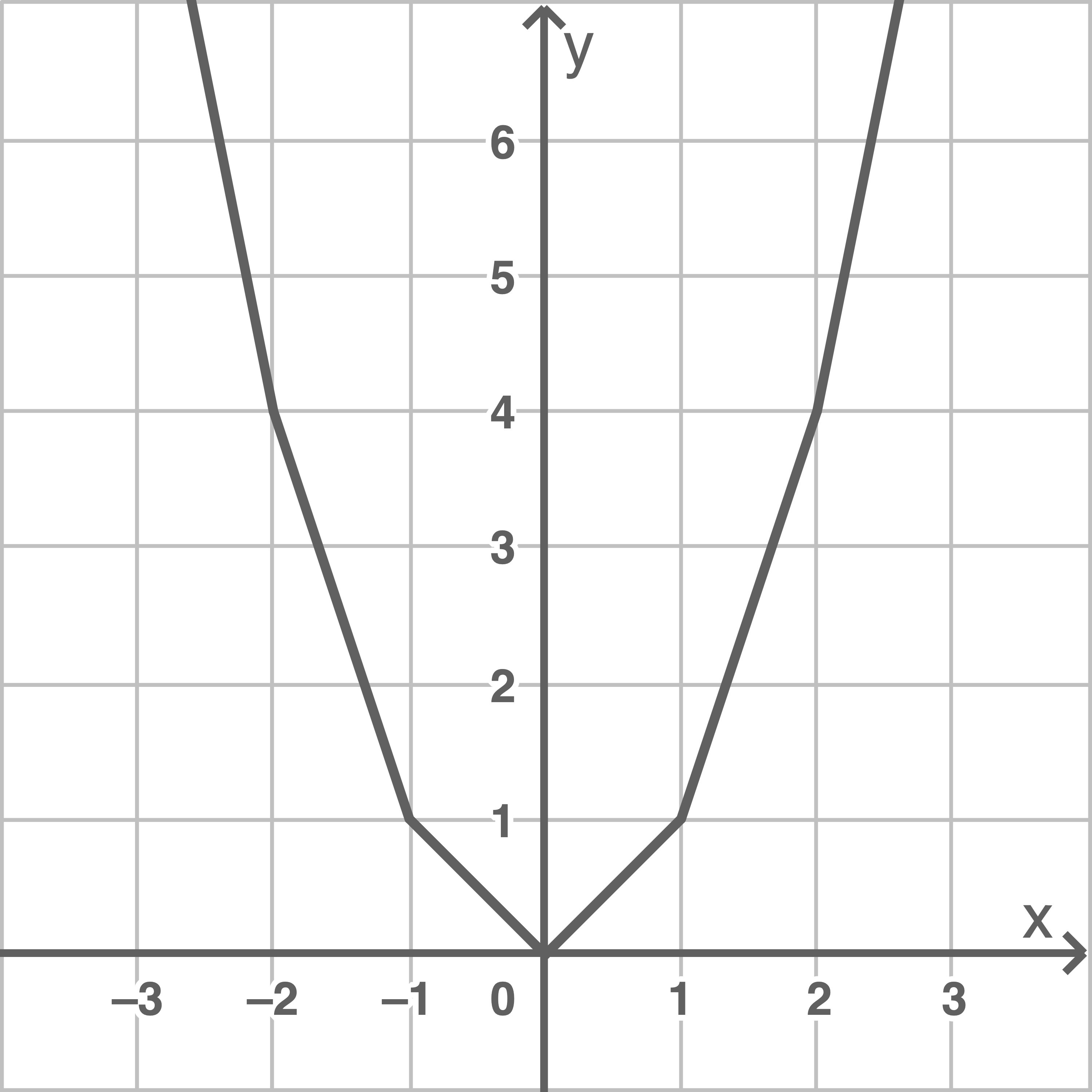
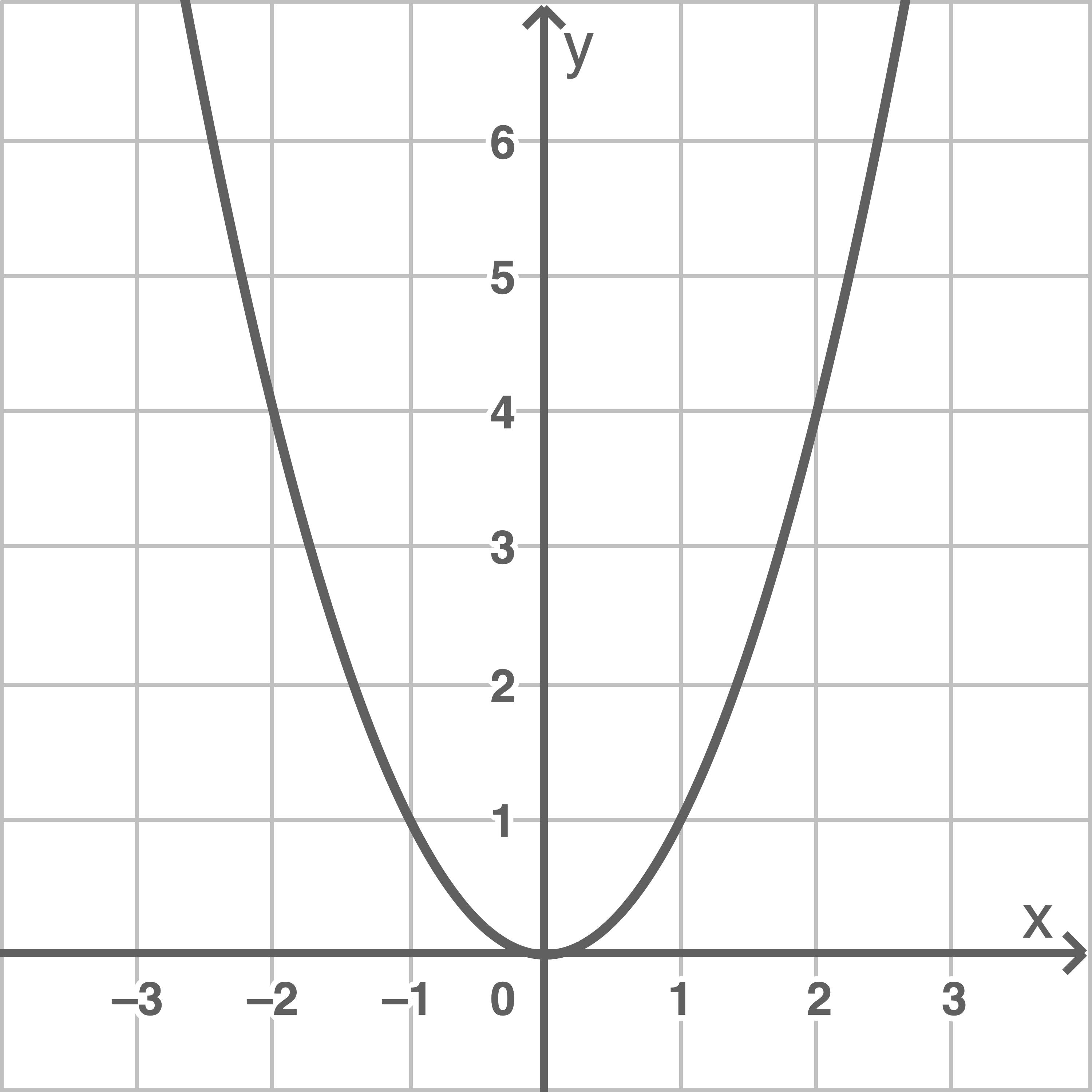
Erkläre, welcher Fehler beim Zeichnen der Normalparabel gemacht wurde und zeichne eine korrekte Normalparabel.

2
Gib an, wie viele Lösungen die quadratische Gleichung hat und berechne diese anschließend.




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Die Punkte auf der Normalparabel wurden mit geraden Strecken verbunden. Eine Parabel ähnelt jedoch eher einer Kurve, daher müssen die Verbindungsstrecken gekrümmt sein.

2
a)
Wegen  hat die quadratische Gleichung zwei Lösungen.
hat die quadratische Gleichung zwei Lösungen.
![\(\begin{array}[t]{rll}
x^2&=& 4 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
x_1&=& 2 \\
x_2&=& -2
\end{array}\)](https://mathjax.schullv.de/c780efc6cd66ded571b6edbf501dd43afb80300756a54ef72c7c7ee5b848cf76?color=5a5a5a)
b)
Wegen  hat die quadratische Gleichung keine Lösung.
hat die quadratische Gleichung keine Lösung.
c)
Wegen  hat die quadratische Gleichung zwei Lösungen.
hat die quadratische Gleichung zwei Lösungen.
![\(\begin{array}[t]{rll}
x^2&=& 2,25 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
x_1&=& 1,5 \\
x_2&=& -1,5
\end{array}\)](https://mathjax.schullv.de/8337b1ab0f0d5140a861a3dc0c9f0c9a522c65f4b53de280ad8951e28316c437?color=5a5a5a)
d)
Wegen  hat die quadratische Gleichung die Lösung
hat die quadratische Gleichung die Lösung 