Winkel zwischen Vektoren

Skalarprodukt zweier Vektoren

Für zwei parallele Vektoren $\overrightarrow{u}$ und $\overrightarrow{v}$ gilt:

Sind $\overrightarrow{u}$ und $\overrightarrow{v}$ gleichgerichtet, so gilt $\overrightarrow{u}*\overrightarrow{v}=|\overrightarrow{u}|\cdot |\overrightarrow{v}|.$
Sind $\overrightarrow{u}$ und $\overrightarrow{v}$ entgegengerichtet, so gilt $\overrightarrow{u}*\overrightarrow{v}=-|\overrightarrow{u}|\cdot |\overrightarrow{v}|.$

Für zwei beliebige Vektoren $\overrightarrow{u}\neq \overrightarrow{o}$ und $\overrightarrow{v}\neq \overrightarrow{o}$ mit eingeschlossenem Winkel $\alpha$ gilt:

$\overrightarrow{u}*\overrightarrow{v}=\cos(\alpha)\cdot |\overrightarrow{u}|\cdot |\overrightarrow{v}|$

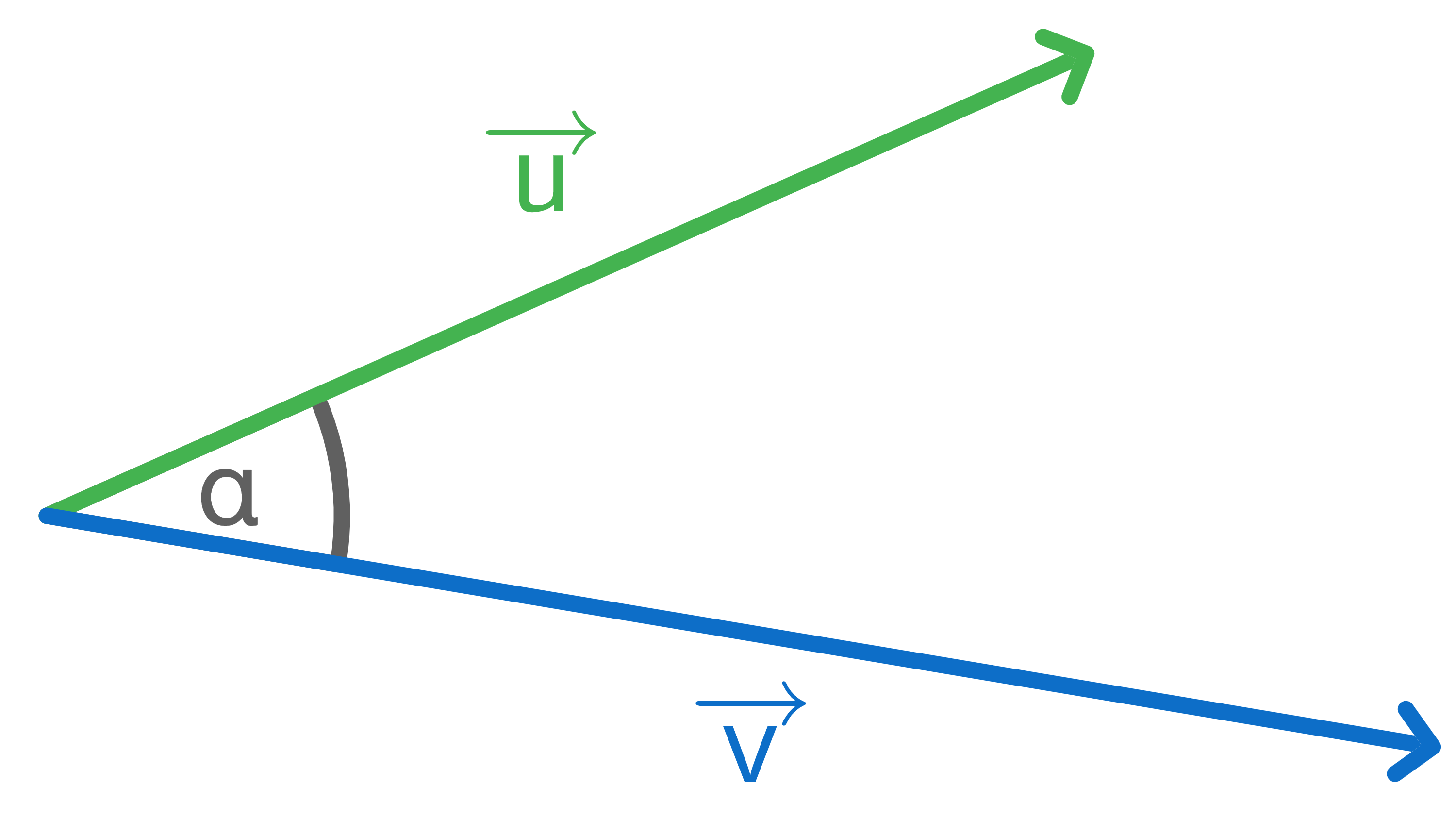
Winkel zwischen Vektoren im Raum

Für den Winkel $\alpha$ zwischen zwei Vektoren $\overrightarrow{u}\neq \overrightarrow{o}$ und $\overrightarrow{v}\neq \overrightarrow{o}$ gilt:

$\cos(\alpha)=\dfrac{\overrightarrow{u}*\overrightarrow{v}}{|\overrightarrow{u}|\cdot |\overrightarrow{v}|}$ mit $0°\leq \alpha \leq 180°$