Fälle beim rechnerischen Lösen von LGS
Beim Lösen von LGS können die folgenden drei Fälle auftreten. Das lineare Gleichungssystem hat
-
genau eine Lösung:
Beim Umformen des LGS ergibt sich eine eindeutige Lösung. Die zu den Gleichungen gehörenden Geraden haben genau einen gemeinsamen Schnittpunkt.
-
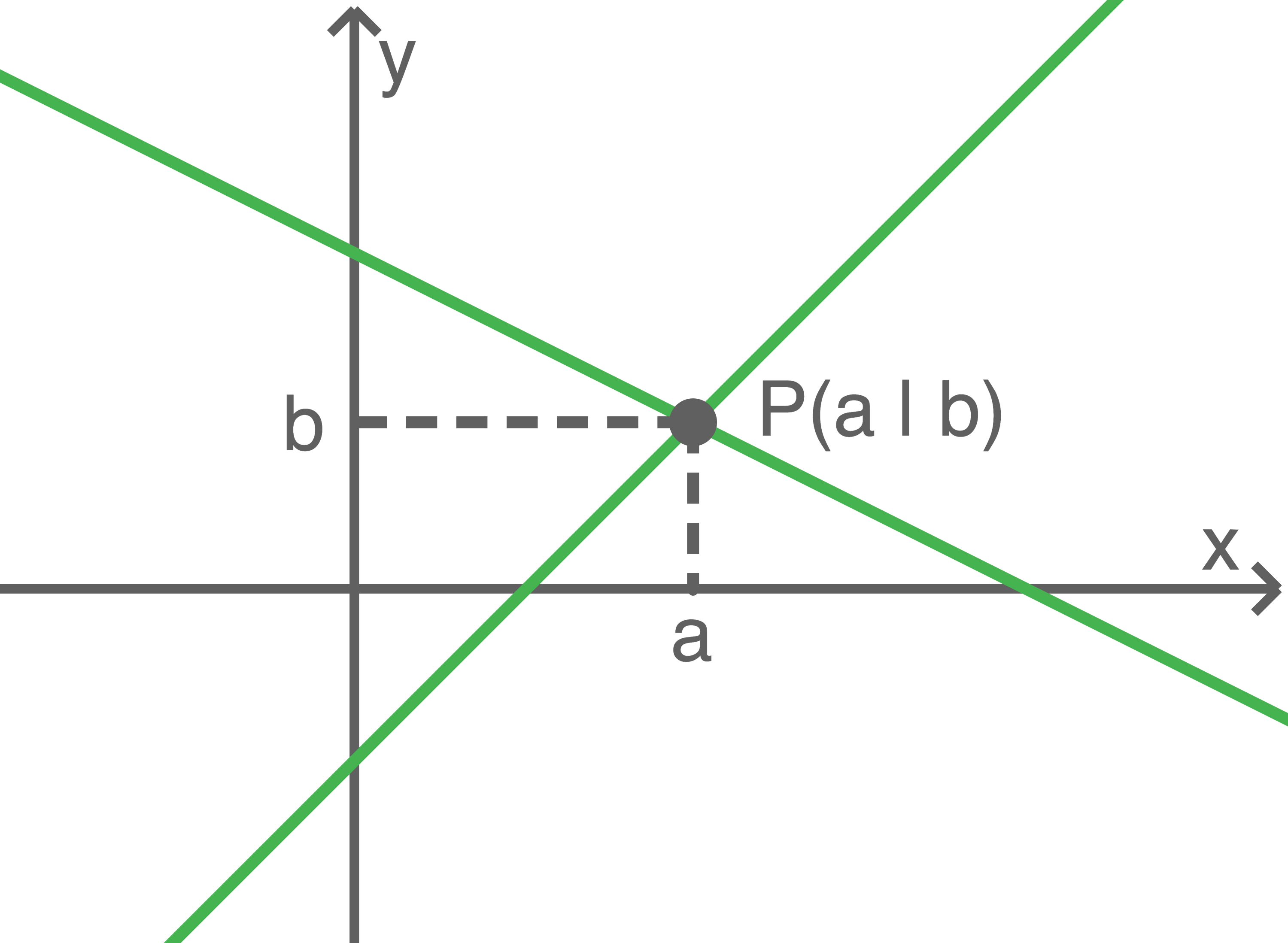
keine Lösung:
Beim Umformen des LGS ensteht eine falsche Aussage wie beispielsweise
Die zu den Gleichungen gehörenden Geraden verlaufen parallel und haben folglich keinen gemeinsamen Punkt.
-
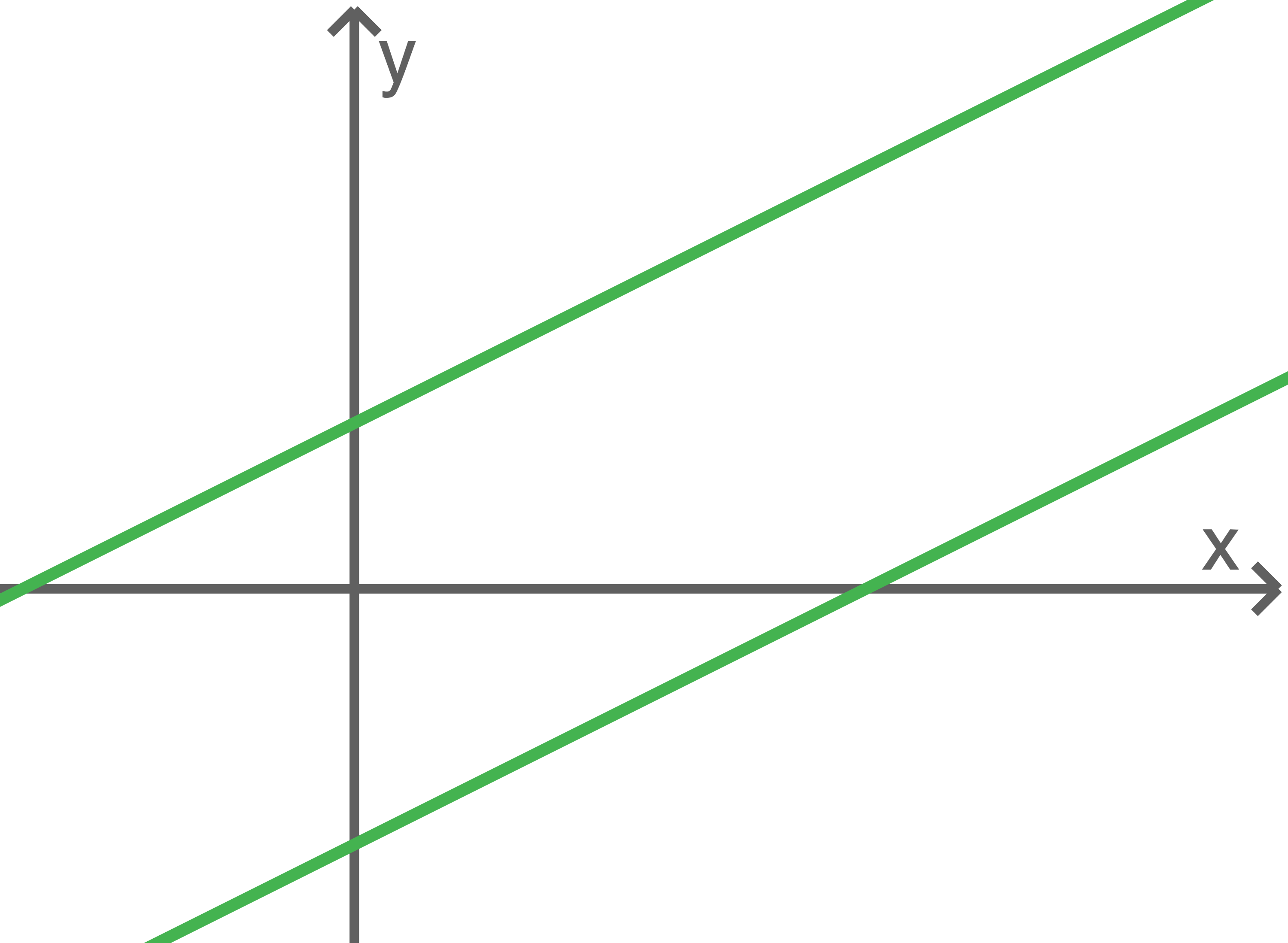
unendlich viele Lösungen:
Beim Umformen des LGS entsteht eine wahre Aussage wie beispielsweise
Die zu den Gleichungen gehörenden Geraden sind identisch und haben folglich alle Punkte gemeinsam.
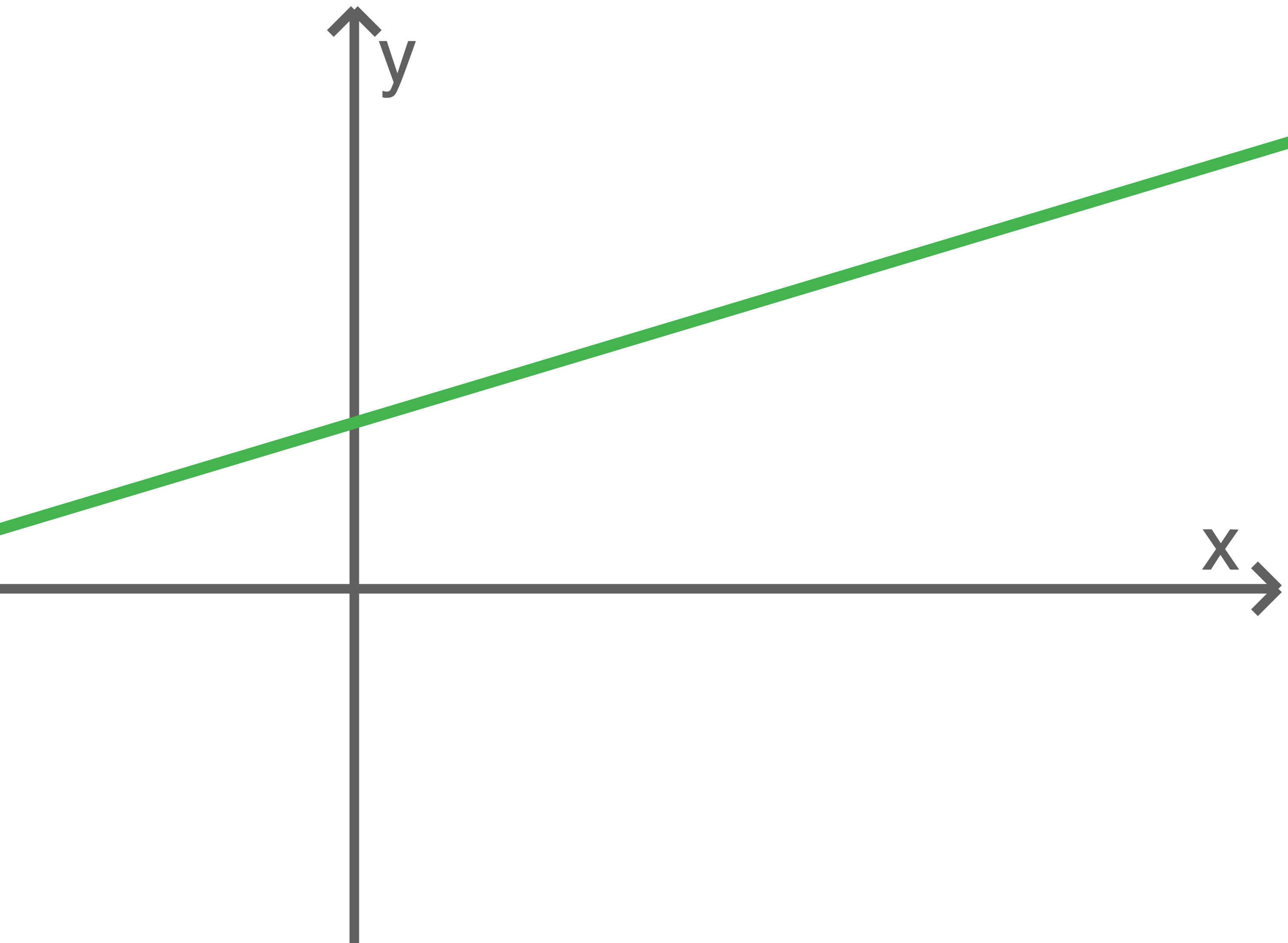
1
Bestimme rechnerisch mit einem geeigneten Verfahren, ob das LGS keine, eine oder unendlich viele Lösungen hat. Die Lösungsmenge muss nicht angegeben werden.
a)
b)
c)
2
Bestimme die Lösungsmenge des Gleichungssystems rechnerisch mit einem geeigneten Verfahren.
a)
b)
c)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
2
a)
Mit dem Additionsverfahren folgt:
![\(\begin{array}[t]{l}
\begin{array}{|llrrr|}
& -x+2y&=& -1 &\\
& 2x-4y&=& 3 &\\
\end{array}
&
\begin{array}{l}
\mid\;\cdot 2\\
\\
\end{array}
\end{array}
\)](https://mathjax.schullv.de/3a16d5a9e74a5a043bc4902cc1e6dd25baa12ce01837745cc43c8fcf843d4827?color=5a5a5a)
Addieren der beiden Gleichungen:
Das LGS hat keine Lösung:
b)
c)