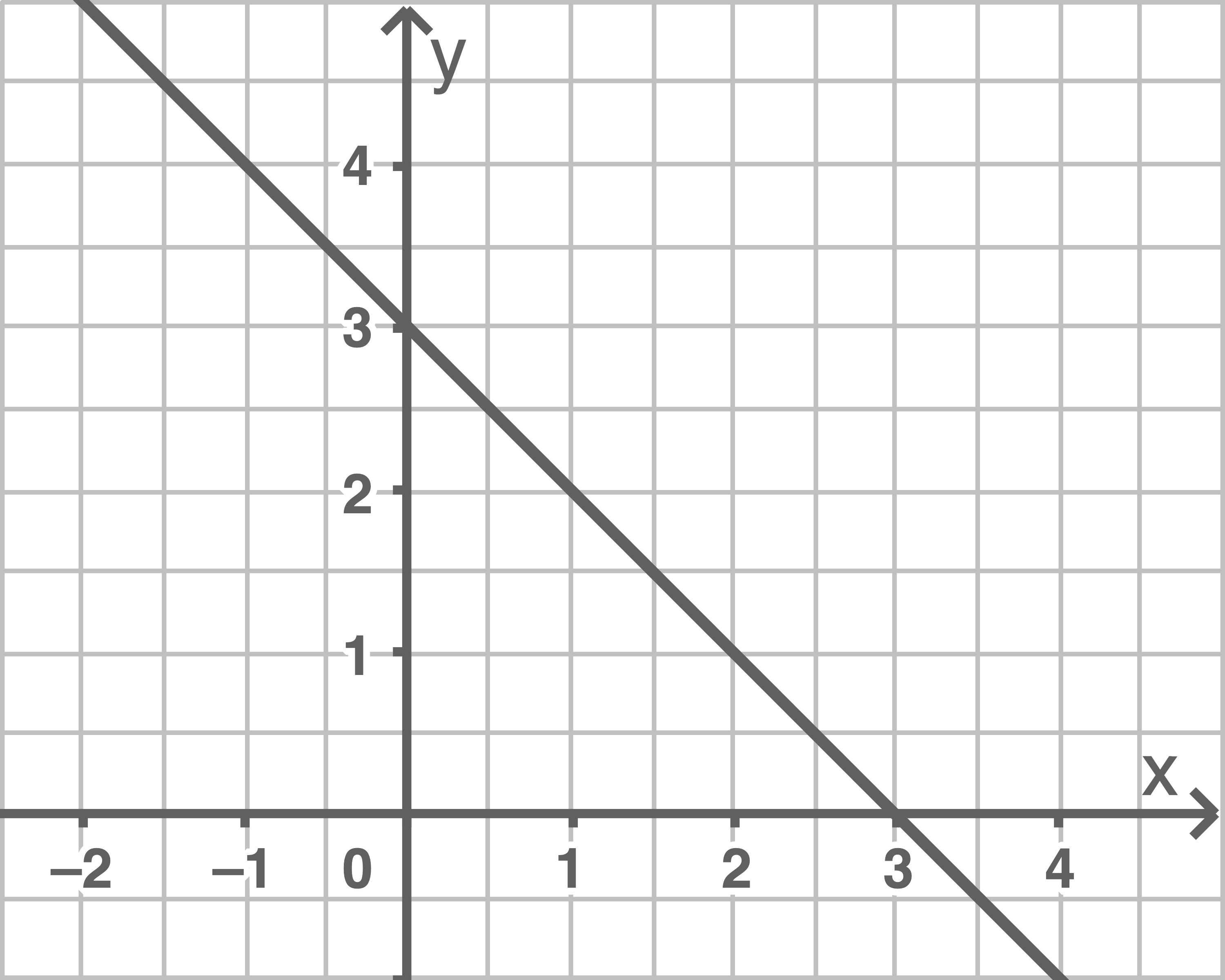
Lineare Gleichungen
Eine lineare Gleichung mit zwei Variablen ist eine Gleichung der Form  und jede Gleichung, die durch Äquivalenzumformungen auf diese Form gebracht werden kann.
Die Lösung einer solchen Gleichung ist durch ein Zahlenpaar
und jede Gleichung, die durch Äquivalenzumformungen auf diese Form gebracht werden kann.
Die Lösung einer solchen Gleichung ist durch ein Zahlenpaar  gegeben.
gegeben.

 Die Gleichung kann durch Umformungen in die Form
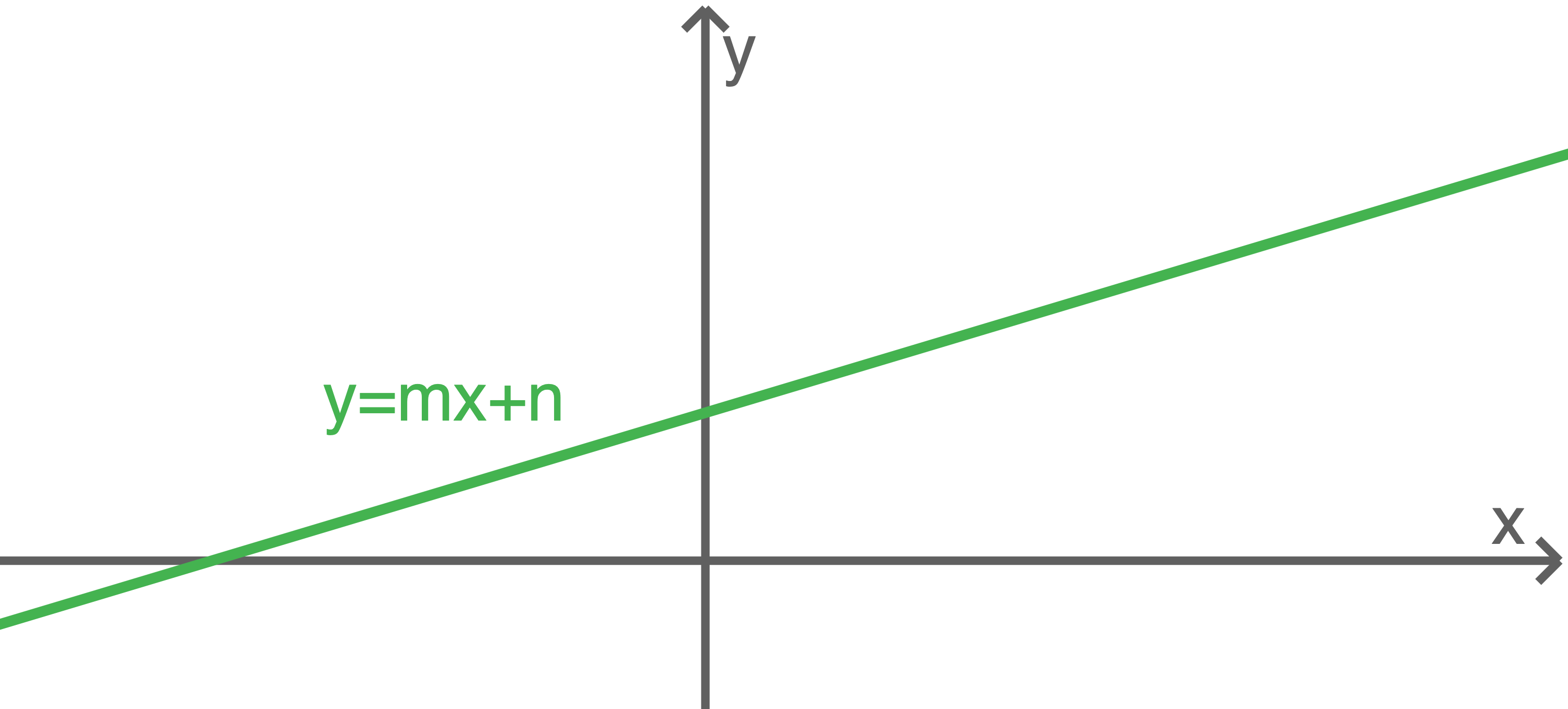
Die Gleichung kann durch Umformungen in die Form  gebracht werden. Dabei handelt es sich um eine Funktionsgleichung, deren Graph eine steigende, fallende oder zur
gebracht werden. Dabei handelt es sich um eine Funktionsgleichung, deren Graph eine steigende, fallende oder zur  -Achse parallele Gerade ist.
-Achse parallele Gerade ist.
 Die Gleichung kann durch Umformungen in die Form
Die Gleichung kann durch Umformungen in die Form  gebracht werden. Diese Gleichung ist keine Funktionsgleichung und ihr Graph ist eine zur
gebracht werden. Diese Gleichung ist keine Funktionsgleichung und ihr Graph ist eine zur  -Achse parallele Gerade.
-Achse parallele Gerade.
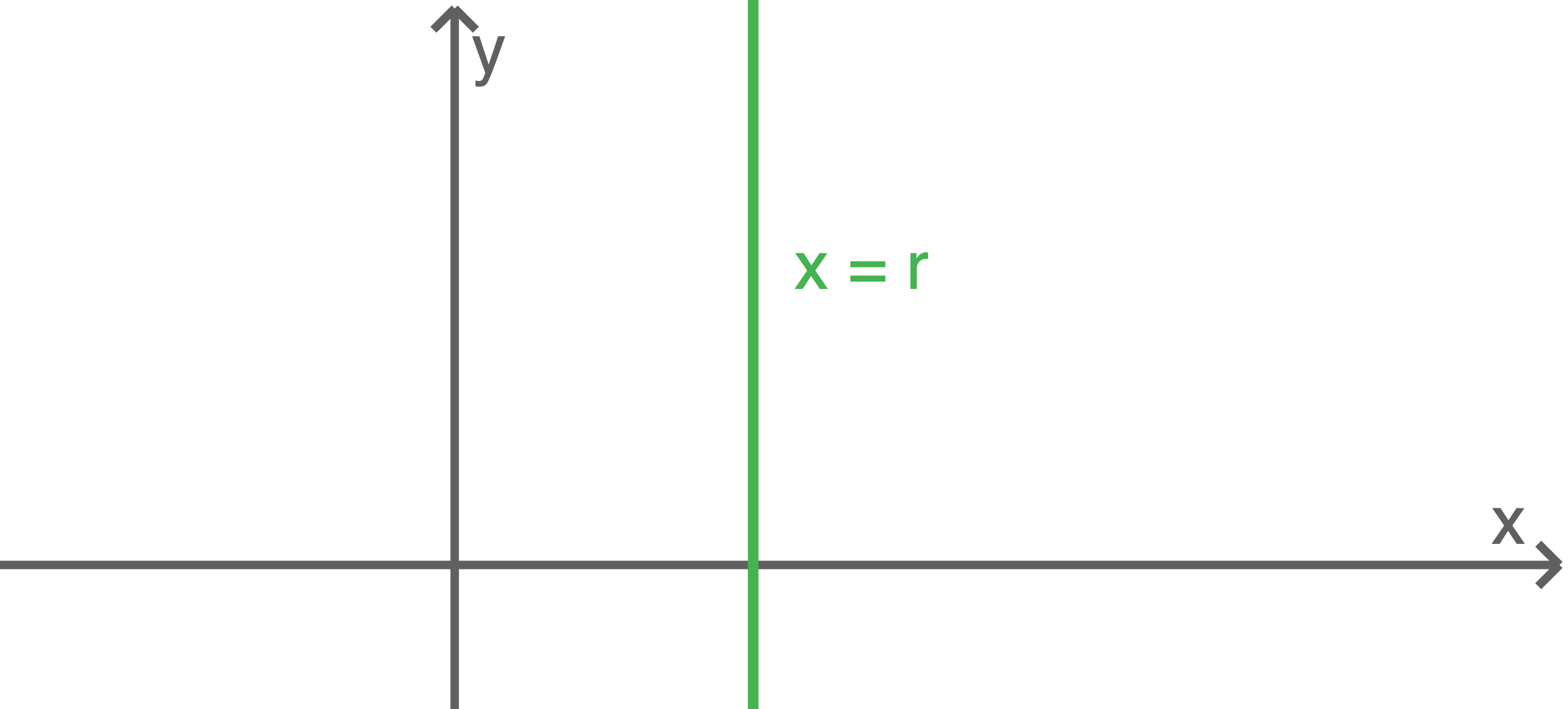
Darstellung linearer Gleichungen durch Geraden
Gegeben ist eine Gleichung der Form
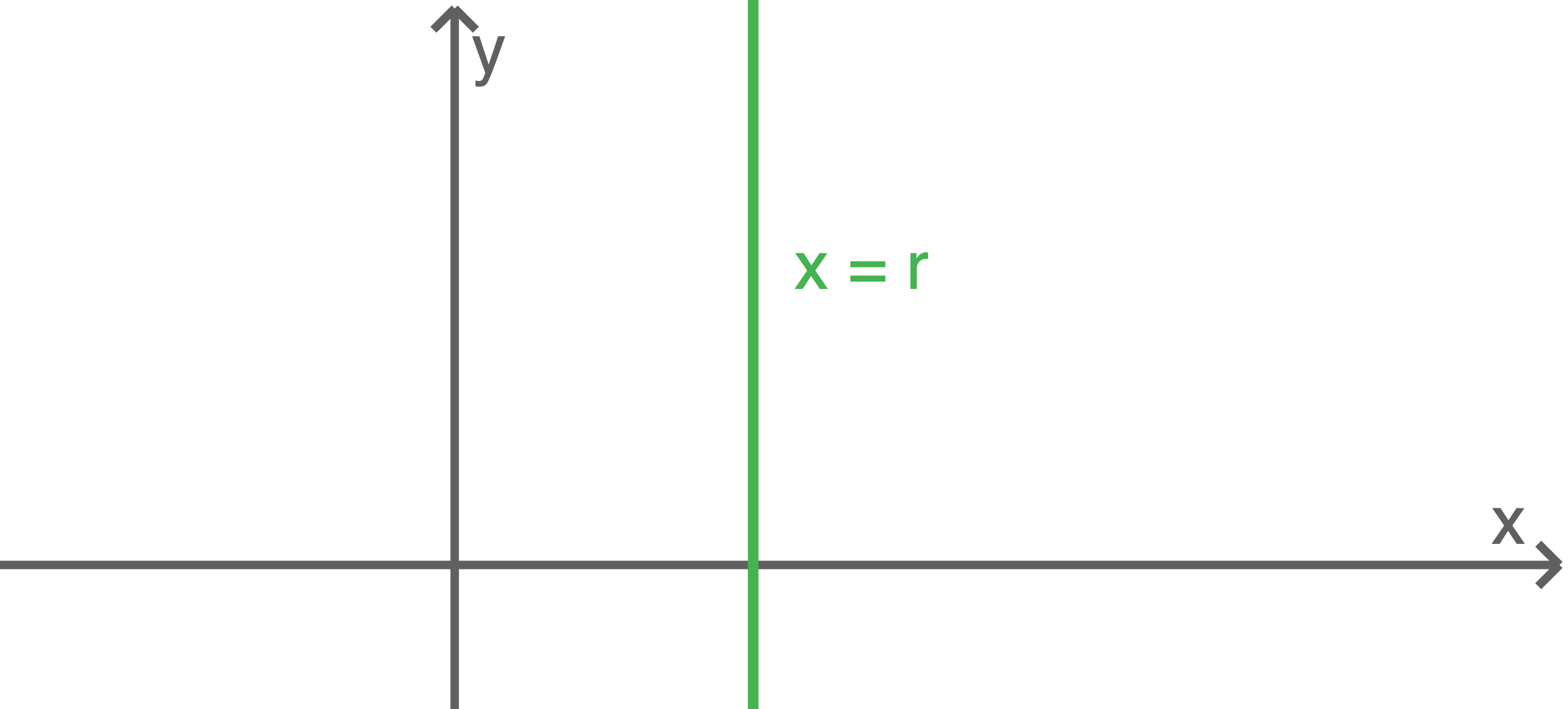
1
Welche der Punkte 


 und
und  liegen auf dem Graphen der linearen Gleichung
liegen auf dem Graphen der linearen Gleichung 
2
Ermittle die Funktionsgleichung durch Umstellen nach  und zeichne den zugehörigen Graphen.
und zeichne den zugehörigen Graphen.



a)
b)
c)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Punktprobe:
![\(\begin{array}[t]{rll}
P_1:\quad 3\cdot 2-2\cdot 1&=& 4 \\[5pt]
6-2&=& 4 \\[5pt]
4&=& 4
\end{array}\)](https://mathjax.schullv.de/4ab25ec6b8fed31a6e8dc0256b4ac3acf1782179c3fb8428901ff7659ea00006?color=5a5a5a) Der Punkt
Der Punkt  liegt auf dem Graphen der linearen Gleichung.
liegt auf dem Graphen der linearen Gleichung.
![\(\begin{array}[t]{rll}
P_2:\quad 3\cdot 4-2\cdot 4&=& 4 \\[5pt]
12-8&=& 4 \\[5pt]
4&=& 4
\end{array}\)](https://mathjax.schullv.de/99f63ac6bc72e48c15630fd619fc01f7cdacd7923599ee5beda752bb1ef94129?color=5a5a5a) Der Punkt
Der Punkt  liegt auf dem Graphen der linearen Gleichung.
liegt auf dem Graphen der linearen Gleichung.
![\(\begin{array}[t]{rll}
P_3:\quad 3\cdot 3-2\cdot 2&=& 4 \\[5pt]
9-4&=& 4 \\[5pt]
5&\neq& 4
\end{array}\)](https://mathjax.schullv.de/a8e83e2c3174fcb3a77f2d234e70b9caac899d859369bb4be57cc23b93de6659?color=5a5a5a) Der Punkt
Der Punkt  liegt nicht auf dem Graphen der linearen Gleichung.
liegt nicht auf dem Graphen der linearen Gleichung.
![\(\begin{array}[t]{rll}
P_4:\quad 3\cdot (-1)-2\cdot (-2)&=& 4 \\[5pt]
-3+4&=& 4 \\[5pt]
1&\neq& 4
\end{array}\)](https://mathjax.schullv.de/7f4797f256daf4f6d284a8408d4f84de4c14fb6bbdf75c6f7b078efef5a3ae13?color=5a5a5a) Der Punkt
Der Punkt  liegt nicht auf dem Graphen der linearen Gleichung.
liegt nicht auf dem Graphen der linearen Gleichung.
![\(\begin{array}[t]{rll}
P_5:\quad 3\cdot 0-2\cdot (-2)&=& 4 \\[5pt]
0+4&=& 4 \\[5pt]
4&=& 4
\end{array}\)](https://mathjax.schullv.de/a0497b282bde9937cc15a3bf10439eb5a9eadcfb771949968ac5b9daffb2a08d?color=5a5a5a) Der Punkt
Der Punkt  liegt auf dem Graphen der linearen Gleichung.
liegt auf dem Graphen der linearen Gleichung.
2
a)
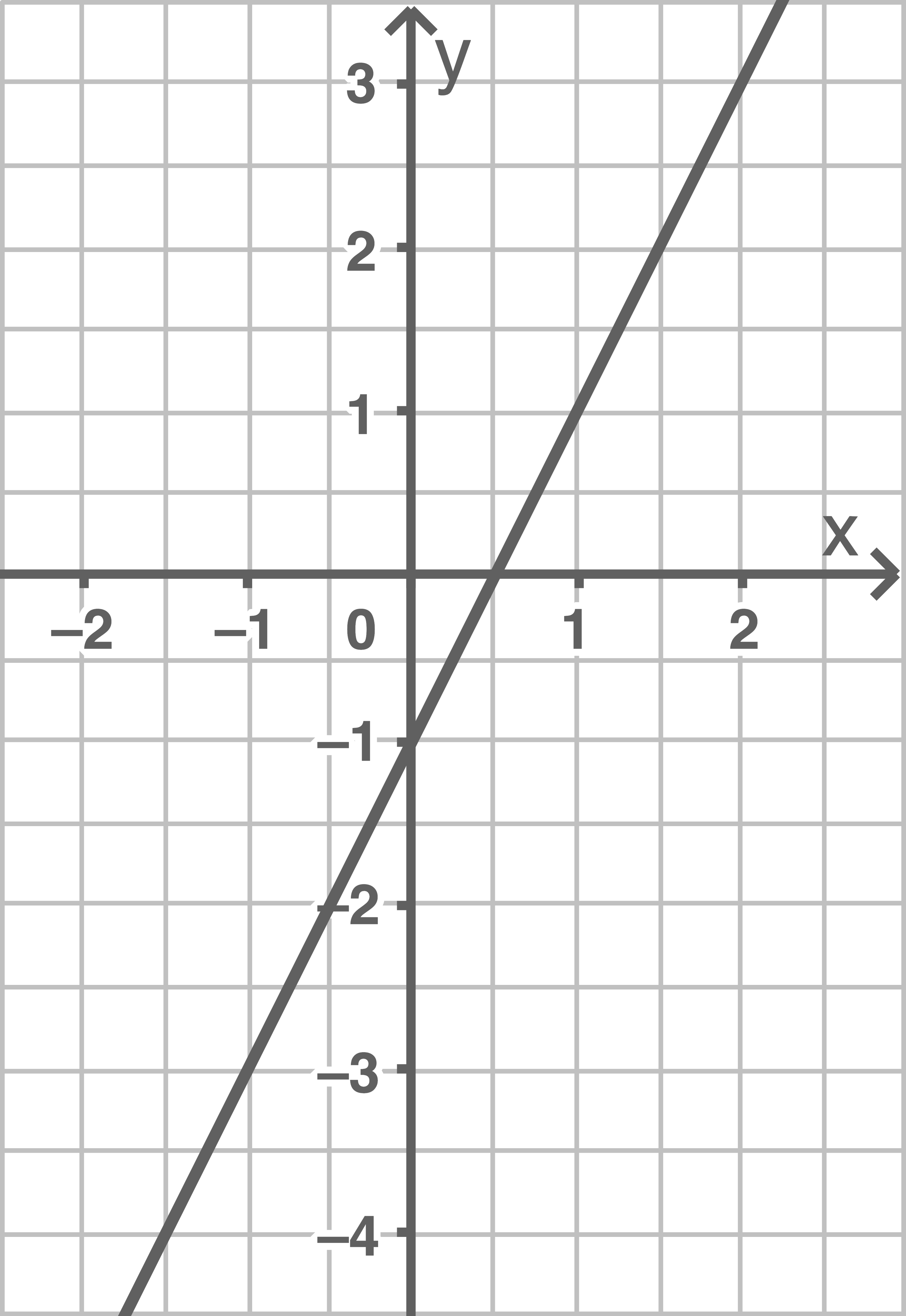
b)
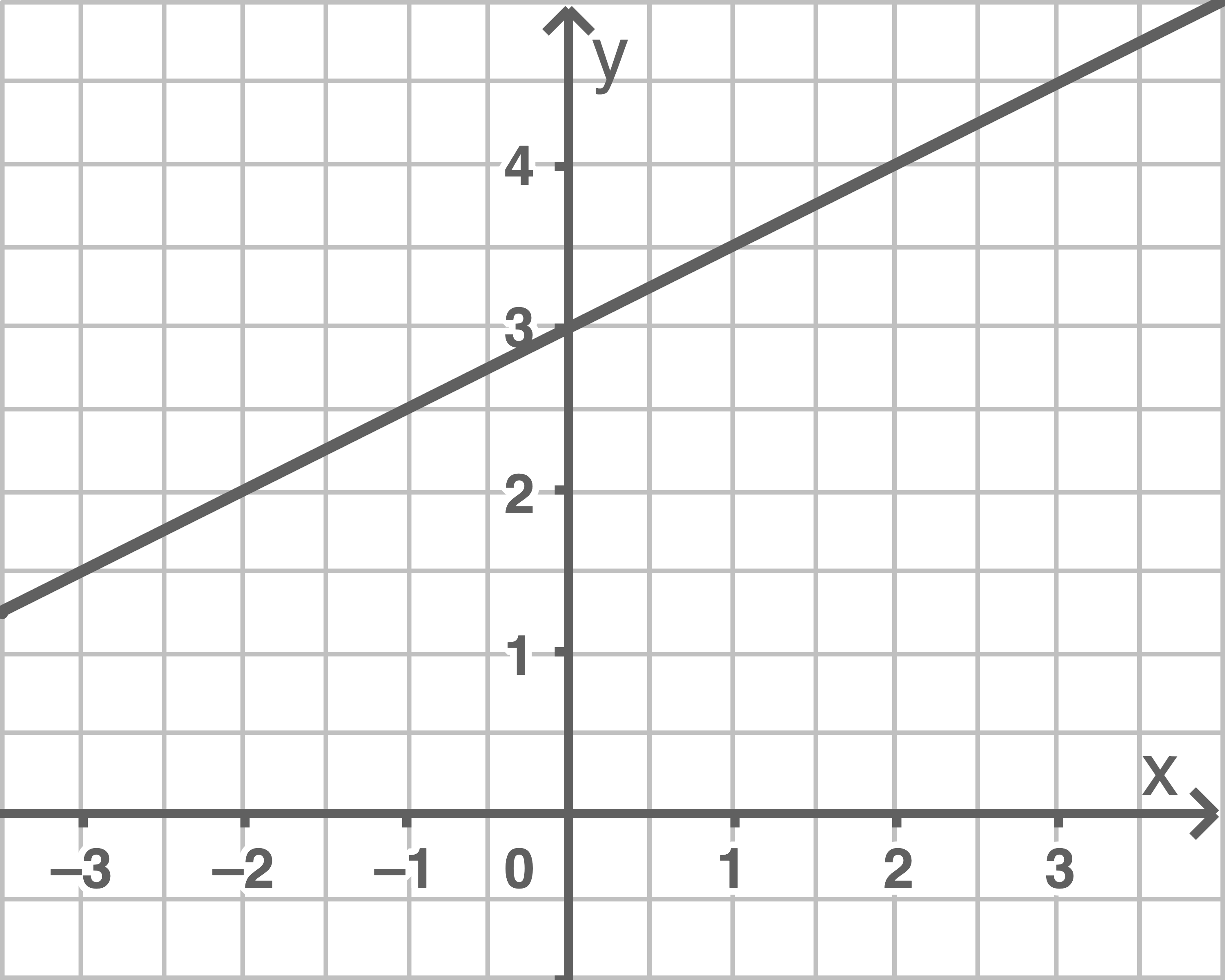
c)