Aufgabe 1 – Ammoniak

Ammoniak $(NH_3)$ ist eines der wichtigsten Industriegase. Es wird unter anderem als Ausgangsstoff für die Herstellung von Düngern, Medikamenten, Sprengstoffen, Farben, Lacken und Kunststoffen verwendet.

1.1

Beim HABER-BOSCH-Verfahren wird Ammoniak aus Wasserstoff und Stickstoff in einer Gleichgewichtsreaktion synthetisiert.

Stelle die Reaktionsgleichung der Ammoniaksynthese auf.
Begründe anhand der Reaktionsenthalpie, ob es sich bei der Ammoniaksynthese um eine exotherme oder eine endotherme Reaktion handelt.
Leite aus Tabelle 1 die Bedingungen für eine hohe Ammoniakausbeute ab. Begründe diese anhand des Prinzips von LE CHATELIER.

Tabelle anzeigen

	$1\,\text{bar}$	$30\,\text{bar}$	$100\,\text{bar}$	$200\,\text{bar}$	$1000\,\text{bar}$
$200^{\circ} C$	$15,3$	$67,6$	$80,6$	$85,8$	$98,3$
$300^{\circ} C$	$2,18$	$31,8$	$52,1$	$62,8$	$92,6$
$400^{\circ} C$	$0,44$	$10,7$	$23,1$	$36,3$	$79,8$
$500^{\circ} C$	$0,129$	$3,62$	$10,4$	$17,6$	$57,5$
$600^{\circ} C$	$0,049$	$1,43$	$4,47$	$8,25$	$31,4$
$700^{\circ} C$	$0,022$	$0,66$	$2,14$	$4,11$	$12,9$

(4 VP)

1.2

In einem Versuchsreaktor befinden sich vor Reaktionsbeginn $1 \,\text{mol}$ Stickstoff und $3 \,\text{mol}$ Wasserstoff. Bei einer Temperatur von $200^{\circ} C$ und einem Druck von $100\,\text{bar}$ liegen im Gleichgewicht $1,785 \,\text{mol}$ Ammoniak vor.

Berechne die Stoffmengen an Wasserstoff und Stickstoff im Gleichgewicht.
Zeige durch Berechnung, dass im Gleichgewicht $1,785 \,\text{mol}$ Ammoniak einem Stoffmengenanteil von $80,6 \,\%$ entsprechen.

(3 VP)

Die Verbrennungsenthalpie von Ammoniak soll experimentell bestimmt werden. Dazu wird Ammoniak in einem Verbrennungskalorimeter für Gase verbrannt (Abb. 1). In diesem werden $1 000\,\text{g}$ Trichlormethan $($ spez. Wärmekapazität $c = 0,95 \,\text{J} \cdot \,\text{g}^{–1} \cdot \,\text{K}^{–1})$ als Kalorimeterflüssigkeit genutzt.

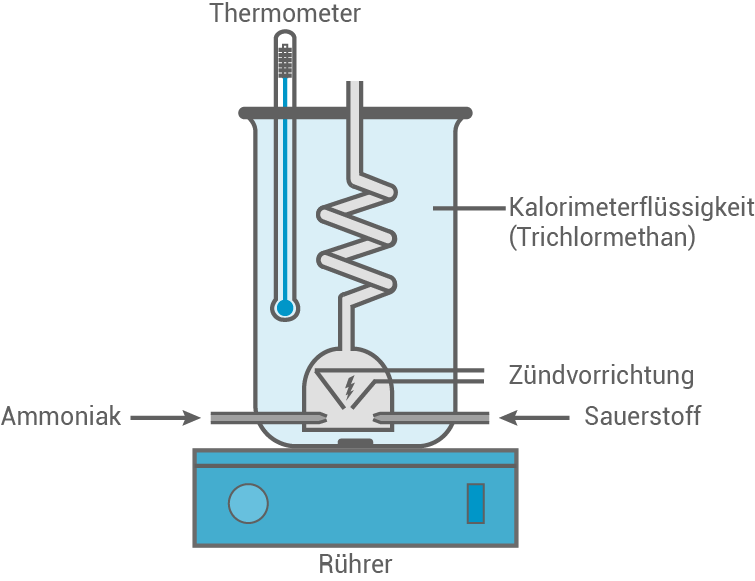
Abbildung 1: Verbrennungskalorimeter

2.1

In einem Experiment wird die Temperatur in Abhängigkeit von der Zeit gemessen. Nach Beginn der Messung wird eine Masse von $m = 0,4 \,\text{g}$ Ammoniak kontinuierlich mit Sauerstoff in das Reaktionsgefäß eingeleitet und verbrannt. Es wird folgender Temperaturverlauf aufgezeichnet:

Zeit in Minuten	Temperatur in $\color{#ffffff}{^\circ C}$
$0$	$25,0$
$0,5$	$25,1$
$1,0$	$25,0$
$1,5$	$25,0$
$2,0$	$25,5$
$2,5$	$26,4$
$3,0$	$27,0$
$3,5$	$27,8$
$4,0$	$28,5$
$4,5$	$29,3$

Zeit in Minuten	Temperatur in $\color{#ffffff}{^\circ C}$
$5,0$	$30,0$
$5,5$	$30,7$
$6,0$	$31,4$
$6,5$	$32,0$
$7,0$	$32,3$
$7,5$	$32,1$
$8,0$	$32,0$
$8,5$	$31,8$
$9,0$	$31,7$
$9,5$	$31,6$

Tabelle 2: Temperaturverlauf bei der Verbrennung des Ammoniaks

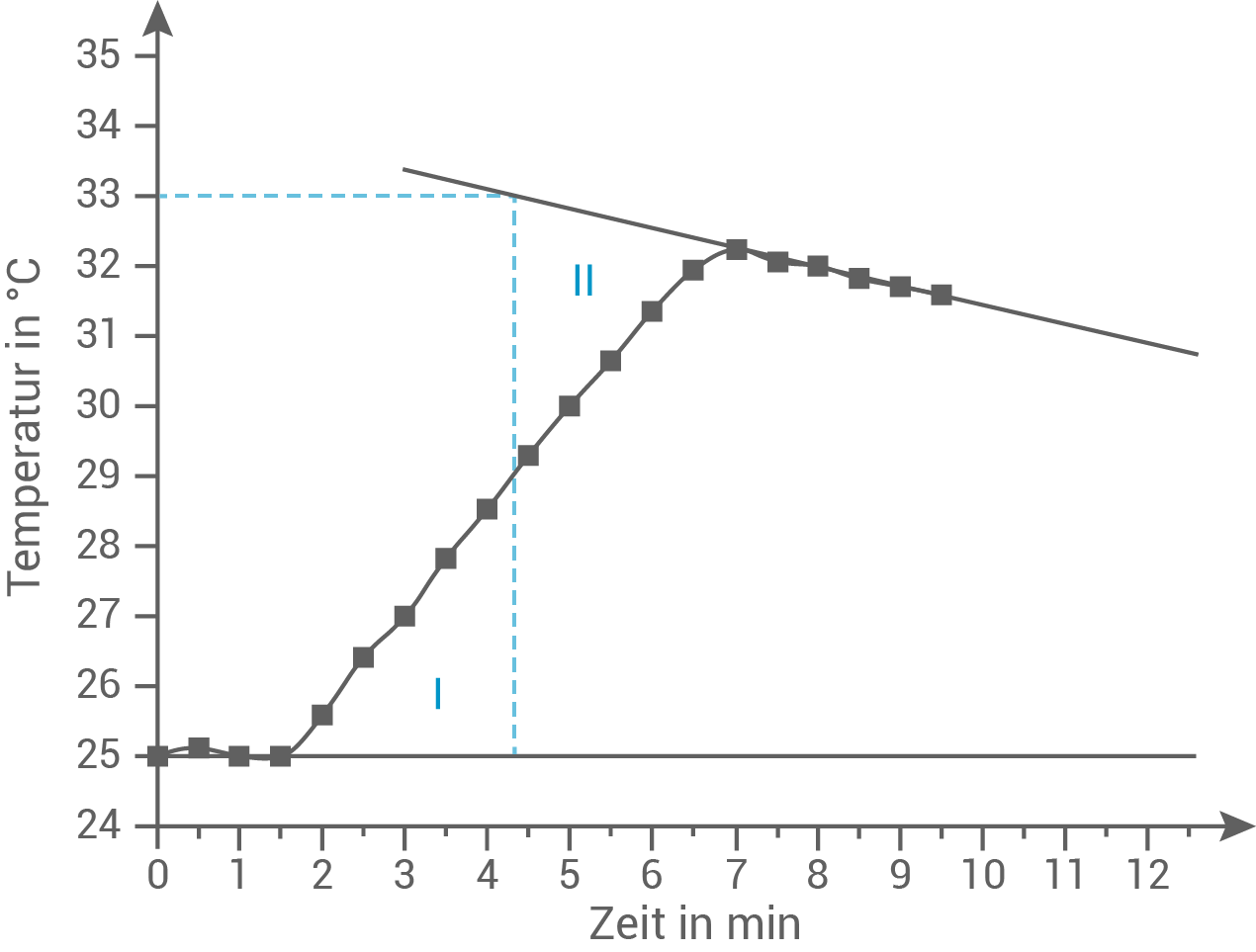
Stelle die Daten aus Tabelle 2 in einem Diagramm dar.
Ermittle anhand deiner Darstellung jeweils den Zeitpunkt, zu dem die Verbrennung von Ammoniak beginnt und zu dem sie endet.
Begründe die fallende Temperatur in den letzten Minuten der Messung.
Ermittle die vom Trichlormethan während der Verbrennung aufgenommene Wärmemenge $Q$ .

(7 VP)

2.2

In einem weiteren Experiment mit diesem Verbrennungskalorimeter wird bei der Verbrennung von $0,5 \,\text{g}$ Ammoniak eine Wärmemenge $Q = 9,5 \,\text{kJ}$ bestimmt. Das Ergebnis des Experiments soll anhand von Literaturwerten überprüft werden.

Berechne die Reaktionsenthalpie für die Verbrennung von $1 \,\text{mol}$ Ammoniak ausgehend von der experimentell bestimmten Wärmemenge $Q$ (Fall A).
Berechne die Reaktionsenthalpie für die Verbrennung von $1 \,\text{mol}$ Ammoniak unter Verwendung der thermodynamischen Daten aus Anlage 4 (Fall B).
Ammoniak reagiert bei der Verbrennung vereinfacht nach folgender Gleichung:

$4 \,NH_3\,_\text{(g)} + 3\, O_2 \,_\text{(g)}$ $\longrightarrow$ $2\,N_2 \,_\text{(g)} + 6\, H_2O \,_\text{(l)}$
Überprüfe qualitativ, ob die folgenden Aussagen die Abweichung zwischen Fall A und Fall B erklären können:

a)

Es wurden unwissentlich mehr als $1 000 \,\text{g}$ Trichlormethan in die Apparatur gegeben.

b)

Ein Teil des entstehenden Wassers ist nicht kondensiert.

(6 VP)

(20 VP)

1.1

Reaktionsgleichung der Ammoniaksynthese

$N_2\,_\text{(g)} + 3\,H_2\,_\text{(g)}$ $\rightleftharpoons$ $2\,NH_3\,_\text{(g)}$

Reaktionsenthalpie

Die Tabelle mit den thermodynamischen Daten zeigt für die Ammoniak-Bildung unter Standardbedingungen eine Reaktionsenthalpie von $\Delta_fH^0 = -46 \,\text{kJ} \cdot \,\text{mol}^{-1}.$

Das negative Vorzeichen zeigt, dass es sich um eine exotherme Reakton handelt.

Bedingungen für eine hohe Ammoniakausbeute

Da es sich um eine Gleichgewichtsreaktion handelt, gilt das Prinzip von LE CHATELIER:

Druckänderung
Übt man auf eine sich im Gleichgewicht befindliche Reaktion durch Druckänderung einen Zwang aus, weicht das System so aus, dass bei einer Erhöhung die volumenverkleinernde Reaktion gefördert wird und umgekehrt.
Die Reaktionsgleichung zeigt links vier Mol Gas und rechts zwei Mol Gas. Damit nimmt bei der Ammoniak-Synthese das Gesamtvolumen ab und eine Druckerhöhung führt zur Gleichgewichtsverschiebung auf die Seite der Produkte.

Temperaturänderung
Übt man auf eine sich im Gleichgewicht befindliche Reaktion durch Temperaturänderung einen Zwang aus, weicht das System so aus, dass bei einer Erhöhung die endotherme Reaktion gefördert wird und umgekehrt.
Die Ammoniak-Synthese ist exotherm. Damit führt eine Temperaturerhöhung zu einer Gleichgewichtsverschiebung auf die Seite der Produkte.

Die Tabelle zeigt:

Spalte mit $1\,\text{bar}:$ Die Synthese von Ammoniak bei einem Bar und verschiedenen Temperaturen zeigt, je höher die Temperatur wird, desto kleiner ist der prozentuale Volumenanteil des Produktes.

Zeile mit $200^{\circ}C:$ Die Synthese von Ammoniak bei $200^{\circ}C$ und verschiedenen Drücken zeigt, je höher der Druck, desto höher der Produktanteil.

Für eine hohe Ausbeute muss die Ammoniak-Synthese also bei möglichst niedrigen Temperaturen und möglichst hohen Drücken durchgeführt werden.

1.2

Stoffmengen an Wasserstoff und Stickstoff im Gleichgewicht

Ergebnis anzeigen

Die Aufgabenstellung zeigt, dass nach Gleichgewichtseinstellung $1,785\,\text{mol}$ Ammoniak vorliegen:

$2y = 1,785 \,\text{mol}$ $\quad \Leftrightarrow \quad$ $y = 0,8925 \,\text{mol}$

Demnach betragen die Gleichgewichtsstoffmengen:

$\begin{array}[t]{rll} n_{N_2}&=&(1 - 0,8925) \,\text{mol} & \\[5pt] &=& 0,1075\,\text{mol} \end{array}$

$\begin{array}[t]{rll} n_{H_2}&=&(3 - 3 \cdot 0,8925) \,\text{mol} & \\[5pt] &=& 0,3225\,\text{mol} \end{array}$

Stoffmengenanteil von Ammoniak im Gleichgewicht

In einer Mischung lässt sich für eine Komponente A der Stoffmengenanteil $x_\text{A}$ als den Quotienten aus der Stoffmenge A und der Gesamtstoffmenge aller Mischungsbestandteile definieren:

$x_A$ = $\dfrac{n_A} {\displaystyle\sum n_i}$

Der Stoffmengenanteil $x_\text{A}$ von Ammoniak im Gleichgewicht ist also:

Rechenweg anzeigen

$x_{NH_3} \approx 0,8059$

Zum Schluss wird das Ergebnis mit $100\,\%$ multipliziert und es ergibt sich ein Stoffmengenanteil von $x_{NH_3}$ $\approx 80,6\,\%.$

2.1

Grafische Darstellung der kalorimetrischen Daten

Beginn und Ende der Ammoniak-Verbrennung

Die Tabellendaten zeigen, dass die Temperatur im Kalorimeter ab zwei Minuten anfängt zu steigen. Der Beginn der Verbrennung fand demnach zwischen $1,5$ und $2$ Minuten statt.

Nach sieben Minuten wird das Maximum erreicht. Das Ende der Verbrennung liegt zeitlich kurz davor, was etwa $6,5$ Minuten entspricht.

Begründung der fallenden Temperatur

Idealen Kalorimeter geben die gesamte Verbrennungswärme an die Kalorimeterflüssigkeit ab, wodurch kein Wärmeverlust stattfindet. In der Realität nimmt das Kalorimeter jedoch immer eine gewisse Wärmemenge auf. Folglich nimmt die Temperatur der Kalorimeterflüssigkeit nach Ende des Experiments langsam ab.

Ermittlung der von Trichlormethan aufgenommenen Wärmemenge

Um die während der Verbrennung aufgenommene Wärmemenge zu bestimmen, wird die Temperaturkurve aus dem Versuch auf Basis der Flächengleichheit ausgewertet:

Anlegen von Ausgleichsgeraden durch die Daten jeweils zu Beginn und Ende der Messung.
Ziehen einer Linie, die diese Geraden und die Messkurve schneidet. Dabei sollen die eingeschlossenen Flächen I und II gleich groß sein
Die Schnittpunkte der Ausgleichsgeraden mit diesen Linien ergeben die Anfangs-bzw. Endtemperatur.
Die maximale Temperaturdifferenz ergibt sich aus der Differenz der $y$ -Werte;
hier: $8^{\circ}C$ oder $8\,\text{K}$

Nun folgt die Berechnung der vom Trichlormethan aufgenommenen Wärmemenge:

$\begin{array}[t]{rll} Q&=& C_{CHCl_3} \cdot M_{CHCl_3} \cdot \Delta T& \\[5pt] &=& 0,95 \,\text{J} \cdot \text{g}^{-1} \cdot \text{K}^{-1} \cdot 1000\,\text{g} \cdot 8\,\text{K} & \\[5pt] &=& 7600 \,\text{J} \end{array}$

2.2

Reaktionsenthalpie mit der experimentell bestimmten Wärmemenge $Q$

Folgende Werte sind gegeben:

$m_{NH_3} = 0,5 \,\text{g};$

$M_{NH_3} = 17 \,\text{g} \cdot \text{mol}^{-1} \quad;$

$\begin{array}[t]{rll} n_{NH_3}&=& \dfrac{0,5 \,\text{g}}{17 \,\text{g}\cdot \text{mol}^{-1} } & \\[5pt] &\approx& 0,0294 \end{array}$

Daraus folgt:

$\begin{array}[t]{rll} \Delta_cH_{NH_3}&=& -\dfrac{Q}{n_{NH_3}} & \\[5pt] &=& -\dfrac{9,5 \,\text{kJ}}{0,0294 \,\text{mol}} & \\[5pt] &\approx& -323,1 \,\text{kJ} \cdot \text{mol}^{-1} \end{array}$

Reaktionsenthalpie mit den thermodynamischen Daten

Für die Berechnung gilt:

Formel anzeigen

Aus der Reaktionsgleichung ergibt sich damit:

Rechnung anzeigen

$\Delta_rH^0 = -1532 \,\text{kJ} \cdot \,\text{mol}^{-1}$

Zuletzt muss die Verbrennungsenthalpie auf ein Mol Ammoniak bezogen werden:

$\begin{array}[t]{rll} \Delta_cH_{NH_3}&=& \dfrac{-1532 \,\text{kJ} \cdot \,\text{mol}^{-1}}{4}& \\[5pt] &=& -383 \,\text{kJ} \cdot \,\text{mol}^{-1} \end{array}$

Überprüfung der Aussagen

Es wurden unwissentlich mehr als $1 000 \,\text{g}$ Trichlormethan in die Apparatur gegeben.

Wenn im Kalorimeter mehr als die in der Rechnung eingesetzten $1000\,\text{g}$ Trichlormethan enthalten war, wäre der berechnete Wert für $Q$ zu klein und würde damit die Abweichung zwischen Fall A und Fall B erklären.

Ein Teil des entstehenden Wassers ist nicht kondensiert.

Phasenübergänge von gasförmigem zu flüssigem Wasser setzen Kondensationswärme frei. Wenn die gesamte freigesetzte Wassermenge nicht im Kalorimeter kondensieren würde, wäre die gemessene Wärmemenge zu klein. Damit würde sich für das Experiment der (betragsmäßig) zu kleine Wert der Reaktionsenthalpie erklären lassen.