Besondere Vierecke
Ein Viereck ist eine ebene Figur mit vier Ecken und vier Kanten. Die Innenwinkelsumme in einem Viereck beträgt  Diese Eigenschaften gelten für jedes Viereck. Es gibt jedoch Spezialfälle, in denen Vierecke Eigenschaften haben, die nicht für jedes Viereck gelten. Diese Vierecke heißen besondere Vierecke. Aber was sind besondere Vierecke bzw. welche Vierecke gibt es?
Diese Eigenschaften gelten für jedes Viereck. Es gibt jedoch Spezialfälle, in denen Vierecke Eigenschaften haben, die nicht für jedes Viereck gelten. Diese Vierecke heißen besondere Vierecke. Aber was sind besondere Vierecke bzw. welche Vierecke gibt es?
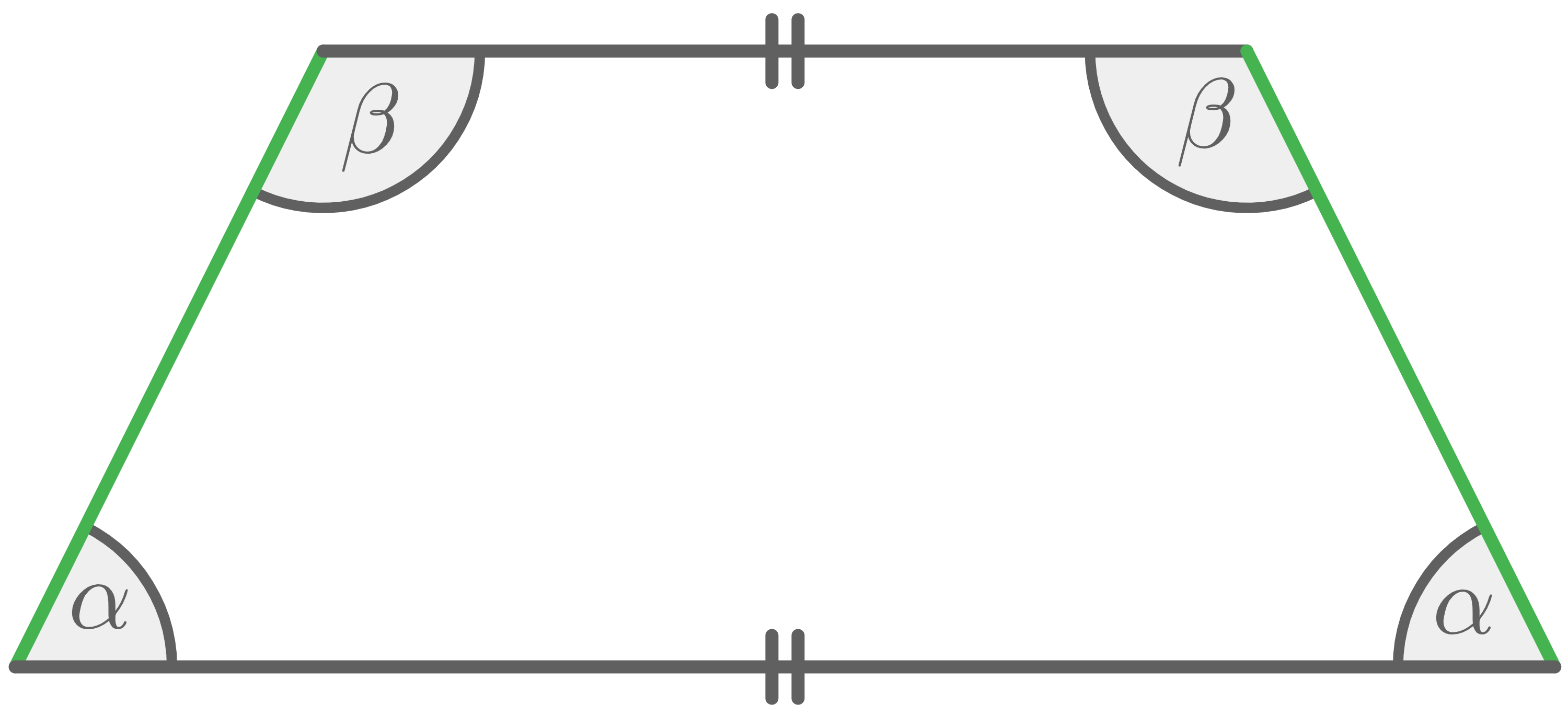
 Eine speziellere Form des Trapezes ist das gleichschenklige Trapez. Dieses besondere Viereck hat die folgenden Eigenschaften:
Eine speziellere Form des Trapezes ist das gleichschenklige Trapez. Dieses besondere Viereck hat die folgenden Eigenschaften:

 Bildnachweise [nach oben]
Bildnachweise [nach oben]
Vierecke Arten
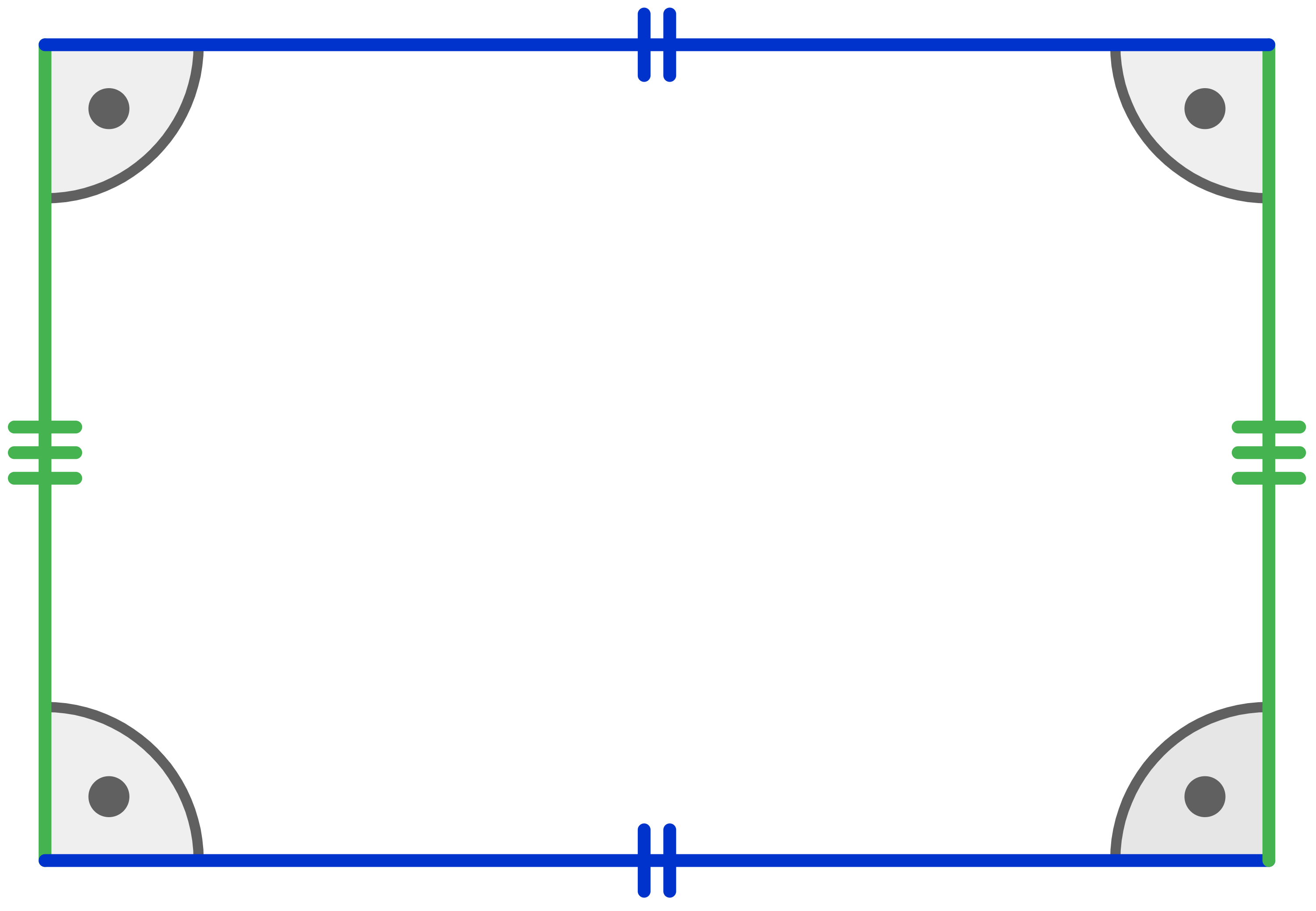
Es gibt viele verschiedene besondere Vierecke, die ganz spezielle Eigenschaften haben. Dazu zählen Rechteck, Quadrat, Parallelogramm, Raute, Drachen und Trapez. Besondere Vierecke schließen sich nicht gegenseitig aus, so ist beispielsweise jedes Quadrat auch automatisch ein Rechteck. Welche Eigenschaften jedes besondere Viereck hat wird im Folgenden beschrieben. In den folgenden Abbildungen werden Seiten mit gleicher Länge durch gleiche Farben und parallele Seiten durch eine gleiche Anzahl an Querstrichen gekennzeichnet.Rechteck Eigenschaften
Was ist ein Rechteck? Rechtecke sind besondere Vierecke mit den folgenden Eigenschaften:
- alle Winkel haben
- gegenüberliegende Seiten sind gleich lang
- gegenüberliegende Seiten sind parallel

Rechteck
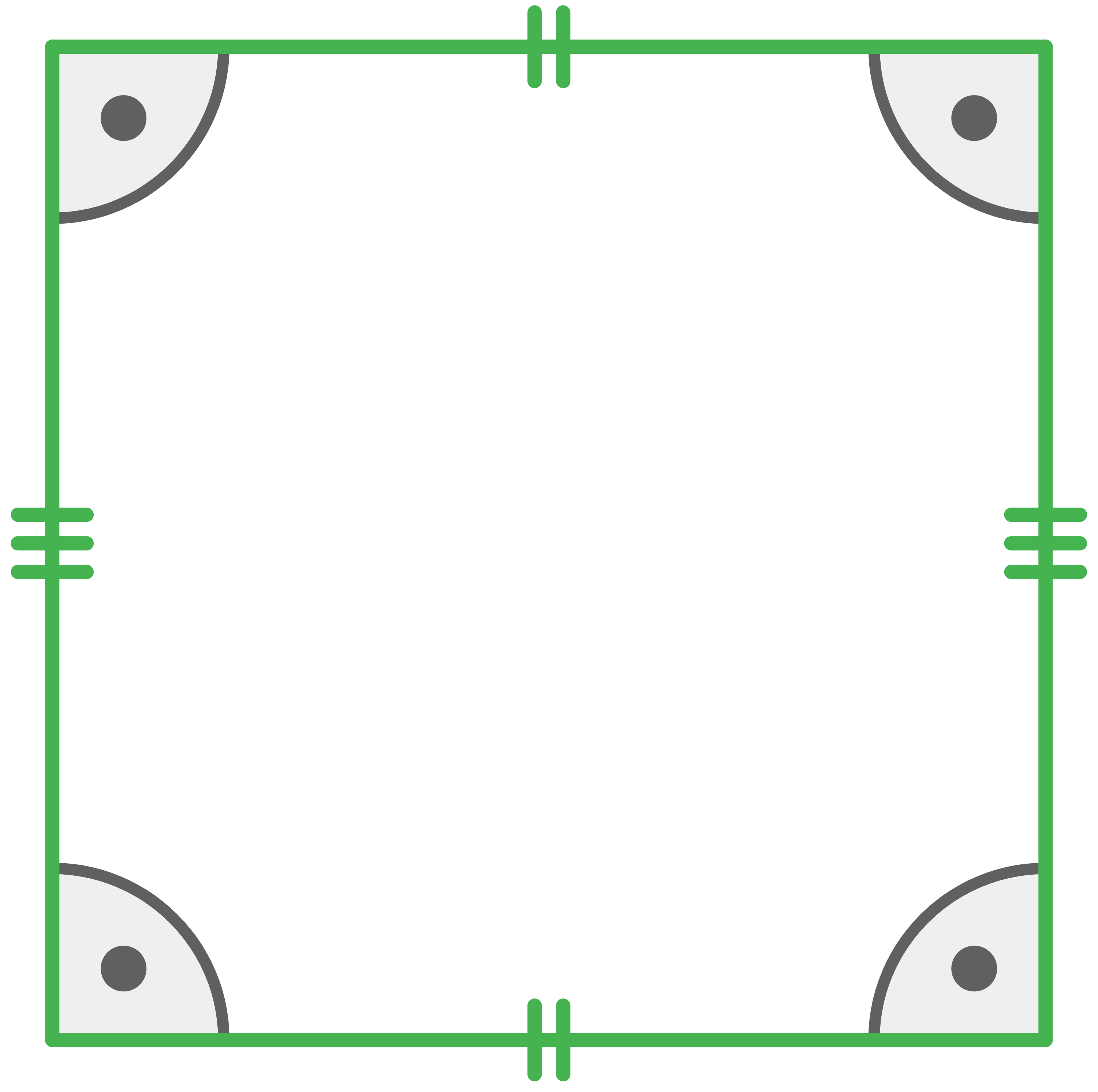
Quadrat Eigenschaften
Ein Quadrat hat die gleichen Eigenschaften wie ein Rechteck. Dieses besondere Viereck unterscheidet sich vom Rechteck jedoch in der weiteren Eigenschaft, dass nicht nur die gegenüberliegenden Seiten, sondern alle Seiten des Vierecks gleich lang sind. Ein Quadrat hat also folgende Eigenschaften:
- alle Winkel haben
- alle Seiten sind gleich lang
- gegenüberliegende Seiten sind parallel

Quadrat
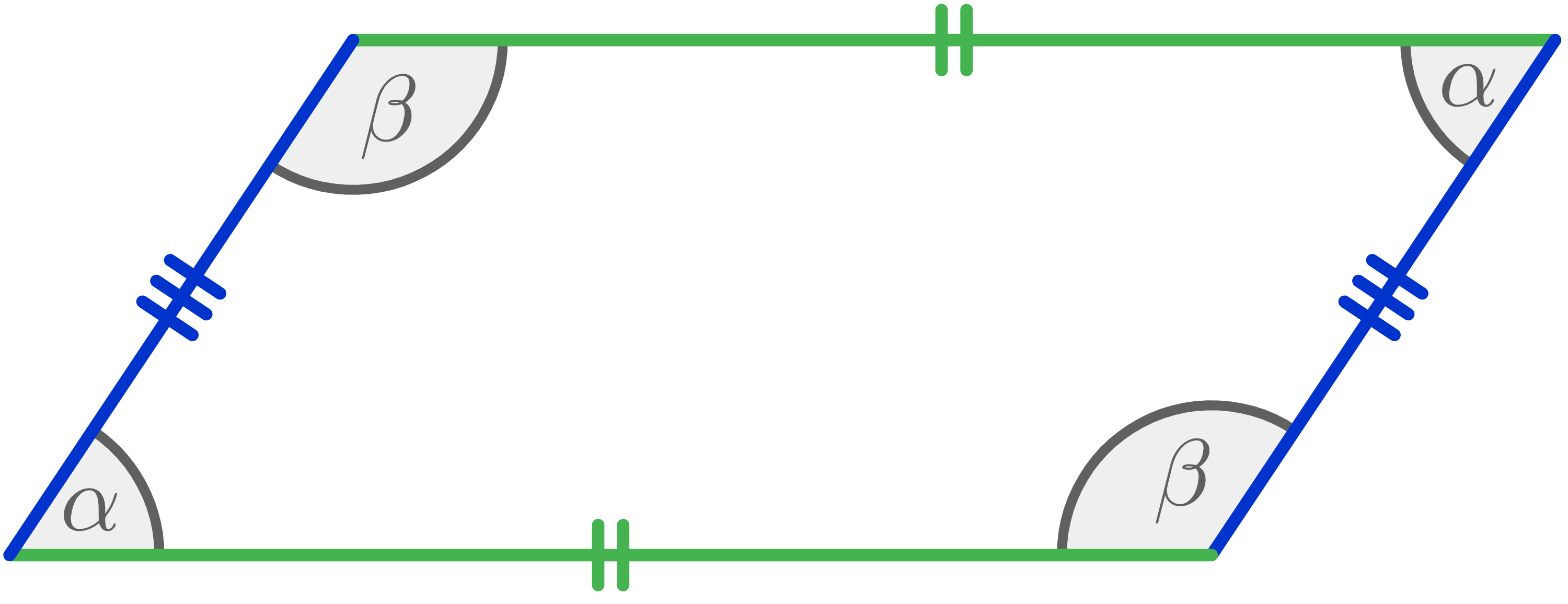
Parallelogramm Eigenschaften
Was ist ein Parallelogramm? Parallelogramme sind besondere Vierecke, die die folgenden Eigenschaften haben:
Ein Parallelogramm ist wie ein Rechteck, bei dem die obere Kante hin und her bewegt wurde. Dadurch bleiben gegenüberliegende Seiten gleich lang und gegenüberliegende Winkel bleiben gleich groß, aber im Unterschied zum Rechteck haben die Winkel im Allgemeinen nicht mehr Ein Rechteck ist sozusagen ein Spezialfall eines Parallelogramms, bei dem alle Winkel
Ein Rechteck ist sozusagen ein Spezialfall eines Parallelogramms, bei dem alle Winkel  haben.
haben.
- gegenüberliegende Seiten sind gleich lang
- gegenüberliegende Winkel sind gleich groß
- gegenüberliegende Seiten sind parallel
Ein Parallelogramm ist wie ein Rechteck, bei dem die obere Kante hin und her bewegt wurde. Dadurch bleiben gegenüberliegende Seiten gleich lang und gegenüberliegende Winkel bleiben gleich groß, aber im Unterschied zum Rechteck haben die Winkel im Allgemeinen nicht mehr

Parallelogramm
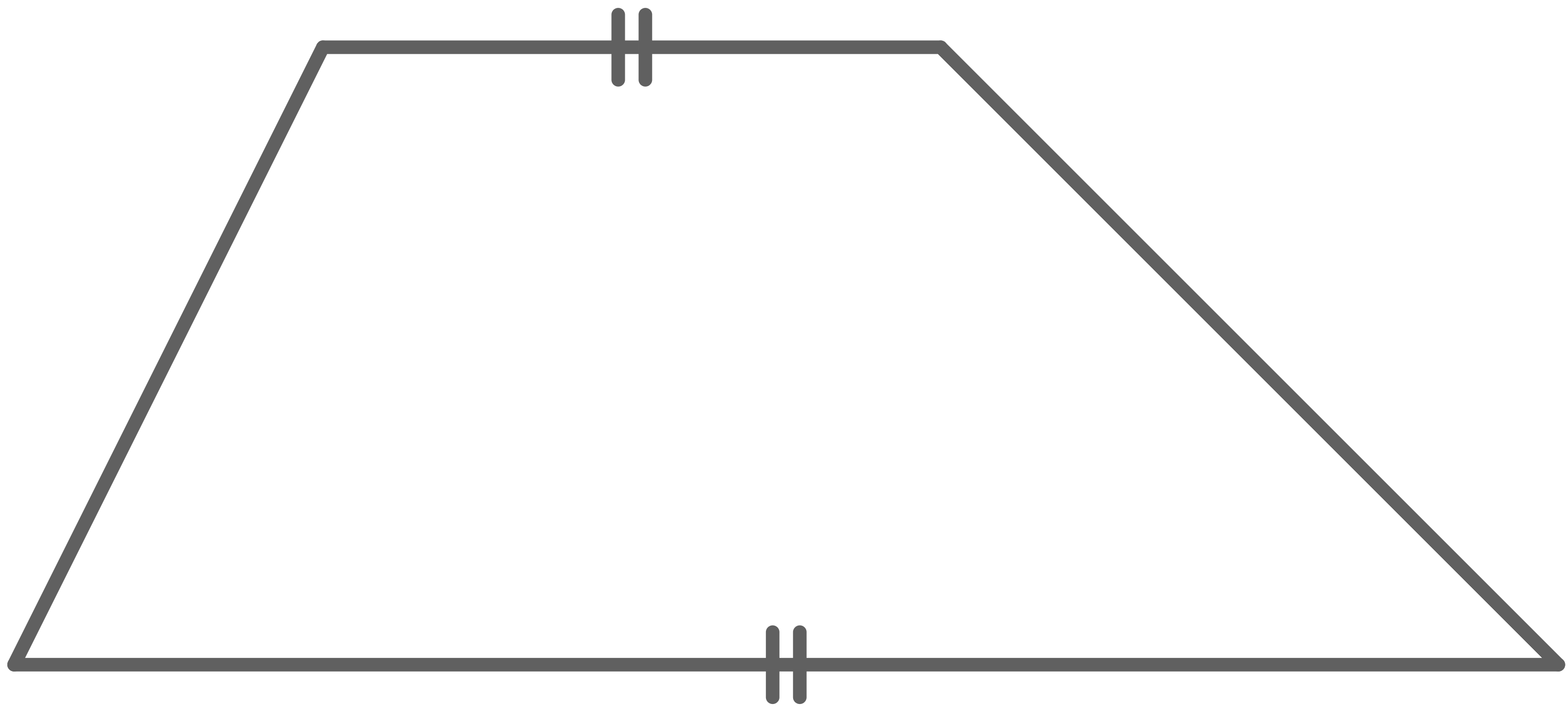
Trapez Eigenschaften
Das besondere Viereck mit folgender Eigenschaft wird Trapez genannt:
- ein Paar gegenüberliegender Seiten ist parallel

Trapez
- ein Paar gegenüberliegender Seiten ist parallel
- die beiden Schenkel sind gleich lang und nur dann parallel, wenn das Viereck ein Rechteck ist

Gleichschenkliges Trapez
Raute Eigenschaften
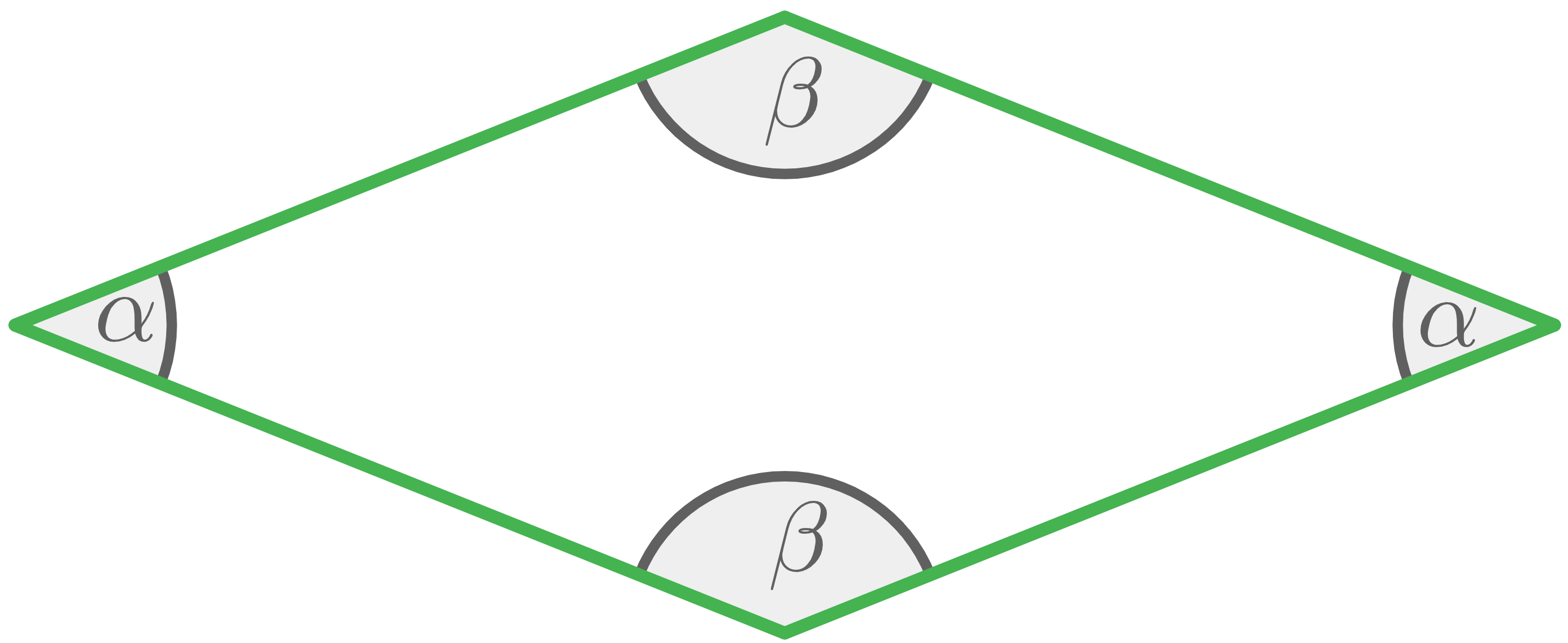
Was ist eine Raute? Besondere Vierecke mit folgenden Eigenschaften heißen Raute:
- alle vier Seiten sind gleich lang
- gegenüberliegende Seiten sind parallel
- gegenüberliegende Winkel sind gleich groß

Raute
Drache Eigenschaften
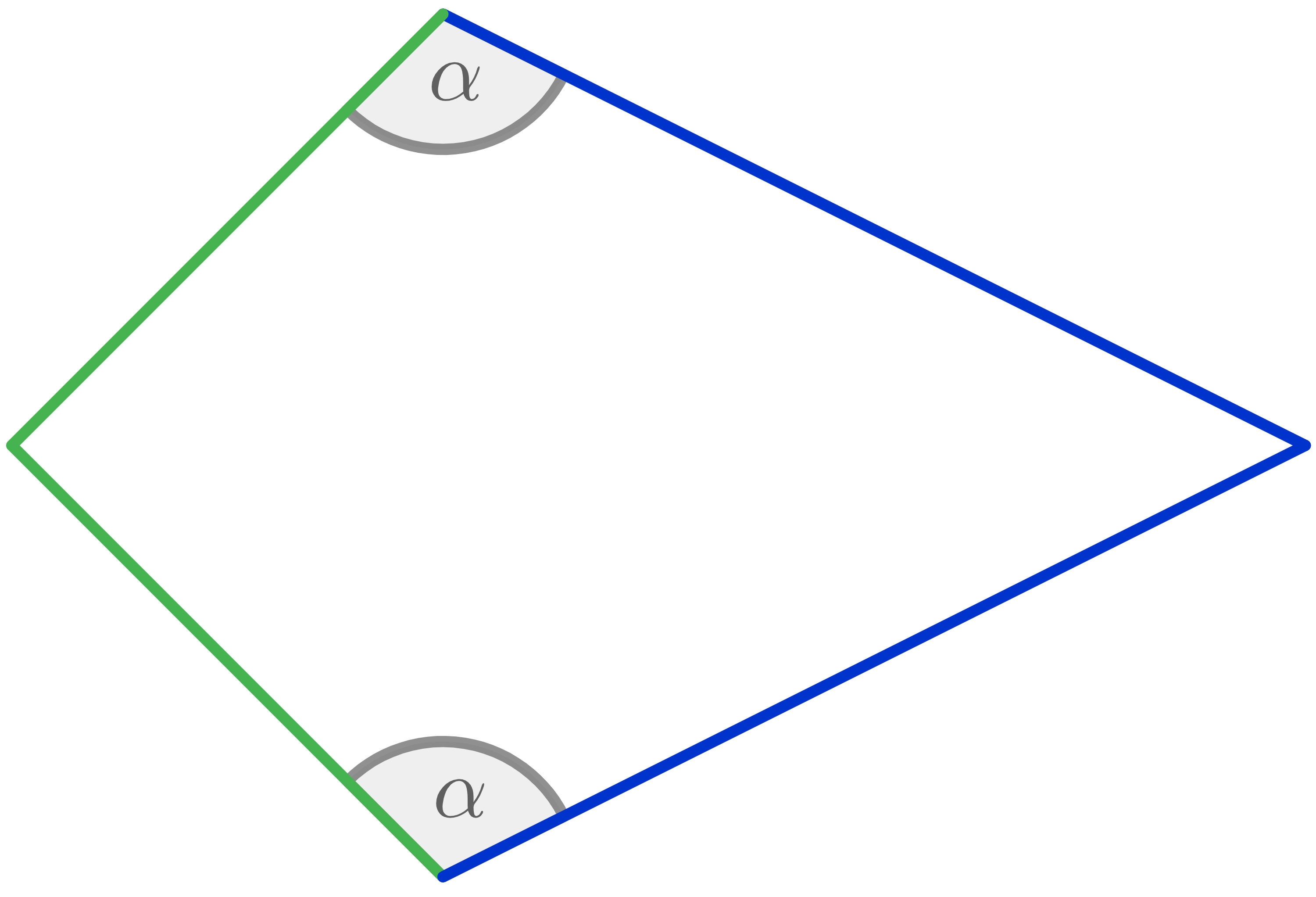
Ein Drachen ist ein besonderes Viereck mit den folgenden Eigenschaften:
Unterschied Drachen Raute: Da bei einem Drachen im Unterschied zur Raute nicht alle Seiten gleich lang sein müssen, sind gegenüberliegende Seiten nicht unbedingt gleich lang und gegenüberliegende Winkel nicht gleich groß. Falls dies doch der Fall ist, so handelt es sich um den Spezialfall eines Drachens, nämlich die Raute. Diese ist also auch ein Drachen, bei dem speziell alle vier Seiten gleich lang sind.
- jeweils zwei benachbarte Seiten sind gleich lang
- ein Paar gegenüberliegender Winkel ist gleich groß
Unterschied Drachen Raute: Da bei einem Drachen im Unterschied zur Raute nicht alle Seiten gleich lang sein müssen, sind gegenüberliegende Seiten nicht unbedingt gleich lang und gegenüberliegende Winkel nicht gleich groß. Falls dies doch der Fall ist, so handelt es sich um den Spezialfall eines Drachens, nämlich die Raute. Diese ist also auch ein Drachen, bei dem speziell alle vier Seiten gleich lang sind.

Drachen
Aufgaben besondere Vierecke
1.
Gib jeweils den vierten Eckpunkt an, sodass die angegebenen besonderen Vierecke entsteht:
a)
Quadrat: 


b)
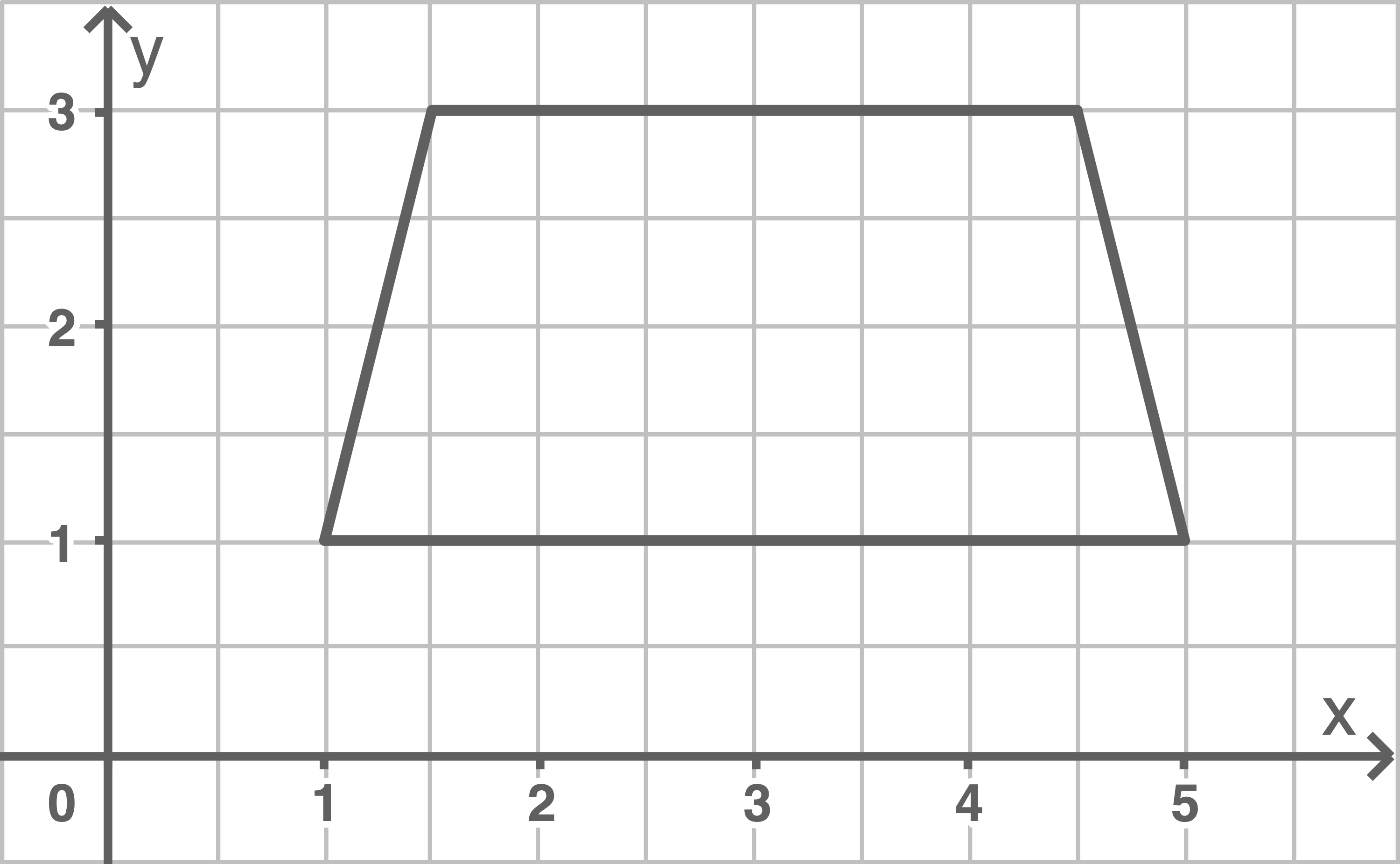
Gleichschenkliges Trapez: 


c)
Drachen: 


2.
Zeichne für folgende besondere Vierecke alle Symmetrieachsen ein:
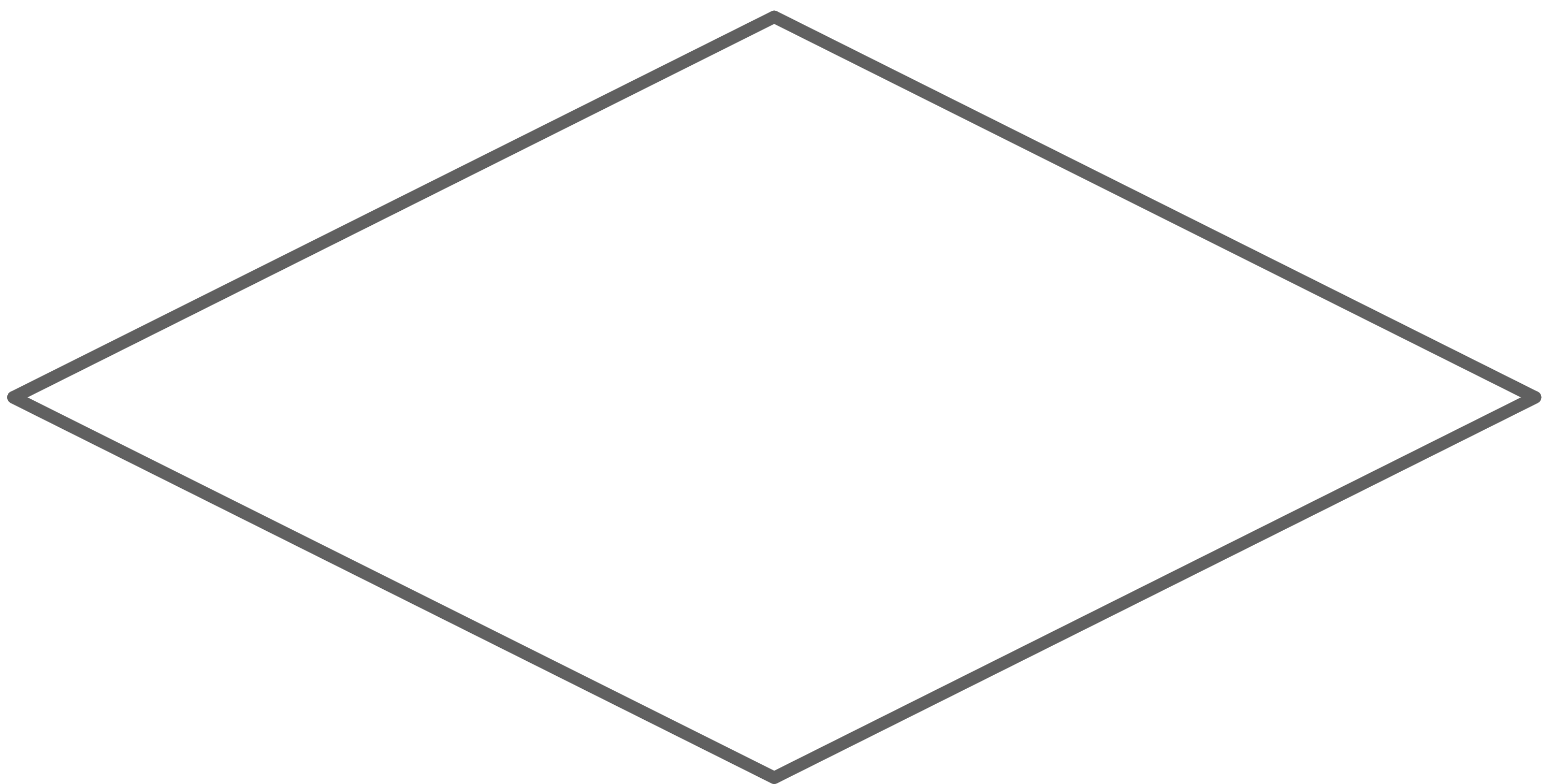


a)

Raute
b)

Parallelogramm
c)

Quadrat
3.
Nenne alle möglichen Bezeichnungen für die folgenden besonderen Vierecke:
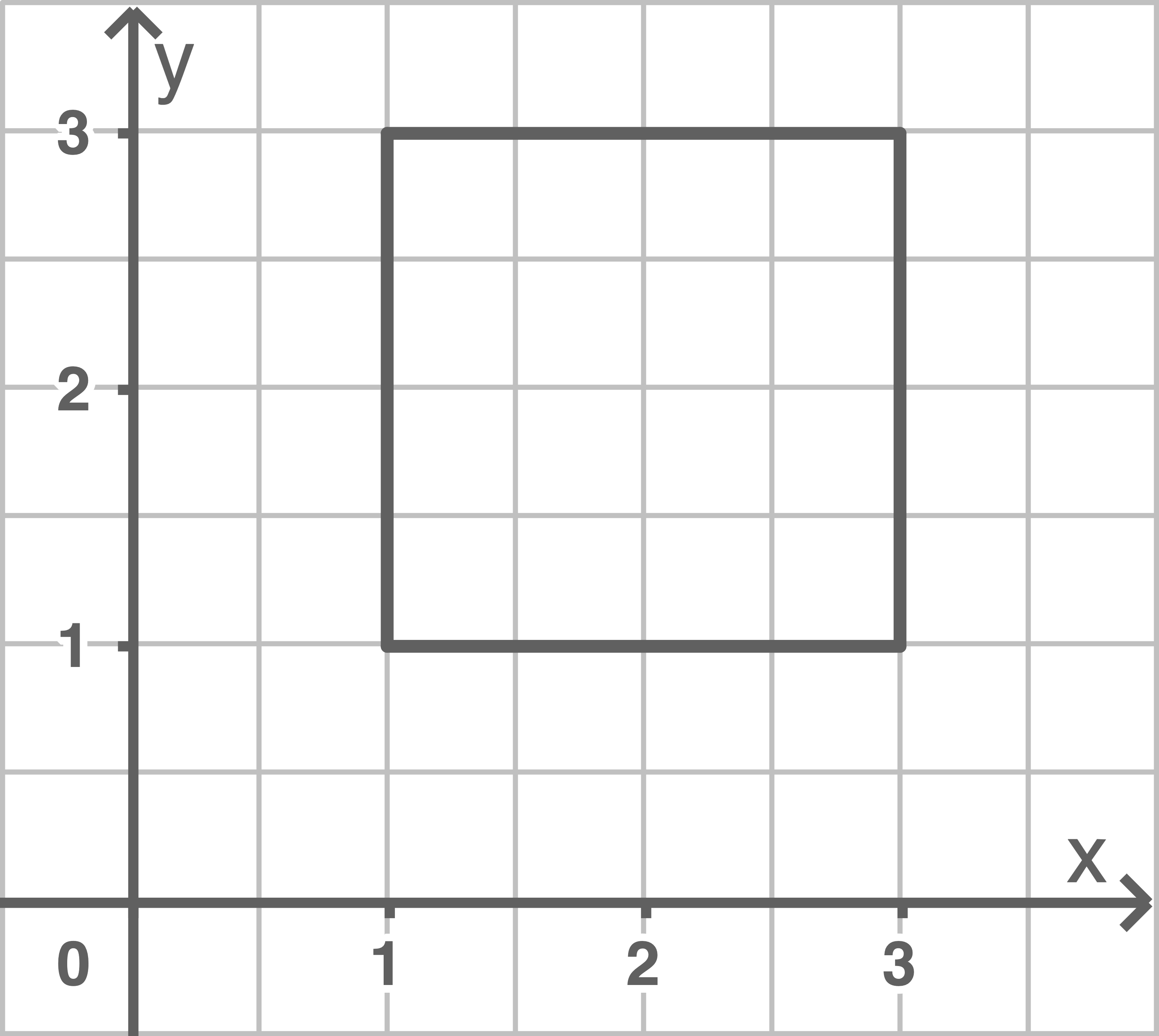
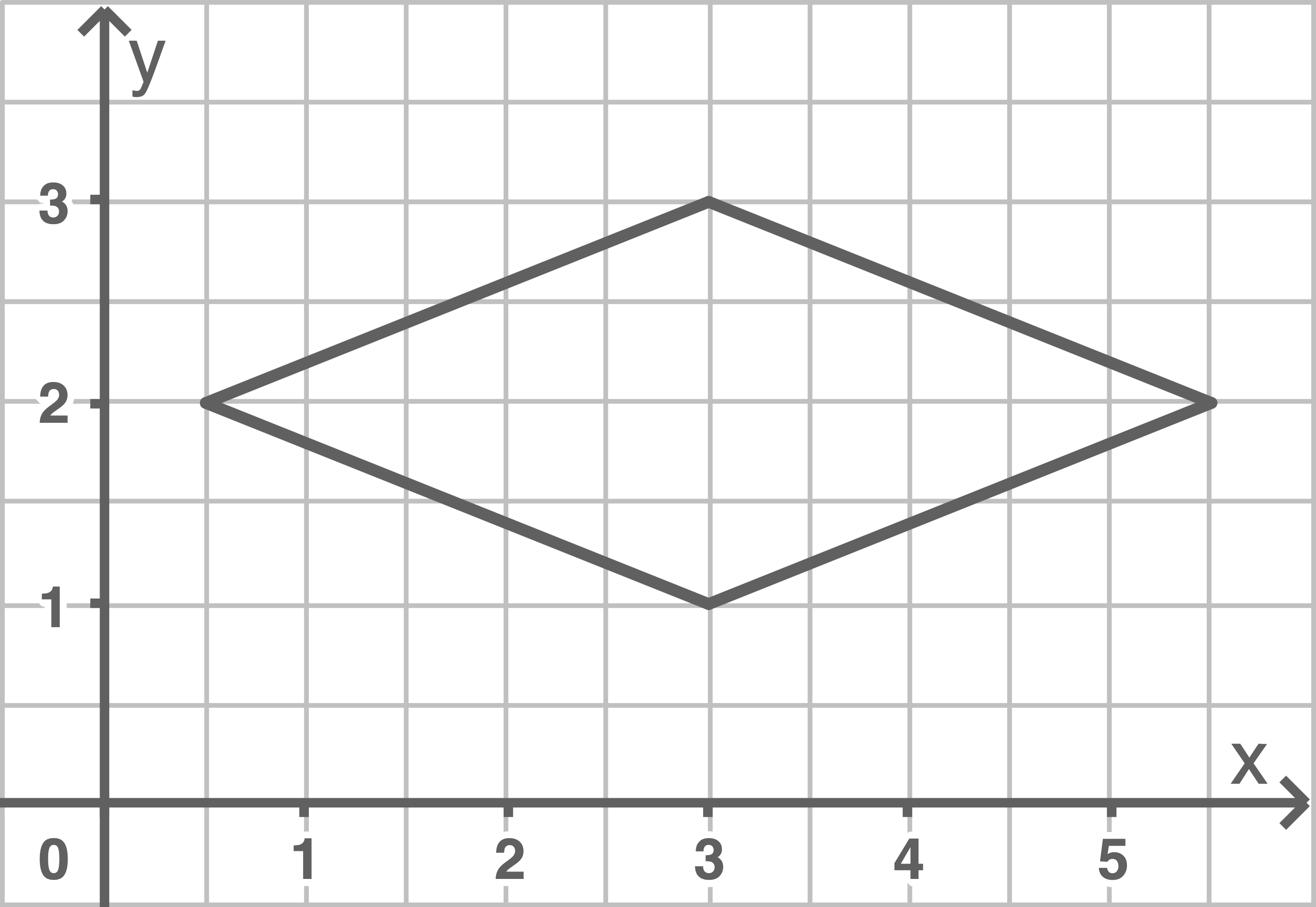
a)

b)

c)

Lösungen besondere Vierecke
1.
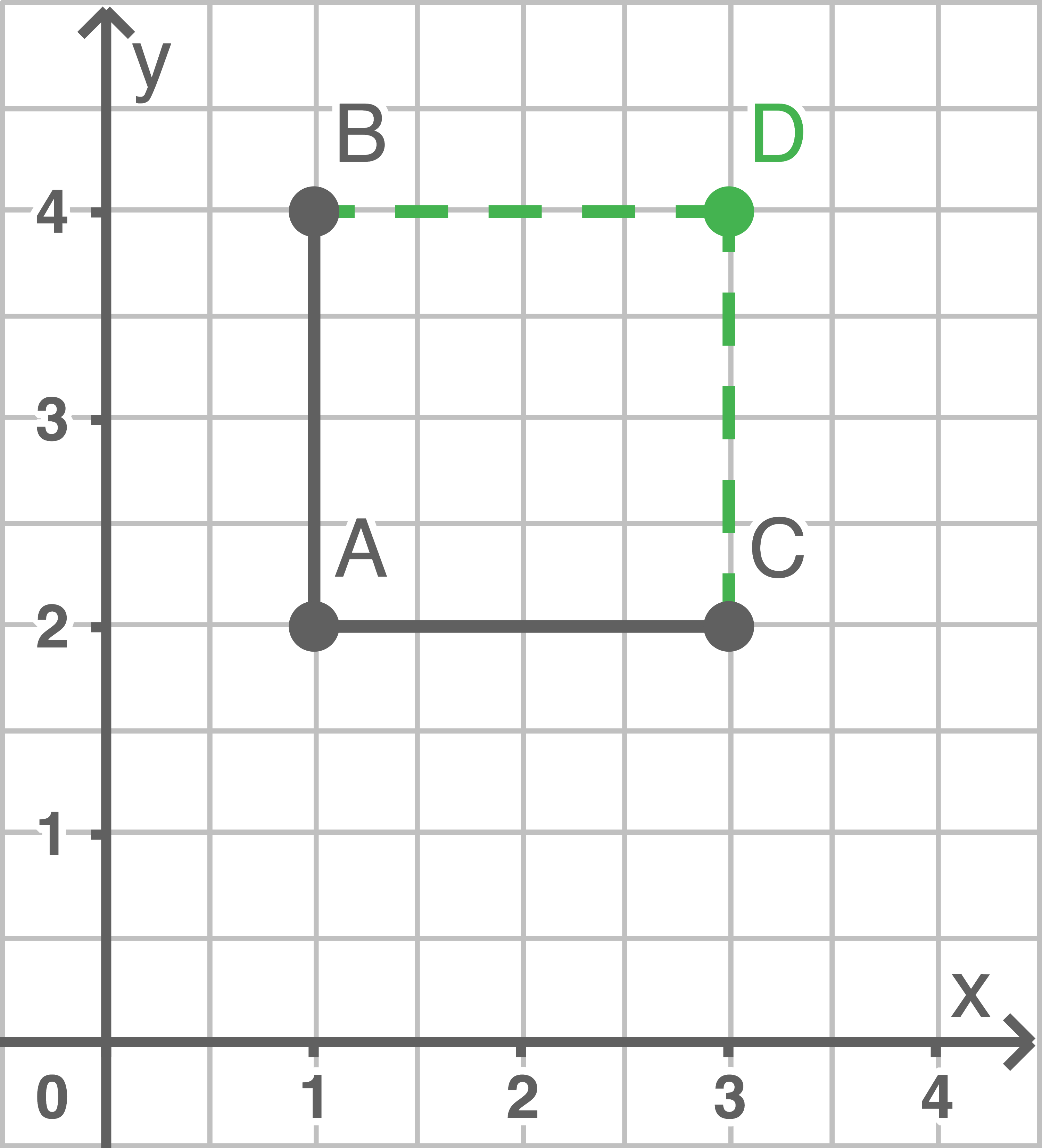
Am einfachsten ist es, die gegebenen Koordinaten in ein Koordinatensystem einzutragen und dann anschließend zu den besonderen Vierecken zu ergänzen.
a)
Da bei einem Quadrat alle Seiten gleich lang und gegebüberliegende Seiten parallel sein müssen, kommt nur der Punkt  infrage, um das gesuchte besondere Viereck zu erhalten.
infrage, um das gesuchte besondere Viereck zu erhalten.

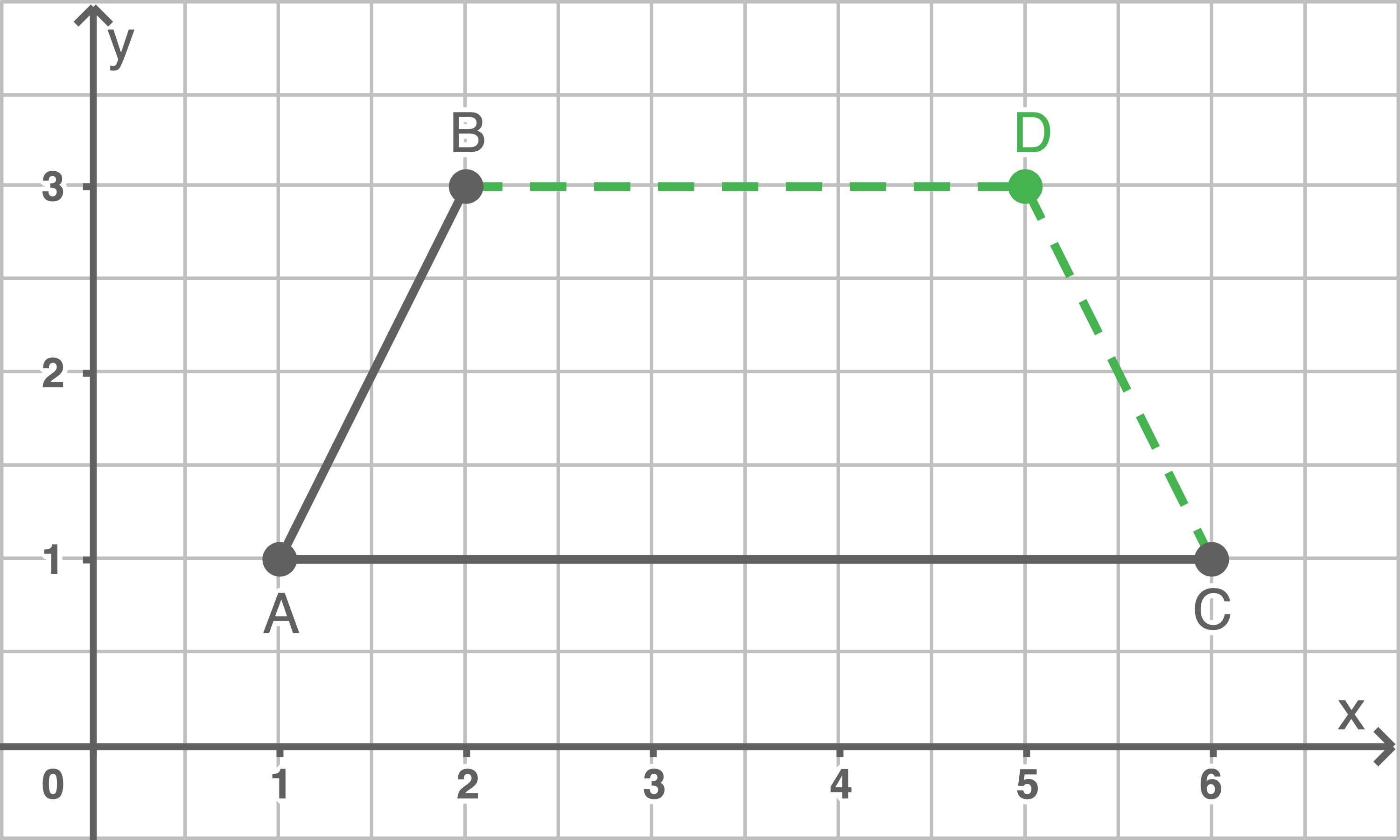
b)
Das besondere Viereck muss ein Paar paralleler und ein Paar gleich langer Seiten haben, die nicht parallel sind. Wählt man den Punkt  so, dass
so, dass  parallel zu
parallel zu  ist, gibt es noch zwei Möglichkeiten, die Koordinaten von
ist, gibt es noch zwei Möglichkeiten, die Koordinaten von  zu wählen, dass die Strecke
zu wählen, dass die Strecke  gleich lang ist wie
gleich lang ist wie  ohne dass die Strecken parallel zueinander sind. Die gesuchten Koordinaten lauten
ohne dass die Strecken parallel zueinander sind. Die gesuchten Koordinaten lauten 

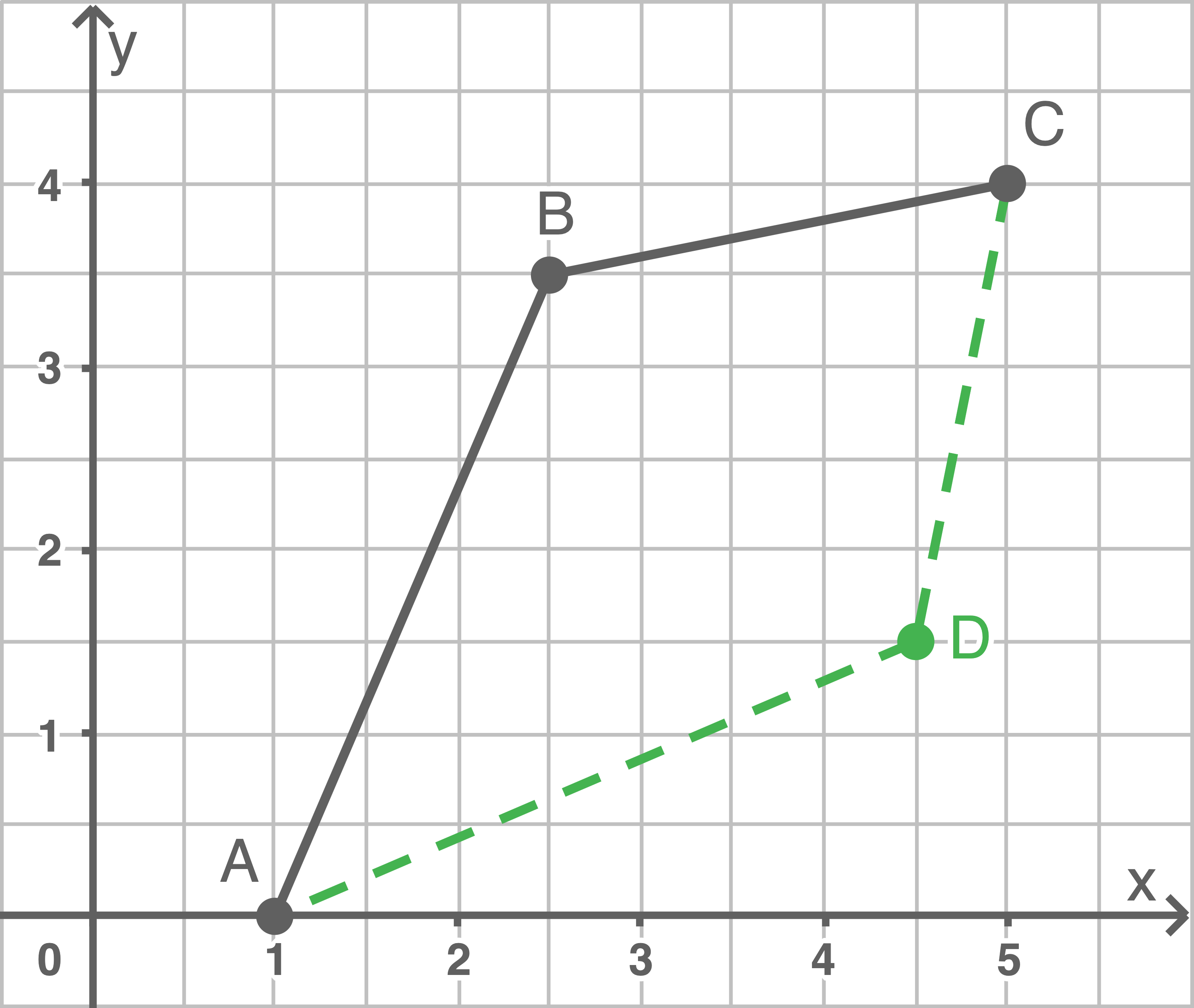
c)
Bei einem Drachen müssen jeweils zwei benachbarte Seiten gleich lang sein. Da die Strecke  offensichtlich länger als die Strecke
offensichtlich länger als die Strecke  ist, müssen folglich
ist, müssen folglich  und
und  sowie
sowie  und
und  jeweils gleich lang sein. Dies kann man am besten erreichen, indem man die Kästchen in die jeweiligen Richtungen abzählt. Der Punkt
jeweils gleich lang sein. Dies kann man am besten erreichen, indem man die Kästchen in die jeweiligen Richtungen abzählt. Der Punkt  für den beide fehlenden Strecken die gesucht Länge haben, hat die Koordinaten
für den beide fehlenden Strecken die gesucht Länge haben, hat die Koordinaten 

2.
a)
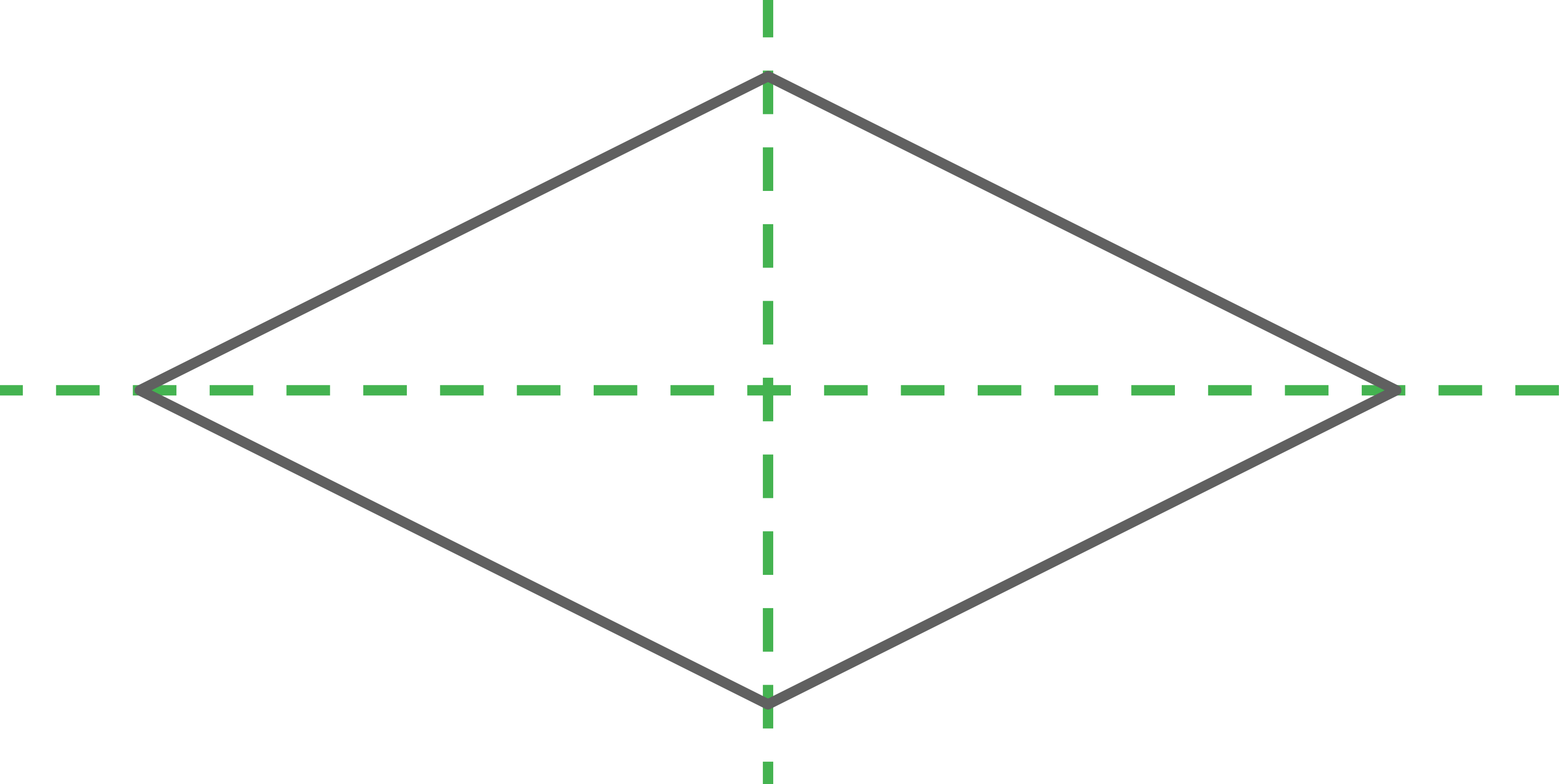
Die Raute hat zwei Symmetrieachsen, die durch ihre Diagonalen gegeben sind.

Symmetrieachsen Raute
b)
Ein Parallelogramm hat im Allgemeinen keine Symmetrieachsen. Der Spezialfall, in dem es zwei Symmetrieachsen hat, ist wenn das Parallelogramm gleichzeitig eine Raute ist. In diesem Fall sind die Symmetrieachsen wie in Aufgabe a) gegeben.

Symmetrieachsen Parallelogramm
c)
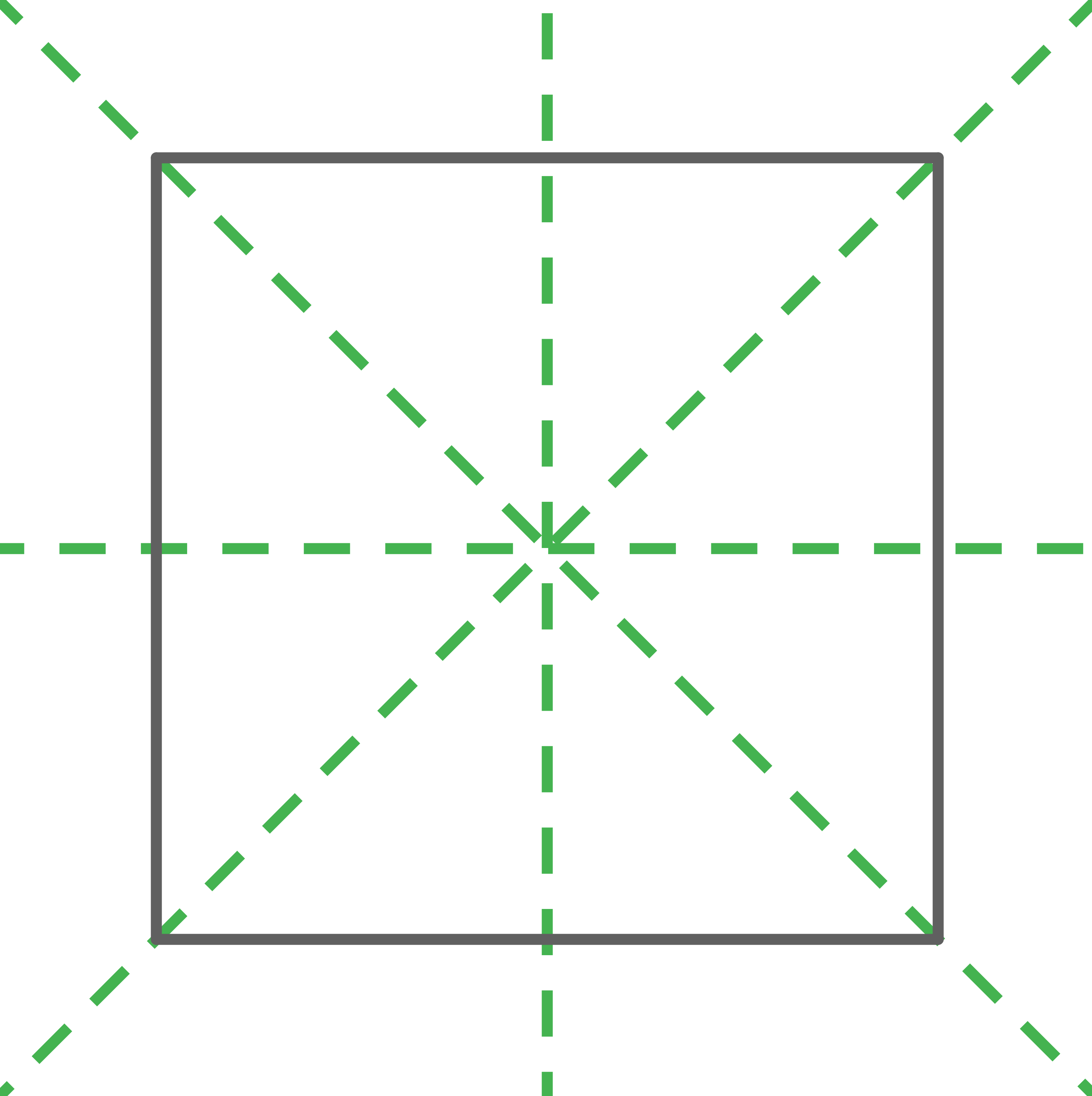
Jedes Quadrat hat vier Symmetrieachsen. Zwei davon sind durch die Diagonalen, die anderen beiden durch die Mittelparallelen gegeben.

Symmetrieachsen Quadrat
3.
a)
Quadrat: Alle Seiten sind gleich lang und die Winkel haben alle  Rechteck: Gegenüberliegende Seiten sind gleich lang und und alle Winkel haben
Rechteck: Gegenüberliegende Seiten sind gleich lang und und alle Winkel haben  Raute: Alle vier Seiten sind gleich lang.
Trapez: Es gibt ein Paar gegenüberliegender Seiten, die parallel zueinander sind. Da beide Schenkel außerdem gleich lang sind, handelt es sich sogar um ein gleichschenkliges Trapez.
Parallelogramm: Gegenüberliegende Seiten sind gleich lang.
Raute: Alle vier Seiten sind gleich lang.
Trapez: Es gibt ein Paar gegenüberliegender Seiten, die parallel zueinander sind. Da beide Schenkel außerdem gleich lang sind, handelt es sich sogar um ein gleichschenkliges Trapez.
Parallelogramm: Gegenüberliegende Seiten sind gleich lang.
b)
Raute: Alle Seiten sind gleich lang.
Parallelogramm: Gegenüberliegende Seiten sind gleich lang.
Trapez: Es gibt ein Paar gegenüberliegender Seiten, die parallel zueinander sind.
Drachen: Jeweils zwei benachbarte Seiten sind gleich lang.
c)
Trapez: Es gibt ein Paar gegenüberliegender Seiten, die parallel zueinander sind. Da beide Schenkel außerdem gleich lang sind, handelt es sich sogar um ein gleichschenkliges Trapez.
© - SchulLV.
Einführungsaufgabe
Ordne den Figuren einen Namen zu, der sie möglichst eindeutig beschreibt.Aufgabe 1
Entscheide, ob folgende Aussagen richtig oder falsch sind.| Aussage | R | F |
|---|---|---|
| Ein Parallelogramm besitzt vier Ecken. | ||
| Ein Parallelogramm ist ein Rechteck. | ||
| Ein Rechteck ist ein Parallelogramm. | ||
| Die Seiten einer Raute sind alle gleich lang. | ||
| Alle gegenüberliegenden Seiten eines Trapezes sind parallel. | ||
| Ein Drache ist ein Parallelogramm. | ||
| Die Seiten eines Quadrates stehen senkrecht aufeinander. |
Aufgabe 2
Vervollständige die Figuren zu Parallelogrammen.Aufgabe 3
a)
Zeichne ein Parallelogramm, dass vier Seiten mit einer Länge von je  besitzt. Die Seiten des Parallelogramms stehen senkrecht aufeinander.
besitzt. Die Seiten des Parallelogramms stehen senkrecht aufeinander.
b)
Gib an, um welchen Spezialfall es sich bei dem Viereck aus a) handelt.
c)
Berechne den Umfang der Figur.
Aufgabe 4
Beantworte die Fragen und begründe deine Entscheidung.- Handelt es sich bei der abgebildeten Figur um ein Rechteck?
- Handelt es sich bei der abgebildeten Figur um ein Quadrat?
- Handelt es sich bei der abgebildeten Figur um eine Raute?
- Handelt es sich bei der abgebildeten Figur um ein Parallelogramm?
Aufgabe 5
Ergänze das abgebildete Dreieck zu einem Parallelogramm.Aufgabe 6
Zeichne einen Drachen
© - SchulLV.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Einführungsaufgabe
- Ein Viereck, das zwei benachbarte Seitenpaare mit jeweils gleicher Länge besitzt, wird Drache genannt.
- Ein Viereck mit zwei gleich langen Seitenpaaren, die zueinander parallel liegen heißt Parallelogramm.
- Stehen die Seiten eines solchen Parallelogramms senkrecht aufeinander, wird die Figur auch Rechteck genannt.
- Sind alle Seiten eines Rechtecks gleich lang, spricht man von einem Quadrat.
- Wenn die Seiten eines Vierecks alle gleich lang sind, die Seiten aber nicht senkrecht aufeinander stehen, so spricht man von einer Raute.
- Ein Trapez ist ein Viereck, das ein paralleles Seitenpaar mit unterschiedlicher Seitenlänge besitzt. Außerdem gibt es zwei gleich lange Seiten, die aber nicht parallel zueinander stehen.
Aufgabe 1
- Die Aussage „Ein Parallelogramm besitzt vier Ecken “ ist richtig.
- Die Aussage „Ein Parallelogramm ist ein Rechteck “ ist falsch. Bei einem Rechteck stehen die Seiten orthogonal zueinander. Dies ist bei einem Parallelogramm nicht immer der Fall.
- Die Aussage „Ein Rechteck ist ein Parallelogramm “ ist richtig. Bei einem Rechteck gibt es zwei Seitenpaare, die gleich lang und parallel zueinander sind.
- Die Aussage „Die Seiten einer Raute sind alle gleich lang “ ist richtig.
- Ein Trapez besitzt nur ein Seitenpaar mit zueinander parallelen Seiten. Die Aussage „Alle gegenüberliegenden Seiten eines Trapezes sind parallel“ ist falsch.
- Ein Drache ist kein Parallelogramm, da gegenüberliegende Seiten nicht gleich lang sind.
- Die Aussage „Die Seiten eines Quadrates stehen senkrecht aufeinander“ ist richtig.
Aufgabe 2
Aufgabe 3
a)
b)
c)
Aufgabe 4
- Die abgebildete Figur ist kein Rechteck, denn die Seiten stehen nicht senkrecht aufeinander.
- Die abgebildete Figur ist kein Quadrat, denn die Seiten stehen nicht senkrecht aufeinander.
- Die abgebildete Figur ist eine Raute, da alle Seiten gleich lang sind und gegenüberliegende Seiten parallel sind.
- Die abgebildete Figur ist ein Parallelogramm, da gegenüberliegende Seiten gleich lang sind und parallel verlaufen.
Aufgabe 5
Aufgabe 6
© - SchulLV.














