Trigonometrie im Raum
In Körpern können rechtwinklige Dreiecke als Hilfsdreiecke genutzt werden, um Berechnungen durchzuführen.
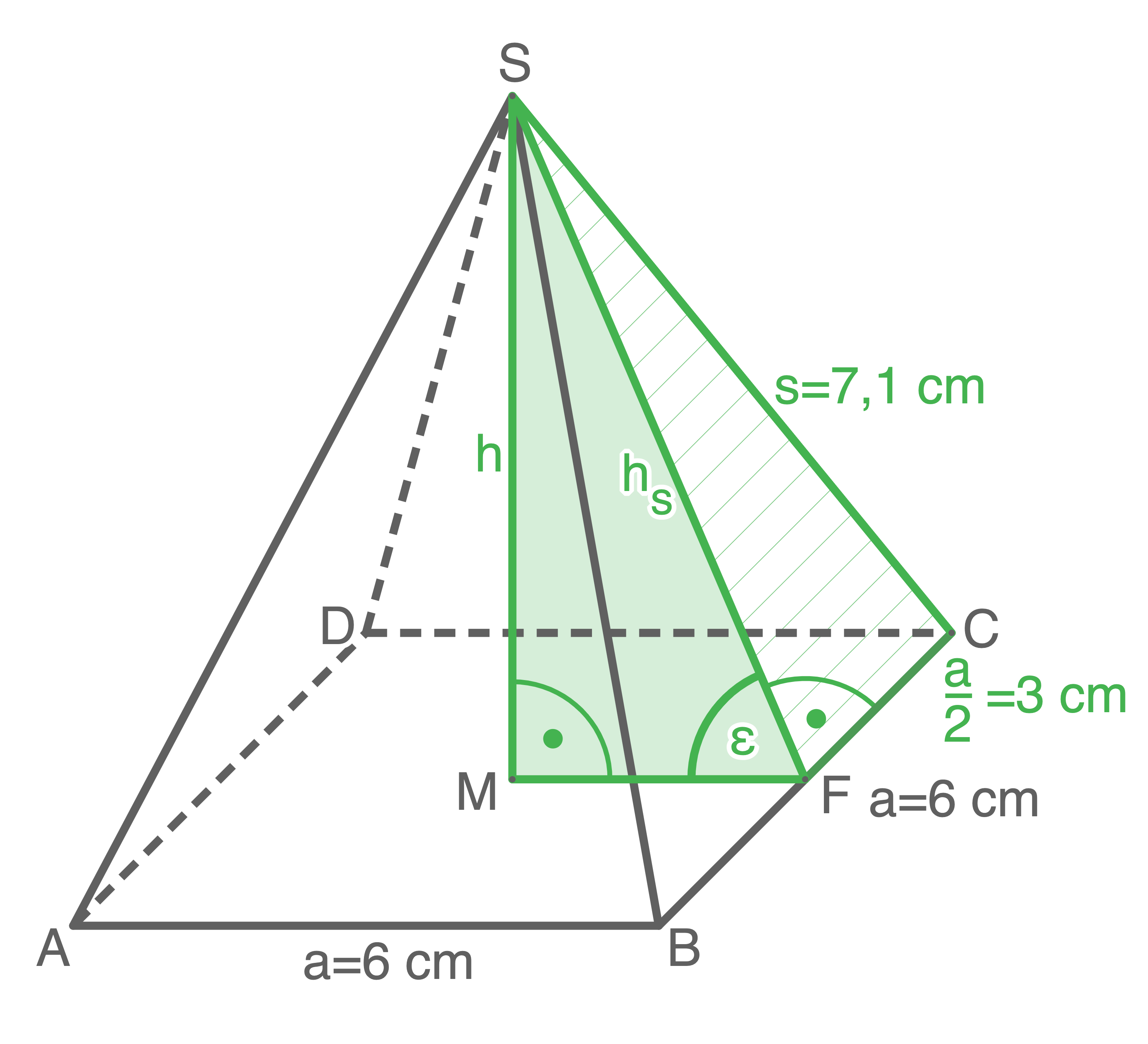1. Schritt: Länge von 
berechnen
![\(\begin{array}[t]{rll}
h_s^2+\left(\dfrac{a}{2}\right)^2&=&s^2 \quad \scriptsize \mid\;-\left(\dfrac{a}{2}\right)^2\\[5pt]
h_s^2&=&s^2-\left(\dfrac{a}{2}\right)^2 \quad \scriptsize \mid\;\sqrt{\,\,\,}\\[5pt]
h_s&=&\sqrt{s^2-\left(\dfrac{a}{2}\right)^2}\\[5pt]
&=&\sqrt{(7,1\,\text{cm})^2-\left(\dfrac{6\,\text{cm}}{2}\right)^2}\\[5pt]
h_s&=&6,4\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/d80261ee6f81e1fceec19c6e32daf73234767fa361ac30048b0521deca25c14d?color=5a5a5a)
2. Schritt: Länge von 
berechnen
![\(\begin{array}[t]{rll}
h^2 + \left(\dfrac{a}{2}\right)^2&=& h_s^2 \quad \scriptsize \mid\;-\left(\dfrac{a}{2}\right)^2 \\[5pt]
h^2&=&h_s^2-\left(\dfrac{a}{2}\right)^2 \quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
h&=&\sqrt{h_s^2-\left(\dfrac{a}{2}\right)^2}\\[5pt]
&=&\sqrt{(6,4\,\text{cm})^2-\left(\dfrac{6\,\text{cm}}{2}\right)^2}\\[5pt]
h&=&5,7\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/b65f22898497e7862790892ff04b22c682bd833b99b8ac0eeda581242b60387f?color=5a5a5a)
Beispiel
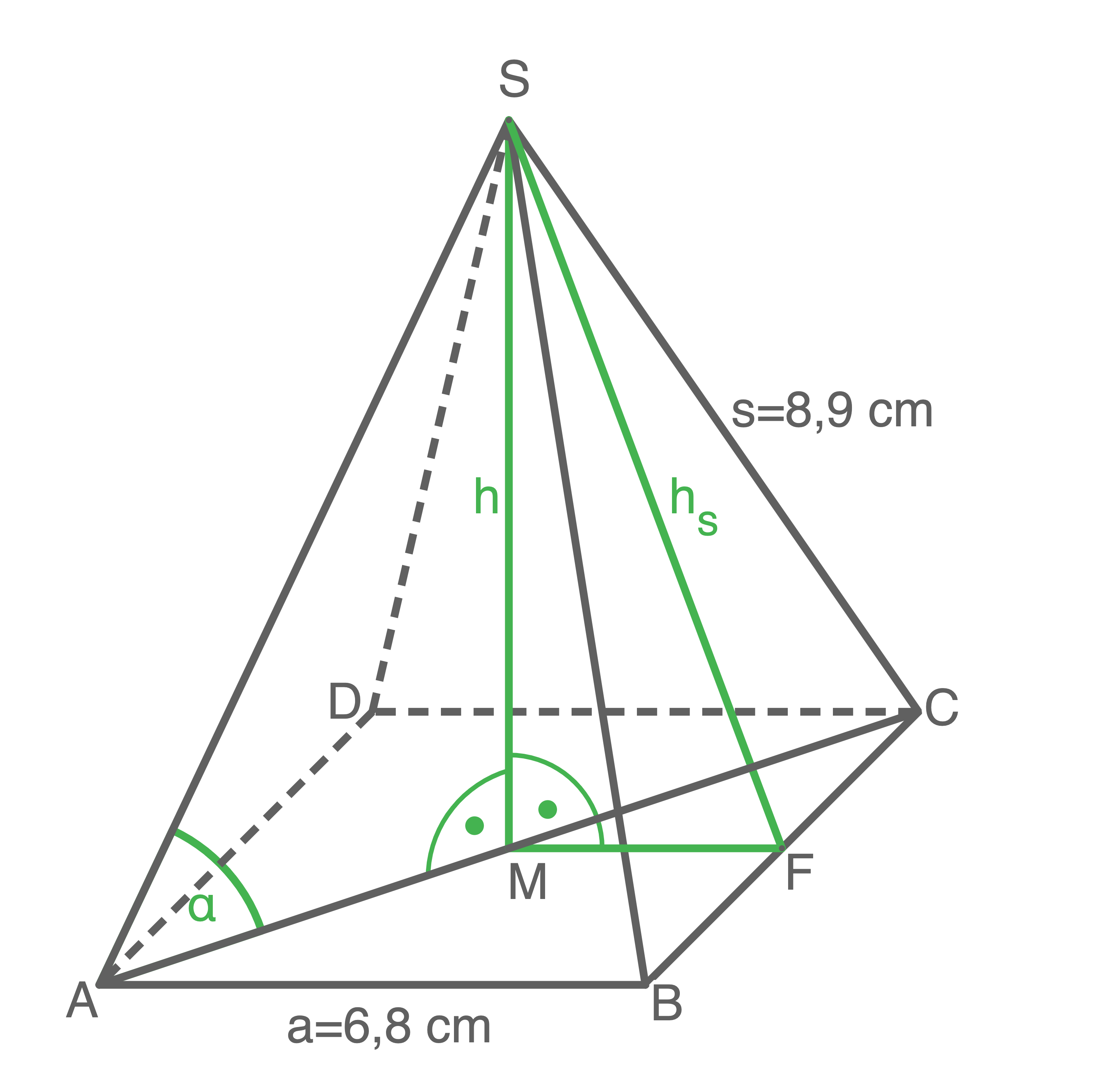
Gegeben ist eine quadratische Pyramide mit der Grundkante 
und der Seitenkante 
Berechnet werden soll die Höhe 
der Pyramide.
Dazu werden die zwei Hilfsdreiecke betrachtet:
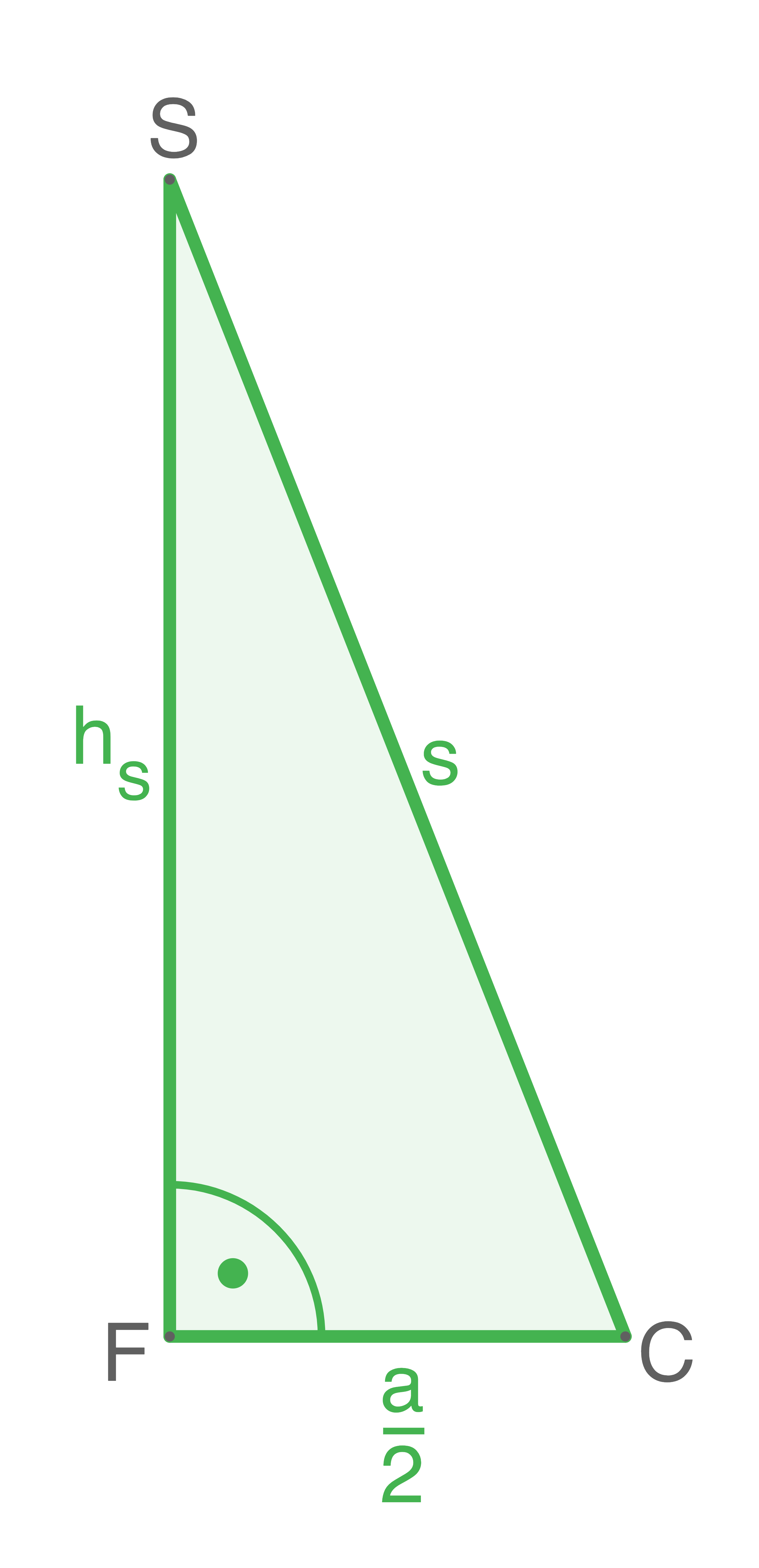
Hilfsdreieck 
Mit diesem Dreieck kann die Seite 
mit Hilfe der Seite 
und der halben Grundseite 
berechnet werden.
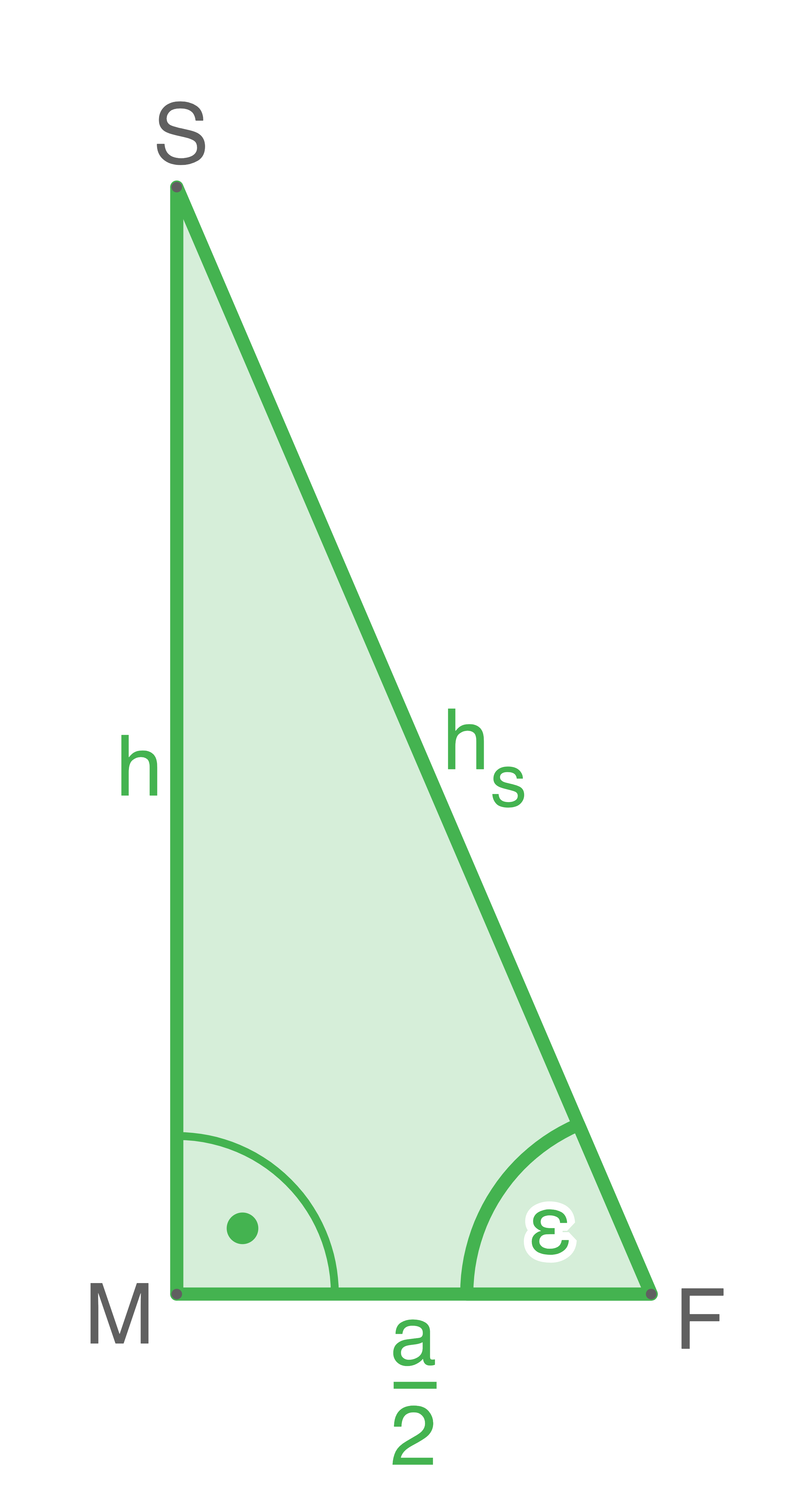
Hilfsdreieck 
Mit diesem Dreieck kann die Höhe mit Hilfe der Seite und der halben Grundseite berechnet werden.
1
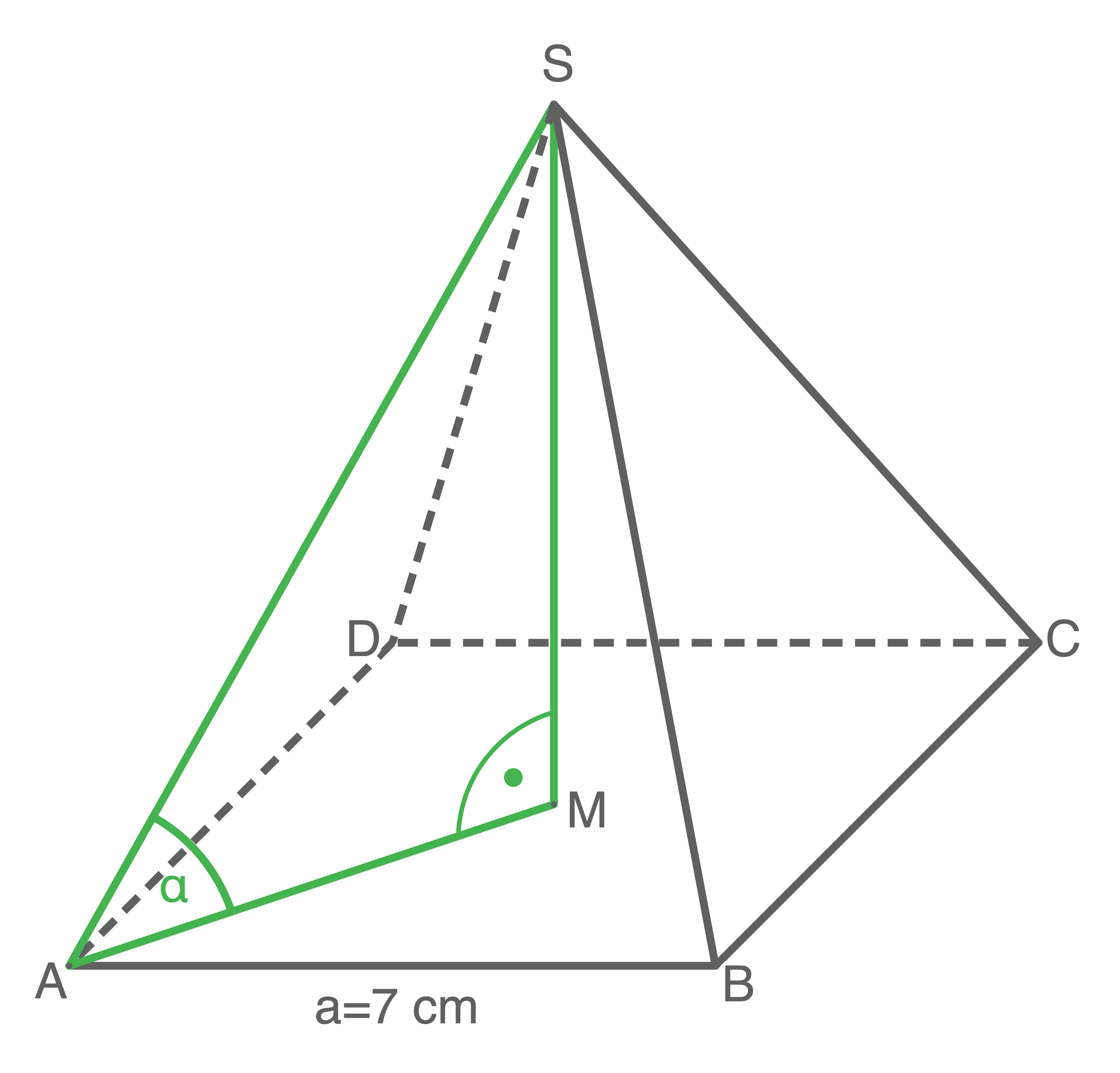
Gegeben ist eine quadratische Pyramide mit 
und 
a)
Berechne die Höhe der Pyramide.
b)
Berechne den Flächeninhalt des Dreiecks 
2
Gegeben ist eine quadratische Pyramide mit 
und 
a)
Berechne den Flächeninhalt des Dreiecks 
b)
Berechne die Größe des Winkels 
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
1. Schritt: Länge von 
berechnen
![\(\begin{array}[t]{rll}
\overline{AM}^2&=&\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2\quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
\overline{AM}&=&\sqrt{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2}\\[5pt]
&=&\sqrt{\left(\dfrac{7\,\text{cm}}{2}\right)^2+\left(\dfrac{7\,\text{cm}}{2}\right)^2}\\[5pt]
\overline{AM}&=& 4,9\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/cf3f7b4ef74ca19ffc8defd4b723e3e23f23956d3e575a406cd2e92c96e137c1?color=5a5a5a)
2. Schritt: Länge von 
berechnen
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{h}{\overline{AM}} \quad \scriptsize \mid\;\cdot \overline{AM} \\[5pt]
\tan(\alpha)\cdot \overline{AM}&=& h\\[5pt]
h&=&\tan(50^\circ)\cdot 4,9\,\text{cm}\\[5pt]
h&=& 5,8\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/a81542672ac950b0ef93c9892d5e59a136ea2f63e5134bbeb6bfd9b679f172bd?color=5a5a5a)
b)
2
a)
1. Schritt: Länge von berechnen
![\(\begin{array}[t]{rll}
h_s^2+\overline{FC}^2 &=& s^2 \quad \scriptsize \mid\; - \overline{FC}^2 \\[5pt]
h_s^2&=& s^2-\overline{FC}^2\quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
h_s&=&\sqrt{s^2-\overline{FC}^2}\\[5pt]
&=&\sqrt{(8,9\,\text{cm})^2-(3,4\,\text{cm})^2}\\[5pt]
h_s&=& 8,2\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/12b1ae816ae2fd1c88123f9e5f69c2288d4705e56cc752218c8115b148e88c0a?color=5a5a5a)
2. Schritt: Länge von berechnen
![\(\begin{array}[t]{rll}
h^2 + \overline{MF}^2 &=& h_s^2 \quad \scriptsize \mid\;-\overline{MF}^2 \\[5pt]
h^2&=& h_s^2-\overline{MF}^2\quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
h&=&\sqrt{h_s^2-\overline{MF}^2}\\[5pt]
&=&\sqrt{(8,2\,\text{cm})^2-(3,4\,\text{cm})^2}\\[5pt]
h&=& 7,5\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/a42c4b80904d757a45321c135ca43d211bbdef24d5badda732193550a3e677db?color=5a5a5a)
3. Schritt: Flächeninhalt von berechnen
![\(\begin{array}[t]{rll}
A_{MFS}&=&\dfrac{1}{2}\cdot \dfrac{a}{2}\cdot h \\[5pt]
&=&\dfrac{1}{2}\cdot 3,4\,\text{cm}\cdot 7,5\,\text{cm}\\[5pt]
A_{MFS}&=&12,8\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/32fd350347ebaec84fee1c5858c73da8e2307d0e18b5223a674d83783316a71d?color=5a5a5a)
b)