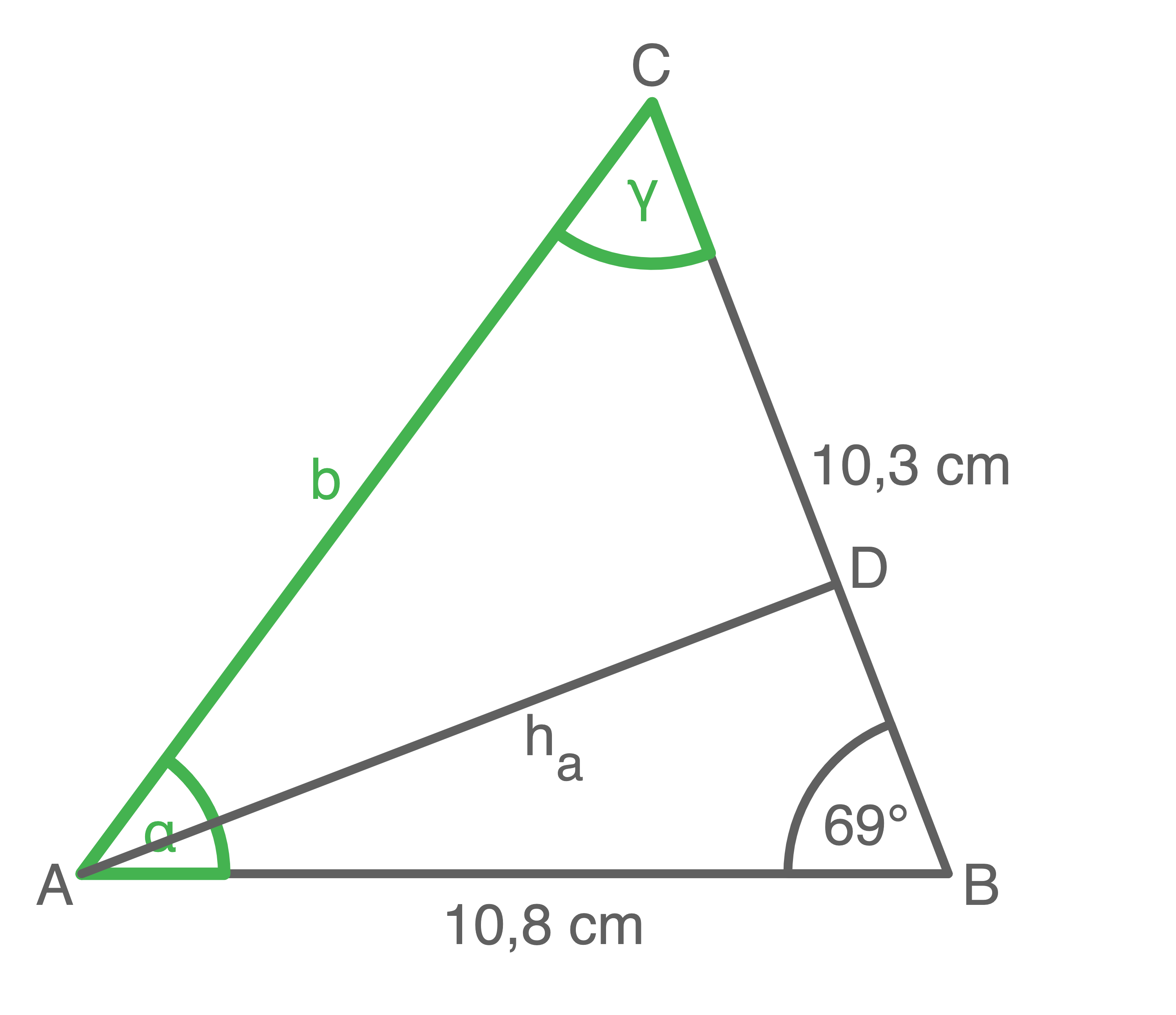
Allgemeines Dreieck
Um Berechnungen im allgemeinen Dreieck durchzuführen, wird das Dreieck in rechtwinklige Teildreiecke unterteilt.
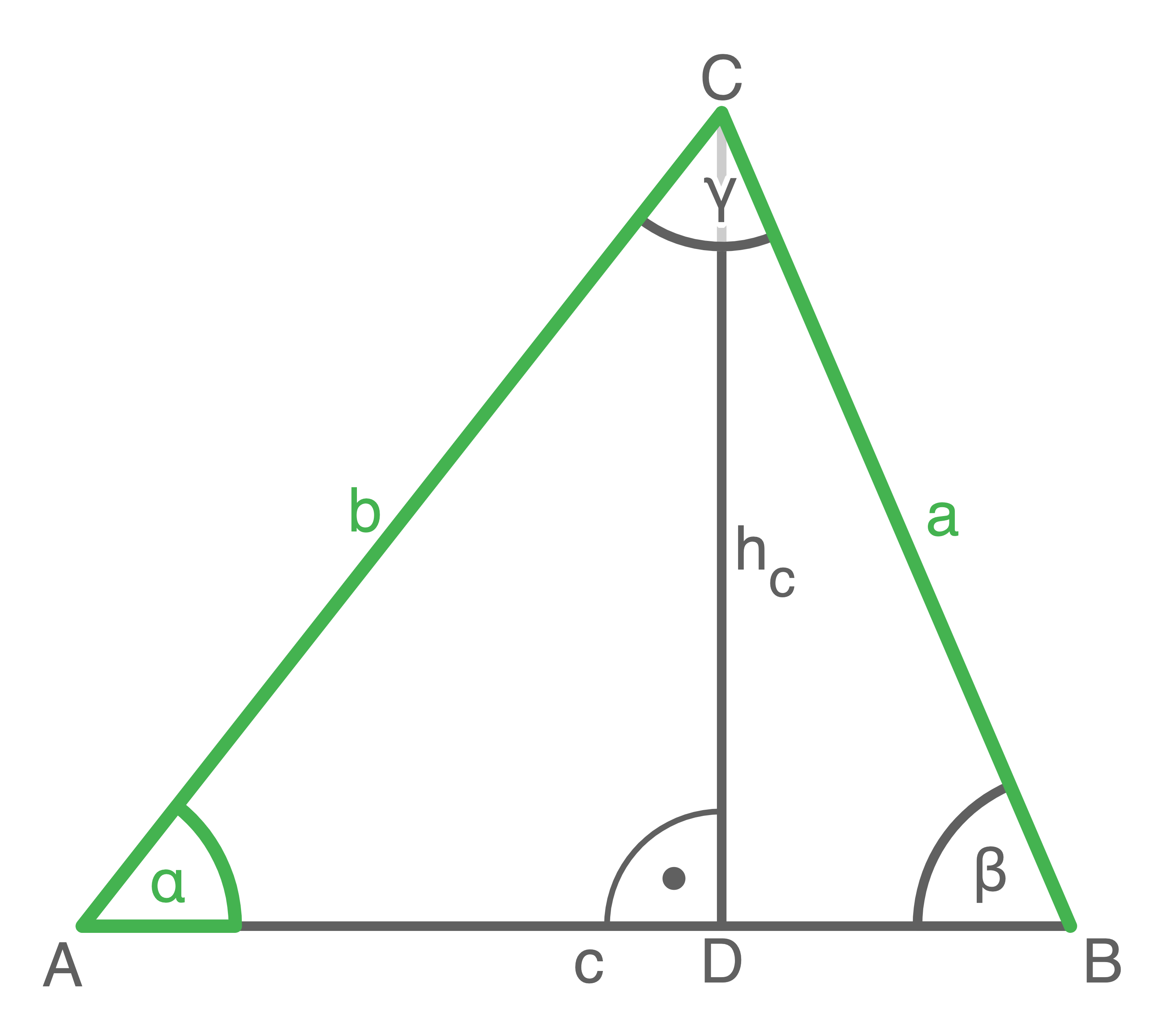 Größe von
Größe von  berechnen
berechnen
 berechnen
berechnen
 berechnen
berechnen


Beispiel
Im Dreieck  sind zwei Seiten und ein Winkel gegeben:
sind zwei Seiten und ein Winkel gegeben:

 und
und  Gesucht ist die Länge von
Gesucht ist die Länge von  und die Größe von
und die Größe von  Dazu wird das Dreieck
Dazu wird das Dreieck  durch
durch  in zwei Teildreiecke unterteilt.
in zwei Teildreiecke unterteilt.

1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{h_c}{b}\quad \scriptsize \mid\;\cdot b \\[5pt]
\sin(\alpha)\cdot b&=&h_c\\[5pt]
h_c&=&\sin(\alpha)\cdot b\\[5pt]
&=&\sin(52^\circ)\cdot 17,8\,\text{cm}\\[5pt]
h_c&=&14\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/294be061af8bcaa2ef353ad37fd11941c2fe83ad1a7e2dd15c0093ee5d3a14ed?color=5a5a5a)
2. Schritt: Größe von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=&\dfrac{h_c}{a} \\[5pt]
&=&\dfrac{14\,\text{cm}}{15,2\,\text{cm}} \\[5pt]
\sin(\beta)&=&0,9 \\[5pt]
\beta&=&64,2^\circ
\end{array}\)](https://mathjax.schullv.de/95b5efcb9c48a865a6c55c1b2490d84c6ec1bcebb52da6b491ef4d9e676c457c?color=5a5a5a)
Länge von
1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
(\overline{AD})^2+h_c^2&=&b^2\quad \scriptsize \mid\;-h_c^2 \\[5pt]
(\overline{AD})^2&=&b^2-h_c^2\quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
\overline{AD}&=&\sqrt{b^2-h_c^2}\\[5pt]
&=&\sqrt{(17,8\,\text{cm})^2-(14\,\text{cm})^2}\\[5pt]
\overline{AD}&=&11\,\text{cm}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/3dc5fcbe00d03269915149e6859193fd12e4729ddb951cc3af538b5b7965d8c8?color=5a5a5a)
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
(\overline{DB})^2+h_c^2&=&a^2\quad \scriptsize \mid\;-h_c^2 \\[5pt]
(\overline{DB})^2&=&a^2-h_c^2\quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
\overline{DB}&=&\sqrt{a^2-h_c^2}\\[5pt]
&=&\sqrt{(15,2\,\text{cm})^2-(14\,\text{cm})^2}\\[5pt]
\overline{DB}&=&5,9\,\text{cm}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/ee51927449a4e4265fe05cc920562962cd8222640962e7f40dfa6c5569c83793?color=5a5a5a)
3. Schritt: Länge von
1
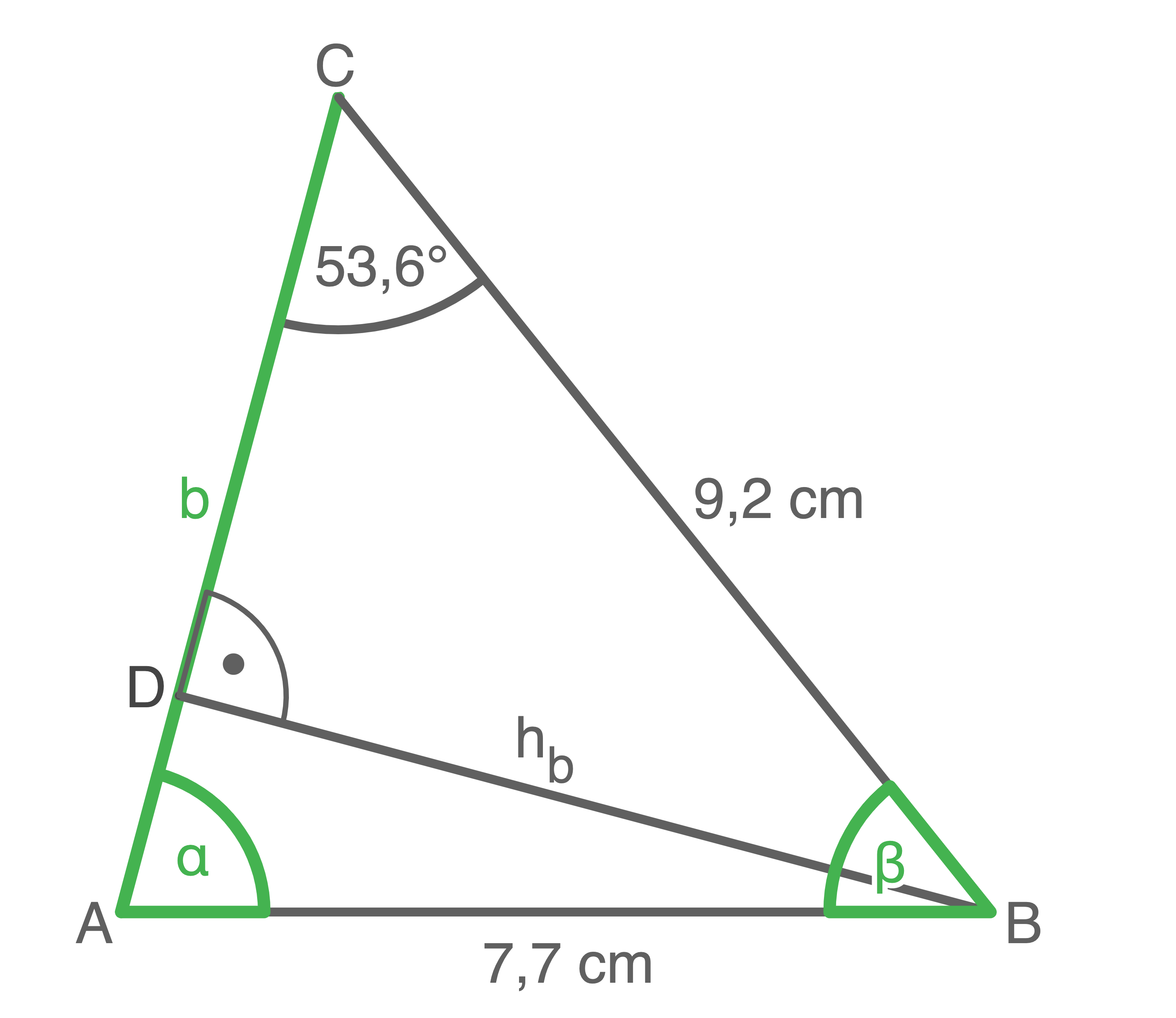
Das Dreieck kann wie dargestelt geteilt werden. Berechne die fehlenden Größen.
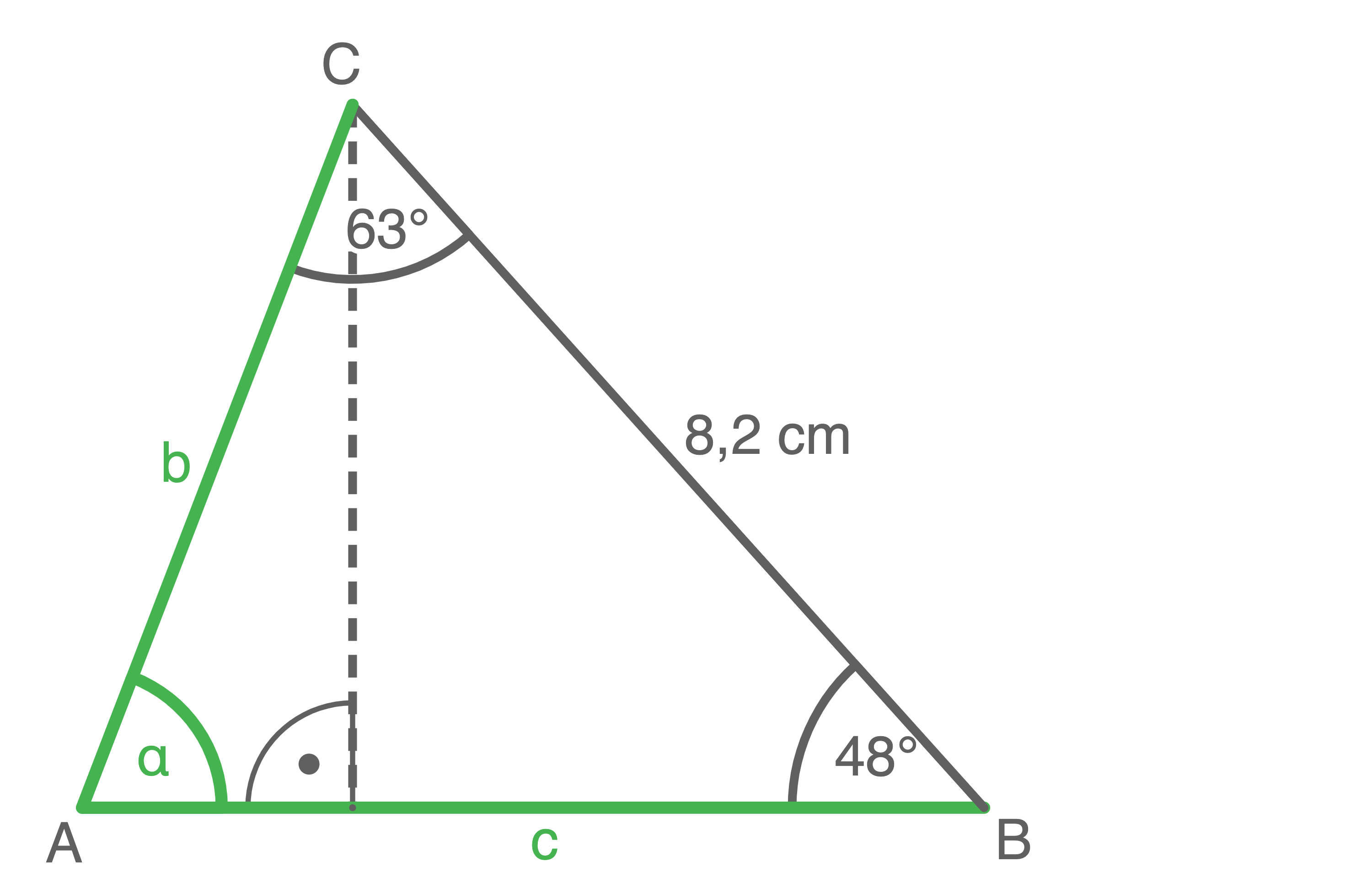
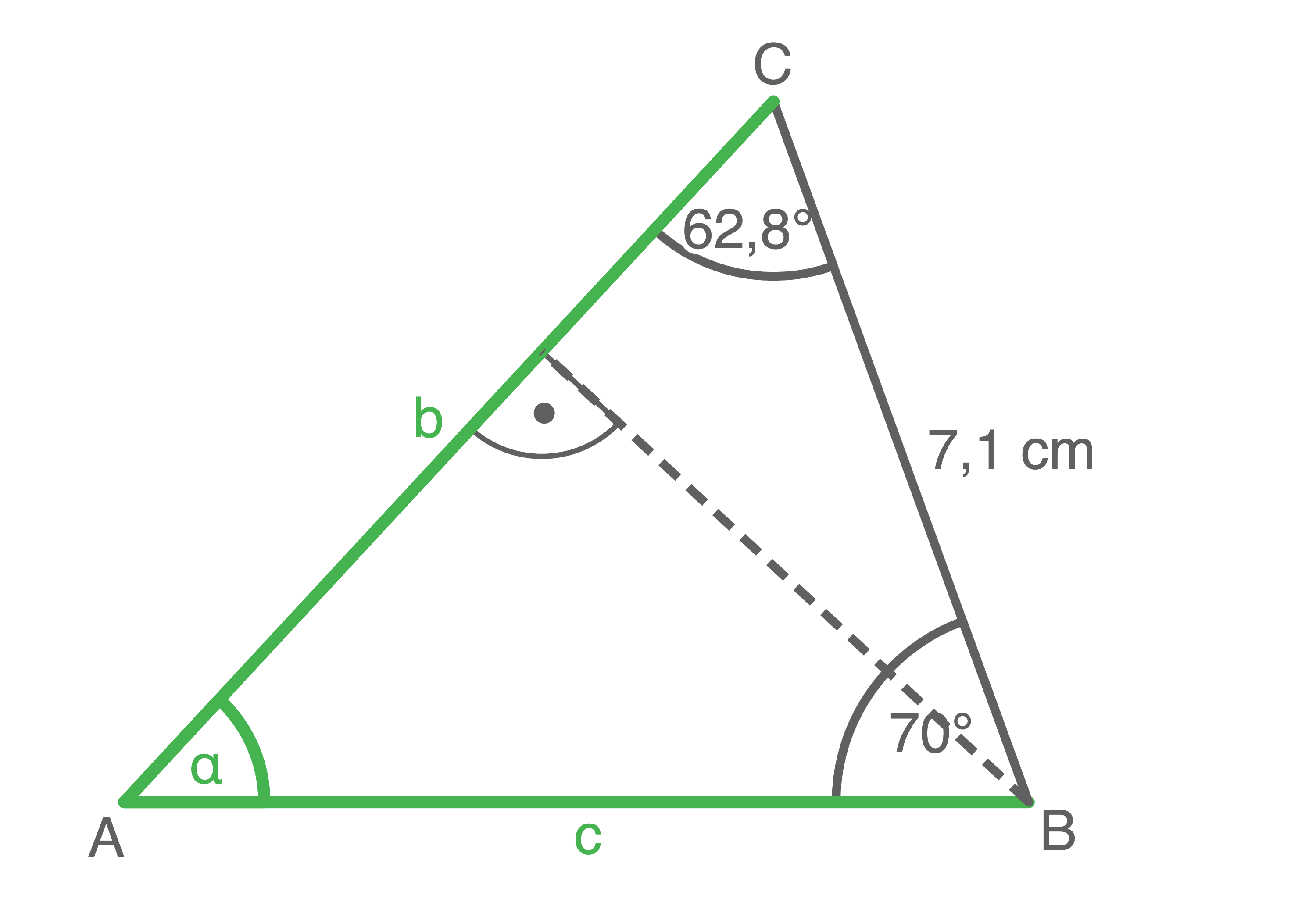
a)

b)

2
Berechne die fehlenden Größen und unterteile dafür das Dreieck mit einer geeigneten Höhe.
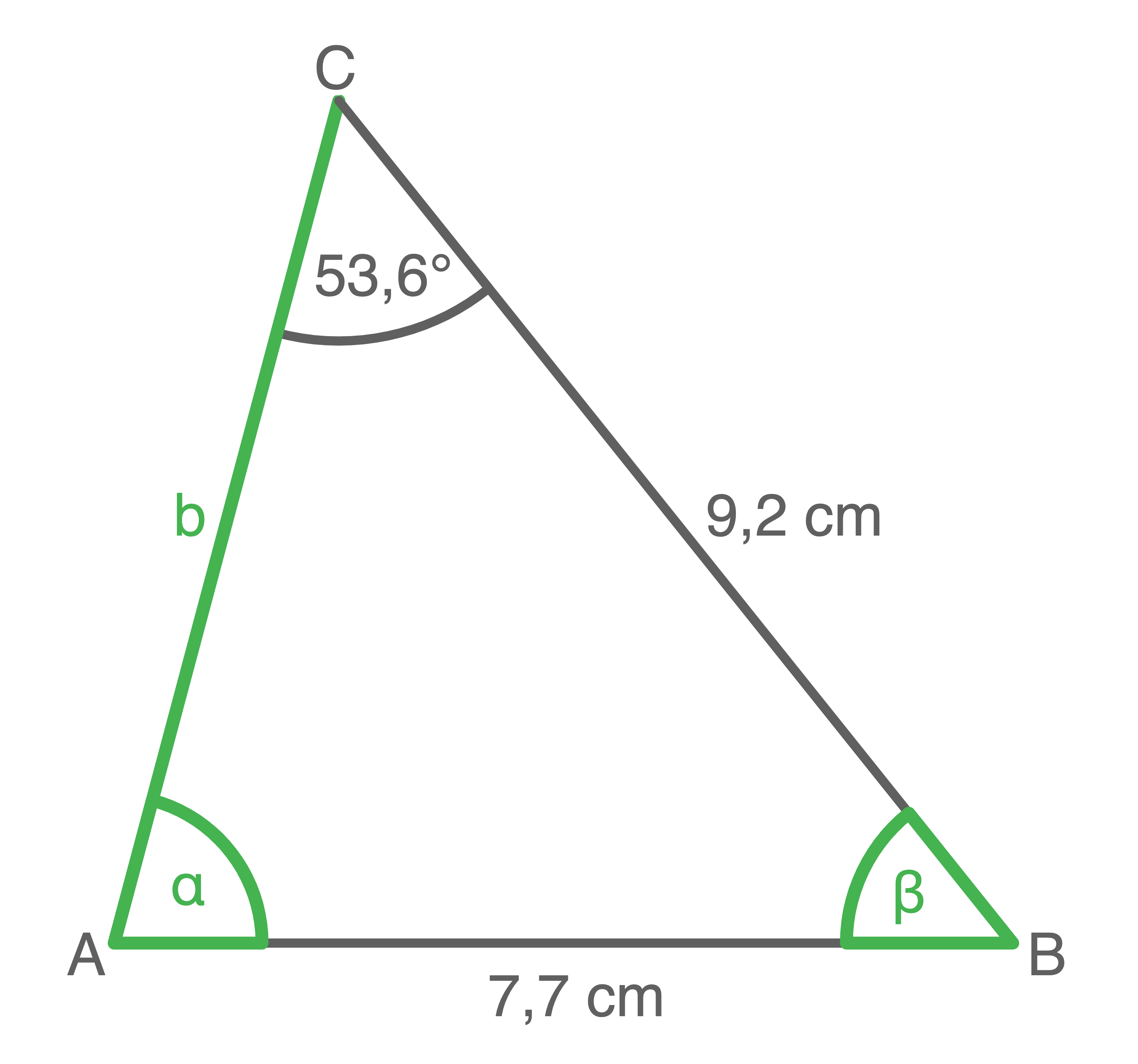
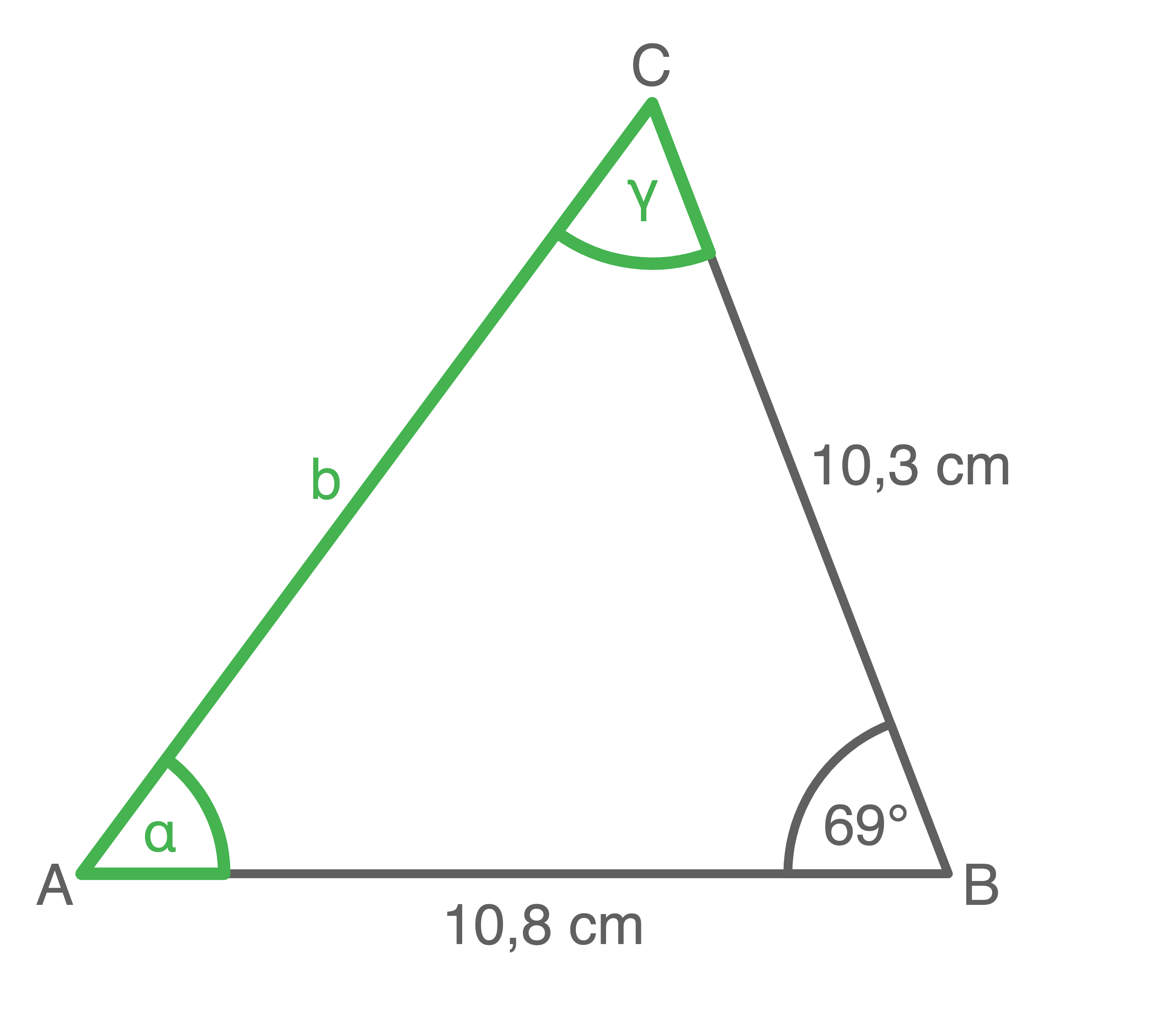
a)

b)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
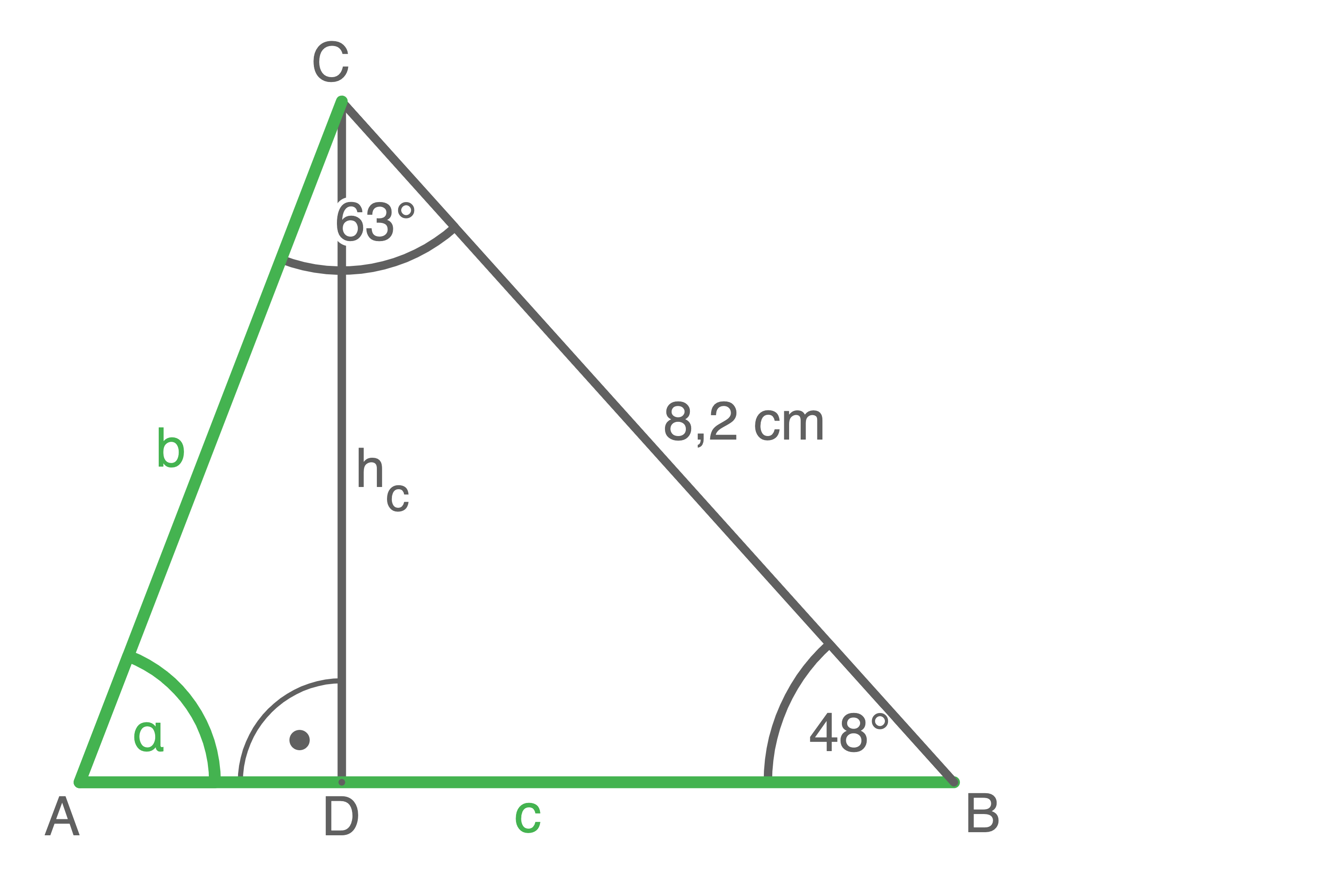
b)
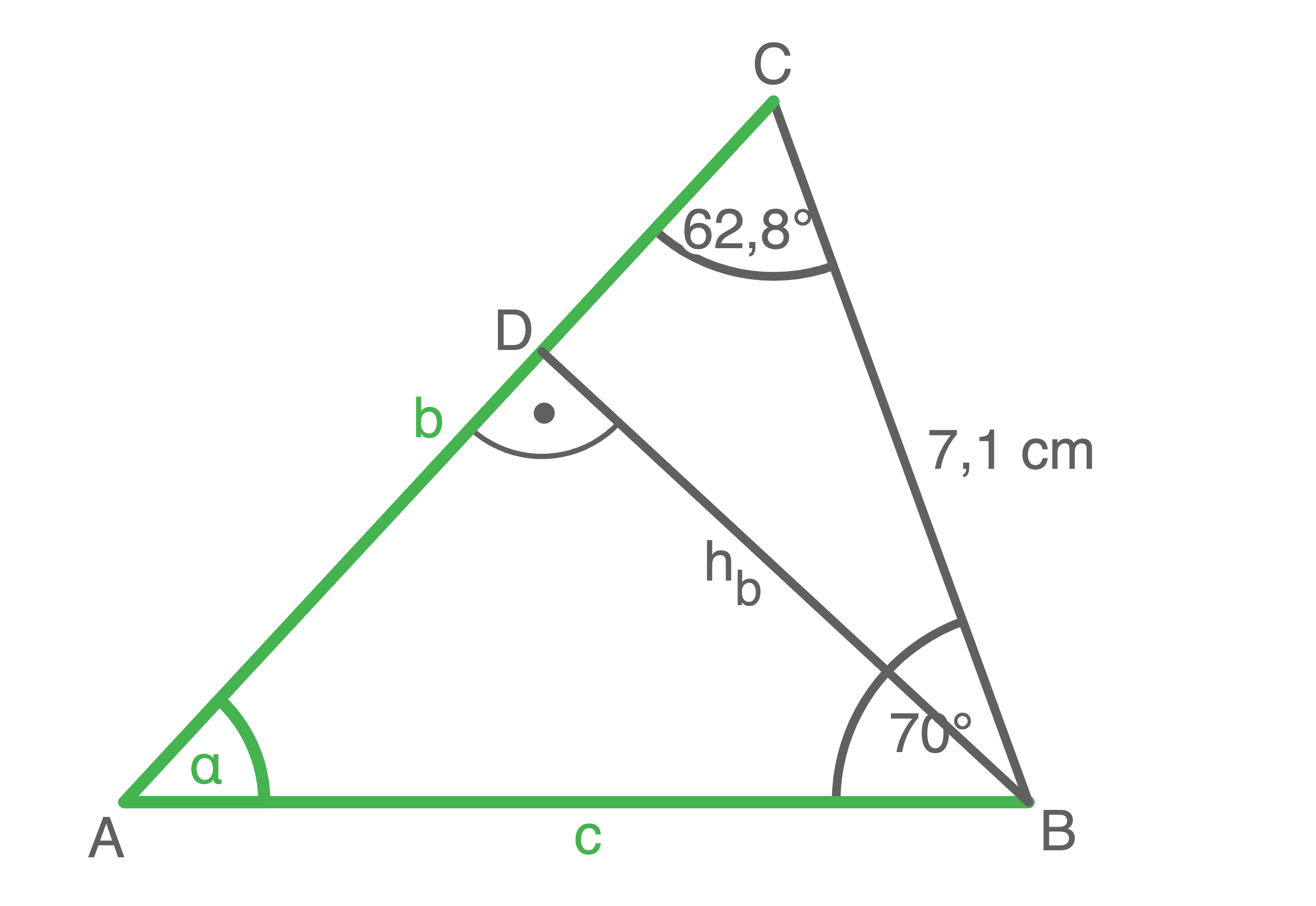
2
a)
b)