Quadratische Funktionen mit Koeffizient
Das Schaubild der quadratischen Funktion  ist eine Parabel, die um den Summanden
ist eine Parabel, die um den Summanden  verschoben ist. Der Scheitelpunkt hat dabei die Koordinaten
verschoben ist. Der Scheitelpunkt hat dabei die Koordinaten  Die Parabel wird um den Koeffizienten
Die Parabel wird um den Koeffizienten  gestreckt oder gestaucht. Außerdem bestimmt der Koeffizient
gestreckt oder gestaucht. Außerdem bestimmt der Koeffizient  ob die Parabel nach oben oder nach unten geöffnet ist.
Für die Öffnung der Parabel gilt:
ob die Parabel nach oben oder nach unten geöffnet ist.
Für die Öffnung der Parabel gilt:
- Wenn
dann ist die Parabel nach oben geöffnet.
- Wenn
dann ist die Parabel nach unten geöffnet.
- Für
ist die Parabel breiter als die Normalparabel.
- Für
ist die Parabel schmaler als die Normalparabel.
1
Beschreibe die Öffung und Form der Parabel im Verlgeich zu einer Normalparabel und zeichne den Graph der Funktion.




a)
b)
c)
d)
2
Ordne den Funktionsgleichungen die Graphen zu und begründe deine Entscheidung.
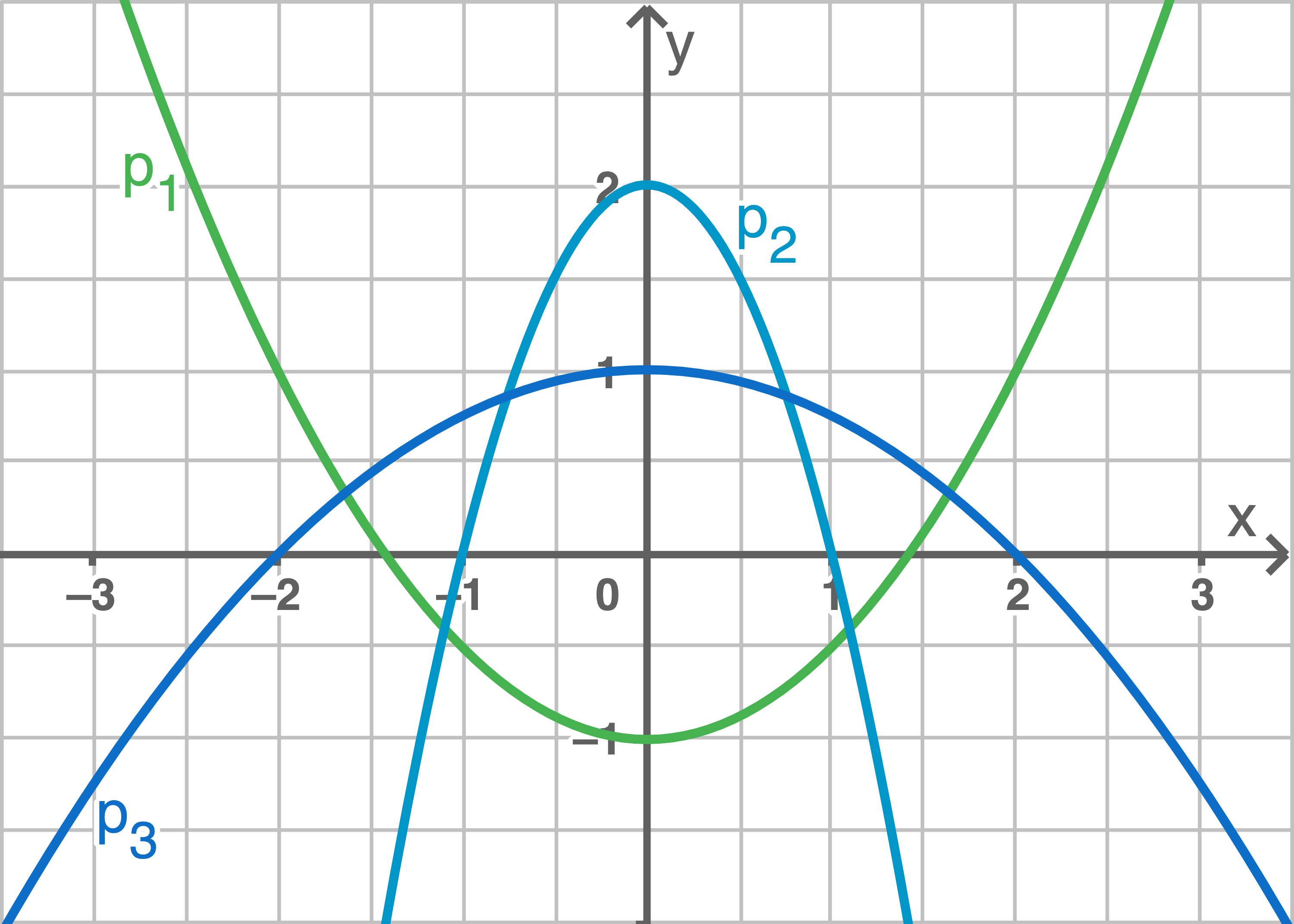

3
Bestimme den Veschiebungsfaktor  sowie den Koeffizienten
sowie den Koeffizienten  durch Ablesen aus dem Schaubild.
durch Ablesen aus dem Schaubild.
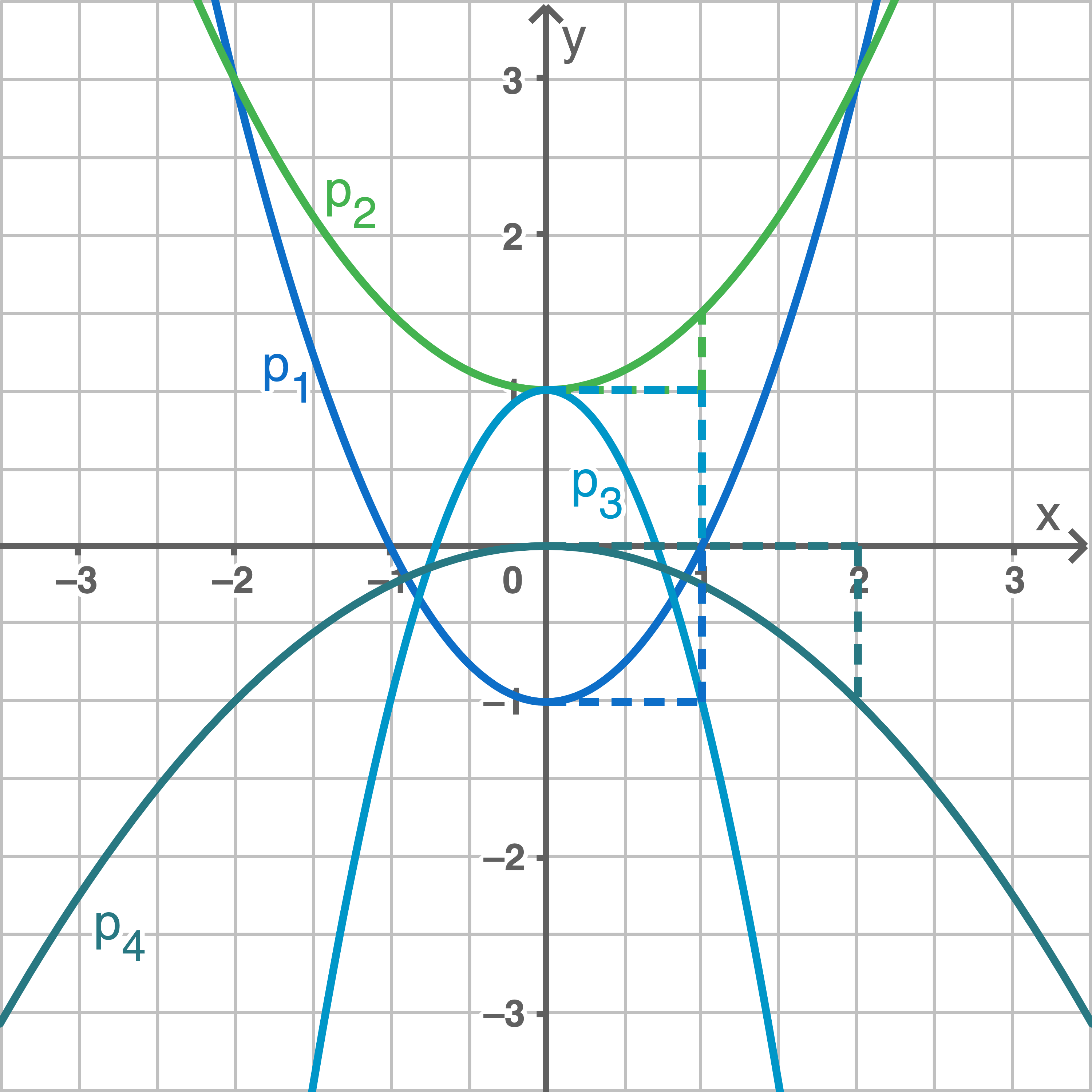

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
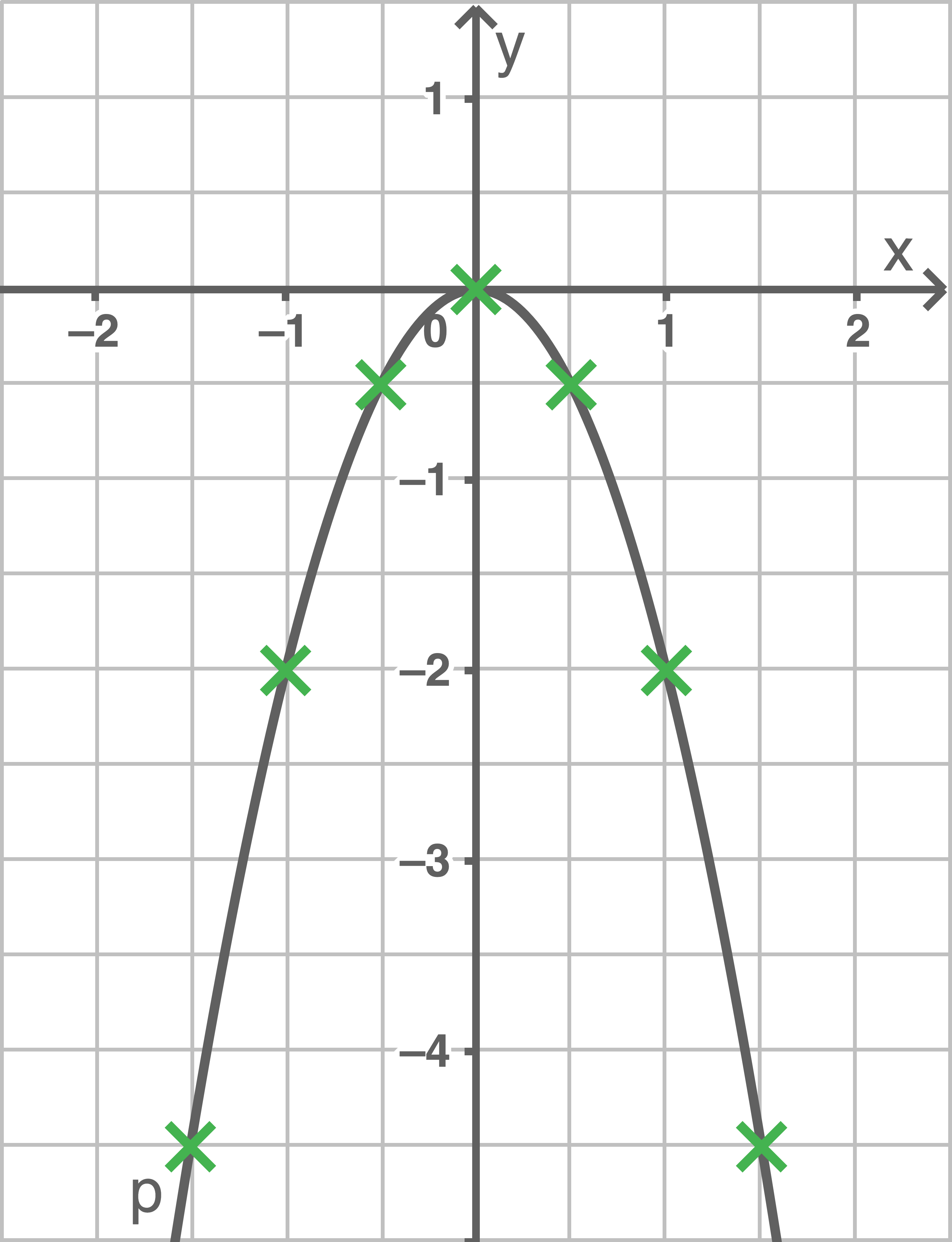
b)
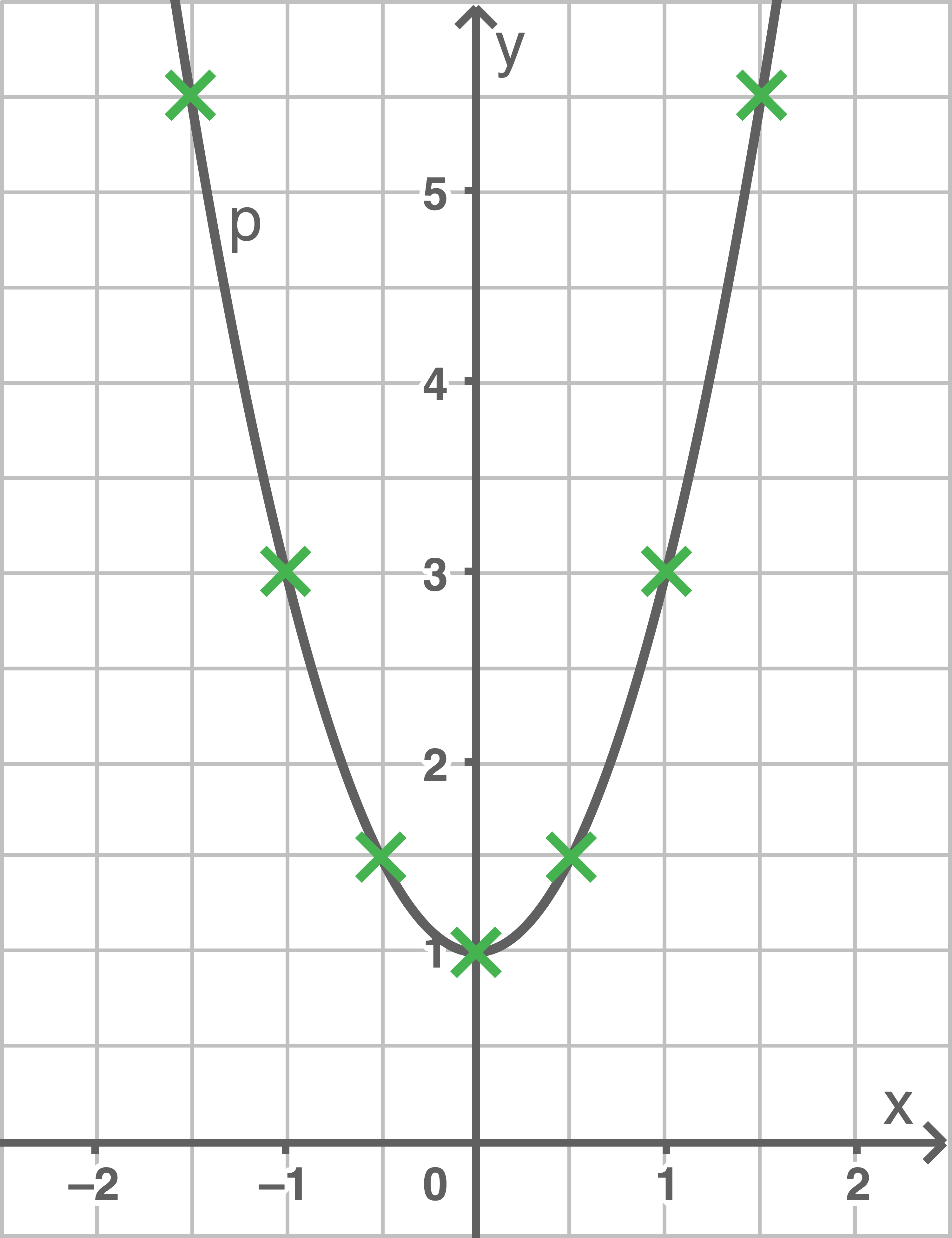
c)
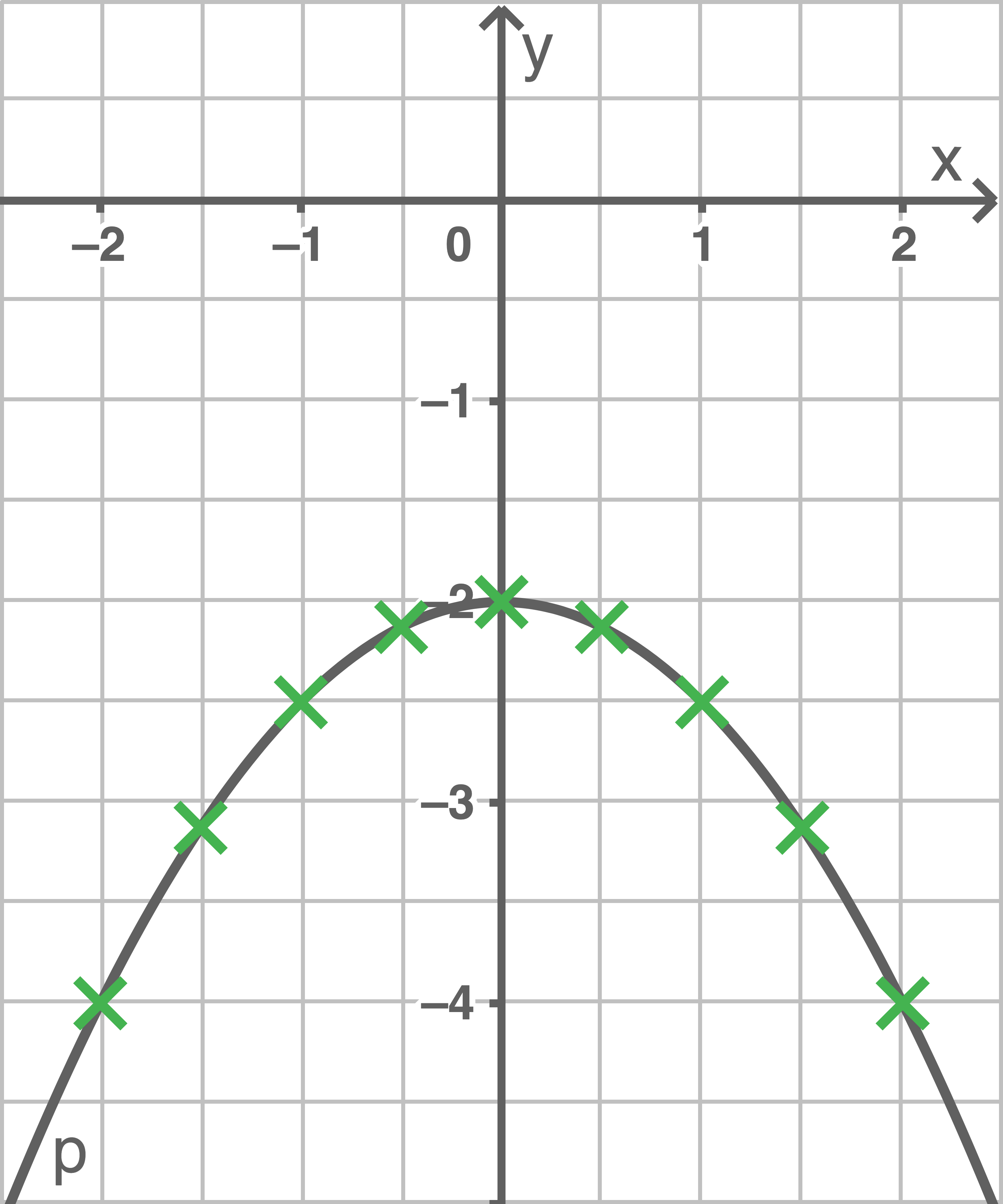
d)
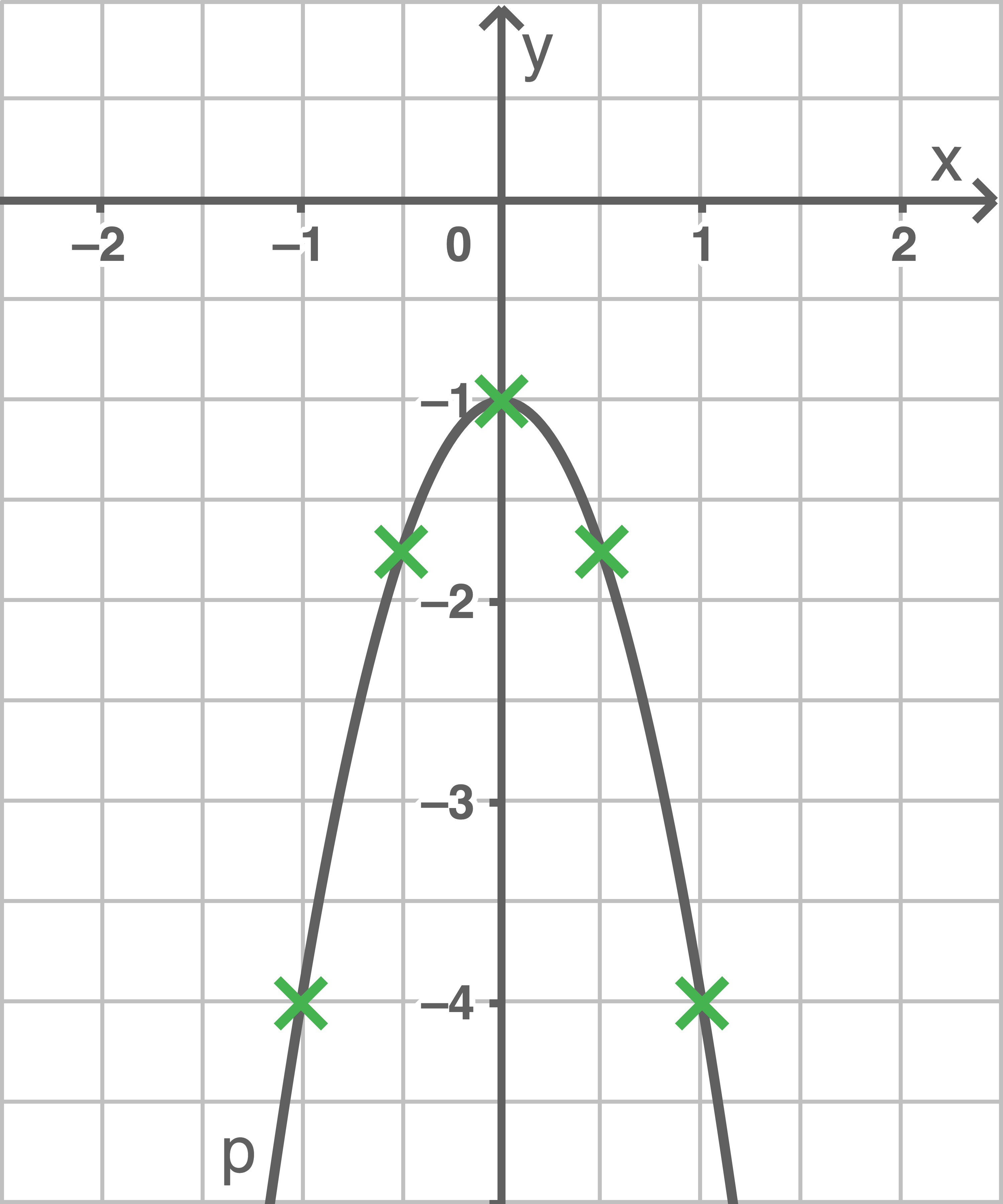
2
Funktionsgleichung  Der Verschiebungsfaktor ist
Der Verschiebungsfaktor ist  und der Koeffizient ist
und der Koeffizient ist  Da lediglich
Da lediglich  durch den Punkt
durch den Punkt  verläuft, ist das der passende Graph dazu.
Funktionsgleichung
verläuft, ist das der passende Graph dazu.
Funktionsgleichung  Der Verschiebungsfaktor ist
Der Verschiebungsfaktor ist  und der Koeffizient ist
und der Koeffizient ist  Da lediglich
Da lediglich  durch den Punkt
durch den Punkt  verläuft, ist das der passende Graph dazu.
Funktionsgleichung
verläuft, ist das der passende Graph dazu.
Funktionsgleichung  Der Verschiebungsfaktor ist
Der Verschiebungsfaktor ist  und der Koeffizient ist
und der Koeffizient ist  Da lediglich
Da lediglich  durch den Punkt
durch den Punkt  verläuft, ist das der passende Graph dazu.
verläuft, ist das der passende Graph dazu.
3
Parabel 

 Es gilt also:
Es gilt also:  Parabel
Parabel 

 Es gilt also:
Es gilt also:  Parabel
Parabel 

 Es gilt also:
Es gilt also:  Parabel
Parabel 

 Es gilt also:
Es gilt also: 