Erwartungswert

Für Betreiber*innen und Spieler*innen eines Glücksspiels ist es interessant zu wissen, wie hoch der durchschnittliche Gewinn oder Verlust eines Spiels ist.

Um das zu herauszufinden, wird der Erwartungswert $E$ berechnet:

$\begin{array}[t]{rll} E&=&G_1\cdot P(G_1)+G_2\cdot P(G_2)+ ... \\[5pt] && ...+G_n\cdot P(G_n)-\text{Einsatz} \end{array}$

$G_1,$ $G_2,$ $...$ $, G_n$ sind die verschiedenen Gewinne.

Dabei gilt:

$E=0 \Rightarrow$ Es handelt sich um ein faires Spiel.
$E\gt0 \Rightarrow$ Die Spieler*innen machen durchnittlich Gewinn, die Betreiber*innen machen durchnittlich Verlust.
$E\lt0 \Rightarrow$ Die Spieler*innen machen durchnittlich Verlust, die Betreiber*innen machen durchnittlich Gewinn.

Beispiel

Das nebenstehende Glücksrad wird für ein Glücksspiel eingesetzt.

Zeigt das Glücksrad auf das grüne Feld, gewinnt der Spieler 15 €, bei dem blauen Feld gibt es 5 €. Bei allen anderen Feldern gibt es keinen Gewinn.

Der Spieleinsatz beträgt 2 €.

	$G$	$P(G)$
Grünes Feld	$15\,€$	$\dfrac{1}{6}$
Blaues Feld	$5\,€$	$\dfrac{1}{6}$
Sonstige Felder	$0\,€$	$\dfrac{4}{6}$

Mithilfe der obenstehenden Formel lässt sich der Erwartungswert berechnen:

$\begin{array}[t]{rll} E&=& 15\,€\cdot\dfrac{1}{6}+5\,€\cdot \dfrac{1}{6}+0\,€\cdot \dfrac{4}{6}-2\,€ \\[5pt] E&=& \dfrac{4}{3}\,€ \\[5pt] E&=& 1,33\,€ \\[5pt] \end{array}$

Im Schnitt macht man als Spieler*in pro Spiel $1,33\,€$ Gewinn.

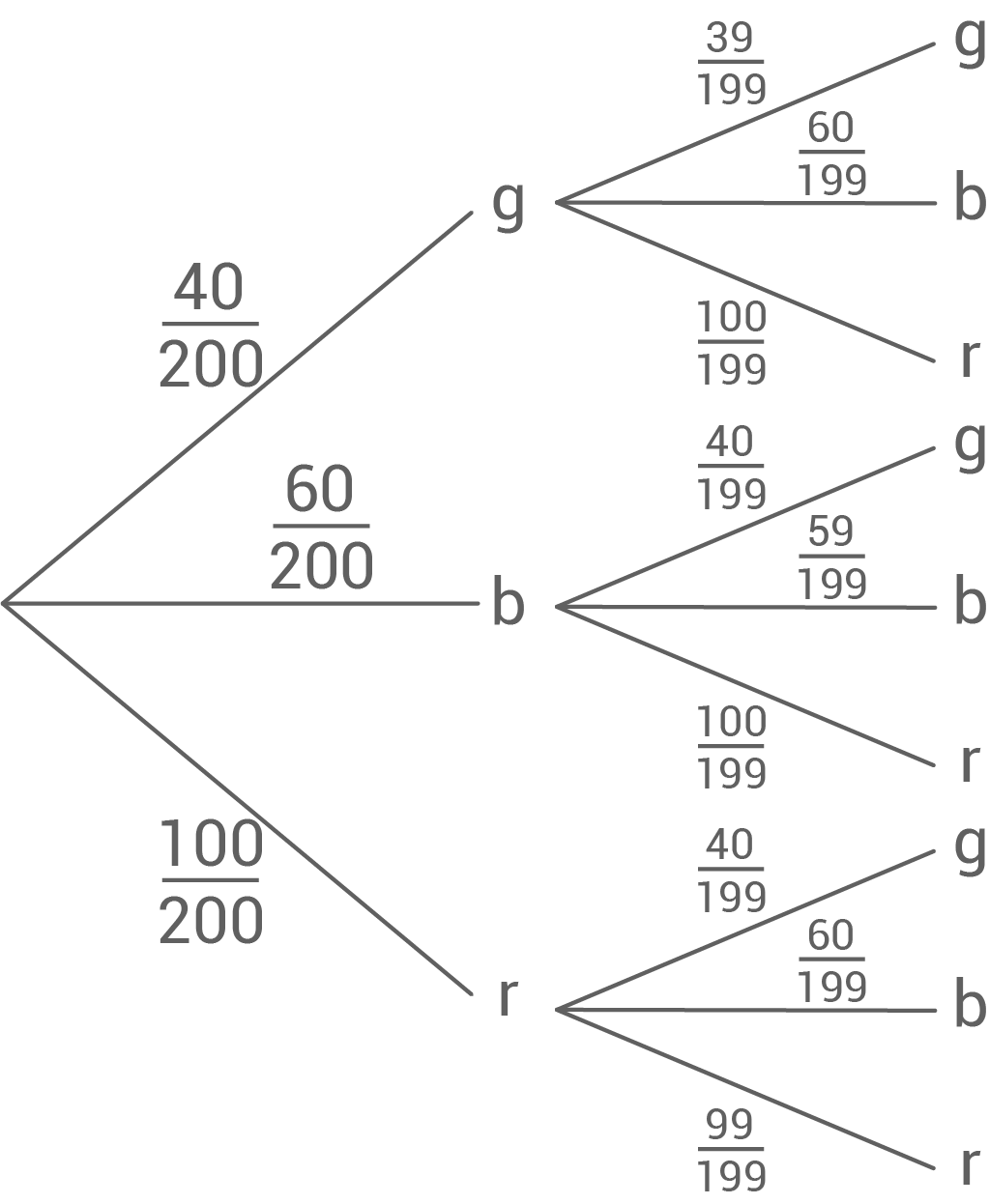
Auf einem Jahrmarkt wird ein Glücksspiel mit einer Lostrommel veranstaltet.
Es gibt insgesamt 200 Lose: 40 gelbe, 60 blaue und 100 rote Lose.

Es werden zwei Lose ohne Zurücklegen gezogen.

Wie groß ist die Wahrscheinlichkeit, zwei gleichfarbige Lose zu ziehen?

Der Betreiber verwendet den folgenden Gewinnplan.

Ereignis	Gewinn
Zwei gleichfarbige Lose	14,00 €
Ein blaues und rotes Los	9,00 €
Einsatz: 4,00 € pro Spiel

Wie viel Gewinn bzw. Verlust macht der Spieler im Durchschnitt pro Los?

Wie viel Gewinn bzw. Verlust macht der Betreiber im Durchschnitt pro Los?

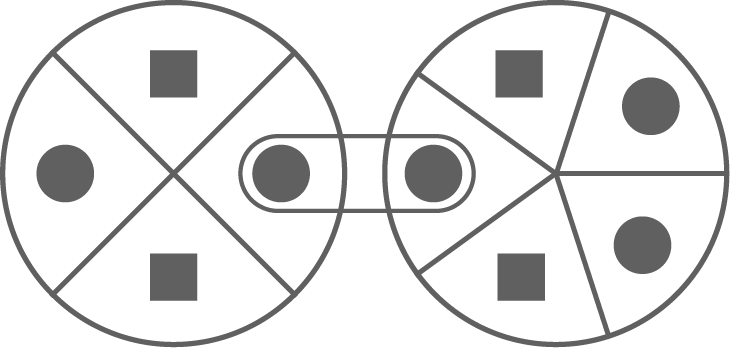
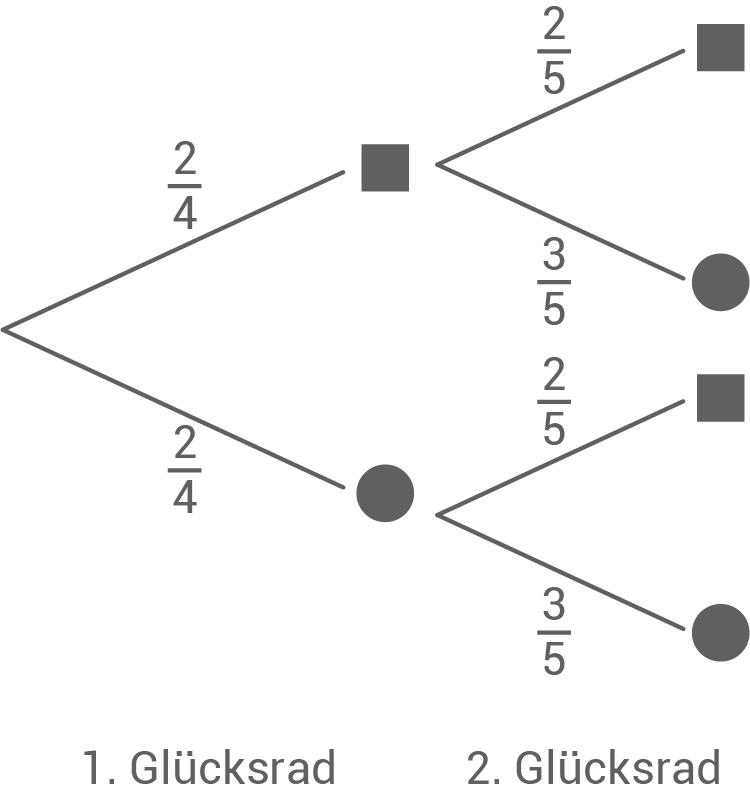
Die beiden Glücksräder werden gedreht.

Wenn sie stehen bleiben, erkennt man im Sichtfenster zwei Formen.
In der Abbildung sieht man im Sichtfenster zwei Kreise.

Mit welcher Wahrscheinlichkeit sind im Sichtfenster zwei Quadrate zu sehen?

Jule möchte daraus ein faires Glücksspiel machen.

Sie überlegt sich folgenden Gewinnplan:

Ereignis	Gewinn
Zwei Quadrate	7,00 €
Zwei Kreise	6,50 €
Ein Quadrat und ein Kreis	1,50 €
Einsatz: ? € pro Spiel

Wie hoch muss der Einsatz sein, damit Jule ein faires Glücksspiel hat?

Jules Bruder übernimmt den berechneten Einsatz für ein faires Spiel. Allerdings möchte er im Durchschnitt pro Spiel einen Gewinn von 1,00 € machen.

Wie muss der Gewinn für das Ereignis „Zwei Quadrate“ verändert werden, damit Jules Bruder im Durchschnitt pro Spiel einen Gewinn von 1,00 € macht?

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\quad P(\text{gleichfarbige Lose})$

$\begin{array}[t]{rll} &=&P(\text{g, g})+P(\text{b, b})+P(\text{r, r}) \\[5pt] &=& \dfrac{40}{200}\cdot \dfrac{39}{199}+\dfrac{60}{200}\cdot \dfrac{59}{199}+\dfrac{100}{200}\cdot \dfrac{99}{199} \\[5pt] &=& \dfrac{75}{199} \\[5pt] &=& 38\,\% \end{array}$

1. Schritt: Wahrscheinlichkeit berechnen, ein blaues und ein rotes Los zu ziehen

$\quad P(\text{blaues und rotes Los})$

$\begin{array}[t]{rll} &=&P(\text{b, r})+P(\text{r, b}) \\[5pt] &=& \dfrac{60}{200}\cdot \dfrac{100}{199}+\dfrac{100}{200}\cdot \dfrac{60}{199} \\[5pt] &=& \dfrac{60}{199}\\[5pt] &=& 30\,\%\\[5pt] \end{array}$

2. Schritt: Tabelle erstellen

	$G$	$P(G)$
Gleichfarbige Lose	$9\,€$	$\dfrac{75}{199}$
Gelbes und blaues Los	$14\,€$	$\dfrac{60}{199}$

3. Schritt: Erwartungswert berechnen

$\begin{array}[t]{rll} E&=&G_1\cdot P(G_1)+G_2\cdot P(G_2)-\text{Einsatz} \\[5pt] E&=& 9\,€\cdot \dfrac{75}{199}+14\,€\cdot \dfrac{60}{199}-4,00\,€ \\[5pt] E&=& 3,61\,€ \\[5pt] \end{array}$

Der Spieler macht im Durchschnitt pro Los 3,61 € Gewinn.
Der Betreiber macht im Durchschnitt pro Los 3,61 € Verlust.

$\begin{array}[t]{rll} P(\text{Zwei Quadrate})&=&\dfrac{2}{4}\cdot \dfrac{2}{5} \\[5pt] &=&\dfrac{1}{5} \\[5pt] &=&20\,\% \\[5pt] \end{array}$

1. Schritt: Wahrscheinlichkeit berechnen, zwei Kreise im Sichtfenster zu sehen

$\begin{array}[t]{rll} P(\text{Zwei Kreise})&=&\dfrac{2}{4}\cdot \dfrac{3}{5} \\[5pt] &=& \dfrac{3}{10}\\[5pt] &=& 30\,\%\\[5pt] \end{array}$

2. Schritt: Wahrscheinlichkeit berechnen, ein Kreis und ein Quadrat im Sichtfenster zu sehen

$\begin{array}[t]{rll} P(\text{Kreis und Quadrat})&=&\dfrac{2}{4}\cdot \dfrac{3}{5}+\dfrac{2}{4}\cdot \dfrac{2}{5} \\[5pt] &=&\dfrac{1}{2} \\[5pt] &=& 50\,\%\\[5pt] \end{array}$

3. Schritt: Tabelle erstellen

	$G$	$P(G)$
Zwei Quadrate	$7,00\,€$	$\dfrac{1}{5}$
Zwei Kreise	$6,50\,€$	$\dfrac{3}{10}$
Ein Quadrat und ein Kreis	$1,50\,€$	$\dfrac{1}{2}$

4. Schritt: Einsatz berechnen

Rechenweg anzeigen

$x = 4,10\,€$

Jule muss einen Einsatz von 4,10 € verlangen, damit das Glücksspiel fair ist.

Rechenweg anzeigen

$G_1= 2,00\,€$

Damit Jules Bruder im Durchschnitt pro Spiel einen Gewinn von 1,00 € macht, muss der Gewinn für das Ereignis „Zwei Quadrate“ auf 2,00 € reduziert werden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?