Einheitskreis und Sinusfunktion
Die Sinusfunktion ordnet jedem Winkel eine Streckenlänge zu.
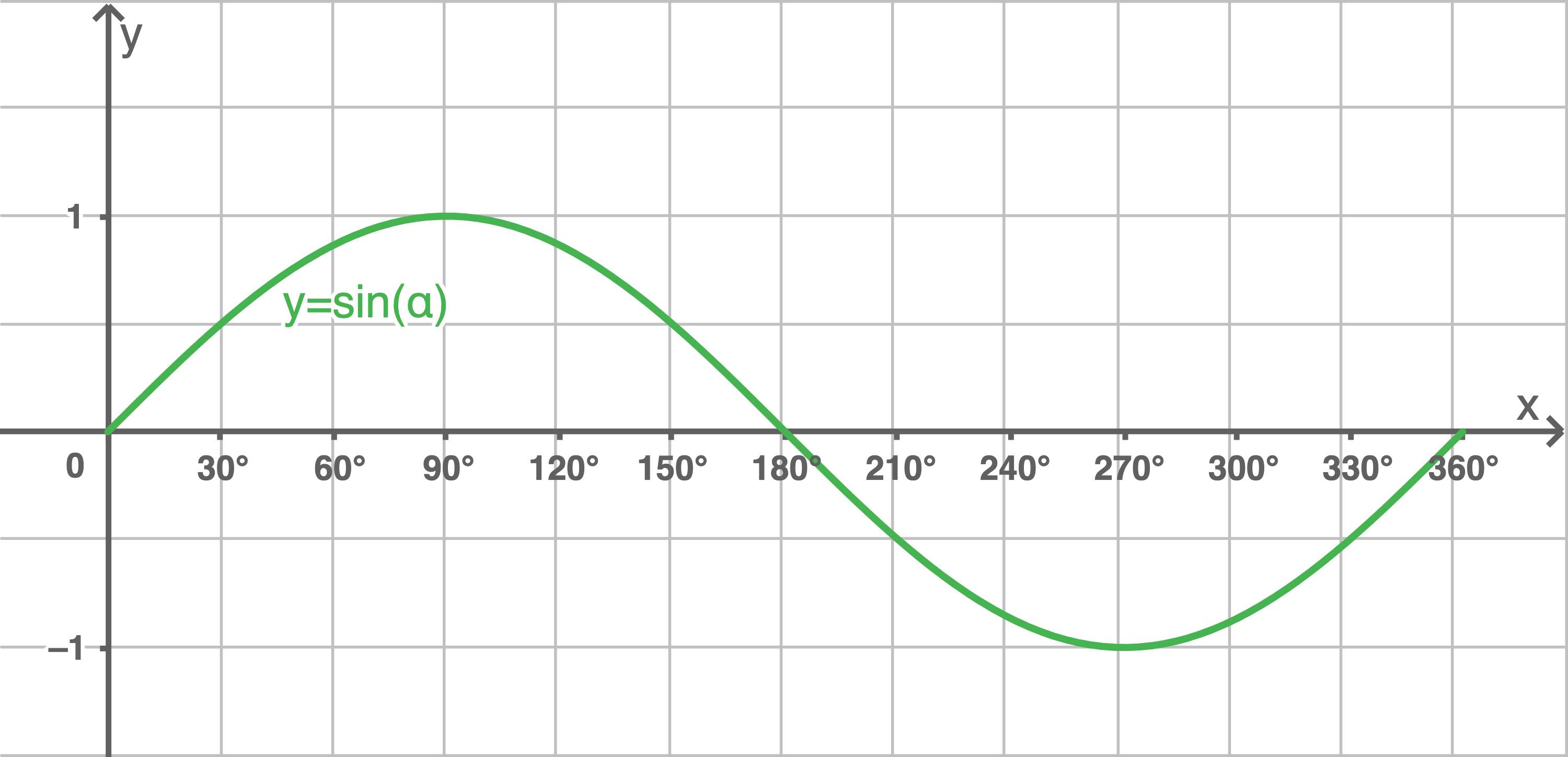
Die Sinusfunktion ist eine trigonometrische Funktion und ihr Graph heißt Sinuskurve.
 In einem rechtwinkligen Dreieck, bei dem die Hypotenuse eine Länge von 1 LE hat, gilt z.B.:
In einem rechtwinkligen Dreieck, bei dem die Hypotenuse eine Länge von 1 LE hat, gilt z.B.:
 im rechtwinkligen Dreieck ein Sinuswert zuordnen lässt.
im rechtwinkligen Dreieck ein Sinuswert zuordnen lässt.
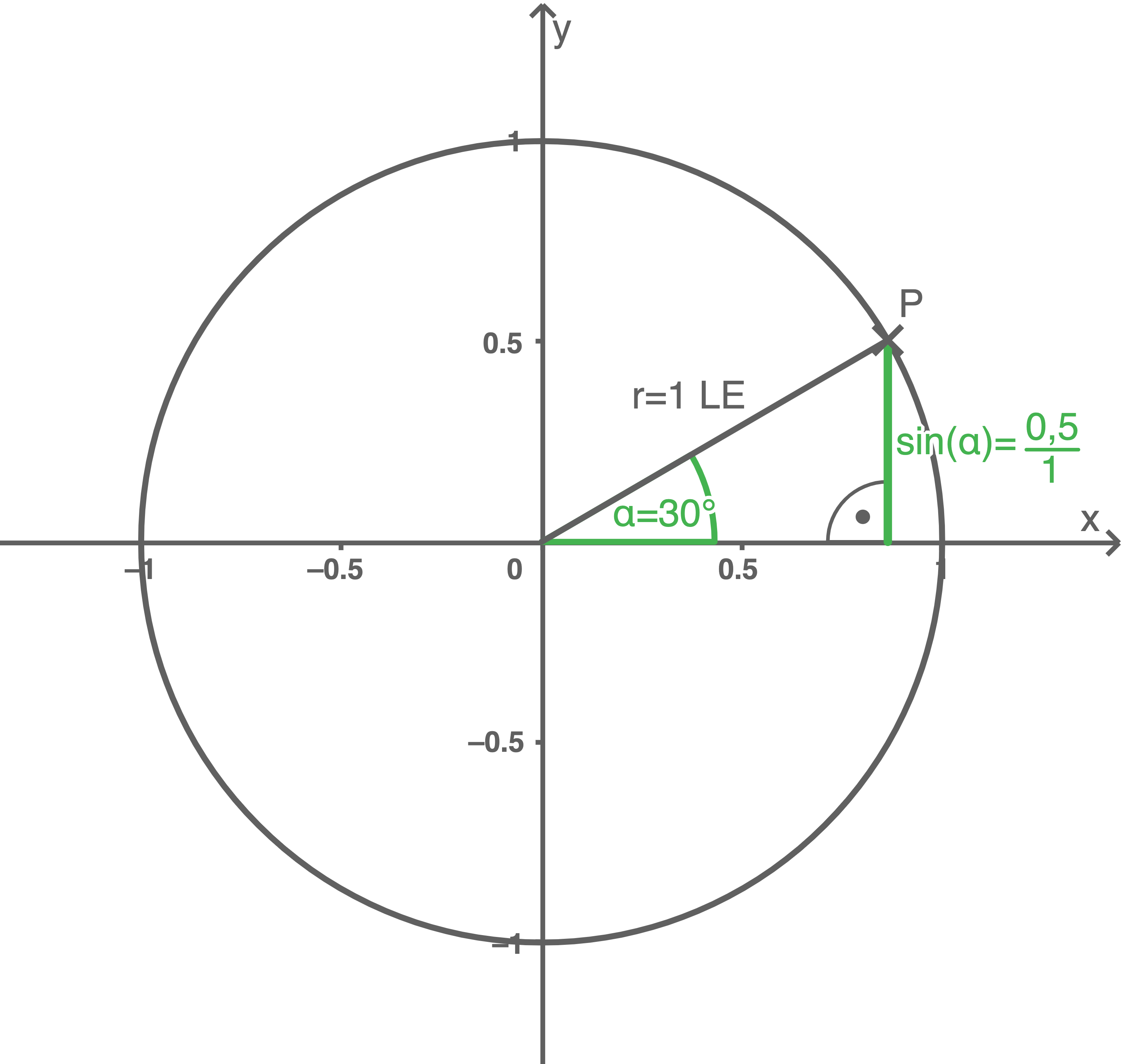 Dem Winkel
Dem Winkel  wird der Wert 0,5 zugeordnet, da die Hypotenuse im rechtwinkligen Dreieck die Länge 1 hat.
wird der Wert 0,5 zugeordnet, da die Hypotenuse im rechtwinkligen Dreieck die Länge 1 hat.
 Die Lage des Punktes
Die Lage des Punktes  wird nun auf dem Kreis verändert. Somit wird jedem Wert von
wird nun auf dem Kreis verändert. Somit wird jedem Wert von  ein Wert
ein Wert  zugeordnet.
Verändert man den Wert von
zugeordnet.
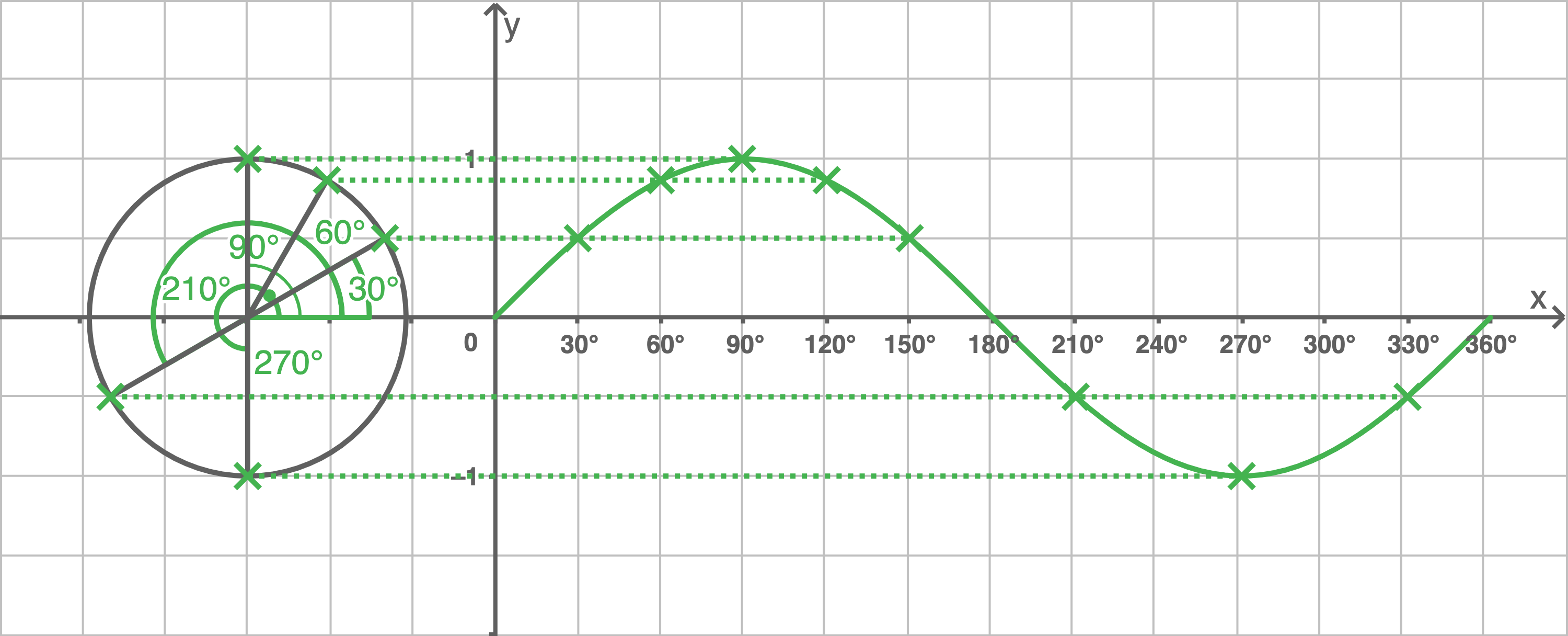
Verändert man den Wert von  in 30°-Schritten, so erhält man folgende Werte für
in 30°-Schritten, so erhält man folgende Werte für 
Die Sinusfunktion ist eine trigonometrische Funktion und ihr Graph heißt Sinuskurve.

- Wenn
dann ist die Gegenkathete 0,5 LE lang.
- Wenn
dann ist die Gegenkathete 1 LE lang.
Begründung
Mit dem sogenannten Einheitskreis kann gezeigt werden, wie sich jedem Wert von
| 0° | 0 |
| 30° | 0,5 |
| 60° | 0,87 |
| 90° | 1 |
| 120° | 0,87 |
| 150° | 0,5 |
| 180° | 0 |
| ... | ... |
| 270° | 1 |
| ... | ... |
| 360° | 0 |

1
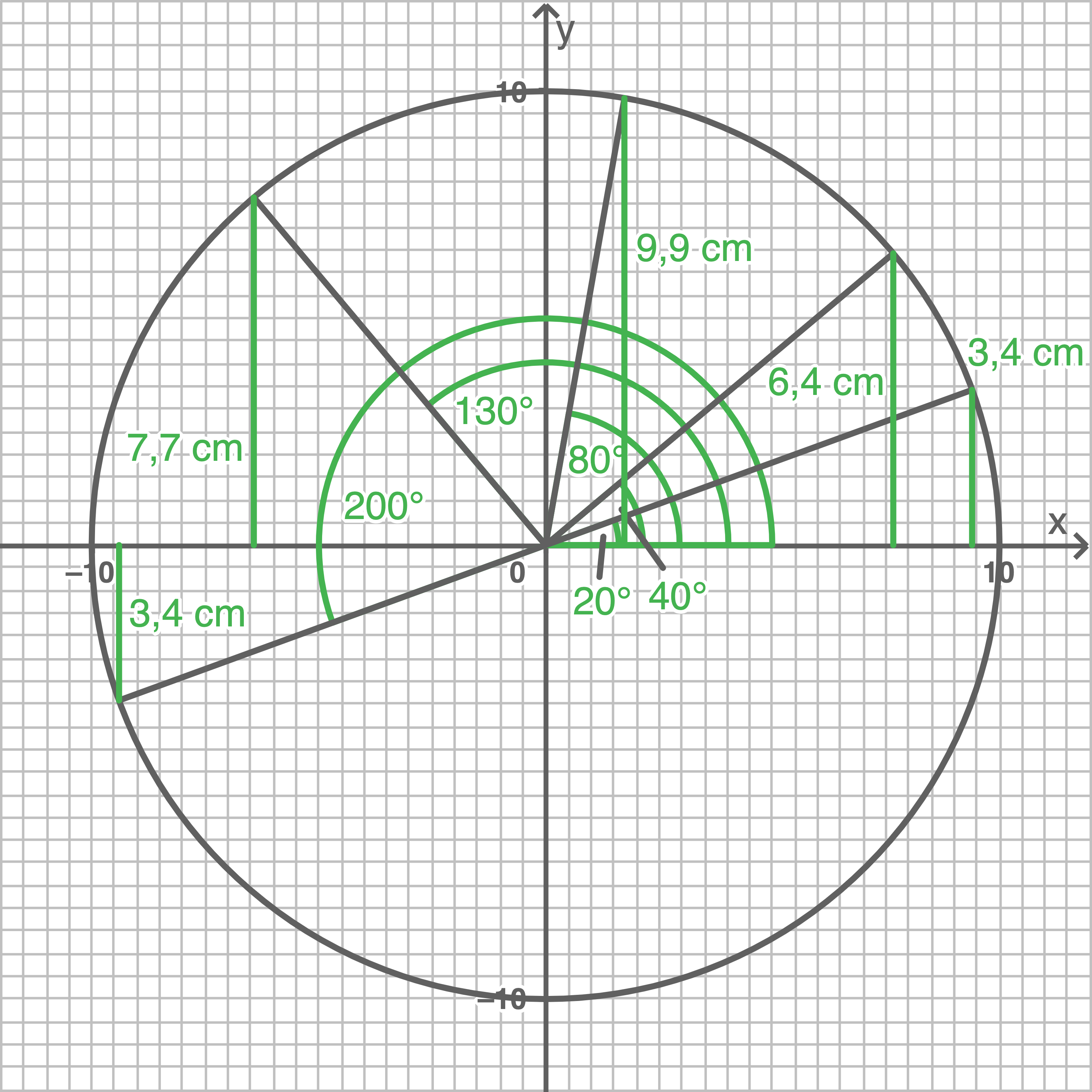
Zeichne einen Kreis mit dem Radius  mit den Winkeln
mit den Winkeln 



 und miss die Sinuswerte. Teile anschließend die Sinuswerte durch
und miss die Sinuswerte. Teile anschließend die Sinuswerte durch  damit du die Sinuswerte des entsprechenden Einheitskreises erhältst.
damit du die Sinuswerte des entsprechenden Einheitskreises erhältst.
Überprüfe deine gemessenen Werte mit dem Taschenrechner.
Überprüfe deine gemessenen Werte mit dem Taschenrechner.
2
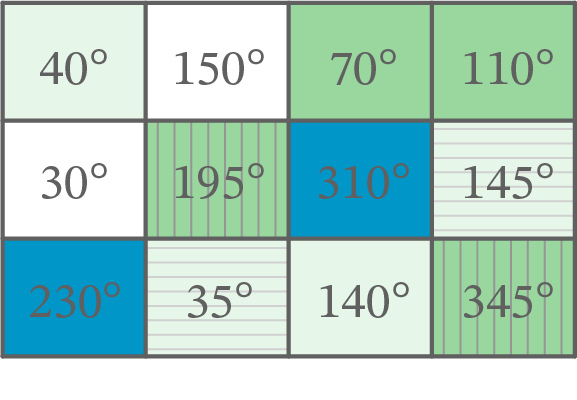
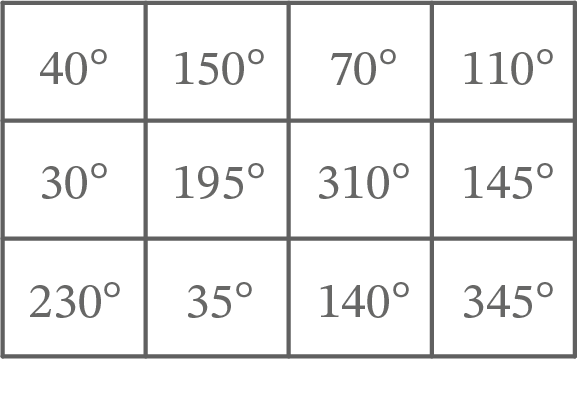
Die Übersicht zeigt verschiedene Winkelgrößen. Welche Winkel haben die gleichen Sinuswerte?

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
2