Exponentialgleichung und Logarithmus
Wie lineare Gleichungen der Form 
gelöst werden, ist bereits bekannt.
Es gibt aber auch Gleichungen der Form 
Hier steht die Variable 
im Exponenten. Solche Gleichungen werden Exponentialgleichungen genannt.
Drei besondere Exponentialgleichungen wurden bereits behandelt:
im Exponenten.
Um Exponentialgleichungen zu lösen, wird der Logarithmus angewendet:
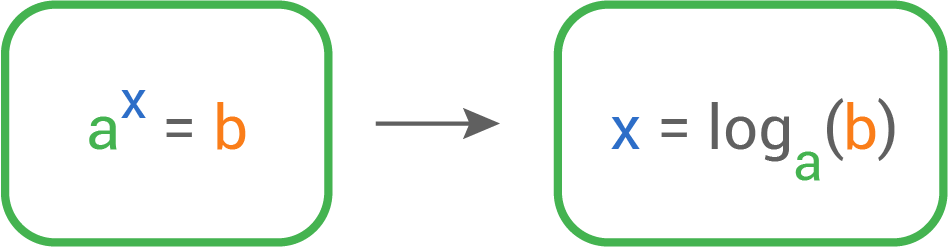Man sagt: x ist der Logarithmus von b zur Basis a, wenn 
und 
Beispiel zum Lösen im Kopf
![\(\begin{array}[t]{rll}
2^x&=&8 \\[5pt]
x&=& \log_2(8) \\[5pt]
x&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/59d87b7fcf6a8ed7d19ec5a555844aea4105f7af20fa1625dac1031a47117cb1_light.svg)
![\(\begin{array}[t]{rll}
4^x&=&16 \\[5pt]
x&=& \log_4(16) \\[5pt]
x&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/42d4995d5d9a53fce0da928bdf123cacb480e243a76da12c4f4bb0efef59bfef_light.svg)
![\(\begin{array}[t]{rll}
3^x&=&729 \\[5pt]
x&=& \log_3(729) \\[5pt]
x&=& 6
\end{array}\)](https://www.schullv.de/resources/formulas/5729f3e4460cec35a192ec1a24be09a86deb43ebbdeec272cd9c59e0e2866666_light.svg)
Weiteres Beispiel zum Lösen mit dem Taschenrechner
![\(\begin{array}[t]{rll}
7^x&=&16807 \\[5pt]
x&=& \log_7(16807) \\[5pt]
x&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/eb090b75135f9a8b9d86bb276659e7b4406952fb3553b5741b3c189c2fee9439_light.svg)
gelöst werden, ist bereits bekannt.
Es gibt aber auch Gleichungen der Form Hier steht die Variable im Exponenten. Solche Gleichungen werden Exponentialgleichungen genannt.
Drei besondere Exponentialgleichungen wurden bereits behandelt:
- Zinseszinsen:
- Exponentielles Wachstum:
- Exponentielle Abnahme:
im Exponenten.
Um Exponentialgleichungen zu lösen, wird der Logarithmus angewendet:
und
Beispiel zum Lösen im Kopf
Frage zum Lösen: Mit welcher Zahl muss 
potenziert werden, um 
zu erhalten?
Die Antwort ist 3, denn: 
Weiteres Beispiel zum Lösen im Kopf
potenziert werden, um zu erhalten?
Die Antwort ist 3, denn:
Frage zum Lösen: Mit welcher Zahl muss 
potenziert werden, um 
zu erhalten?
Die Antwort ist 2, denn: 
Beispiel zum Lösen mit dem Taschenrechner
potenziert werden, um zu erhalten?
Die Antwort ist 2, denn:
Weiteres Beispiel zum Lösen mit dem Taschenrechner
1
Löse die Gleichungen im Kopf.
a)
b)
c)
d)
2
Löse die Gleichungen mit dem Taschenrechner.
a)
b)
c)
d)
3
Ella legt 
bei ihrer Bank an. Die Bank bietet ihr einen Zinssatz von 
an.
bei ihrer Bank an. Die Bank bietet ihr einen Zinssatz von an.
a)
Wie viele Jahre muss Ella ihr Geld bei der Bank anlegen, damit sie ein Kapital von 
hat?
hat?
b)
Eine andere Bank würde Ella einen Zinssatz von 
anbieten. Wie viele Jahre würde sich Ella bei dieser Bank sparen, um auf zu kommen?
anbieten. Wie viele Jahre würde sich Ella bei dieser Bank sparen, um auf zu kommen?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
![\(\begin{array}[t]{rll}
x&=& \log_{10}(100) \\[5pt]
x&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/6d50d1e1d34b832e4db5848fedc5e9e08c7ef610724656d9746c075b604596ba_light.svg)
b)
![\(\begin{array}[t]{rll}
x&=& \log_{6}(36) \\[5pt]
x&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/c03e3a615e5e4a5fd788ad8dd4a20ac9a938e25b52b5323e726653abc25538be_light.svg)
c)
![\(\begin{array}[t]{rll}
x&=& \log_{4}(64) \\[5pt]
x&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/873c82300d3c4b180ca0539cc15a2ffbaf73ce40991a404fc2b9e75725edb40f_light.svg)
d)
![\(\begin{array}[t]{rll}
x&=& \log_{2}(128) \\[5pt]
x&=& 7
\end{array}\)](https://www.schullv.de/resources/formulas/9d9b36d441970b27b868df077d8b57d9584c378b65d781862bec1d54e9d28b0a_light.svg)
2
a)
![\(\begin{array}[t]{rll}
x&=& \log_{6}(10\,077\,696) \\[5pt]
x&=& 9
\end{array}\)](https://www.schullv.de/resources/formulas/2cbeaaa91b2ffc54d9d341f98a22c65a71eb7a1849c75b794b79b0d312030c62_light.svg)
b)
![\(\begin{array}[t]{rll}
x&=& \log_{4}(4\,096) \\[5pt]
x&=& 6
\end{array}\)](https://www.schullv.de/resources/formulas/a9bd25dd8fcca86f2d6aca6c6f4522afdeee0cf2e5f2aaac0a9e84a08a103c08_light.svg)
c)
![\(\begin{array}[t]{rll}
x&=& \log_{11}(161\,051) \\[5pt]
x&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/b00b94438cba5914cc97794500a776075293b79dd870dd4102d7d389c4ef829c_light.svg)
d)
![\(\begin{array}[t]{rll}
x&=& \log_{3}(43\,046\,721) \\[5pt]
x&=& 16
\end{array}\)](https://www.schullv.de/resources/formulas/02f9506c4744706841c10586e8b0a07e832676443ef02cbd52985bf810555f8a_light.svg)
3
a)
![\(\begin{array}[t]{rll}
K_n&=&K_0\cdot q^n \\[5pt]
K_n&=& K_0\cdot \left(1+\dfrac{p}{100}\right)^n &\quad \scriptsize \mid\;:K_0 \\[5pt]
\dfrac{K_n}{K_0}&=& \left(1+\dfrac{p}{100}\right)^n \\[5pt]
\left(1+\dfrac{p}{100}\right)^n&=& \dfrac{K_n}{K_0} \\[5pt]
\left(1+\dfrac{2,5}{100}\right)^n&=& \dfrac{1\,250\,€}{900\,€} \\[5pt]
1,025^n&=& \dfrac{1\,250\,€}{900\,€} \\[5pt]
n&=& \log_{1,025}\left(\dfrac{1\,250\,€}{900\,€}\right) \\[5pt]
n&=& 13 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ca3b985f14969925995f7c2f00d81e53c7251b1b39086fe8d9cc96522fef7334_light.svg)
Ella müsste ihr Geld 13 Jahre bei der Bank anlegen, um auf Kapital zu kommen.
b)
![\(\begin{array}[t]{rll}
K_n&=&K_0\cdot q^n \\[5pt]
K_n&=& K_0\cdot \left(1+\dfrac{p}{100}\right)^n &\quad \scriptsize \mid\;:K_0 \\[5pt]
\dfrac{K_n}{K_0}&=& \left(1+\dfrac{p}{100}\right)^n \\[5pt]
\left(1+\dfrac{p}{100}\right)^n&=& \dfrac{K_n}{K_0} \\[5pt]
\left(1+\dfrac{2,99}{100}\right)^n&=& \dfrac{1\,250\,€}{900\,€} \\[5pt]
1,0299^n&=& \dfrac{1\,250\,€}{900\,€} \\[5pt]
n&=& \log_{1,0299}\left(\dfrac{1\,250\,€}{900\,€}\right) \\[5pt]
n&=& 11 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ce9e8b8ed301135895767655a8e48687004593d7bba66ccbb03c62e689dcb1d1_light.svg)
Würde Ella ihr Geld bei dieser Bank anlegen, würde sie sich 2 Jahre sparen, um auf Kapital zu kommen.