Teil B2

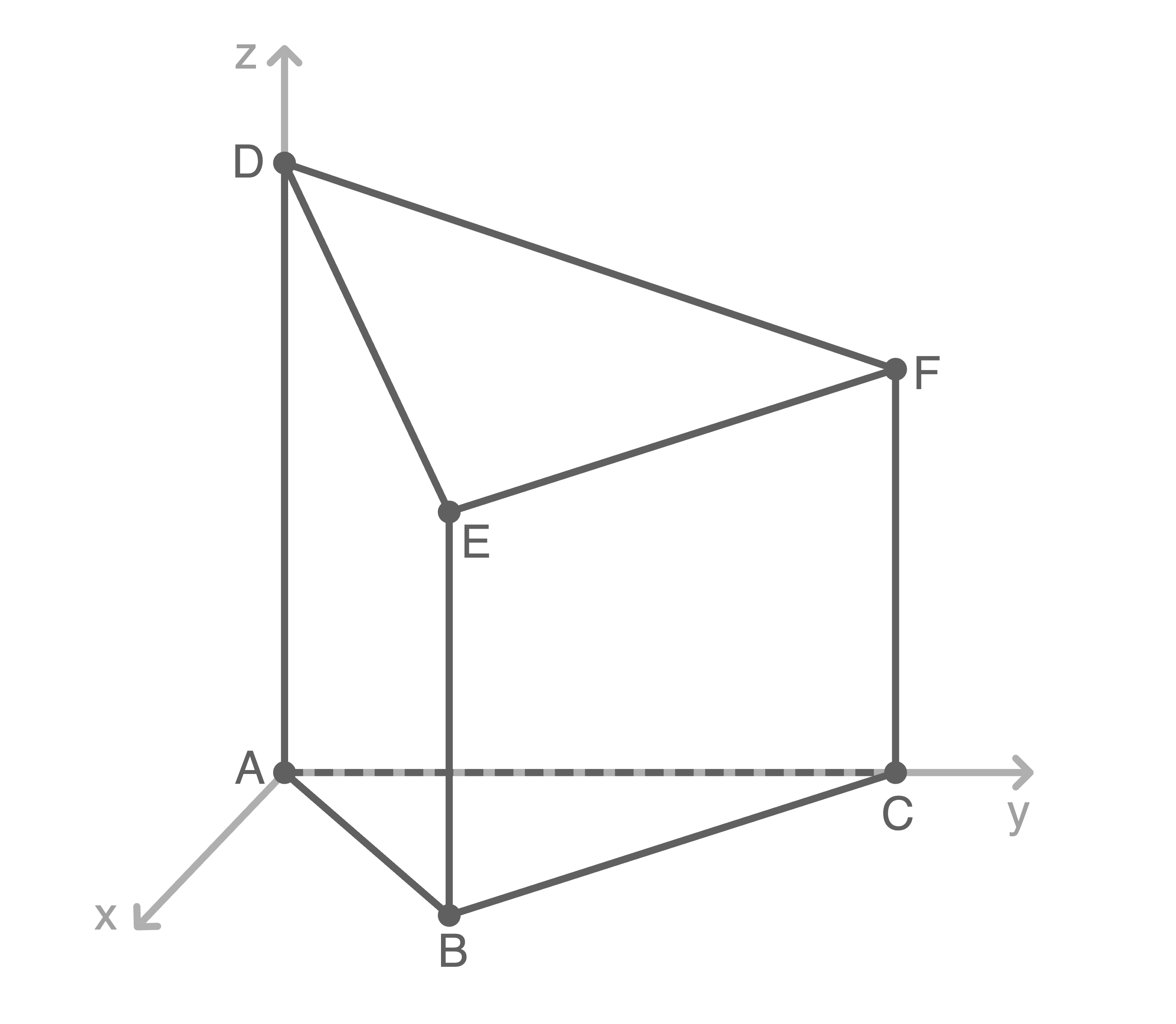
Die Abbildung zeigt den Körper $ABCDEF$ mit den Punkten $A(0\mid 0\mid 0),$ $B(2\mid 1,5 \mid 0),$ $C(0\mid 3\mid 0),$ $D(0\mid 0\mid 3),$ $E(2\mid 1,5 \mid 2)$ und $F(0\mid 3\mid 2)$ in einem kartesischen Koordinatensystem.

Die Grundfläche des Körpers liegt in der $xy$ -Ebene.

2.1

Gib eine Gleichung der Gerade an, auf der die Punkte $D$ und $E$ liegen.

Weise nach, dass das Viereck $BCFE$ ein Rechteck ist.

(5 BE)

2.2

Zeige, dass das Dreieck $DEF$ in der Ebene mit der Gleichung $3 \cdot x+4 \cdot y+12 \cdot z=36$ liegt.

Bestimme die Größe des stumpfen Winkels, den die Flächen $BCFE$ und $DEF$ einschließen.

(6 BE)

2.3

Betrachtet wird der Term $A_G \cdot 2+\dfrac{1}{3} \cdot A_G \cdot(3-2),$ wobei $A_G$ der Flächeninhalt der Grundfläche des Körpers $ABCDEF$ ist.

Gib die Bedeutung des Terms im Zusammenhang mit dem Körper an und begründe die Angabe.

(4 BE)

2.4

Die Gerade durch die Punkte $P(1 \mid 1 \mid 4)$ und $E$ schneidet die $xy$ -Ebene im Punkt $\(E$

Die Gerade durch die Punkte $P$ und $F$ schneidet die $xy$ -Ebene im Punkt $\(F$

Bestimme das Verhältnis der Längen der Strecken $\(\overline{E$ und $\overline{E F}.$

(5 BE)

Eine Firma stellt aus Modulen in Form des dargestellten Körpers Pavillons her.

Kunden, die einen Pavillon kaufen, können sich zwischen Selbstaufbau und Komplettmontage entscheiden. Außerdem kann der Pavillon mit oder ohne Farbanstrich geliefert werden.

Erfahrungsgemäß entscheiden sich $80 \,\%$ aller Kunden für einen Pavillon mit Farbanstrich. Nur $5 \,\%$ aller Kunden kaufen einen Pavillon ohne Farbanstrich und wählen den Selbstaufbau. $30 \,\%$ aller Kunden entscheiden sich für Selbstaufbau.

2.5

Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.

Gib die Wahrscheinlichkeit der folgenden Ereignisse an:

Ereignis A: Ein zufällig ausgewählter Kunde wählt die Komplettmontage.

Ereignis B: Ein zufällig ausgewählter Kunde kauft einen Pavillon mit Farbanstrich und wählt den Selbstaufbau.

(5 BE)

2.6

Berechne die zu erwartende Anzahl der Kunden unter 20 zufällig ausgewählten Kunden, die einen Selbstaufbau wählen.

(2 BE)

2.7

Es werden die Kunden betrachtet, die den Pavillon ohne Farbanstrich kaufen.

Bestimme unter diesen den Anteil der Kunden, die sich für eine Komplettmontage entscheiden.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Gleichung angeben

$\begin{array}[t]{rll} g: \overrightarrow{x}&=& \overrightarrow{OD}+t\cdot \overrightarrow{DE} &\\[5pt] &=& \pmatrix{0\\0\\3} +t\cdot \pmatrix{2\\1,5\\-1} \end{array}$

Rechteck nachweisen

Um nachzuweisen, dass das Viereck $B C F E$ ein Rechteck ist, muss gezeigt werden, dass die gegenüberliegenden Seiten jeweils gleich lang sind und dass die Winkel zwischen benachbarten Seiten rechte Winkel sind.

Seitenlängen berechnen:

$|\overline{BC}|=2,5$

Rechenweg anzeigen

$|\overline{BE}|=2$

Rechenweg anzeigen

$|\overline{EF}|=2,5$

Rechenweg anzeigen

$|\overline{CF}|=2$

Rechenweg anzeigen

Somit gilt für die gegenüberliegenden Seiten des Vierecks $|\overline{BC}|=|\overline{EF}|$ und $|\overline{BE}|= |\overline{CF}|.$

Rechten Winkel überprüfen:

$\begin{array}[t]{rll} \overrightarrow{BC} \circ \overrightarrow{BE} &=& \pmatrix{-2\\1,5\\0} \circ \pmatrix{0\\0\\2}& \\[5pt] &=& (-2)\cdot 0+1,5\cdot 0+0\cdot 2& \\[5pt] &=& 0 \end{array}$

Somit schließen die Seiten $\overline{BC}$ und $\overline{BE}$ einen rechten Winkel ein. Da die gegenüberliegenden Seiten des Vierecks jeweils gleich lang sind, müssen folglich auch alle anderen Winkel innerhalb des Vierecks rechte Winkel sein.

Das Viereck $BCFE$ ist somit ein Rechteck.

2.2

Lage nachweisen

Punktprobe mit $D,E$ und $F:$

$\begin{array}[t]{rll} 3\cdot 0+4\cdot 0+12\cdot 3&=& 36& \\[5pt] 36&=& 36 \end{array}$

$\begin{array}[t]{rll} 3\cdot 2+4\cdot 1,5+12\cdot 2&=& 36& \\[5pt] 36&=& 36 \end{array}$

$\begin{array}[t]{rll} 3\cdot 0+4\cdot 3+12\cdot 2&=& 36& \\[5pt] 36&=& 36 \end{array}$

Da die drei Eckpunkte $D,E$ und $F$ in der Ebene mit der gegebenen Gleichung liegen, liegt folglich auch das gesamte Dreieck $DEF$ in der Ebene.

Größe des Winkels bestimmen

Ein Normalenvektor der Ebene $BCFE$ ergibt sich aus dem Kreuzprodukt von zwei Vektoren der Ebene:

$\begin{array}[t]{rll} \overrightarrow{n_{BCFE}}&=& \overrightarrow{BC} \times \overrightarrow{BE} & \\[5pt] &=& \pmatrix{-2\\1,5\\0} \times \pmatrix{0\\0\\2} & \\[5pt] &=& \pmatrix{1,5\cdot 2-0\cdot 0\\0\cdot 0-(-2)\cdot 2\\(-2)\cdot 0-1,5\cdot 0} & \\[5pt] &=& \pmatrix{3\\4\\0} \end{array}$

Das Kreuzprodukt kann alternativ auch mit dem CAS berechnet werden.

Ein Normalenvektor der Ebene $DEF$ kann direkt aus der Koordinatengleichung abgelesen werden und ergibt sich zu $\overrightarrow{n_{DEF}}=\pmatrix{3\\4\\12}.$

Für den Winkel $\alpha,$ den die beiden Flächen einschließen, gilt nun:

$\alpha \approx 67,38^\circ$

Rechenweg anzeigen

Die Größe des stumpfen Winkels $\beta$ ergibt sich somit zu:

$\begin{array}[t]{rll} \beta&=& 180^\circ - \alpha& \\[5pt] &=& 180^\circ - 67,38^\circ& \\[5pt] &=& 112,62^\circ \end{array}$

2.3

Der Körper lässt sich in ein Prisma und eine Pyramide mit dreieckiger Grundfläche unterteilen.

$A_G$ entspricht dem Flächeninhalt der Grundfläche $ABC$ des Körpers, welche in der $xy$ -Ebene liegt. Der Inhalt dieser entspricht aufgrund der Parallelität ebenso dem Flächeninhalt der Grundfläche der Pyramide.

$A_G \cdot 2$ beschreibt das Volumen des Prismas mit der Grundfläche $A_G$ und der Höhe 2. Die Höhe ergibt sich aus der Differenz der $z$ -Koordinaten der Punkte $B$ und $E:$ $z_E-z_B=2-0=2.$

Der Term $\dfrac{1}{3} \cdot A_G \cdot(3-2)$ beschreibt den Flächeninhalt der dreiseitigen Pyramide, wobei der Ausdruck $(3-2)$ die Höhe $h$ der Pyramide beschreibt. Für diese gilt nämlich: $h=z_D-z_E=3-2.$

Insgesamt beschreibt der Term also das Volumen des gesamten Körpers $ABCDEF.$

2.4

1. Schritt: Geradengleichungen aufstellen

Die Gerade $g$ durch die Punkte $P$ und $E$ wird durch die folgende Gleichung beschrieben:

$\begin{array}[t]{rll} g: \quad \overrightarrow{x}&=& \overrightarrow{OP}+t\cdot \overrightarrow{PE} & \\[5pt] &=& \pmatrix{1\\1\\4}+t\cdot \pmatrix{1\\0,5\\-2} \end{array}$

Die Gerade $h$ durch die Punkte $P$ und $F$ wird durch die folgende Gleichung beschrieben:

$\begin{array}[t]{rll} h: \quad \overrightarrow{x}&=& \overrightarrow{OP}+s\cdot \overrightarrow{PF} & \\[5pt] &=& \pmatrix{1\\1\\4}+s\cdot \pmatrix{-1\\2\\-2} \end{array}$

2. Schritt: Schnittpunkt $\(\boldsymbol{E$ bestimmen

Für den Schnittpunkt der Geraden $g$ mit der $xy$ -Ebene gilt:

$g: \quad \pmatrix{x\\y\\0}=\pmatrix{1\\1\\4}+t\cdot \pmatrix{1\\0,5\\-2}$

Aus der dritten Zeile ergibt sich:

$\begin{array}[t]{rll} 0&=& 4-2t&\quad \scriptsize \mid\; +2t\\[5pt] 2t&=& 4&\quad \scriptsize \mid\; :2 \\[5pt] t&=& 2 \end{array}$

Einsetzen in die Geradengleichung liefert:

$\(\begin{array}[t]{rll} g: \quad \overrightarrow{OE$

Die Koordinaten von $\(E$ folgen also mit $\(E$

3. Schritt: Schnittpunkt $\(\boldsymbol{F$ bestimmen

Für den Schnittpunkt der Geraden $h$ mit der $xy$ -Ebene gilt:

$h: \quad \pmatrix{x\\y\\0}=\pmatrix{1\\1\\4}+s\cdot \pmatrix{-1\\2\\-2}$

Aus der dritten Zeile ergibt sich analog zum 2. Schritt $s=2.$

Einsetzen in die Geradengleichung liefert:

$\(\begin{array}[t]{rll} h: \quad \overrightarrow{OF$

Die Koordinaten von $\(F$ folgen also mit $\(F$

4. Schritt: Längen der Strecken berechnen

$\begin{array}[t]{rll} |\overline{EF}|&=& \left|\pmatrix{0-2\\3-1,5\\2-2} \right| & \\[5pt] &=& \sqrt{(-2)^2+1,5^2+0^2}& \\[5pt] &=& 2,5 \;[ \text{LE}] & \\[5pt] \end{array}$

$\(\begin{array}[t]{rll} |\overline{E$

5. Schritt: Verhältnis bestimmen

$\(\dfrac{|\overline{E$

Die Längen der Strecken $\(\overline{E$ und $\overline{EF}$ stehen im Verhältnis $2:1$ zueinander.

2.5

Vierfeldertafel erstellen

$S:$ Kunde wählt Selbstaufbau

$F:$ Kunde wählt Farbanstrich

Einsetzen der bekannten Informationen in eine Vierfeldertafel ergibt:

	$\color{#fff}{F}$	$\color{#fff}{\overline{F}}$	Gesamt
$\color{#fff}{S}$		$5\,\%$	$30\,\%$
$\color{#fff}{\overline{S}}$
Gesamt	$80\,\%$

Ausfüllen der restlichen Felder:

	$\color{#fff}{F}$	$\color{#fff}{\overline{F}}$	Gesamt
$\color{#fff}{S}$	$25\,\%$	$5\,\%$	$30\,\%$
$\color{#fff}{\overline{S}}$	$55\,\%$	$15\,\%$	$70\,\%$
Gesamt	$80\,\%$	$20\,\%$	$100\,\%$

Wahrscheinlichkeit angeben

$P(A)=P(\overline{S})=70\,\%$

$P(B)=P(S \cap F)=25\,\%$

2.6

Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Kunde einen Selbstaufbau wählt, beträgt $30\,\%.$

Somit ergibt sich die zu erwartende Anzahl der Kunden unter 20 zufällig ausgewählten Kunden, die einen Selbstaufbau wählen, mit:

$20\cdot 0,3= 6$

2.7

$\begin{array}[t]{rll} P(\overline{S}\mid \overline{F})&=& \dfrac{P(\overline{S}\cap \overline{F})}{P(\overline{F})} & \\[5pt] &=& \dfrac{15\,\% }{20\,\% }& \\[5pt] &=& 0,75 \end{array}$

Unter dem Anteil der Kunden, die einen Pavillon ohne Farbanstrich kaufen, entscheiden sich $75\,\%$ für eine Komplettmontage.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?