Teil A

In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1

Eine in $\mathbb{R}$ definierte Funktion $f$ besitzt an der Stelle $x=2$ den Anstieg 12. Eine mögliche Funktionsgleichung von $f$ lautet:

	$f(x)=1$
	$f(x)=x$
	$f(x)=x^2$
	$f(x)=x^3$
	$f(x)=x^4$

1.2

Gegeben ist die Funktion $f$ mit $f(x) = \dfrac{27-x^2}{3-x}$ $(x\in D_f).$
Es gilt:

	Die Nullstelle von $f$ ist $x=3.$
	Der größtmögliche Definitionsbereich von $f$ ist $\mathbb{R}.$
	Der Graph von $f$ besitzt die waagerechte Asymptote mit der Gleichung $y=3.$
	Der Graph von $f$ besitzt die senkrechte Asymptote mit der Gleichung $x=3.$
	Der Schnittpunkt des Graphen von $f$ mit der $y$ -Achse hat die Koordinaten $(0\mid 3).$

1.3

Gegeben sind der Vektor $\overrightarrow{AB} = \pmatrix{4\\8\\-2}$ und der Punkt $B(6\mid -4\mid 2).$
Der Punkt $A$ besitzt die Koordinaten:

	$(-2\mid 4\mid 4)$
	$(-2\mid -12\mid 2)$
	$(-6\mid -4\mid 4)$
	$(2\mid 12\mid 0)$
	$(2\mid -12\mid 4)$

1.4

Gegeben sind die Vektoren

$\overrightarrow{a}= \pmatrix{1\\ 2\\3}$ und $\overrightarrow{b} = \pmatrix{0\\1\\t}.$

Für welchen reellen Wert von $t$ sind die Vektoren $\overrightarrow{a}$ und $\overrightarrow{b}$ orthogonal zueinander?

	$t= -\frac{3}{2}$
	$t= -\frac{2}{3}$
	$t=0$
	$t= \frac{2}{3}$
	$t= \frac{3}{2}$

1.5

Gegeben ist die vollständige Wahrscheinlichkeitsverteilung einer Zufallsgröße $X$ mit der positiven reellen Zahl $a.$

$X=x_i$	$P(X=x_i)$
$1$	$a$
$2$	$0,1$
$3$	$0,3$
$4$	$2\cdot a$

Es gilt:

	$a+2\cdot a = 1$
	$3\cdot a = 0,4$
	$a=0,2$
	$P(X\leq 2) = 0,1$
	$P(X\lt 1) = 0,3$

Für Aufgabe 1 erreichbare BE-Anzahl: 5

Gegeben sind zwei einander schneidende Geraden

$g: \overrightarrow{x} = \pmatrix{3\\2\\4} +r\cdot \pmatrix{1\\-1\\0}$ und $h: \overrightarrow{x} = \pmatrix{3\\3\\3} + s\cdot \pmatrix{1\\0\\-1}$ mit $r,s \in \mathbb{R}.$

2.1

Berechne die Koordinaten des Schnittpunkts von $g$ und $h.$

(3 BE)

2.2

Die Gerade $g$ und $h$ liegen in einer Ebene.
Berechne die Koordinaten eines Normalenvektors dieser Ebene.

(2 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)= x^3-x.$

3.1

Einer der folgenden Graphen I,II und III stellt $f$ dar.
Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.

Graph einer mathematischen Funktion mit den Achsen x und y.

Graf einer mathematischen Funktion mit x- und y-Achse, zeigt eine grüne Kurve.

Graph einer Funktion mit x- und y-Achse, zeigt eine steigende Kurve.

(2 BE)

3.2

Berechne den Inhalt der Fläche, die der Graph von $f$ und die $x$ -Achse einschließen.

(3 BE)

Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit

$f(x)=3\cdot x\cdot \mathrm e^x.$

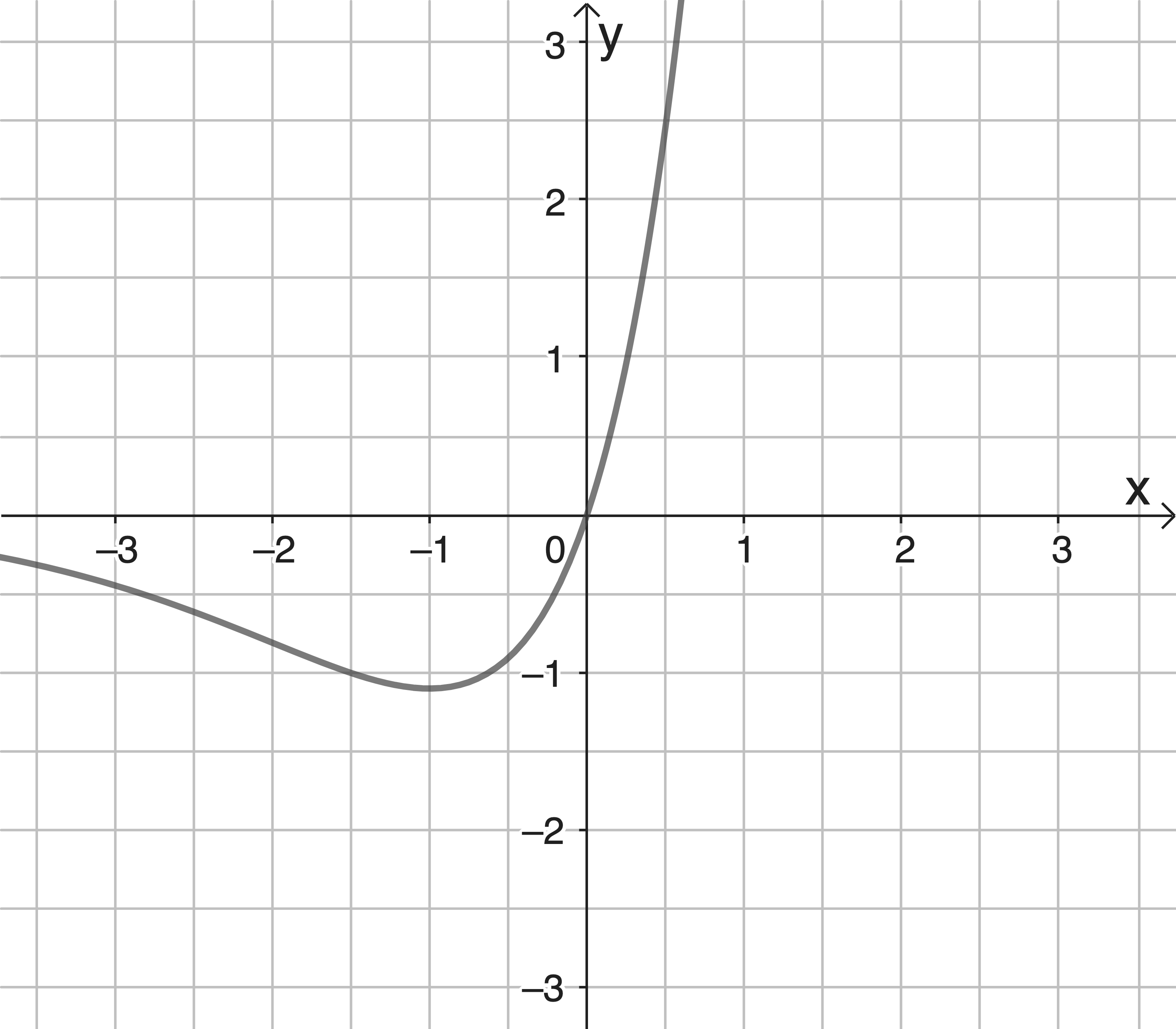
Graf einer mathematischen Funktion im Koordinatensystem mit Achsen und Gitterlinien.

4.1

Die Funktion $f$ hat genau eine Extremstelle. Zeige rechnerisch, dass diese $-1$ ist.

(2 BE)

4.2

Der Graph einer Stammfunktion $F$ von $f$ verläuft durch den Koordinatenursprung.
Skizziere - ausschließlich unter Verwendung des Graphen von $f$ - den Graphen von $F$ in der Abbildung.

(3 BE)

Im Folgenden werden zwei Würfel stets gemeinsam geworfen.
Bei jedem der beiden Würfel sind die Seiten mit den Zahlen von 1 bis 6 durchnummeriert.

5.1

Die beiden Würfel werden einmal geworfen.
Begründe, dass die Wahrscheinlichkeit dafür, dass dabei keine 6 auftritt, $\frac{25}{36}$ beträgt.

(2 BE)

5.2

Die beiden Würfel werden 36-mal geworfen. Die binomialverteilte Zufallsgröße $X$ gibt die Anzahl der Würfe an, bei denen keine 6 auftritt.

Begründe für jede der folgenden Abbildungen, dass sie nicht die Wahrscheinlichkeitsverteilung von $X$ zeigt.

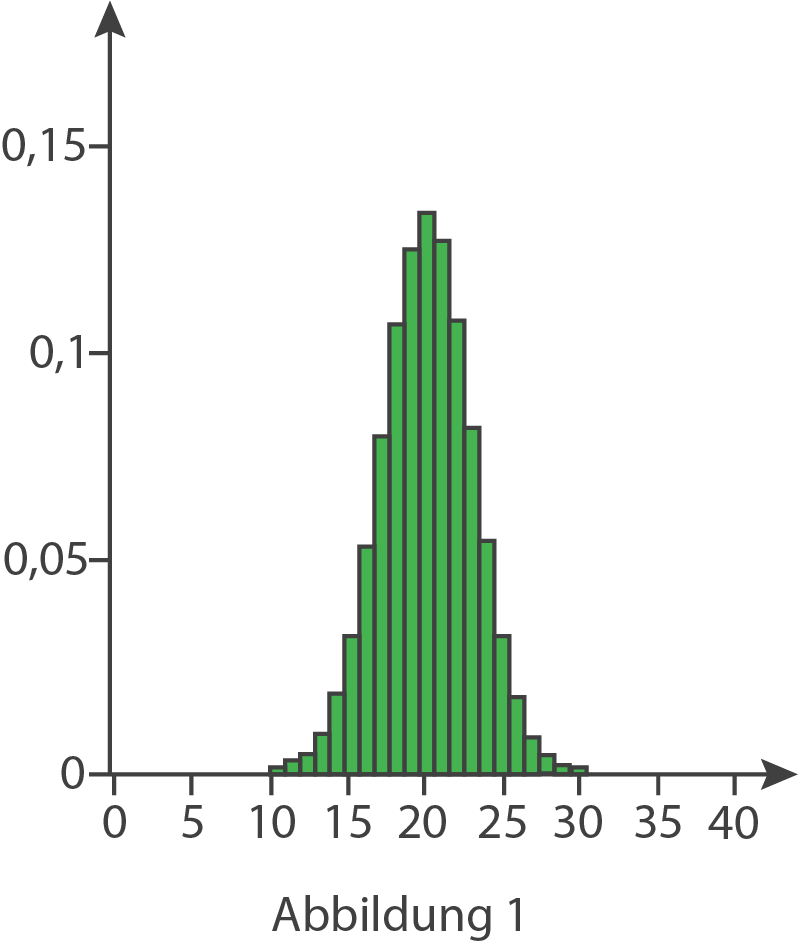
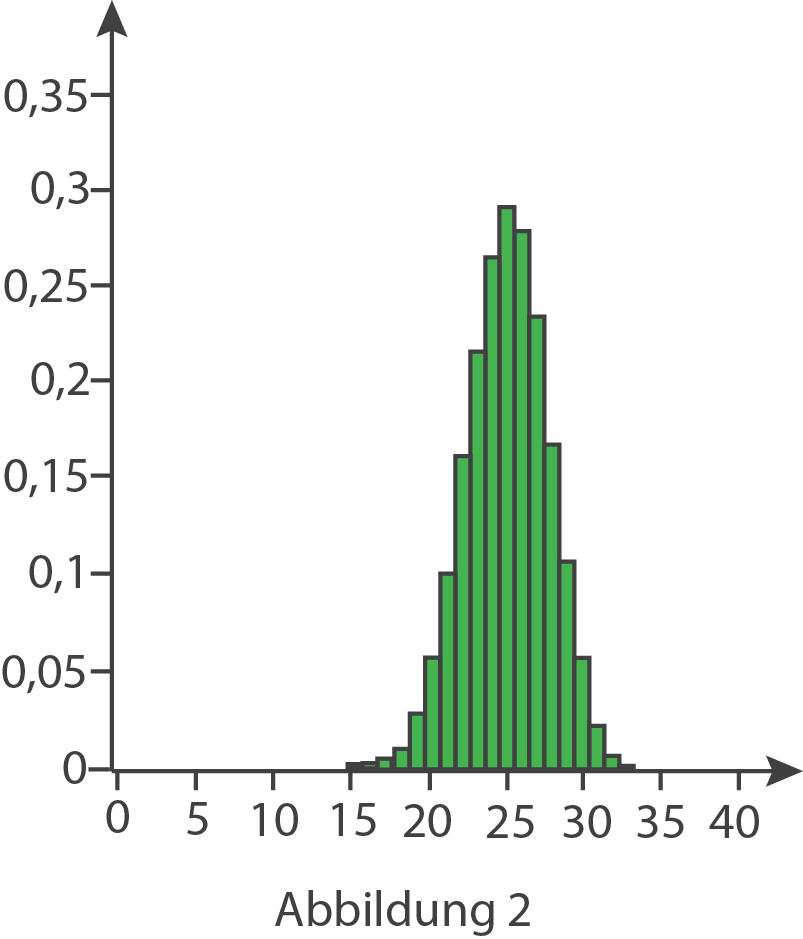
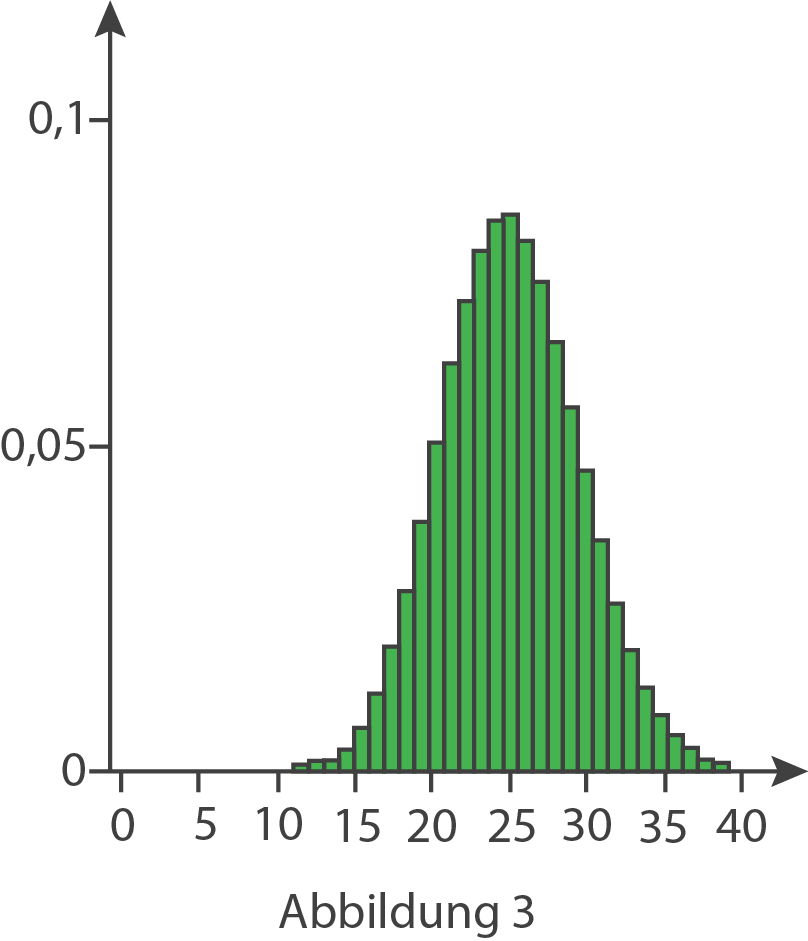
(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

1.1

$\(\begin{array}[t]{rll} f(x)&=& x^3 \\[5pt] f$

Eine mögliche Funktionsgleichung von $f$ lautet somit $f(x)=x^3$ .

1.2

Die Funktion $f$ hat bei $x=3$ eine Definitionslücke und somit an dieser Stelle eine senkrechte Asymptote. Die vierte Antwortmöglichkeit ist also richtig.

1.3

Der Vektor $\overrightarrow{AB}$ lässt sich wie folgt berechnen:

Vollständigen Rechenweg anzeigen

$\overrightarrow{AB}=\pmatrix{6-a_1\\-4-a_2\\2-a_3}=\pmatrix{4\\8\\-2}$

Daraus ergibt sich: $a_1 = 2,$ $a_2 = -12$ und $a_3 = 4.$

Der Punkt $A$ besitzt die Koordinaten $(2\mid -12\mid 4)$ und die letzte Antwortmöglichkeit ist richtig.

1.4

Die Vektoren $\overrightarrow a$ und $\overrightarrow b$ sind zueinander orthogonal, wenn ihr Skalarprodukt null ergibt.

$\pmatrix{1\\2\\3} \circ \pmatrix{0\\1\\t} =0$

$\begin{array}[t]{rll} 1 \cdot 0+2\cdot 1+ 3\cdot t&=& 0&\quad \scriptsize \\[5pt] 2+3t&=& 0&\quad \scriptsize \mid -2\\[5pt] 3t&=& -2&\quad \scriptsize \mid :3 \\[5pt] t&=& -\dfrac{2}{3} \end{array}$

Für $t=-\dfrac{2}{3}$ sind die beiden Vektoren orthogonal zueinander.

1.5

Es gilt: $P(X=1)+P(X=2)+P(X=3)$ $+P(X=4)=1$

Daraus folgt:

Vollständigen Rechenweg anzeigen

$a=0,2$

Lösung 2

2.1

$\pmatrix{3\\2\\4} + r\pmatrix{1\\-1\\0}$ $= \pmatrix{3\\3\\3} + s\pmatrix{1\\0\\-1}$

$\begin{array}[t]{rll} \text{I}:& 3+r&=& 3+s&\quad \scriptsize \\[5pt] \text{II:}& 2-r&=& 3&\quad \scriptsize \mid -2 \mid \cdot (-1)\\[5pt] & r&=& -1&\quad \scriptsize \\[5pt] \text{III:}& 4&=& 3-s&\quad \scriptsize \mid -3\mid \cdot (-1)\\[5pt] & -1&=& s \\[5pt] \end{array}$

$r$ in $g$ einsetzen:

Vollständigen Rechenweg anzeigen

$g: \overrightarrow x =\pmatrix{2\\3\\4}$

Die Geraden $g$ und $h$ schneiden sich im Punkt $S(2\mid 3\mid4)$ .

2.2

Mit dem Kreuzprodukt der beiden Richtungsvektoren von $g$ und $h$ ergibt sich:

Vollständigen Rechenweg anzeigen

$\pmatrix{1\\-1\\0} \times \pmatrix{1\\0\\-1}=\pmatrix{1\\1\\1}$

Lösung 3

3.1

Der Graph II kommt nicht infrage, da $f(0,5)\lt 0$ gilt. Die Funktion beschreibt auch nicht den Graphen III, da $f$ eine ganzrationale Funktion und ihr Graph somit knickfrei sein muss.

3.2

$2\cdot \displaystyle\int_{-1}^{0}(x^3-x)\;\mathrm dx$ $=2\cdot \left[\dfrac{1}{4}x^4-\dfrac{1}{2}x^2\right]_{-1}^0$ $=2 \cdot\left(0-\dfrac{1}{4}+\dfrac{1}{2}\right) =\dfrac{1}{2}$

Der Graph von $f$ schließt mit der $x$ -Achse einen Flächeninhalt von $\dfrac{1}{2}\, \text{FE}$ ein.

Lösung 4

4.1

Überprüfen des notwendigen Kriteriums für Extremstellen:

Mit der Produktregel folgt für die erste Ableitung von $f:$

$\(\begin{array}[t]{rll} f(x)&=& 3\cdot x\cdot \mathrm e^x \\[5pt] f$

Das notwendige Kriterium für Extremstellen von $f$ ist an der Stelle $x=-1$ erfüllt. Dies ist also die einzige Extremstelle von $f.$

4.2

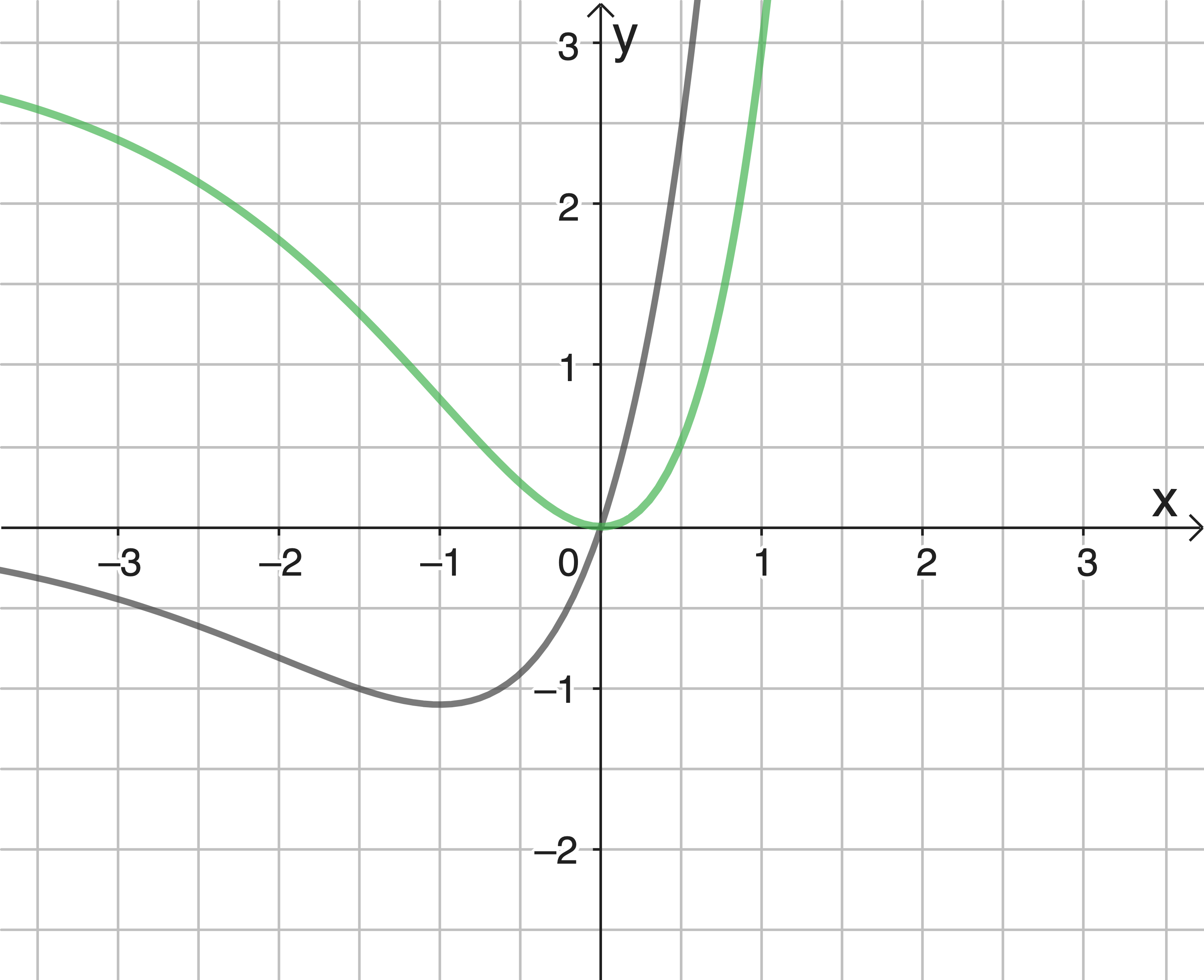
Graph mit zwei Kurven in einem Koordinatensystem, die sich um den Ursprung gruppieren.

Lösung 5

5.1

Die Wahrscheinlichkeit dafür, dass einer der beiden Würfel keine sechs zeigt, beträgt $\dfrac{5}{6}$ .

Für die Wahrscheinlichkeit, dass beide Würfel keine sechs zeigen, folgt dann mit der Pfadmultiplikationsregel:

$\dfrac{5}{6}\cdot\dfrac{5}{6}=\dfrac{25}{36}$ .

5.2

Folgende Kriterien können beachtet werden:

Die höchste Säule muss beim Erwartungswert liegen. Dieser ergibt sich aufgrund der Binomialverteilung zu $36 \cdot \frac{25}{36} = 25.$
Die Summe der dargestellten Werte muss $1$ sein.
Alle Säulen müssen sich im Bereich von $0$ bis $36$ befinden.

Abbildung 1: Die höchste Säule befindet sich bei $20$ und nicht bei $25$ .

Abbildung 2: Die Summe der Wahrscheinlichkeiten ist größer als eins.

Abbildung 3: Die Höhe der Säule bei $37$ ist größer als null.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?