Teil B2

ln einem kartesischen Koordinatensystem sind die Punkte $A(-1|1|2)$ , $B(-1|5|2)$ und $C(-4|3|3)$ gegeben.

2.1

Stelle das Dreieck ${\it ABC}$ im kartesischen Koordinatensystem grafisch dar.

(2 BE)

2.2

Weise nach, dass das Dreieck ${\it ABC}$ in der Ebene mit der Gleichung $\mathrm{x}+3\cdot z=5$ liegt.

(3 BE)

Das Dreieck ${\it ABC}$ stellt modellhaft ein ebenes Sonnensegel dar, das zwischen drei Masten gespannt ist. Der ebene Untergrund liegt in der $x-y-$ Ebene. Eine Längeneinheit im Modell entspricht einem Meter in der Wirklichkeit.

2.3

Damit Regenwasser gut abfließen kann, soll das Sonnensegel so gespannt sein, dass es einen Neigungswinkel von mindestens $17^{\circ}$ zum ebenen Untergrund aufweist.
Untersuche, ob diese Bedingung erfüllt ist.

(3 BE)

2.4

Auf das Sonnensegel treffen zueinander parallele Sonnenstrahlen. Der Schatten des Punktes $A$ auf dem ebenen Untergrund besitzt die Koordinaten $(-5|3|0)$ .
Untersuche, ob die Sonnenstrahlen senkrecht auf das Sonnensegel einfallen.
Bestimme die Koordinaten des Schattens des Punktes $C$ auf dem ebenen Untergrund.

(5 BE)

2.5

Zwischen den Punkten $P(-5|3|5)$ und $\mathrm{O}(0|3|4)$ verläuft geradlinig ein Lichtband.
Zeige, dass jeder Punkt des Lichtbandes durch die Koordinaten $(-5+5\cdot t|3|5-t)$ mit $t\in \mathbb{R},0\leq t\leq 1$ beschrieben werden kann.
Bestimme den Wert von $t$ so, dass der zugehörige Punkt des Lichtbandes den geringsten Abstand zum Punkt $A$ hat.

(7 BE)

Sonnensegel werden entweder aus Naturfasern oder aus Kunstfasern gefertigt. $40\,\%$ der Sonnensegel werden aus Naturfasern hergestellt. Bei Sonnensegeln aus Naturfasern beträgt die Wahrscheinlichkeit für einen Materialfehler $2,3\,\%$ . Die Wahrscheinlichkeit, dass ein Sonnensegel keinen Materialfehler besitzt, beträgt $98\,\%.$

2.6

Bestimme die Wahrscheinlichkeit dafür, dass ein Sonnensegel aus Kunstfasern besteht und einen Materialfehler besitzt.
Ermittle den prozentualen Anteil der Sonnensegel ohne Materialfehler an allen aus Naturfasern hergestellten Sonnensegeln.

(6 BE)

2.7

Nach der Einführung eines neuen Produktionsverfahrens vermutet der Hersteller, dass der Anteil von Sonnensegeln, die einen Materialfehler besitzen, gestiegen ist.
In einem Test soll die Nullhypothese „Der Anteil der Sonnensegel, die einen Materialfehler besitzen, beträgt höchstens $2\,\%$ “ überprüft werden.
Von den $150$ zufällig ausgewählten Sonnensegeln besitzen acht einen Materialfehler.
Untersuche, ob aus diesen Daten auf einem Signifikanzniveau von $5\,\%$ die Vermutung des Herstellers bestätigt werden kann.

(4 BE)

2.1

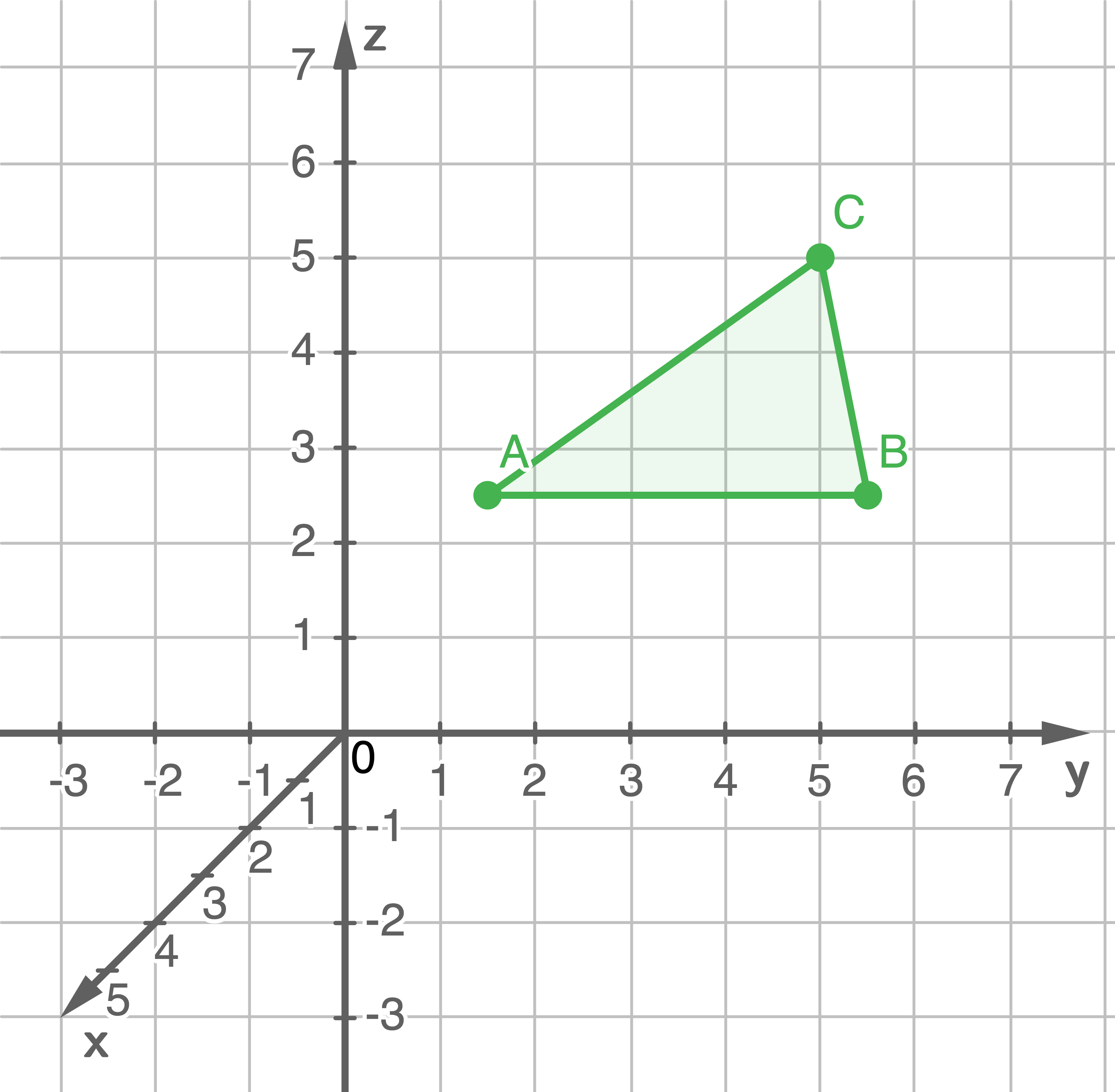
2.2

Durch Einsetzen der Eckpunkte des Dreiecks in die Ebenengleichung folgt:

Punkt A:

$\begin{array}[t]{rll} (-1)+3\cdot 2&=& 5&\quad \scriptsize \; \\[5pt] 5&=&5 \end{array}$

Punkt A liegt folglich in der Ebene.

Punkt B:

$\begin{array}[t]{rll} (-1)+3\cdot 2&=& 5&\quad \scriptsize \; \\[5pt] 5&=&5 \end{array}$

Punkt B liegt folglich in der Ebene.

Punkt C:

$\begin{array}[t]{rll} (-4)+3 \cdot 3&=&5 &\quad \scriptsize \; \\[5pt] 5&=&5 \end{array}$

Punkt C liegt in der Ebene und damit liegt auch das ganze Dreieck ABC in der Ebene.

2.3

Ein Normalenvektor der $x$ - $y$ -Ebene ist $\overrightarrow{n}=\pmatrix{0\\0\\1}$ , ein Normalenvektor der Dreiecksebene ist $\overrightarrow{n_E}=\pmatrix{1\\0\\3}$ .

Damit lässt sich der Winkel zwischen den beiden Ebenen bestimmen:

$\begin{array}[t]{rll} \cos(\alpha)&= &\dfrac{\pmatrix{1\\0\\3} \circ \pmatrix{0\\0\\1}}{\left|\pmatrix{1\\0\\3} \right| \cdot \left|\pmatrix{0\\0\\1}\right|}&\quad \scriptsize \\[5pt] \cos(\alpha)&=& \dfrac{3}{\sqrt{1^2+3^2} \cdot \sqrt{1^2}}& \\[5pt] \cos(\alpha) & = & \dfrac{3}{\sqrt{10}} \quad \scriptsize \mid\; \cos(\;)^{-1} \\[5pt] \alpha& \approx& 18,43° \end{array}$

Da der Winkel größer als 17° ist, kann das Wasser gut ablaufen und das Sonnensegel erfüllt die Bedingung.

2.4

Damit die Sonnenstrahlen senkrecht auf das Sonnensegel einfallen, müssen ihre Richtungsvektoren Vielfache eines Normalenvektors der Ebene des Sonnensegels sein. Mit $A$ und dem Schattenpunkt $\(A$ lässt sich ein Richtungsvektor der Sonnenstrahlen bestimmen:

$\overrightarrow{u} = \pmatrix{-5 \\ 3 \\0} - \pmatrix{-1 \\ 1 \\ 2} = \pmatrix{-4 \\2 \\-2}$

Da $\overrightarrow{u}$ offensichtlich kein Vielfaches des Vektors $\overrightarrow{n_E}=\pmatrix{1\\0\\3}$ ist, fallen die Sonnenstrahlen nicht senkrecht auf das Sonnensegel.

Schattenpunkt $\(C$
Die Geradengleichung des Sonnentrahls, der durch $C$ verläuft, lautet:

$h:\overrightarrow{x} =\pmatrix{-4\\3\\3} +s\cdot \pmatrix{-4\\2\\-2}$

$h$ schneidet die $x$ - $y$ -Ebene, wenn die $z$ -Koordinate geich $0$ ist. Damit folgt:

$\begin{array}[t]{rll} 3-2s&=&0 &\quad \scriptsize \mid -3 \; \\[5pt] -2s&=&-3 &\quad \scriptsize \mid :(-2) \; \\[5pt] s&=& \dfrac{3}{2} &\quad \scriptsize \; \\[5pt] \end{array}$

Daraus ergibt sich der Punkt

$C‘=\pmatrix{-4\\3\\3} +\dfrac{3}{2}\cdot \pmatrix{-4\\2\\-2} =\pmatrix{-10\\6\\0}$

$C‘$ hat die Koordinaten $(-10 \mid 6 \mid 0)$ .

2.5

Mit den Punkten $P$ und $Q$ lässt sich die Gerade $g:\overrightarrow{x}=\pmatrix {-5\\3\\5} +t\cdot \pmatrix{5\\0\\-1}$ aufstellen.

Mit der Geraden $g,$ also auch mit den Koordinaten aus der Geraden $g: \pmatrix{x\\y\\z} = \pmatrix{-5+5t\\3\\5-t},$ lassen sich folglich alle Punkte des Lichtbandes darstellen.

Um nun den Punkt mit dem geringsten Abstand zu $A$ zu finden ist eine zu $g$ orthogonale Hilfsebene $H$ , auf der der Punkt $A$ liegt, notwendig.

$\overrightarrow{n_H}=\pmatrix{5\\0\\-1}$

$\begin{array}[t]{rll} 5x-z&=& d &\quad \scriptsize \mid\; \text{Punkt A einsetzen} \\[5pt] -5-2&=& d \\[5pt] -7 &=& d \end{array}$

Es gilt also $H: 5x - z = -7.$

Schnittpunkt von $g$ mit $H$ :

$\begin{array}[t]{rll} 5\cdot(-5+5t)-(5-t)&=&-7 \\[5pt] -25+25t-5+t&=&-7 \\[5pt] -30+26t&=&-7 \quad \scriptsize \mid\;+30 \\[5pt] 26t&=&23 \quad \scriptsize \mid\; :26 \\[5pt] t&=&\dfrac{23}{26} \end{array}$

Für $t=\dfrac{23}{26}$ hat der zugehörige Punkt des Lichtbandes den geringsten Abstand zum Punkt $A$ .

2.6

Definiere $F$ für ein fehlerhaftes Sonnensegel und $N$ für ein Sonnensegel aus Naturfasern.

Die Wahrscheinlichkeit, dass ein Sonnensegel fehlerhaft ist, lautet:
$P(F) = 1 - P(\overline{F}) =1 - 0,98$ $= 0,02$ $= 2 \; \%$

Die Wahrscheinlichkeit für ein fehlerhaftes Sonnensegel aus Naturfasern lautet:
$P(F \cap N) = 0,4 \cdot 0,023 = 0,0092$ $= 0,92 \; \%$

Daraus folgt die Wahrscheinlichkeit für ein fehlerhaftes Sonnensegel aus Kunstfasern:
$P(F \cap \overline{N}) = P(F) - P(F \cap N)$ $= 0,02 - 0,0092 = 0,0108 = 1, 08 \; \%$

Der prozentuale Anteil der Sonnensegel ohne Materialfehler an allen aus Naturfasern hergestellten Sonnensegeln lässt sich wie folgt berechnen:
$1 - 0,023 = 0,977 = 9,77 \; \%$

2.7

Sei $X$ die Anzahl der Sonnensegel mit Materialfehler. $X$ ist $B_{150; \; 0,02}$ verteilt mit der Null- und Alternativhypothese:

$H_0: p_0 \leq 0,02$
$H_1: p\gt 0,02$

Es handelt sich also um einen rechtsseitigen Hypothesentest.

Mit dem Signifikanzniveau $\alpha =5$ und $k = 8$ ergibt sich:

$P(X\geq 8) =1-P(X \leq 7) \approx 0,0110$ $\leq 0,05$
Damit wird die Nullhypothese abgelehnt und somit die Vermutung des Herstellers bestätigt.