Teil A

In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1

Die Funktion $f$ mit $f(x)=x^{2}-6 \cdot x+11 \quad(x \in \mathbb{R})$ besitzt die Extremstelle:

	$-3$
	$0$
	$2$
	$3$
	$11$

1.2

Die Funktion $F$ mit $F(x)=2 \cdot x \cdot \mathrm e ^{x} \quad(x \in \mathbb{R})$ ist eine Stammfunktion einer in $\mathbb{R}$ definierten Funktion $f.$

Eine weitere Stammfunktion der Funktion $f$ kann durch folgenden Term beschrieben werden:

	$2\cdot \mathrm e^x$
	$x^2\cdot \mathrm e^x$
	$x\cdot \mathrm e^x$
	$2\cdot x\cdot \mathrm e^x + 2\cdot \mathrm e^x$
	$2\cdot x\cdot \mathrm e^x +2$

1.3

Die Funktion $f$ mit $f(x)=\sin (x)+0,5 \quad(x \in \mathbb{R})$ hat den Wertebereich:

	$\{y \mid y \in \mathbb{R} ; y \leq 0,5\}$
	$\{y \mid y \in \mathbb{R} ; -0,5\leq y \leq 1,5\}$
	$\{y \mid y \in \mathbb{R} ; -0,5 \leq y \leq 0,5\}$
	$\{y \mid y \in \mathbb{R} ; -1 \leq y \leq 1\}$
	$\{y \mid y \in \mathbb{R} ; y \geq 0,5\}$

1.4

Von einer Strecke $\overline{A B}$ sind die Koordinaten des Punkts $A(1 \mid-5)$ und des Mittelpunkts $M(2 \mid-3)$ gegeben.

Der Punkt $B$ besitzt die Koordinaten:

	$(1,5\|-4)$
	$(0,5\|1)$
	$(3\|-1)$
	$(0\|-7)$
	$(-1\|3)$

1.5

Für welchen positiven Wert $r$ besitzt der zum Punkt $A(r|-4| 2)$ gehörende Ortsvektor die Länge 6?

	$r=3$
	$r=4$
	$r=16$
	$r=18$
	$r=36$

Für Aufgabe 1 erreichbare BE-Anzahl: 5

Gegeben ist die Ebene $E: 3 \cdot x-2 \cdot y=0$ .

2.1

Prüfe, ob der Punkt $(1|1,5| 7)$ in $E$ liegt.

(1 BE)

2.2

Beschreibe die besondere Lage von $E$ im Koordinatensystem.

(2 BE)

2.3

Bestimme diejenige reelle Zahl $s$ , für die die Ebene $F: 2 \cdot x+s \cdot y+z=4$ senkrecht zu $E$ steht.

(2 BE)

Gegeben sind die Punkte $A(0|0| 0), B(8|6| 0)$ und $C(4|3| z)$ , wobei $z$ eine positive reelle Zahl ist.

3.1

Zeige, dass es sich beim Dreieck $A B C$ um ein gleichschenkliges Dreieck mit der Basis $\overline{A B}$ handelt.

(2 BE)

3.2

Das Dreieck $A B C$ hat den Flächeninhalt $35 .$

Bestimme den Wert von $z$ .

(3 BE)

Betrachtet werden die Exponentialfunktionen $f$ und $g.$

4.1

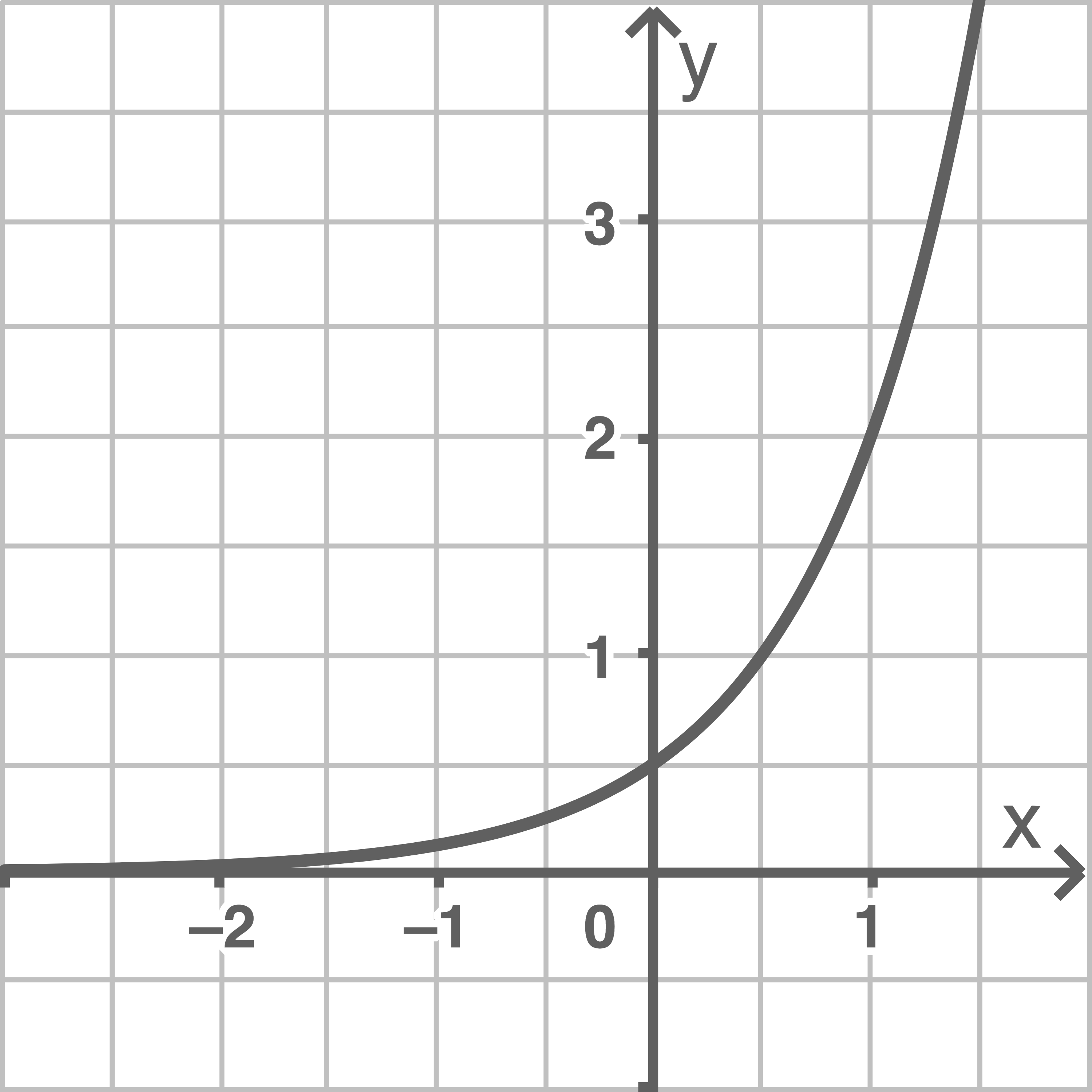
Die Abbildung zeigt den Graphen von $f$ mit $f(x)=a \cdot b^{x}$ und $a, b \in \mathbb{R}$ sowie $a>0$ und $b>0$ . Bestimme die passenden Werte von $a$ und $b$ .

(3 BE)

4.2

Der Graph der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=3^{x}$ wird um 2 in negative $x$ -Richtung verschoben.

Zeige, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von $g$ in $y$ -Richtung erzeugt werden kann.

(2 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^{2}$ .

Bestimme diejenige reelle Zahl $m$ mit $m\lt0$ , für die der Graph von $f$ und die Gerade mit der Gleichung $y=m \cdot x$ eine Fläche mit dem Inhalt 36 einschließen.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Ableitung bilden:

$\(f$

Hinreichende Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} f$

Da vorausgesetzt ist, dass eine Extremstelle existiert, kann hier auf das Prüfen der hinreichenden Bedingung verzichtet werden.

Die Funktion $f$ besitzt also eine Extremstelle bei $x=3.$

1.2

Stammfunktionen der Funktion $f$ haben die Form $2\cdot x\cdot \mathrm e^x +c.$

Somit kann eine weitere Stammfunktion der Funktion $f$ durch den Term $2\cdot x\cdot \mathrm e^x +2$ beschrieben werden.

1.3

Die Funktion $\sin (x)$ hat den Wertebereich $\{y \mid y \in \mathbb{R} ;-1 \leq y \leq 1\}.$

Da $\sin (x)$ um $+0,5$ in $y$ -Richtung verschoben wurde, hat die Funktion $f$ den Wertebereich $\{y \mid y \in \mathbb{R} ;-0,5 \leq y \leq 1,5\}.$

1.4

$\begin{array}[t]{rll} \overrightarrow{AM}&=&\pmatrix{2\\-3}-\pmatrix{1\\-5} & \\[5pt] &=&\pmatrix{1\\2} & \\[5pt] \end{array}$

$\begin{array}[t]{rll} \overrightarrow{OB}&=&\overrightarrow{OA}+ 2\cdot \overrightarrow{AM} & \\[5pt] &=&\pmatrix{1\\-5}+ 2\cdot \pmatrix{1\\2} & \\[5pt] &=&\pmatrix{3\\-1} \end{array}$

Der Punkt $B$ besitzt folglich die Koordinaten $(3 \mid -1).$

1.5

$\begin{array}[t]{rll} \left| \pmatrix{r\\-4\\2}\right|&=&6 & \\[5pt] \sqrt{r^2+(-4)^2+2^2}&=&6 & \\[5pt] \sqrt{r^2+20}&=&6 &\quad \scriptsize \mid\; ^2\\[5pt] r^2+20&=&36 &\quad \scriptsize \mid\;-20 \\[5pt] r^2&=&16 &\quad \scriptsize \mid\;\sqrt{\; } \\[5pt] r&=&\pm 4 \end{array}$

Da nach einem positiven Wert gesucht wird, muss $r=4$ gelten, sodass der zugehörige Ortsvektor die Länge $6$ besitzt.

2.1

Punktprobe durch Einsetzen der Koordinaten in $E:$

$3\cdot 1-2\cdot 1,5=3-3=0$

Also liegt der Punkt in der Ebene $E.$

2.2

Da die Koordinatengleichung unabhängig von der $z$ -Koordinate ist und Null ergibt, enthält die Ebene die $z$ -Achse.

2.3

Normalenvektoren der Ebenen sind beispielsweise $\overrightarrow{n_E}=\pmatrix{3\\-2\\0}$ und $\overrightarrow{n_F}=\pmatrix{2\\s\\1}.$

Für die Orthgonalität der beiden Ebenen muss gelten:

$\begin{array}[t]{rll} \overrightarrow{n_E} \circ \overrightarrow{n_F}&=& 0 &\\[5pt] \pmatrix{3\\-2\\0}\circ \pmatrix{2\\s\\1}&=& 0&\\[5pt] 3 \cdot 2 + -2\cdot s + 0\cdot 1&=& 0&\quad \scriptsize \mid -6\\[5pt] -2s&=& -6&\quad \scriptsize \mid :(-2)\\[5pt] s&=& 3 \end{array}$

Für $s=3$ steht die Ebene $F$ folglich senkrecht zu $E.$

3.1

Damit das Dreieck $ABC$ mit der Basis $\overline{AB}$ gleichschenklig ist, müssen die Seiten $\overline{AC}$ und $\overline{BC}$ die gleiche Länge haben.

$\begin{array}[t]{rll} |\overrightarrow{AC}|&=&\left|\pmatrix{4\\3\\z}-\pmatrix{0\\0\\0}\right|& \\[5pt] &=& \left|\pmatrix{4\\3\\z}\right|& \\[5pt] &=& \sqrt{4^2+3^2+z^2}& \\[5pt] &=& \sqrt{25+z^2} \end{array}$

$\begin{array}[t]{rll} |\overrightarrow{BC}|&=&\left|\pmatrix{4\\3\\z}-\pmatrix{8\\6\\0}\right|& \\[5pt] &=& \left|\pmatrix{-4\\-3\\z}\right|& \\[5pt] &=& \sqrt{(-4)^2+(-3)^2+z^2}& \\[5pt] &=& \sqrt{25+z^2} \end{array}$

Da beide Seitenlängen $\sqrt{25+z^2}$ betragen, ist das Dreieck gleichschenklig mit der Basis $\overline{AB}$ .

3.2

Flächeninhalt eines Dreiecks:

$A=\dfrac{1}{2}\cdot b\cdot h$

Länge der Basis $b$ berechnen

$\begin{array}[t]{rll} b&=&|\overline{AB}| & \\[5pt] &=&\left|\pmatrix{8-0\\6-0\\0-0}\right| & \\[5pt] &=&\sqrt{8^2+6^2} & \\[5pt] &=&\sqrt{100} & \\[5pt] &=&10 \end{array}$

Höhe des Dreiecks berechnen

Die Höhe des Dreiecks $ABC$ entspricht dem Abstand der Mitte $M$ der Basis $\overline{AB}$ zum Punkt $C.$

Mitte $M$ der Basis $\overline{AB}$ bestimmen:

Rechenweg anzeigen

$\overrightarrow{OM}=\pmatrix{4\\3\\0}$

$\begin{array}[t]{rll} h&=&|\overrightarrow{OC}-\overrightarrow{OM}| & \\[5pt] &=&\left| \pmatrix{4\\3\\z}- \pmatrix{4\\3\\0}\right| & \\[5pt] &=&\left| \pmatrix{0\\0\\z}\right| & \\[5pt] &=&\sqrt{z^2} & \\[5pt] &=&z \end{array}$

Wert von $z$ bestimmen

$\begin{array}[t]{rll} A&=& \dfrac{1}{2}\cdot b\cdot h& \\[5pt] 35&=& \dfrac{1}{2}\cdot 10\cdot z& \\[5pt] 35&=& 5\cdot z&\quad \scriptsize \mid\; :5\\[5pt] 7&=&z \end{array}$

Für $z=7$ besitzt das Dreieck den Flächeninhalt $35.$

4.1

Aus dem Graphen können eindeutig die Punkte $P_1(0\mid 0,5)$ und $P_2(1\mid 2)$ der Exponentialfunktion entnommen werden.

$P_1$ in $f$ einsetzen:

$\begin{array}[t]{rll} f(0)&=& 0,5 & \\[5pt] a\cdot b^0&=& 0,5 & \\[5pt] a&=& 0,5 & \\[5pt] \end{array}$

$P_2$ und $a$ in $f$ einsetzen

$\begin{array}[t]{rll} f(1)&=& 2& \\[5pt] 0,5\cdot b^1&=& 2& \quad \scriptsize \mid :0,5\\[5pt] b &=& 4 \end{array}$

Die Abbildung zeigt folglich den Graphen von $f(x)=0,5\cdot 4^x.$

4.2

Verschiebung von $g$ um $2$ in negative $x$ -Richtung:

$g_2(x)=3^{x+2}$

Anwendung der Potenzgesetze:

$3^{x+2}=3^x\cdot 3^2=3^x\cdot 9$

Der Multiplikationsfaktor $9$ streckt den Graphen von $g$ in $y$ -Richtung.

Die gesuchte Fläche wird von den Graphen der beiden Funktionen und deren Schnittstellen eingegrenzt.

1. Schritt: Bestimmung der Schnittstellen

$\begin{array}[t]{rll} f(x)&=&y \\[5pt] x^2&=&m\cdot x &\quad \scriptsize \mid\;-m\cdot x \\[5pt] x^2-m\cdot x&=&0 &\\[5pt] x \cdot (x-m)&=&0&\\[5pt] \end{array}$

Mit Hilfe des Satzes vom Nullprodukt kann die Gleichung mit $x_1=m$ und $x_2=0$ gelöst werden.

2. Schritt: Berechnung des Flächeninhalts der eingeschlossenen Fläche

$A=-\dfrac{1}{6} m^3$

Rechenweg anzeigen

3. Schritt: Bestimmung von $m$

$\begin{array}[t]{rll} A&=&36\\[5pt] -\dfrac{1}{6}m^3&=&36 &\quad \scriptsize \mid\; \cdot (-6)\\[5pt] m^3&=&-6^3 &\quad \scriptsize \mid\; \sqrt[3]{\;}\\[5pt] m&=&-6 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?