Teil A – Wahlbereich 1
4
Die Abbildung 1 zeigt den Graphen einer in 
definierten Funktion 
4.1
Skizziere in die Abbildung 1 den Graphen der ersten Ableitungsfunktion von
(3 BE)
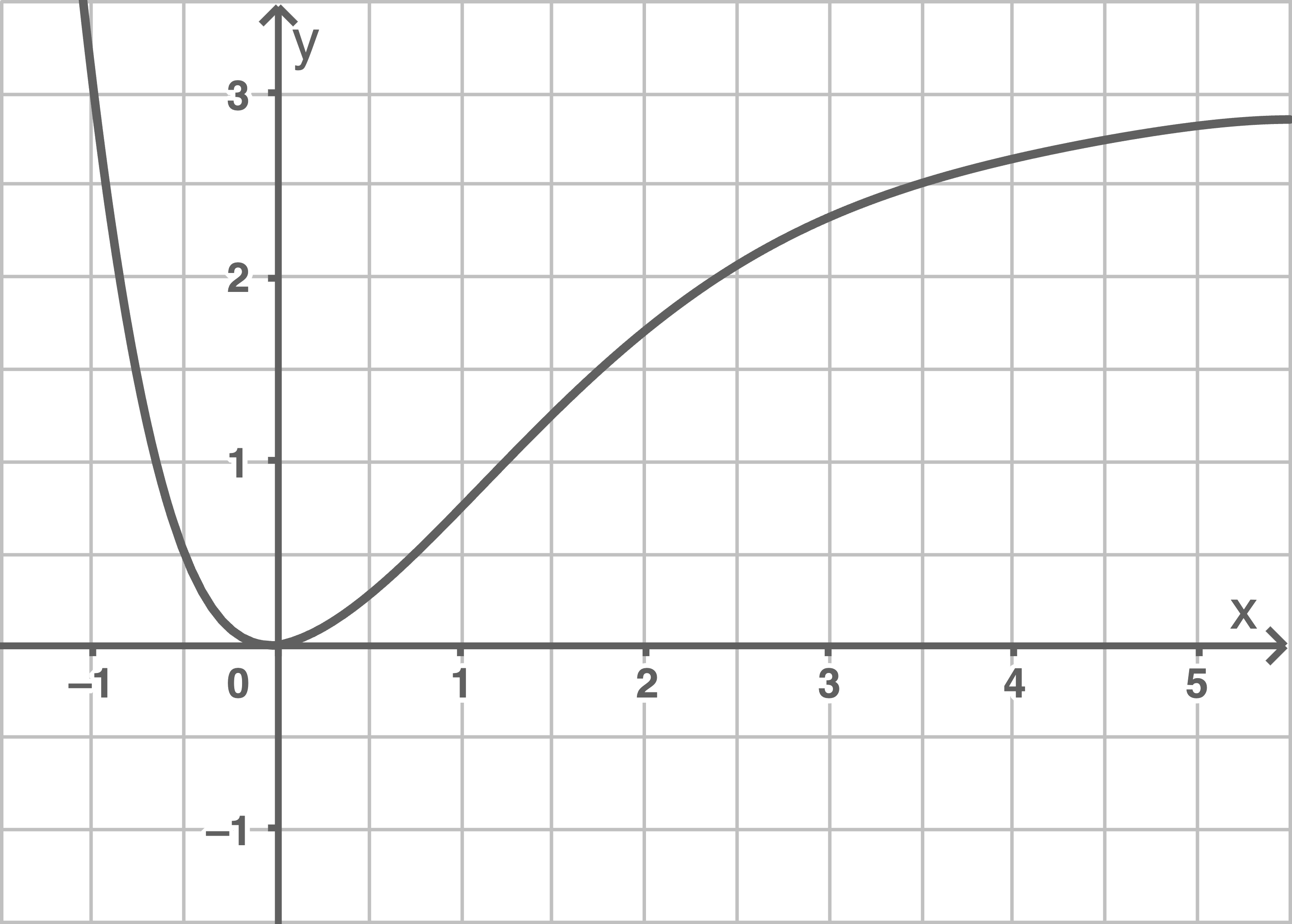
Abbildung 1
4.2
Einer der Graphen 
und 
in den folgenden Abbildungen stellt den Graphen der Funktion 
mit 
dar.
Gib den Graphen an und begründe die Angabe.
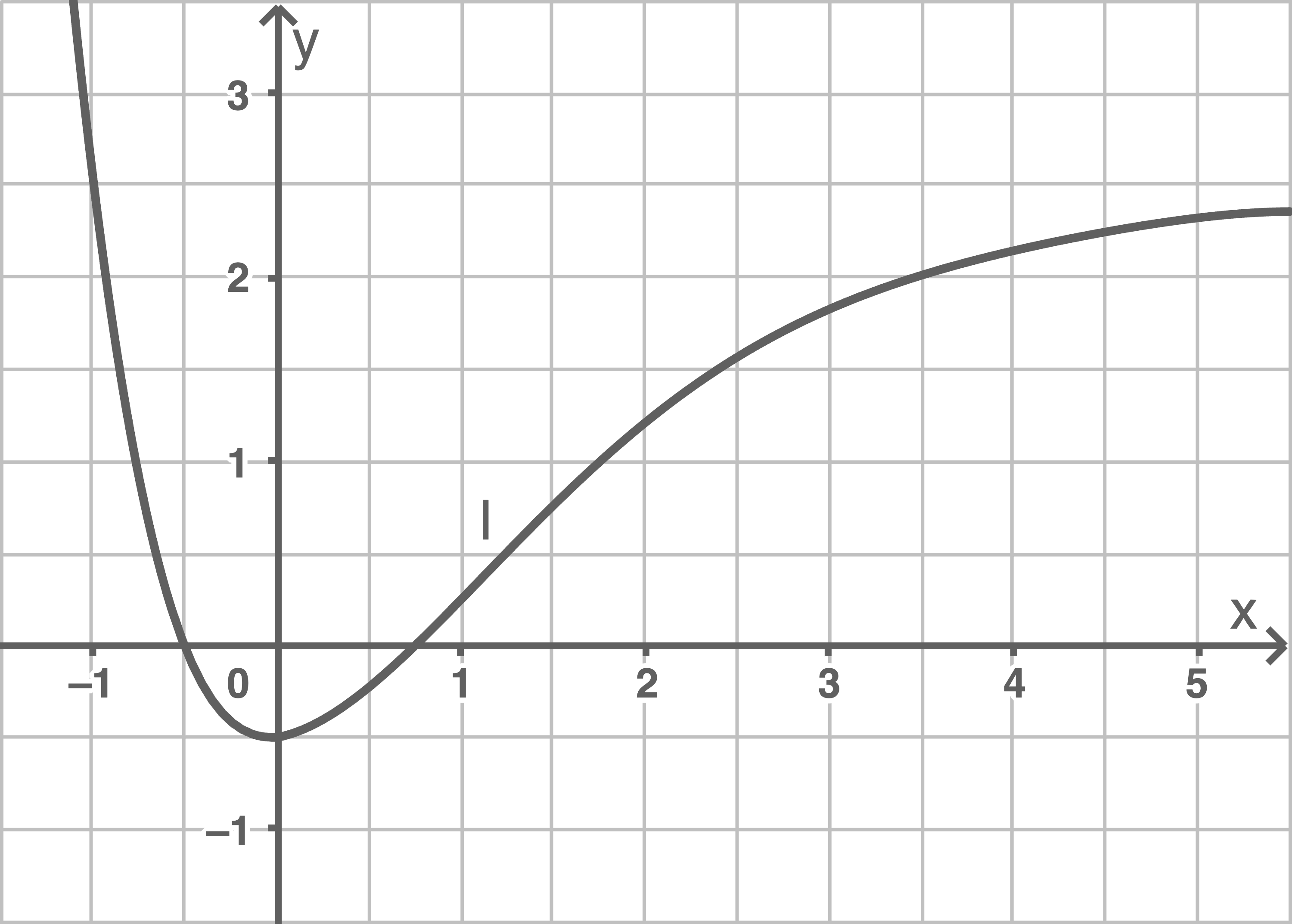
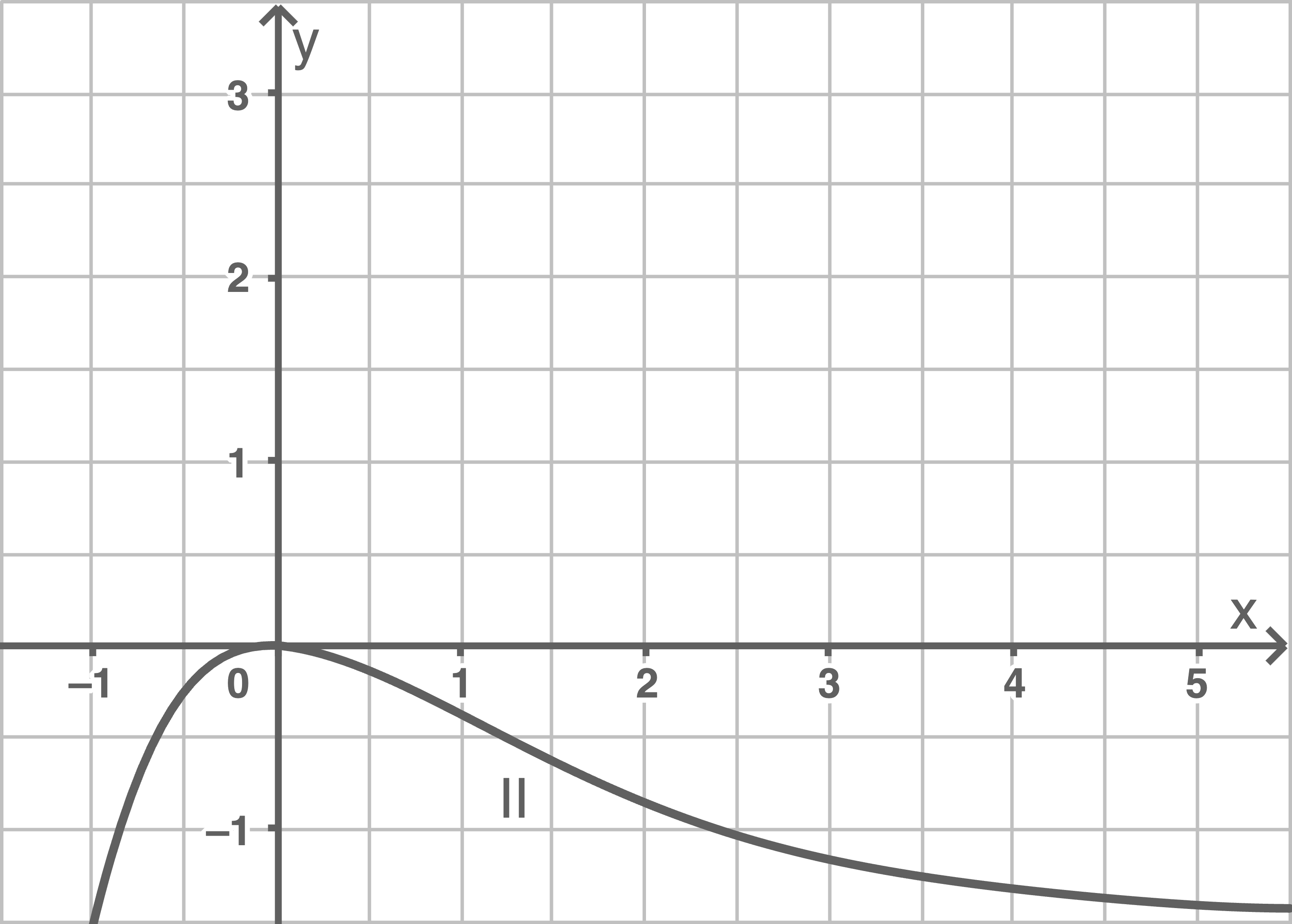
(2 BE)
5
Gegeben ist die Ebene 
5.1
Beschreibe die besondere Lage von 
im Koordinatensystem.
(2 BE)
5.2
Ermittle die Koordinațen des Schnittpunkts von und der Geraden mit 
(3 BE)
6
Ein Glücksrad besteht aus drei Sektoren, von denen einer rot, einer blau und einer grün ist.
Bei einmaligem Drehen des Glücksrads wird der rote und der blaue Sektor mit der gleichen Wahrscheinlichkeit erzielt; der blaue Sektor mit einer doppelt so großen Wahrscheinlichkeit wie der grüne Sektor.
6.1
Zeige, dass die Wahrscheinlichkeit, bei einmaligem Drehen des Glücksrads den grünen Sektor zu erzielen, 
beträgt.
(2 BE)
6.2
Das Glücksrad wird dreimal gedreht.
Berechne die Wahrscheinlichkeit für das Ereignis „Es wird mindestens einmal der grüne Sektor erzielt“.
Beschreibe ein Ereignis im gegebenen Zusammenhang, dessen Wahrscheinlichkeit mit dem Term 
berechnet werden kann.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
4.1
Die Extremstelle von 
entspricht der Nullstelle von 
Die Wendestelle von entspricht der Extremstelle von Somit ergibt sich:
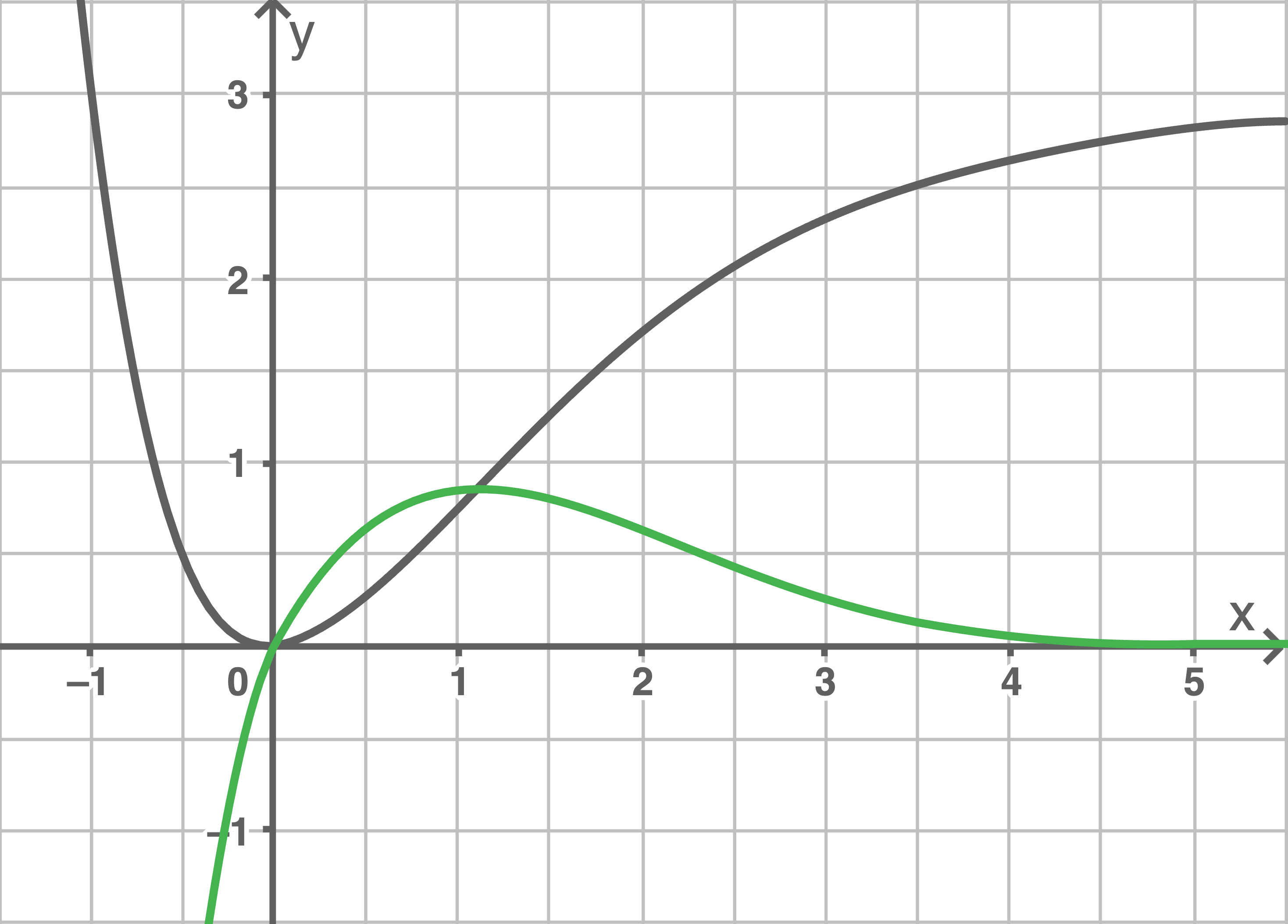
4.2
Das negative Vorzeichen des Faktors 
spiegelt den Graphen von an der 
-Achse.
Außerdem wird der Graph um den Faktor 
gestaucht und verläuft folglich flacher.
Der Graph der Funktion wird also durch den Graphen dargestellt.
5.1
Die Ebenengleichung ist unabhängig von 
Somit liegt die Ebene parallel zur 
-Achse.
5.2
Es gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{x}&=& \pmatrix{1\\1\\-1}+r\cdot \pmatrix{-5\\2\\12} &\\[5pt]
&=& \pmatrix{1-5r\\1+2r\\-1+12r}
\end{array}\)](https://mathjax.schullv.de/d018b1085b91da6eab94cd9a6cffa79177f88f553d43430f38d2fe7b84b29693?color=5a5a5a)
Einsetzen der Koordinaten in die Parametergleichung von 
![\(\begin{array}[t]{rll}
2\cdot (1-5r)+2\cdot (1+2r)&=& 1 &\\[5pt]
2-10r+2+4r&=& 1&\\[5pt]
4-6r&=& 1 &\quad \scriptsize \mid\; -4\\[5pt]
-6r&=& -3&\quad \scriptsize \mid\; :(-6)\\[5pt]
r&=& 0,5
\end{array}\)](https://mathjax.schullv.de/6c59798db4121e85bae026e6de1c671330cd7c074f10011d7d88ad77e948b596?color=5a5a5a)
Die Koordinaten des Schnittpunkts 
ergeben sich nun durch Einsetzen von 
in die Geradengleichung:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=& \pmatrix{1-5\cdot 0,5\\1+2\cdot 0,5\\-1+12\cdot 0,5} & \\[5pt]
&=& \pmatrix{-1,5 \\2\\5}
\end{array}\)](https://mathjax.schullv.de/b33a9870fa9ec2a1facb7a7c5eb76e8fae3b2a99708e7ec82608e795436ae6ff?color=5a5a5a)
6.1
6.2
Wahrscheinlichkeit berechnen
beschreibt die Anzahl der Drehungen, bei denen der grüne Sektor erzielt wird, und ist binomialverteilt mit 
und 
Mit dem Gegenereignis ergibt sich:
![\(\begin{array}[t]{rll}
P(X\geq 1)&=& 1- P(X=0) &\\[5pt]
&=& 1- \left(\dfrac{4}{5}\right)^3 &\\[5pt]
&\approx& 0,488
\end{array}\)](https://mathjax.schullv.de/c748de464ddf9ed508ae7a6a008aaef296b576be7e417abff6e8ee58fbb1332b?color=5a5a5a)
Die Wahrscheinlichkeit für das Ereignis, dass mindestens einmal der grüne Sektor erzielt wird, beträgt somit ca. 
Ereignis beschreiben
Beim dreimaligen Drehen des Glücksrads wird jede Farbe genau einmal erzielt.