Teil B2
Die Abbildung zeigt den grundsätzlichen Aufbau eines Pumpspeicherkraftwerks.
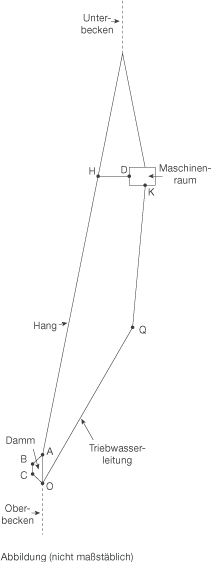 Das Oberbecken ist mit dem unterirdischen Maschinenraum durch zwei baugleiche parallel zueinander verlaufende Triebwasserleitungen verbunden. In der Abbildung ist nur eine der beiden Leitungen von
Das Oberbecken ist mit dem unterirdischen Maschinenraum durch zwei baugleiche parallel zueinander verlaufende Triebwasserleitungen verbunden. In der Abbildung ist nur eine der beiden Leitungen von  über
über  zu
zu  sichtbar.
Das Oberbecken wird auf einer Länge von
sichtbar.
Das Oberbecken wird auf einer Länge von  Metern von einem geradlinig verlaufenden Damm begrenzt. Der Damm kann als gerades Prisma betrachtet werden. Die Grundfläche
Metern von einem geradlinig verlaufenden Damm begrenzt. Der Damm kann als gerades Prisma betrachtet werden. Die Grundfläche  dieses Prismas ist ein gleichschenkliges Trapez mit einer Höhe von
dieses Prismas ist ein gleichschenkliges Trapez mit einer Höhe von  Metern. Die Längen der beiden parallelen Seiten dieses Trapezes betragen
Metern. Die Längen der beiden parallelen Seiten dieses Trapezes betragen  Meter bzw.
Meter bzw.  Meter.
Ein kartesisches Koordinatensystem (
Meter.
Ein kartesisches Koordinatensystem ( Längeneinheit entspricht
Längeneinheit entspricht  Meter) wird so festgelegt, dass der Punkt
Meter) wird so festgelegt, dass der Punkt  im Koordinatenursprung liegt.
Die Grundfläche
im Koordinatenursprung liegt.
Die Grundfläche  des Prismas liegt in der
des Prismas liegt in der  -
- -Koordinatenebene. Der Punkt
-Koordinatenebene. Der Punkt  liegt auf dem positiven Teil der
liegt auf dem positiven Teil der  -Achse.
-Achse.
 und verläuft geradlinig in Richtung des Vektors
und verläuft geradlinig in Richtung des Vektors  bis zum Punkt
bis zum Punkt  . Vom Punkt
. Vom Punkt  aus verläuft diese Triebwasserleitung geradlinig in Richtung des Vektors
aus verläuft diese Triebwasserleitung geradlinig in Richtung des Vektors  und trifft im Punkt
und trifft im Punkt  auf den Maschinenraum.
Der Punkt
auf den Maschinenraum.
Der Punkt  besitzt die Koordinaten
besitzt die Koordinaten  .
.

2.1 Gib die Koordinaten des Punktes  im festgelegten Koordinatensystem an.
im festgelegten Koordinatensystem an.
Ermittle die Größe des Winkels .
.
Ermittle die Größe des Winkels
(4P)
Eine der beiden Triebwasserleitungen beginnt im Punkt
2.2 Ermittle die Größe des Winkels, den die beiden Abschnitte  und
und  dieser Triebwasserleitung einschließen.
Bestimme die Gesamtlänge der Triebwasserleitung von
dieser Triebwasserleitung einschließen.
Bestimme die Gesamtlänge der Triebwasserleitung von  über
über  bis
bis  .
.
(5P)
2.3 Für die beiden parallel verlaufenden Triebwasserleitungen wurde jeweils eine  lange Bohrung mit
lange Bohrung mit  Durchmesser in den felsigen Untergrund getrieben. Der Felsausbruch für den Maschinenraum betrug ca.
Durchmesser in den felsigen Untergrund getrieben. Der Felsausbruch für den Maschinenraum betrug ca.  . Der Felsausbruch für die beiden Triebwasserleitungen und der Felsausbruch für den Maschinenraum wurden vollständig zum Bau des Damms verwendet.
Berechne den prozentualen Anteil des gesamten Felsausbruchs am Volumen des Damms.
. Der Felsausbruch für die beiden Triebwasserleitungen und der Felsausbruch für den Maschinenraum wurden vollständig zum Bau des Damms verwendet.
Berechne den prozentualen Anteil des gesamten Felsausbruchs am Volumen des Damms.
(5P)
2.4 Zum Anschluss an das Stromnetz existiert ein parallel zur  -Achse verlaufender Schacht
-Achse verlaufender Schacht  in den Maschinenraum. Der Punkt
in den Maschinenraum. Der Punkt  besitzt die Koordinaten
besitzt die Koordinaten  . Im Punkt
. Im Punkt  erreicht der Schacht den Hang zwischen Ober- und Unterbecken. Dieser Hang liegt in der Ebene
erreicht der Schacht den Hang zwischen Ober- und Unterbecken. Dieser Hang liegt in der Ebene  mit
mit  .
Ermittle die Koordinaten des Punktes
.
Ermittle die Koordinaten des Punktes  .
.
(2P)
Pumpspeicherkraftwerke können im Energieverbundnetz sowohl erhöhten Stromverbrauch als auch erhöhte Stromerzeugung ausgleichen.
2.5 An durchschnittlich  von
von  Tagen wird ein Pumpspeicherkraftwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet.
Bestimme die Wahrscheinlichkeit, mit der dieses Pumpspeicherkraftwerk innerhalb von
Tagen wird ein Pumpspeicherkraftwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet.
Bestimme die Wahrscheinlichkeit, mit der dieses Pumpspeicherkraftwerk innerhalb von  Tagen an höchstens
Tagen an höchstens  Tagen aus diesem Grund zugeschaltet werden muss.
Tagen aus diesem Grund zugeschaltet werden muss.
(2P)
2.6 An durchschnittlich  von
von  Tagen muss ein Pumpspeicherkraftwerk erhöhte Stromerzeugung ausgleichen. Mit einer Wahrscheinlichkeit von
Tagen muss ein Pumpspeicherkraftwerk erhöhte Stromerzeugung ausgleichen. Mit einer Wahrscheinlichkeit von  ist die Stromerzeugung an zwei aufeinanderfolgenden Tagen erhöht.
Zeige, dass die erhöhte Stromerzeugung an einem Tag von der des Vortages stochastisch abhängig ist.
ist die Stromerzeugung an zwei aufeinanderfolgenden Tagen erhöht.
Zeige, dass die erhöhte Stromerzeugung an einem Tag von der des Vortages stochastisch abhängig ist.
(2P)
2.
2.1
 Koordinaten des Punktes
Koordinaten des Punktes  angeben
Zuerst sollst du die Koordinaten des Punktes
angeben
Zuerst sollst du die Koordinaten des Punktes  angeben. In der Aufgabenstellung sind Eigenschaften des Punktes
angeben. In der Aufgabenstellung sind Eigenschaften des Punktes  gegeben.
Der Punkt
gegeben.
Der Punkt  ist eine Ecke des Trapezes
ist eine Ecke des Trapezes  mit den anderen Eckpunkten
mit den anderen Eckpunkten  ,
,  und
und  . Dabei erkennst du, dass die Strecke
. Dabei erkennst du, dass die Strecke  die längere Seite der beiden parallelen Seiten ist. Diese Seite ist
die längere Seite der beiden parallelen Seiten ist. Diese Seite ist  lang. Der Punkt
lang. Der Punkt  liegt im Koordinatenursprung. Also gilt:
liegt im Koordinatenursprung. Also gilt:
 Eine weitere Eigenschaft ist, dass der Punkt
Eine weitere Eigenschaft ist, dass der Punkt  auf dem positiven Teil der
auf dem positiven Teil der  -Achse liegt, also gilt
-Achse liegt, also gilt  . Liegt ein Punkt auf der
. Liegt ein Punkt auf der  -Achse, so sind seine
-Achse, so sind seine  - und
- und  -Koordinaten gleich Null:
-Koordinaten gleich Null:  und
und  . In die obige Gleichung eingesetzt ergibt dies:
. In die obige Gleichung eingesetzt ergibt dies:
 Somit ergeben sich für den Punkt
Somit ergeben sich für den Punkt  die Koordinaten
die Koordinaten  .
.
 Größe des Winkels
Größe des Winkels  berechnen
Hier ist es deine Aufgabe die Größe des Winkels
berechnen
Hier ist es deine Aufgabe die Größe des Winkels  zu berechnen. Dieser Winkel entspricht gerade dem Winkel zwischen den Vektoren
zu berechnen. Dieser Winkel entspricht gerade dem Winkel zwischen den Vektoren  und
und  . Mit Hilfe der Längenangaben in der Aufgabenstellung kannst du den Vektor
. Mit Hilfe der Längenangaben in der Aufgabenstellung kannst du den Vektor  bilden und damit dann den gesuchten Winkel berechnen.
1. Schritt: Vektor
bilden und damit dann den gesuchten Winkel berechnen.
1. Schritt: Vektor  bilden
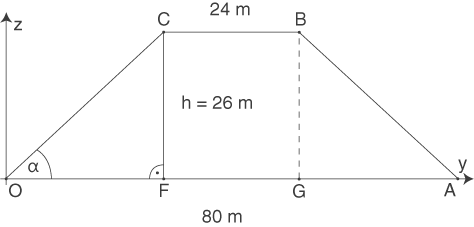
Auf der untenstehenden Skizze erkennst du die Lage des Winkels
bilden
Auf der untenstehenden Skizze erkennst du die Lage des Winkels  und der Punkte
und der Punkte  ,
,  und
und  . Die Skizze bildet das Trapez in der
. Die Skizze bildet das Trapez in der  -
- -Ebene ab:
-Ebene ab:
 Nun ist nach dem Ortsvektor des Punktes
Nun ist nach dem Ortsvektor des Punktes  gesucht. Da der Punkt
gesucht. Da der Punkt  in der
in der  -
- -Ebene liegt, ist seine
-Ebene liegt, ist seine  -Komponente gleich Null. Weiter weißt du, dass die Strecke
-Komponente gleich Null. Weiter weißt du, dass die Strecke  auf der
auf der  -Achse verläuft. Die Höhe
-Achse verläuft. Die Höhe  steht senkrecht auf der
steht senkrecht auf der  -Achse und verläuft somit parallel zur
-Achse und verläuft somit parallel zur  -Achse.
Die
-Achse.
Die  -Komponente ist dann durch die Höhe von
-Komponente ist dann durch die Höhe von  gegeben, die
gegeben, die  -Komponente durch die Länge der Strecke
-Komponente durch die Länge der Strecke  . Die Länge der Strecke
. Die Länge der Strecke  kannst du mit den angegebenen Längen der parallelen Seiten berechnen. Da es sich um ein gleichschenkliges Trapez handelt, sind die Strecken
kannst du mit den angegebenen Längen der parallelen Seiten berechnen. Da es sich um ein gleichschenkliges Trapez handelt, sind die Strecken  und
und  gleich lang, außerdem erkennst du, dass
gleich lang, außerdem erkennst du, dass  gilt. Somit kannst du die Länge der Strecke
gilt. Somit kannst du die Länge der Strecke  folgendermaßen berechnen:
folgendermaßen berechnen:
![\(\begin{array}[t]{rll}
\left|\overline{OA}\right|&=& \left|\overline{OF}\right|+\left|\overline{FG}\right|+\left|\overline{GA}\right| &\quad \scriptsize \mid\; \left|\overline{FG}\right|=\left|\overline{CB}\right| \text{ und } \left|\overline{OF}\right| = \left|\overline{GA}\right|\\[5pt]
\left|\overline{OA}\right|&=& \left|\overline{OF}\right|+\left|\overline{CB}\right|+\left|\overline{OF}\right| \\[5pt]
\left|\overline{OA}\right|&=& 2 \cdot \left|\overline{OF}\right|+\left|\overline{CB}\right| &\quad\scriptsize \mid\; -2 \cdot \left|\overline{OF}\right| -\left|\overline{OA}\right| \\[5pt]
-2 \left|\overline{OF}\right| &=& \left|\overline{CB}\right| -\left|\overline{OA}\right| &\quad\scriptsize \mid\; :(-2) \\[5pt]
\left|\overline{OF}\right| &=& \dfrac{\left|\overline{OA}\right|-\left|\overline{CB}\right|}{2} \\[5pt]
&=& \dfrac{80-24}{2} =\dfrac{56}{2}=28
\end{array}\)](https://mathjax.schullv.de/2f058d048bd8beb1e578a6cbe456e08169df064efc89e0ad287b307f90232591?color=5a5a5a) Damit ist die
Damit ist die  -Komponente
-Komponente  und der Vektor lautet:
und der Vektor lautet:
 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
Der Winkel
berechnen
Der Winkel  ist der Winkel zwischen den Vektoren
ist der Winkel zwischen den Vektoren  und
und  . Verwende also die Formel für den Schnittwinkel zweier Vektoren:
. Verwende also die Formel für den Schnittwinkel zweier Vektoren:
![\(\begin{array}[t]{rll}
\cos\left(\alpha\right)&=&\dfrac{\left| \overrightarrow{OA} \circ \overrightarrow{OC} \right|}{\left| \overrightarrow{OA} \right| \cdot \left|\overrightarrow{OC}\right|}\\[5pt]
&=&\dfrac{\left| \begin{pmatrix}0\\ 80\\ 0\end{pmatrix} \circ \begin{pmatrix}0\\ 28\\ 26\end{pmatrix} \right|}{\left| \begin{pmatrix}0\\ 80\\ 0\end{pmatrix} \right| \cdot \left|\begin{pmatrix}0\\ 28\\ 26\end{pmatrix}\right|}\\[5pt]
&=&\dfrac{\left|80 \cdot 28\right| }{\sqrt{80^2} \cdot \sqrt{28^2 +26^2}}\\[5pt]
&=&\dfrac{80 \cdot 28 }{80 \cdot \sqrt{1460}}\\[5pt]
&=&\dfrac{ 28 }{\sqrt{1460}}\\[5pt]
&\approx& 0,7328\\[5pt]
\end{array}\)](https://mathjax.schullv.de/a7b2416b204803ff75685f113c7f794547cb946f50d1d9bd69b8bccca335b300?color=5a5a5a) Für den Winkel
Für den Winkel  gilt nun:
gilt nun:
 Damit beträgt die Größe des Winkels
Damit beträgt die Größe des Winkels 
 .
.

2.2
 Größe des Winkels zwischen
Größe des Winkels zwischen  und
und  berechnen
Deine Aufgabe ist es die Größe des Winkels zwischen den Strecken
berechnen
Deine Aufgabe ist es die Größe des Winkels zwischen den Strecken  und
und  zu bestimmen. Die Strecken
zu bestimmen. Die Strecken  bzw.
bzw.  verlaufen nach Aufgabenstellung in Richtung der Vektoren
verlaufen nach Aufgabenstellung in Richtung der Vektoren  bzw.
bzw.  . Die Größe des Winkels zwischen den beiden Strecken kannst du mit Hilfe der beiden Vektoren berechnen. Betrachte dazu die untenstehende Skizze (Achtung: Dies ist eine nicht maßstabsgetreue Skizze, die Vektoren
. Die Größe des Winkels zwischen den beiden Strecken kannst du mit Hilfe der beiden Vektoren berechnen. Betrachte dazu die untenstehende Skizze (Achtung: Dies ist eine nicht maßstabsgetreue Skizze, die Vektoren  bzw.
bzw.  entsprechen nicht automatisch den Verbindungsvektoren
entsprechen nicht automatisch den Verbindungsvektoren  bzw.
bzw.  ):
):
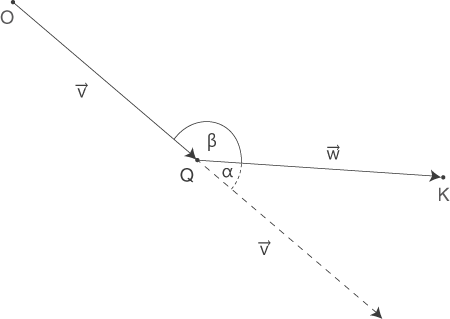 Hier ist nach dem Winkel
Hier ist nach dem Winkel  gefragt, die Vektoren
gefragt, die Vektoren  und
und  schließen den Winkel
schließen den Winkel  ein. Für die Größe der Winkel
ein. Für die Größe der Winkel  und
und  gilt:
gilt:  . Berechne also
. Berechne also  mit der Formel für den Schnittwinkel zweier Vektoren, damit kannst du dann
mit der Formel für den Schnittwinkel zweier Vektoren, damit kannst du dann  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\alpha&=& \cos^{-1}\left(\dfrac{\left|\overrightarrow{v} \circ \overrightarrow{w} \right|}{\left| \overrightarrow{v} \right| \cdot \left| \overrightarrow{w} \right|}\right) \\[5pt]
&=&\cos^{-1} \left(\dfrac{\left|\begin{pmatrix}25\\ 221\\ -128\end{pmatrix} \circ \begin{pmatrix}45\\ 398\\ -34\end{pmatrix} \right|}{\left| \begin{pmatrix}25\\ 221\\ -128\end{pmatrix} \right| \cdot \left| \begin{pmatrix}45\\ 398\\ -34\end{pmatrix}\right|} \right) \\[5pt]
&=&\cos^{-1}\left( \dfrac{\left| 25 \cdot 45 + 221 \cdot 398 + \left(-128\right) \cdot \left(-34\right)\right|}{\sqrt{25^2 + 221^2 + \left(-128\right)^2}\cdot \sqrt{45^2 + 398^2 + \left(-34\right)^2}} \right) \\[5pt]
&=&\cos^{-1}\left( \dfrac{93.435}{\sqrt{65.850}\cdot \sqrt{161.585}} \right) \\[5pt]
&\approx&\cos^{-1}\left( 0,9058\right)\\[5pt]
&\approx&25,07°\\[5pt]
\end{array}\)](https://mathjax.schullv.de/e703155b3aa2b9d1eb890b80f2b39e2250d7b67ea1067267ada7313504cb70fe?color=5a5a5a) Damit kannst du nun
Damit kannst du nun  berechnen:
berechnen:
 Die Größe des Winkels zwischen den beiden Strecken
Die Größe des Winkels zwischen den beiden Strecken  und
und  beträgt
beträgt  .
.
 Länge der Triebwasserleitung berechnen
Berechne nun die Gesamtlänge der Triebwasserleitung von
Länge der Triebwasserleitung berechnen
Berechne nun die Gesamtlänge der Triebwasserleitung von  über
über  bis
bis  . Die Länge dieser Strecke ist gerade die Länge der Verbindungsvektoren dieser Punkte. Es gilt also:
. Die Länge dieser Strecke ist gerade die Länge der Verbindungsvektoren dieser Punkte. Es gilt also:
 Die Koordinaten der Punkte
Die Koordinaten der Punkte  und
und  sind dir gegeben, du musst also noch die Koordinaten des Punktes
sind dir gegeben, du musst also noch die Koordinaten des Punktes  bestimmen.
Den Punkt
bestimmen.
Den Punkt  kannst du nun mit Hilfe der Richtungen der Wasserleitungen und den Punkten
kannst du nun mit Hilfe der Richtungen der Wasserleitungen und den Punkten  und
und  berechnen. Der Punkt
berechnen. Der Punkt  liegt sowohl auf der Geraden
liegt sowohl auf der Geraden  durch
durch  mit Richtungsvektor
mit Richtungsvektor  (erster Teil der Triebwasserleitung) als auch auf der Geraden
(erster Teil der Triebwasserleitung) als auch auf der Geraden  durch
durch  mit Richtungsvektor
mit Richtungsvektor  (zweiter Teil der Triebwasserleitung). Der Punkt
(zweiter Teil der Triebwasserleitung). Der Punkt  ist somit Schnittpunkt der Geraden
ist somit Schnittpunkt der Geraden  und
und  .
Hast du dann die Koordinaten des Punktes
.
Hast du dann die Koordinaten des Punktes  gegeben, kannst du die Verbindungsvektoren und damit die Länge des Streckenzugs berechnen.
1. Schritt: Koordinaten des Puntes
gegeben, kannst du die Verbindungsvektoren und damit die Länge des Streckenzugs berechnen.
1. Schritt: Koordinaten des Puntes  bestimmen
Stelle zuerst die Geradengleichungen von
bestimmen
Stelle zuerst die Geradengleichungen von  bzw.
bzw.  auf. Dazu sind dir jeweils ein Punkt auf der Geraden und der Richtungsvektor der Geraden gegeben. Wähle den Punkt als Stützvektor der Geraden, die Richtungsvektoren sind bereits gegeben. Dementsprechend lauten die Gleichungen der Geraden
auf. Dazu sind dir jeweils ein Punkt auf der Geraden und der Richtungsvektor der Geraden gegeben. Wähle den Punkt als Stützvektor der Geraden, die Richtungsvektoren sind bereits gegeben. Dementsprechend lauten die Gleichungen der Geraden  und
und  folgendermaßen:
folgendermaßen:
![\(\begin{array}[t]{rll}
g_1:& \overrightarrow{x}&=& \overrightarrow{OO} + s \cdot \overrightarrow{v}&\quad s \in \mathbb{R}.\\[5pt]
& \overrightarrow{x}&=& s \cdot \begin{pmatrix}25\\ 221\\ -128\end{pmatrix}&\quad s \in \mathbb{R}. \\[10pt]
g_2:& \overrightarrow{x}&=& \overrightarrow{OK} + t \cdot \overrightarrow{w}&\quad t \in \mathbb{R}. \\[5pt]
& \overrightarrow{x}&=& \begin{pmatrix}95\\ 840\\-290\end{pmatrix} + t \cdot \begin{pmatrix}45\\ 398\\ -34\end{pmatrix}&\quad t \in \mathbb{R} .\\[10pt]
\end{array}\)](https://mathjax.schullv.de/b89d2a730f95b82225e80ae76c8aea1603084d875448d62ba13d53396d823eb1?color=5a5a5a) Den Schnittpunkt dieser beiden Geraden kannst du nun mit dem Einsetzungsverfahren lösen. Setze dafür zuerst die beiden Geradengleichungen gleich, löse eine der Komponenten nach
Den Schnittpunkt dieser beiden Geraden kannst du nun mit dem Einsetzungsverfahren lösen. Setze dafür zuerst die beiden Geradengleichungen gleich, löse eine der Komponenten nach  auf, setze dies in eine weitere Komponente ein, um
auf, setze dies in eine weitere Komponente ein, um  zu berechnen, und überprüfe die beiden Werte mit der dritten Komponente.
zu berechnen, und überprüfe die beiden Werte mit der dritten Komponente.
 Aus der ersten Komponente erhältst du:
Aus der ersten Komponente erhältst du:
![\(\begin{array}[t]{rll}
s \cdot 25 &=& 95 + t \cdot 45 &\quad \scriptsize \mid\; :25\\[5pt]
s&=& \dfrac{95 + t \cdot 45}{25} \\[5pt]
s&=& 3,8 + t \cdot 1,8
\end{array}\)](https://mathjax.schullv.de/4f3346f9ce604994ed76cbb466e46bcb11af0c14d9a8643eafe955860f2b44f1?color=5a5a5a) Setze dies nun in die zweite Komponente ein:
Setze dies nun in die zweite Komponente ein:
![\(\begin{array}[t]{rll}
s \cdot 221&=&840 + t \cdot 398 &\quad \scriptsize \mid\; s \text{ einsetzen}\\[5pt]
\left( 3,8 + t \cdot 1,8\right) \cdot 221&=&840 + t \cdot 398 \\[5pt]
839,8 + t \cdot 397,8&=&840 + t \cdot 398 &\quad \scriptsize \mid\; - 839,8 -t \cdot 398 \\[5pt]
t \cdot 397,8 -t \cdot 398&=&840 -839,8\\[5pt]
- t \cdot 0,2&=&0,2 &\quad \scriptsize \mid\; \cdot \left(-5\right) \\[5pt]
t&=&-1
\end{array}\)](https://mathjax.schullv.de/6642fdbf4ba7fba83b95ba342e306a2f0cc846e5ac14320bceb5c318574cbe15?color=5a5a5a) Damit kannst du nun den Wert für
Damit kannst du nun den Wert für  berechnen:
berechnen:
 Überprüfe nun die für
Überprüfe nun die für  und
und  erhaltenen Werte in der dritten Komponente:
erhaltenen Werte in der dritten Komponente:
![\(\begin{array}[t]{rll}
s \cdot \left(-128\right)&=&-290 + t \cdot \left(-34\right) &\quad \scriptsize \mid\; s\text{ und } t \text{ einsetzen} \\[5pt]
2\cdot \left(-128\right)&=&-290 + \left(-1\right)\cdot \left(-34\right) \\[5pt]
-256&=&-290 + 34 \\[5pt]
-256&=&-256
\end{array}\)](https://mathjax.schullv.de/9e7ce75bc037bd2366f565dff9972a585c78222b176e24b4e0cc4f726b289b05?color=5a5a5a)

 Um die Koordinaten des Punktes
Um die Koordinaten des Punktes  zu bestimmen, kannst du nun
zu bestimmen, kannst du nun  in die Geradengleichung von
in die Geradengleichung von  (oder
(oder  in die Geradengleichung von
in die Geradengleichung von  einsetzen):
einsetzen):
 Damit lauten die Koordinaten des Punktes
Damit lauten die Koordinaten des Punktes 
 .
2. Schritt: Verbindungsvektoren und Länge berechnen
Der Verbindungsvektor
.
2. Schritt: Verbindungsvektoren und Länge berechnen
Der Verbindungsvektor  hast du bereits im 1. Schritt berechnet, berechne also noch den Vektor
hast du bereits im 1. Schritt berechnet, berechne also noch den Vektor  :
:
 Nun kannst du die Länge des Streckenzugs
Nun kannst du die Länge des Streckenzugs  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\left|\overline{OQK}\right|&=& \left|\overrightarrow{OQ}\right| + \left|\overrightarrow{QK}\right|& \\[5pt]
&=& \left|\begin{pmatrix}50\\ 442\\ -256\end{pmatrix}\right| + \left|\begin{pmatrix}45\\ 398\\ -34\end{pmatrix}\right| \\[5pt]
&=& \sqrt{50^2 + 442^2 + \left(-256\right)^2} + \sqrt{45^2 + 398^2 + \left(-34\right)^2}\\[5pt]
&=& \sqrt{263.400} + \sqrt{161.585}\\[5pt]
&\approx&915,20\\[5pt]
\end{array}\)](https://mathjax.schullv.de/735d05ad2285a5000bd4d9932c30e0d8de4621be8b7502b341fea4e378643fe0?color=5a5a5a) Die Gesamtlänge der Triebwasserleitung von
Die Gesamtlänge der Triebwasserleitung von  über
über  bis
bis  beträgt ca.
beträgt ca.  .
.

 Um die Koordinaten des Punktes
Um die Koordinaten des Punktes
2.3
 Prozentualen Anteil am Volumen des Damms berechnen
Berechne hier den prozentualen Anteil des gesamten Felsausbruchs am Volumen des Damms. Hierzu benötigst du das Volumen des gesamten Felsausbruchs
Prozentualen Anteil am Volumen des Damms berechnen
Berechne hier den prozentualen Anteil des gesamten Felsausbruchs am Volumen des Damms. Hierzu benötigst du das Volumen des gesamten Felsausbruchs  und das Volumen des Damms
und das Volumen des Damms  . Hast du diese beiden Größen gegeben, so berechnet sich der prozentuale Anteil
. Hast du diese beiden Größen gegeben, so berechnet sich der prozentuale Anteil  folgendermaßen:
folgendermaßen:
 Berechne also zuerst die Volumen des Felsausbruchs und des Damms.
1. Schritt: Volumen des Felsausbruchs
Der Felsausbruch besteht aus den Bohrungen für die zwei Wasserleitungen und dem Maschinenraum. Mit dem Volumen einer Wasserleitung
Berechne also zuerst die Volumen des Felsausbruchs und des Damms.
1. Schritt: Volumen des Felsausbruchs
Der Felsausbruch besteht aus den Bohrungen für die zwei Wasserleitungen und dem Maschinenraum. Mit dem Volumen einer Wasserleitung  und dem Volumen des Maschinenraums
und dem Volumen des Maschinenraums  kannst du also das Volumen des gesamten Felsausbruchs berechnen:
kannst du also das Volumen des gesamten Felsausbruchs berechnen:
 Das Volumen des Maschinenraums ist dir nach Aufgabenstellung gegeben:
Das Volumen des Maschinenraums ist dir nach Aufgabenstellung gegeben:  .
Das Volumen einer Wasserleitung kannst du mit der Länge und dem Durchmesser der Leitung berechnen. Die Leitung hat die Form eines Zylinders. Die Formel für das Volumen eines Zylinders mit Länge
.
Das Volumen einer Wasserleitung kannst du mit der Länge und dem Durchmesser der Leitung berechnen. Die Leitung hat die Form eines Zylinders. Die Formel für das Volumen eines Zylinders mit Länge  (bzw. Höhe) und Durchmesser
(bzw. Höhe) und Durchmesser  lautet:
lautet:
 Setze nun die Werte
Setze nun die Werte  und
und  ein:
ein:
![\(V_{Wasser}=915 \cdot \left(\dfrac{7}{2}\right)^2 \cdot \pi = 11.208,75 \cdot \pi \approx 35.213,33\left[\text{ m}^3\right]\)](https://mathjax.schullv.de/8cedf1061b471e8f29d3f65105d1dcc96301a845799fbd0aeb831a37cf2ec2da?color=5a5a5a) Damit kannst du nun das Volumen des Felsausbruchs berechnen:
Damit kannst du nun das Volumen des Felsausbruchs berechnen:
![\(V_{Fels}=2 \cdot 35.213,33 + 160.000 = 230.426,66 \left[\text{ m}^3\right]\)](https://mathjax.schullv.de/7ac5e249208d78e02a1f7ea526481c850adecc648a0d5c4265e786c12a083288?color=5a5a5a) 2. Schritt: Volumen des Damms berechnen
Der Damm kann als gerades Prisma betrachtet werden. Also kannst du das Volumen des Damms mit der Formel für das Volumen eines Prismas mit Länge
2. Schritt: Volumen des Damms berechnen
Der Damm kann als gerades Prisma betrachtet werden. Also kannst du das Volumen des Damms mit der Formel für das Volumen eines Prismas mit Länge  (bzw. Höhe) und Grundfläche
(bzw. Höhe) und Grundfläche  berechnen:
berechnen:
 Hier ist die Länge nach Aufgabenstellung mit
Hier ist die Länge nach Aufgabenstellung mit  gegeben. Die Grundfläche
gegeben. Die Grundfläche  ist hier der Flächeninhalt des Trapez
ist hier der Flächeninhalt des Trapez  . Berechne also zuerst den Flächeninhalt des Trapez, damit dann das Volumen des Damms.
Die Formel für den Flächeninhalt eines Trapez mit Längen
. Berechne also zuerst den Flächeninhalt des Trapez, damit dann das Volumen des Damms.
Die Formel für den Flächeninhalt eines Trapez mit Längen  und
und  der parallelen Seiten und Höhe
der parallelen Seiten und Höhe  lautet:
lautet:
 Hier sind die parallelen Seitenlängen durch
Hier sind die parallelen Seitenlängen durch  ,
,  und die Höhe durch
und die Höhe durch  gegeben. Damit kannst du die Fläche des Trapez berechnen:
gegeben. Damit kannst du die Fläche des Trapez berechnen:
![\(A_G=\dfrac{1}{2} \cdot \left(24 + 80\right) \cdot 26=\dfrac{1}{2} \cdot 104 \cdot 26 = 52 \cdot 26 = 1.352 \left[\text{ m}^2\right]\)](https://mathjax.schullv.de/f9b0435eb94519d9ca030c48babef80765dd4b9f0a65b38b74ff62d8a398051f?color=5a5a5a) Jetzt kannst du das Volumen des Damms berechnen:
Jetzt kannst du das Volumen des Damms berechnen:
![\(V_{Damm}=A_G \cdot l=1.352 \cdot 500 = 676.000 \left[\text{ m}^3\right]\)](https://mathjax.schullv.de/e7f0099960adaa2e90c5e55e95eb1045c13d6215ee4139576002ac5c64260201?color=5a5a5a) 3. Schritt: Prozentualen Anteil berechnen
Nun hast du das Volumen des Felsausbruchs und des Damms gegeben und kannst den prozentualen Anteil
3. Schritt: Prozentualen Anteil berechnen
Nun hast du das Volumen des Felsausbruchs und des Damms gegeben und kannst den prozentualen Anteil  berechnen:
berechnen:
 Der prozentuale Anteil des gesamen Felsausbruchs am Volumen des Damms beträgt ca.
Der prozentuale Anteil des gesamen Felsausbruchs am Volumen des Damms beträgt ca.  .
.
2.4
 Koordinaten des Punktes
Koordinaten des Punktes  bestimmen
Ermittle hier die Koordinaten des Punktes
bestimmen
Ermittle hier die Koordinaten des Punktes  . Nach Aufgabenstellung weißt du, dass der Punkt
. Nach Aufgabenstellung weißt du, dass der Punkt  am Schacht liegt und am Hang zwischen Ober- und Unterbecken. Den Schacht kannst du mit einer Gerade
am Schacht liegt und am Hang zwischen Ober- und Unterbecken. Den Schacht kannst du mit einer Gerade  darstellen und der Hang ist durch die Ebene
darstellen und der Hang ist durch die Ebene  gegeben. Der Punkt
gegeben. Der Punkt  ist dann der Schnittpunkt der Geraden
ist dann der Schnittpunkt der Geraden  und der Ebene
und der Ebene  .
Bestimme also zuerst eine Gleichung der Geraden
.
Bestimme also zuerst eine Gleichung der Geraden  und berechne damit den Schnittpunkt mit der Ebene
und berechne damit den Schnittpunkt mit der Ebene  .
1. Schritt: Gleichung der Gerade
.
1. Schritt: Gleichung der Gerade  aufstellen
Dir ist nach Aufgabenstellung ein Punkt auf der Geraden
aufstellen
Dir ist nach Aufgabenstellung ein Punkt auf der Geraden  und ihre Richtung gegeben. Der Punkt
und ihre Richtung gegeben. Der Punkt  befindet sich auf der Geraden und somit kann sein Ortsvektor als Stützvektor gewählt werden. Der Schacht verläuft in Richtung der
befindet sich auf der Geraden und somit kann sein Ortsvektor als Stützvektor gewählt werden. Der Schacht verläuft in Richtung der  -Achse, somit verläuft der Richtungsvektor auch in Richtung der
-Achse, somit verläuft der Richtungsvektor auch in Richtung der  -Achse:
-Achse:
![\(\begin{array}[t]{rll}
h:& \overrightarrow{x}&=& \overrightarrow{OD} + s \cdot\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}&\quad s \in \mathbb{R}.\\[5pt]
& \overrightarrow{x}&=& \begin{pmatrix}40\\ 865\\ -245\end{pmatrix} + s \cdot\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}&\quad s \in \mathbb{R}. \\[5pt]
& \overrightarrow{x}&=& \begin{pmatrix}40\\ 865\\ -245 + s\end{pmatrix}&\quad s \in \mathbb{R}. \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c2c89820bfdc7d8f786415bcd02bcf94b07262a3a5077204d86a0c09ae7981e3?color=5a5a5a) 2. Schritt: Schnittpunkt der Geraden
2. Schritt: Schnittpunkt der Geraden  und der Ebene
und der Ebene  bestimmen
Den Schnittpunkt
bestimmen
Den Schnittpunkt  kannst du nun bestimmen, indem du den allgemeinen Punkt der Geraden
kannst du nun bestimmen, indem du den allgemeinen Punkt der Geraden  in die gegebene Ebenengleichung in Koordinatenform der Ebene
in die gegebene Ebenengleichung in Koordinatenform der Ebene  einsetzt:
einsetzt:
![\(\begin{array}[t]{rll}
y+5\cdot z&=&80 &\quad \scriptsize \mid\; \text{allgemeinen Punkt einsetzen} \\[5pt]
865 + 5 \cdot \left(-245 + s\right)&=&80 \\[5pt]
865 - 1.225 + 5 \cdot s&=&80 \\[5pt]
5 \cdot s - 360 &=&80&\quad \scriptsize \mid\;+360 \\[5pt]
5 \cdot s &=&440&\quad \scriptsize \mid\;:5 \\[5pt]
s &=&88\\[5pt]
\end{array}\)](https://mathjax.schullv.de/aedda3ed6978deaf97a84ffc9c194bdcaf6e061af0b3bf0e1f99539aa2512e8d?color=5a5a5a) Setze nun den Parameter
Setze nun den Parameter  in den allgemeinen Punkt der Geraden
in den allgemeinen Punkt der Geraden  ein, um den Ortsvektor des Punktes
ein, um den Ortsvektor des Punktes  zu erhalten:
zu erhalten:
 Damit lauten die Koordinaten des Punktes
Damit lauten die Koordinaten des Punktes 
 .
.
2.5
 Untersuchen, ob die Profillinie den Blick behindert
Berechne hier die Wahrscheinlichkeit, dass an höchstens
Untersuchen, ob die Profillinie den Blick behindert
Berechne hier die Wahrscheinlichkeit, dass an höchstens  von
von  Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird.
Definiere die Zufallsvariable
Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird.
Definiere die Zufallsvariable  , die die Anzahl an Tagen unter
, die die Anzahl an Tagen unter  Tagen beschreibt, an denen der Stromverbrauch ausgeglichen werden muss. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „Stromverbrauch ausgleichen“ und „Stromverbrauch nicht ausgleichen“ gibt und durchschnittlich an
Tagen beschreibt, an denen der Stromverbrauch ausgeglichen werden muss. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „Stromverbrauch ausgleichen“ und „Stromverbrauch nicht ausgleichen“ gibt und durchschnittlich an  von
von  Tagen der Stromverbrauch ausgeglichen wird. Es gilt dementsprechend
Tagen der Stromverbrauch ausgeglichen wird. Es gilt dementsprechend  .
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als
.
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als  .
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Verwende dazu den binomcdf-Befehl deines GTR. Diesen findest du unter
.
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Verwende dazu den binomcdf-Befehl deines GTR. Diesen findest du unter
 ,
,  und
und  eingeben.
eingeben.
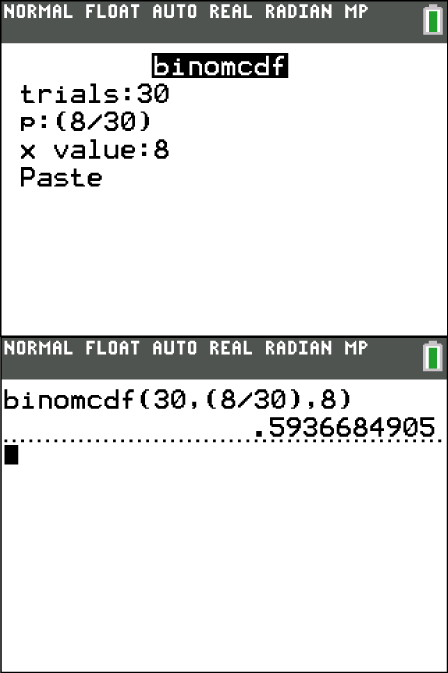 Du erhältst dann das Ergebnis
Du erhältst dann das Ergebnis  .
Die Wahrscheinlichkeit, dass an höchstens
.
Die Wahrscheinlichkeit, dass an höchstens  von
von  Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird, liegt bei
Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird, liegt bei  .
.
2ND  VARS(DISTR)
VARS(DISTR)  B: binomcdf
B: binomcdf
Du musst dann die entsprechenden Parameter 
2.6
 Unabhängigkeit zeigen
Hier ist es deine Aufgabe zu zeigen, dass die erhöhte Stromerzeugung an einem Tag von der des Vortages stochastisch abhängig ist.
Definiere zuerst die zur Aufgabe gehörigen Ereignisse:
Unabhängigkeit zeigen
Hier ist es deine Aufgabe zu zeigen, dass die erhöhte Stromerzeugung an einem Tag von der des Vortages stochastisch abhängig ist.
Definiere zuerst die zur Aufgabe gehörigen Ereignisse:
 Bestimme also die dazugehörigen Wahrscheinlichkeiten und überprüfe die Bedingung.
Die Wahrscheinlichkeiten für die Ereignisse
Bestimme also die dazugehörigen Wahrscheinlichkeiten und überprüfe die Bedingung.
Die Wahrscheinlichkeiten für die Ereignisse  und
und  sind jeweils, dass an einem Tag die Stromerzeugung erhöht ist. Diese Wahrscheinlichkeit ist durch die Aufgabenstellung mit
sind jeweils, dass an einem Tag die Stromerzeugung erhöht ist. Diese Wahrscheinlichkeit ist durch die Aufgabenstellung mit  gegeben. Die Wahrscheinlichkeit, dass an zwei aufeinander folgenden Tagen die Stromerzeugung erhöht ist, ist auch gegeben. Es gilt
gegeben. Die Wahrscheinlichkeit, dass an zwei aufeinander folgenden Tagen die Stromerzeugung erhöht ist, ist auch gegeben. Es gilt  .
Überprüfe nun die Bedingung:
.
Überprüfe nun die Bedingung:
 Damit ist die Bedingung für stochastische Abhängigkeit erfüllt. Die erhöhte Stromerzeugung an einem Tag ist von der des Vortages stochastisch abhängig.
Damit ist die Bedingung für stochastische Abhängigkeit erfüllt. Die erhöhte Stromerzeugung an einem Tag ist von der des Vortages stochastisch abhängig.
: „Die Stromerzeugung ist am Tag
erhöht“
: „Die Stromerzeugung ist am Tag
erhöht“
: „Die Stromerzeugung ist an zwei aufeinander folgenden Tagen erhöht“
2.
2.1
 Koordinaten des Punktes
Koordinaten des Punktes  angeben
Zuerst sollst du die Koordinaten des Punktes
angeben
Zuerst sollst du die Koordinaten des Punktes  angeben. In der Aufgabenstellung sind Eigenschaften des Punktes
angeben. In der Aufgabenstellung sind Eigenschaften des Punktes  gegeben.
Der Punkt
gegeben.
Der Punkt  ist eine Ecke des Trapezes
ist eine Ecke des Trapezes  mit den anderen Eckpunkten
mit den anderen Eckpunkten  ,
,  und
und  . Dabei erkennst du, dass die Strecke
. Dabei erkennst du, dass die Strecke  die längere Seite der beiden parallelen Seiten ist. Diese Seite ist
die längere Seite der beiden parallelen Seiten ist. Diese Seite ist  lang. Der Punkt
lang. Der Punkt  liegt im Koordinatenursprung. Also gilt:
liegt im Koordinatenursprung. Also gilt:
 Eine weitere Eigenschaft ist, dass der Punkt
Eine weitere Eigenschaft ist, dass der Punkt  auf dem positiven Teil der
auf dem positiven Teil der  -Achse liegt, also gilt
-Achse liegt, also gilt  . Liegt ein Punkt auf der
. Liegt ein Punkt auf der  -Achse, so sind seine
-Achse, so sind seine  - und
- und  -Koordinaten gleich Null:
-Koordinaten gleich Null:  und
und  . In die obige Gleichung eingesetzt ergibt dies:
. In die obige Gleichung eingesetzt ergibt dies:
 Somit ergeben sich für den Punkt
Somit ergeben sich für den Punkt  die Koordinaten
die Koordinaten  .
.
 Größe des Winkels
Größe des Winkels  berechnen
Hier ist es deine Aufgabe die Größe des Winkels
berechnen
Hier ist es deine Aufgabe die Größe des Winkels  zu berechnen. Dieser Winkel entspricht gerade dem Winkel zwischen den Vektoren
zu berechnen. Dieser Winkel entspricht gerade dem Winkel zwischen den Vektoren  und
und  . Mit Hilfe der Längenangaben in der Aufgabenstellung kannst du den Vektor
. Mit Hilfe der Längenangaben in der Aufgabenstellung kannst du den Vektor  bilden und damit dann den gesuchten Winkel berechnen.
1. Schritt: Vektor
bilden und damit dann den gesuchten Winkel berechnen.
1. Schritt: Vektor  bilden
Auf der untenstehenden Skizze erkennst du die Lage des Winkels
bilden
Auf der untenstehenden Skizze erkennst du die Lage des Winkels  und der Punkte
und der Punkte  ,
,  und
und  . Die Skizze bildet das Trapez in der
. Die Skizze bildet das Trapez in der  -
- -Ebene ab:
-Ebene ab:
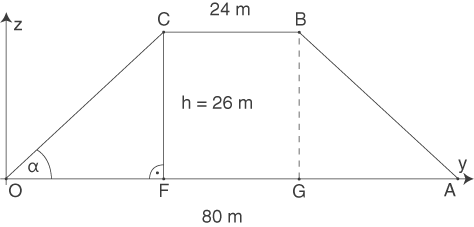 Nun ist nach dem Ortsvektor des Punktes
Nun ist nach dem Ortsvektor des Punktes  gesucht. Da der Punkt
gesucht. Da der Punkt  in der
in der  -
- -Ebene liegt, ist seine
-Ebene liegt, ist seine  -Komponente gleich Null. Weiter weißt du, dass die Strecke
-Komponente gleich Null. Weiter weißt du, dass die Strecke  auf der
auf der  -Achse verläuft. Die Höhe
-Achse verläuft. Die Höhe  steht senkrecht auf der
steht senkrecht auf der  -Achse und verläuft somit parallel zur
-Achse und verläuft somit parallel zur  -Achse.
Die
-Achse.
Die  -Komponente ist dann durch die Höhe von
-Komponente ist dann durch die Höhe von  gegeben, die
gegeben, die  -Komponente durch die Länge der Strecke
-Komponente durch die Länge der Strecke  . Die Länge der Strecke
. Die Länge der Strecke  kannst du mit den angegebenen Längen der parallelen Seiten berechnen. Da es sich um ein gleichschenkliges Trapez handelt, sind die Strecken
kannst du mit den angegebenen Längen der parallelen Seiten berechnen. Da es sich um ein gleichschenkliges Trapez handelt, sind die Strecken  und
und  gleich lang, außerdem erkennst du, dass
gleich lang, außerdem erkennst du, dass  gilt. Somit kannst du die Länge der Strecke
gilt. Somit kannst du die Länge der Strecke  folgendermaßen berechnen:
folgendermaßen berechnen:
![\(\begin{array}[t]{rll}
\left|\overline{OA}\right|&=& \left|\overline{OF}\right|+\left|\overline{FG}\right|+\left|\overline{GA}\right| &\quad \scriptsize \mid\; \left|\overline{FG}\right|=\left|\overline{CB}\right| \text{ und } \left|\overline{OF}\right| = \left|\overline{GA}\right|\\[5pt]
\left|\overline{OA}\right|&=& \left|\overline{OF}\right|+\left|\overline{CB}\right|+\left|\overline{OF}\right| \\[5pt]
\left|\overline{OA}\right|&=& 2 \cdot \left|\overline{OF}\right|+\left|\overline{CB}\right| &\quad\scriptsize \mid\; -2 \cdot \left|\overline{OF}\right| -\left|\overline{OA}\right| \\[5pt]
-2 \left|\overline{OF}\right| &=& \left|\overline{CB}\right| -\left|\overline{OA}\right| &\quad\scriptsize \mid\; :(-2) \\[5pt]
\left|\overline{OF}\right| &=& \dfrac{\left|\overline{OA}\right|-\left|\overline{CB}\right|}{2} \\[5pt]
&=& \dfrac{80-24}{2} =\dfrac{56}{2}=28
\end{array}\)](https://mathjax.schullv.de/2f058d048bd8beb1e578a6cbe456e08169df064efc89e0ad287b307f90232591?color=5a5a5a) Damit ist die
Damit ist die  -Komponente
-Komponente  und der Vektor lautet:
und der Vektor lautet:
 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
Der Winkel
berechnen
Der Winkel  ist der Winkel zwischen den Vektoren
ist der Winkel zwischen den Vektoren  und
und  . Verwende also die Formel für den Schnittwinkel zweier Vektoren:
. Verwende also die Formel für den Schnittwinkel zweier Vektoren:
![\(\begin{array}[t]{rll}
\cos\left(\alpha\right)&=&\dfrac{\left| \overrightarrow{OA} \circ \overrightarrow{OC} \right|}{\left| \overrightarrow{OA} \right| \cdot \left|\overrightarrow{OC}\right|}\\[5pt]
&=&\dfrac{\left| \begin{pmatrix}0\\ 80\\ 0\end{pmatrix} \circ \begin{pmatrix}0\\ 28\\ 26\end{pmatrix} \right|}{\left| \begin{pmatrix}0\\ 80\\ 0\end{pmatrix} \right| \cdot \left|\begin{pmatrix}0\\ 28\\ 26\end{pmatrix}\right|}\\[5pt]
&=&\dfrac{\left|80 \cdot 28\right| }{\sqrt{80^2} \cdot \sqrt{28^2 +26^2}}\\[5pt]
&=&\dfrac{80 \cdot 28 }{80 \cdot \sqrt{1460}}\\[5pt]
&=&\dfrac{ 28 }{\sqrt{1460}}\\[5pt]
&\approx& 0,7328\\[5pt]
\end{array}\)](https://mathjax.schullv.de/a7b2416b204803ff75685f113c7f794547cb946f50d1d9bd69b8bccca335b300?color=5a5a5a) Für den Winkel
Für den Winkel  gilt nun:
gilt nun:
 Damit beträgt die Größe des Winkels
Damit beträgt die Größe des Winkels 
 .
.

2.2
 Größe des Winkels zwischen
Größe des Winkels zwischen  und
und  berechnen
Deine Aufgabe ist es die Größe des Winkels zwischen den Strecken
berechnen
Deine Aufgabe ist es die Größe des Winkels zwischen den Strecken  und
und  zu bestimmen. Die Strecken
zu bestimmen. Die Strecken  bzw.
bzw.  verlaufen nach Aufgabenstellung in Richtung der Vektoren
verlaufen nach Aufgabenstellung in Richtung der Vektoren  bzw.
bzw.  . Die Größe des Winkels zwischen den beiden Strecken kannst du mit Hilfe der beiden Vektoren berechnen. Betrachte dazu die untenstehende Skizze (Achtung: Dies ist eine nicht maßstabsgetreue Skizze, die Vektoren
. Die Größe des Winkels zwischen den beiden Strecken kannst du mit Hilfe der beiden Vektoren berechnen. Betrachte dazu die untenstehende Skizze (Achtung: Dies ist eine nicht maßstabsgetreue Skizze, die Vektoren  bzw.
bzw.  entsprechen nicht automatisch den Verbindungsvektoren
entsprechen nicht automatisch den Verbindungsvektoren  bzw.
bzw.  ):
):
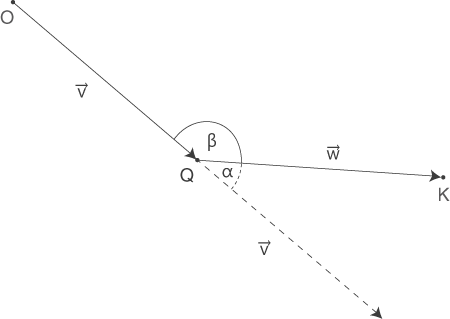 Hier ist nach dem Winkel
Hier ist nach dem Winkel  gefragt, die Vektoren
gefragt, die Vektoren  und
und  schließen den Winkel
schließen den Winkel  ein. Für die Größe der Winkel
ein. Für die Größe der Winkel  und
und  gilt:
gilt:  . Berechne also
. Berechne also  mit der Formel für den Schnittwinkel zweier Vektoren, damit kannst du dann
mit der Formel für den Schnittwinkel zweier Vektoren, damit kannst du dann  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\alpha&=& \cos^{-1}\left(\dfrac{\left|\overrightarrow{v} \circ \overrightarrow{w} \right|}{\left| \overrightarrow{v} \right| \cdot \left| \overrightarrow{w} \right|}\right) \\[5pt]
&=&\cos^{-1} \left(\dfrac{\left|\begin{pmatrix}25\\ 221\\ -128\end{pmatrix} \circ \begin{pmatrix}45\\ 398\\ -34\end{pmatrix} \right|}{\left| \begin{pmatrix}25\\ 221\\ -128\end{pmatrix} \right| \cdot \left| \begin{pmatrix}45\\ 398\\ -34\end{pmatrix}\right|} \right) \\[5pt]
&=&\cos^{-1}\left( \dfrac{\left| 25 \cdot 45 + 221 \cdot 398 + \left(-128\right) \cdot \left(-34\right)\right|}{\sqrt{25^2 + 221^2 + \left(-128\right)^2}\cdot \sqrt{45^2 + 398^2 + \left(-34\right)^2}} \right) \\[5pt]
&=&\cos^{-1}\left( \dfrac{93.435}{\sqrt{65.850}\cdot \sqrt{161.585}} \right) \\[5pt]
&\approx&\cos^{-1}\left( 0,9058\right)\\[5pt]
&\approx&25,07°\\[5pt]
\end{array}\)](https://mathjax.schullv.de/e703155b3aa2b9d1eb890b80f2b39e2250d7b67ea1067267ada7313504cb70fe?color=5a5a5a) Damit kannst du nun
Damit kannst du nun  berechnen:
berechnen:
 Die Größe des Winkels zwischen den beiden Strecken
Die Größe des Winkels zwischen den beiden Strecken  und
und  beträgt
beträgt  .
.
 Länge der Triebwasserleitung berechnen
Berechne nun die Gesamtlänge der Triebwasserleitung von
Länge der Triebwasserleitung berechnen
Berechne nun die Gesamtlänge der Triebwasserleitung von  über
über  bis
bis  . Die Länge dieser Strecke ist gerade die Länge der Verbindungsvektoren dieser Punkte. Es gilt also:
. Die Länge dieser Strecke ist gerade die Länge der Verbindungsvektoren dieser Punkte. Es gilt also:
 Die Koordinaten der Punkte
Die Koordinaten der Punkte  und
und  sind dir gegeben, du musst also noch die Koordinaten des Punktes
sind dir gegeben, du musst also noch die Koordinaten des Punktes  bestimmen.
Den Punkt
bestimmen.
Den Punkt  kannst du nun mit Hilfe der Richtungen der Wasserleitungen und den Punkten
kannst du nun mit Hilfe der Richtungen der Wasserleitungen und den Punkten  und
und  berechnen. Der Punkt
berechnen. Der Punkt  liegt sowohl auf der Geraden
liegt sowohl auf der Geraden  durch
durch  mit Richtungsvektor
mit Richtungsvektor  (erster Teil der Triebwasserleitung) als auch auf der Geraden
(erster Teil der Triebwasserleitung) als auch auf der Geraden  durch
durch  mit Richtungsvektor
mit Richtungsvektor  (zweiter Teil der Triebwasserleitung). Der Punkt
(zweiter Teil der Triebwasserleitung). Der Punkt  ist somit Schnittpunkt der Geraden
ist somit Schnittpunkt der Geraden  und
und  .
Hast du dann die Koordinaten des Punktes
.
Hast du dann die Koordinaten des Punktes  gegeben, kannst du die Verbindungsvektoren und damit die Länge des Streckenzugs berechnen.
1. Schritt: Koordinaten des Puntes
gegeben, kannst du die Verbindungsvektoren und damit die Länge des Streckenzugs berechnen.
1. Schritt: Koordinaten des Puntes  bestimmen
Stelle zuerst die Geradengleichungen von
bestimmen
Stelle zuerst die Geradengleichungen von  bzw.
bzw.  auf. Dazu sind dir jeweils ein Punkt auf der Geraden und der Richtungsvektor der Geraden gegeben. Wähle den Punkt als Stützvektor der Geraden, die Richtungsvektoren sind bereits gegeben. Dementsprechend lauten die Gleichungen der Geraden
auf. Dazu sind dir jeweils ein Punkt auf der Geraden und der Richtungsvektor der Geraden gegeben. Wähle den Punkt als Stützvektor der Geraden, die Richtungsvektoren sind bereits gegeben. Dementsprechend lauten die Gleichungen der Geraden  und
und  folgendermaßen:
folgendermaßen:
![\(\begin{array}[t]{rll}
g_1:& \overrightarrow{x}&=& \overrightarrow{OO} + s \cdot \overrightarrow{v}&\quad s \in \mathbb{R}.\\[5pt]
& \overrightarrow{x}&=& s \cdot \begin{pmatrix}25\\ 221\\ -128\end{pmatrix}&\quad s \in \mathbb{R}. \\[10pt]
g_2:& \overrightarrow{x}&=& \overrightarrow{OK} + t \cdot \overrightarrow{w}&\quad t \in \mathbb{R}. \\[5pt]
& \overrightarrow{x}&=& \begin{pmatrix}95\\ 840\\-290\end{pmatrix} + t \cdot \begin{pmatrix}45\\ 398\\ -34\end{pmatrix}&\quad t \in \mathbb{R} .\\[10pt]
\end{array}\)](https://mathjax.schullv.de/b89d2a730f95b82225e80ae76c8aea1603084d875448d62ba13d53396d823eb1?color=5a5a5a) Den Schnittpunkt dieser beiden Geraden kannst du nun mit dem Einsetzungsverfahren lösen. Setze dafür zuerst die beiden Geradengleichungen gleich, löse eine der Komponenten nach
Den Schnittpunkt dieser beiden Geraden kannst du nun mit dem Einsetzungsverfahren lösen. Setze dafür zuerst die beiden Geradengleichungen gleich, löse eine der Komponenten nach  auf, setze dies in eine weitere Komponente ein, um
auf, setze dies in eine weitere Komponente ein, um  zu berechnen, und überprüfe die beiden Werte mit der dritten Komponente.
zu berechnen, und überprüfe die beiden Werte mit der dritten Komponente.
 Aus der ersten Komponente erhältst du:
Aus der ersten Komponente erhältst du:
![\(\begin{array}[t]{rll}
s \cdot 25 &=& 95 + t \cdot 45 &\quad \scriptsize \mid\; :25\\[5pt]
s&=& \dfrac{95 + t \cdot 45}{25} \\[5pt]
s&=& 3,8 + t \cdot 1,8
\end{array}\)](https://mathjax.schullv.de/4f3346f9ce604994ed76cbb466e46bcb11af0c14d9a8643eafe955860f2b44f1?color=5a5a5a) Setze dies nun in die zweite Komponente ein:
Setze dies nun in die zweite Komponente ein:
![\(\begin{array}[t]{rll}
s \cdot 221&=&840 + t \cdot 398 &\quad \scriptsize \mid\; s \text{ einsetzen}\\[5pt]
\left( 3,8 + t \cdot 1,8\right) \cdot 221&=&840 + t \cdot 398 \\[5pt]
839,8 + t \cdot 397,8&=&840 + t \cdot 398 &\quad \scriptsize \mid\; - 839,8 -t \cdot 398 \\[5pt]
t \cdot 397,8 -t \cdot 398&=&840 -839,8\\[5pt]
- t \cdot 0,2&=&0,2 &\quad \scriptsize \mid\; \cdot \left(-5\right) \\[5pt]
t&=&-1
\end{array}\)](https://mathjax.schullv.de/6642fdbf4ba7fba83b95ba342e306a2f0cc846e5ac14320bceb5c318574cbe15?color=5a5a5a) Damit kannst du nun den Wert für
Damit kannst du nun den Wert für  berechnen:
berechnen:
 Überprüfe nun die für
Überprüfe nun die für  und
und  erhaltenen Werte in der dritten Komponente:
erhaltenen Werte in der dritten Komponente:
![\(\begin{array}[t]{rll}
s \cdot \left(-128\right)&=&-290 + t \cdot \left(-34\right) &\quad \scriptsize \mid\; s\text{ und } t \text{ einsetzen} \\[5pt]
2\cdot \left(-128\right)&=&-290 + \left(-1\right)\cdot \left(-34\right) \\[5pt]
-256&=&-290 + 34 \\[5pt]
-256&=&-256
\end{array}\)](https://mathjax.schullv.de/9e7ce75bc037bd2366f565dff9972a585c78222b176e24b4e0cc4f726b289b05?color=5a5a5a)

 Um die Koordinaten des Punktes
Um die Koordinaten des Punktes  zu bestimmen, kannst du nun
zu bestimmen, kannst du nun  in die Geradengleichung von
in die Geradengleichung von  (oder
(oder  in die Geradengleichung von
in die Geradengleichung von  einsetzen):
einsetzen):
 Damit lauten die Koordinaten des Punktes
Damit lauten die Koordinaten des Punktes 
 .
2. Schritt: Verbindungsvektoren und Länge berechnen
Der Verbindungsvektor
.
2. Schritt: Verbindungsvektoren und Länge berechnen
Der Verbindungsvektor  hast du bereits im 1. Schritt berechnet, berechne also noch den Vektor
hast du bereits im 1. Schritt berechnet, berechne also noch den Vektor  :
:
 Nun kannst du die Länge des Streckenzugs
Nun kannst du die Länge des Streckenzugs  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\left|\overline{OQK}\right|&=& \left|\overrightarrow{OQ}\right| + \left|\overrightarrow{QK}\right|& \\[5pt]
&=& \left|\begin{pmatrix}50\\ 442\\ -256\end{pmatrix}\right| + \left|\begin{pmatrix}45\\ 398\\ -34\end{pmatrix}\right| \\[5pt]
&=& \sqrt{50^2 + 442^2 + \left(-256\right)^2} + \sqrt{45^2 + 398^2 + \left(-34\right)^2}\\[5pt]
&=& \sqrt{263.400} + \sqrt{161.585}\\[5pt]
&\approx&915,20\\[5pt]
\end{array}\)](https://mathjax.schullv.de/735d05ad2285a5000bd4d9932c30e0d8de4621be8b7502b341fea4e378643fe0?color=5a5a5a) Die Gesamtlänge der Triebwasserleitung von
Die Gesamtlänge der Triebwasserleitung von  über
über  bis
bis  beträgt ca.
beträgt ca.  .
.

 Um die Koordinaten des Punktes
Um die Koordinaten des Punktes
2.3
 Prozentualen Anteil am Volumen des Damms berechnen
Berechne hier den prozentualen Anteil des gesamten Felsausbruchs am Volumen des Damms. Hierzu benötigst du das Volumen des gesamten Felsausbruchs
Prozentualen Anteil am Volumen des Damms berechnen
Berechne hier den prozentualen Anteil des gesamten Felsausbruchs am Volumen des Damms. Hierzu benötigst du das Volumen des gesamten Felsausbruchs  und das Volumen des Damms
und das Volumen des Damms  . Hast du diese beiden Größen gegeben, so berechnet sich der prozentuale Anteil
. Hast du diese beiden Größen gegeben, so berechnet sich der prozentuale Anteil  folgendermaßen:
folgendermaßen:
 Berechne also zuerst die Volumen des Felsausbruchs und des Damms.
1. Schritt: Volumen des Felsausbruchs
Der Felsausbruch besteht aus den Bohrungen für die zwei Wasserleitungen und dem Maschinenraum. Mit dem Volumen einer Wasserleitung
Berechne also zuerst die Volumen des Felsausbruchs und des Damms.
1. Schritt: Volumen des Felsausbruchs
Der Felsausbruch besteht aus den Bohrungen für die zwei Wasserleitungen und dem Maschinenraum. Mit dem Volumen einer Wasserleitung  und dem Volumen des Maschinenraums
und dem Volumen des Maschinenraums  kannst du also das Volumen des gesamten Felsausbruchs berechnen:
kannst du also das Volumen des gesamten Felsausbruchs berechnen:
 Das Volumen des Maschinenraums ist dir nach Aufgabenstellung gegeben:
Das Volumen des Maschinenraums ist dir nach Aufgabenstellung gegeben:  .
Das Volumen einer Wasserleitung kannst du mit der Länge und dem Durchmesser der Leitung berechnen. Die Leitung hat die Form eines Zylinders. Die Formel für das Volumen eines Zylinders mit Länge
.
Das Volumen einer Wasserleitung kannst du mit der Länge und dem Durchmesser der Leitung berechnen. Die Leitung hat die Form eines Zylinders. Die Formel für das Volumen eines Zylinders mit Länge  (bzw. Höhe) und Durchmesser
(bzw. Höhe) und Durchmesser  lautet:
lautet:
 Setze nun die Werte
Setze nun die Werte  und
und  ein:
ein:
![\(V_{Wasser}=915 \cdot \left(\dfrac{7}{2}\right)^2 \cdot \pi = 11.208,75 \cdot \pi \approx 35.213,33\left[\text{ m}^3\right]\)](https://mathjax.schullv.de/8cedf1061b471e8f29d3f65105d1dcc96301a845799fbd0aeb831a37cf2ec2da?color=5a5a5a) Damit kannst du nun das Volumen des Felsausbruchs berechnen:
Damit kannst du nun das Volumen des Felsausbruchs berechnen:
![\(V_{Fels}=2 \cdot 35.213,33 + 160.000 = 230.426,66 \left[\text{ m}^3\right]\)](https://mathjax.schullv.de/7ac5e249208d78e02a1f7ea526481c850adecc648a0d5c4265e786c12a083288?color=5a5a5a) 2. Schritt: Volumen des Damms berechnen
Der Damm kann als gerades Prisma betrachtet werden. Also kannst du das Volumen des Damms mit der Formel für das Volumen eines Prismas mit Länge
2. Schritt: Volumen des Damms berechnen
Der Damm kann als gerades Prisma betrachtet werden. Also kannst du das Volumen des Damms mit der Formel für das Volumen eines Prismas mit Länge  (bzw. Höhe) und Grundfläche
(bzw. Höhe) und Grundfläche  berechnen:
berechnen:
 Hier ist die Länge nach Aufgabenstellung mit
Hier ist die Länge nach Aufgabenstellung mit  gegeben. Die Grundfläche
gegeben. Die Grundfläche  ist hier der Flächeninhalt des Trapez
ist hier der Flächeninhalt des Trapez  . Berechne also zuerst den Flächeninhalt des Trapez, damit dann das Volumen des Damms.
Die Formel für den Flächeninhalt eines Trapez mit Längen
. Berechne also zuerst den Flächeninhalt des Trapez, damit dann das Volumen des Damms.
Die Formel für den Flächeninhalt eines Trapez mit Längen  und
und  der parallelen Seiten und Höhe
der parallelen Seiten und Höhe  lautet:
lautet:
 Hier sind die parallelen Seitenlängen durch
Hier sind die parallelen Seitenlängen durch  ,
,  und die Höhe durch
und die Höhe durch  gegeben. Damit kannst du die Fläche des Trapez berechnen:
gegeben. Damit kannst du die Fläche des Trapez berechnen:
![\(A_G=\dfrac{1}{2} \cdot \left(24 + 80\right) \cdot 26=\dfrac{1}{2} \cdot 104 \cdot 26 = 52 \cdot 26 = 1.352 \left[\text{ m}^2\right]\)](https://mathjax.schullv.de/f9b0435eb94519d9ca030c48babef80765dd4b9f0a65b38b74ff62d8a398051f?color=5a5a5a) Jetzt kannst du das Volumen des Damms berechnen:
Jetzt kannst du das Volumen des Damms berechnen:
![\(V_{Damm}=A_G \cdot l=1.352 \cdot 500 = 676.000 \left[\text{ m}^3\right]\)](https://mathjax.schullv.de/e7f0099960adaa2e90c5e55e95eb1045c13d6215ee4139576002ac5c64260201?color=5a5a5a) 3. Schritt: Prozentualen Anteil berechnen
Nun hast du das Volumen des Felsausbruchs und des Damms gegeben und kannst den prozentualen Anteil
3. Schritt: Prozentualen Anteil berechnen
Nun hast du das Volumen des Felsausbruchs und des Damms gegeben und kannst den prozentualen Anteil  berechnen:
berechnen:
 Der prozentuale Anteil des gesamen Felsausbruchs am Volumen des Damms beträgt ca.
Der prozentuale Anteil des gesamen Felsausbruchs am Volumen des Damms beträgt ca.  .
.
2.4
 Koordinaten des Punktes
Koordinaten des Punktes  bestimmen
Ermittle hier die Koordinaten des Punktes
bestimmen
Ermittle hier die Koordinaten des Punktes  . Nach Aufgabenstellung weißt du, dass der Punkt
. Nach Aufgabenstellung weißt du, dass der Punkt  am Schacht liegt und am Hang zwischen Ober- und Unterbecken. Den Schacht kannst du mit einer Gerade
am Schacht liegt und am Hang zwischen Ober- und Unterbecken. Den Schacht kannst du mit einer Gerade  darstellen und der Hang ist durch die Ebene
darstellen und der Hang ist durch die Ebene  gegeben. Der Punkt
gegeben. Der Punkt  ist dann der Schnittpunkt der Geraden
ist dann der Schnittpunkt der Geraden  und der Ebene
und der Ebene  .
Bestimme also zuerst eine Gleichung der Geraden
.
Bestimme also zuerst eine Gleichung der Geraden  und berechne damit den Schnittpunkt mit der Ebene
und berechne damit den Schnittpunkt mit der Ebene  .
1. Schritt: Gleichung der Gerade
.
1. Schritt: Gleichung der Gerade  aufstellen
Dir ist nach Aufgabenstellung ein Punkt auf der Geraden
aufstellen
Dir ist nach Aufgabenstellung ein Punkt auf der Geraden  und ihre Richtung gegeben. Der Punkt
und ihre Richtung gegeben. Der Punkt  befindet sich auf der Geraden und somit kann sein Ortsvektor als Stützvektor gewählt werden. Der Schacht verläuft in Richtung der
befindet sich auf der Geraden und somit kann sein Ortsvektor als Stützvektor gewählt werden. Der Schacht verläuft in Richtung der  -Achse, somit verläuft der Richtungsvektor auch in Richtung der
-Achse, somit verläuft der Richtungsvektor auch in Richtung der  -Achse:
-Achse:
![\(\begin{array}[t]{rll}
h:& \overrightarrow{x}&=& \overrightarrow{OD} + s \cdot\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}&\quad s \in \mathbb{R}.\\[5pt]
& \overrightarrow{x}&=& \begin{pmatrix}40\\ 865\\ -245\end{pmatrix} + s \cdot\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}&\quad s \in \mathbb{R}. \\[5pt]
& \overrightarrow{x}&=& \begin{pmatrix}40\\ 865\\ -245 + s\end{pmatrix}&\quad s \in \mathbb{R}. \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c2c89820bfdc7d8f786415bcd02bcf94b07262a3a5077204d86a0c09ae7981e3?color=5a5a5a) 2. Schritt: Schnittpunkt der Geraden
2. Schritt: Schnittpunkt der Geraden  und der Ebene
und der Ebene  bestimmen
Den Schnittpunkt
bestimmen
Den Schnittpunkt  kannst du nun bestimmen, indem du den allgemeinen Punkt der Geraden
kannst du nun bestimmen, indem du den allgemeinen Punkt der Geraden  in die gegebene Ebenengleichung in Koordinatenform der Ebene
in die gegebene Ebenengleichung in Koordinatenform der Ebene  einsetzt:
einsetzt:
![\(\begin{array}[t]{rll}
y+5\cdot z&=&80 &\quad \scriptsize \mid\; \text{allgemeinen Punkt einsetzen} \\[5pt]
865 + 5 \cdot \left(-245 + s\right)&=&80 \\[5pt]
865 - 1.225 + 5 \cdot s&=&80 \\[5pt]
5 \cdot s - 360 &=&80&\quad \scriptsize \mid\;+360 \\[5pt]
5 \cdot s &=&440&\quad \scriptsize \mid\;:5 \\[5pt]
s &=&88\\[5pt]
\end{array}\)](https://mathjax.schullv.de/aedda3ed6978deaf97a84ffc9c194bdcaf6e061af0b3bf0e1f99539aa2512e8d?color=5a5a5a) Setze nun den Parameter
Setze nun den Parameter  in den allgemeinen Punkt der Geraden
in den allgemeinen Punkt der Geraden  ein, um den Ortsvektor des Punktes
ein, um den Ortsvektor des Punktes  zu erhalten:
zu erhalten:
 Damit lauten die Koordinaten des Punktes
Damit lauten die Koordinaten des Punktes 
 .
.
2.5
 Untersuchen, ob die Profillinie den Blick behindert
Berechne hier die Wahrscheinlichkeit, dass an höchstens
Untersuchen, ob die Profillinie den Blick behindert
Berechne hier die Wahrscheinlichkeit, dass an höchstens  von
von  Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird.
Definiere die Zufallsvariable
Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird.
Definiere die Zufallsvariable  , die die Anzahl an Tagen unter
, die die Anzahl an Tagen unter  Tagen beschreibt, an denen der Stromverbrauch ausgeglichen werden muss. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „Stromverbrauch ausgleichen“ und „Stromverbrauch nicht ausgleichen“ gibt und durchschnittlich an
Tagen beschreibt, an denen der Stromverbrauch ausgeglichen werden muss. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „Stromverbrauch ausgleichen“ und „Stromverbrauch nicht ausgleichen“ gibt und durchschnittlich an  von
von  Tagen der Stromverbrauch ausgeglichen wird. Es gilt dementsprechend
Tagen der Stromverbrauch ausgeglichen wird. Es gilt dementsprechend  .
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als
.
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als  .
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Du kannst den binomcdf-Befehl deines GTR verwenden. Diesen findest du im STAT-Menü unter
.
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Du kannst den binomcdf-Befehl deines GTR verwenden. Diesen findest du im STAT-Menü unter
 ,
,  und
und  eingeben:
eingeben:
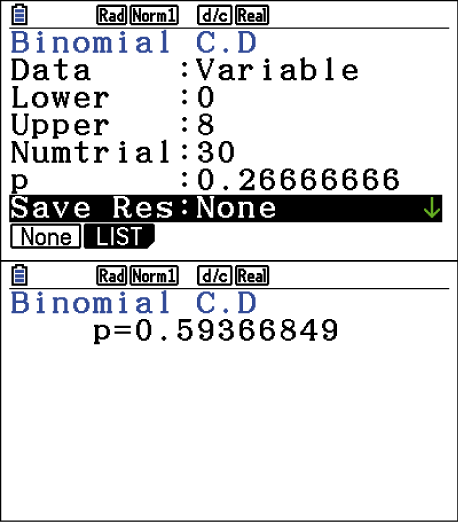 Du erhältst dann das Ergebnis
Du erhältst dann das Ergebnis  .
Die Wahrscheinlichkeit, dass an höchstens
.
Die Wahrscheinlichkeit, dass an höchstens  von
von  Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird, liegt bei
Tagen ein Pumpspeicherwerk zum Ausgleich von erhöhtem Stromverbrauch zugeschaltet wird, liegt bei  .
.
F5: DIST  F5: BINOMIAL
F5: BINOMIAL  F2: Bcd
F2: Bcd  F2: Var
F2: Var
Du musst dann die entsprechenden Parameter 
2.6
 Unabhängigkeit zeigen
Hier ist es deine Aufgabe zu zeigen, dass die erhöhte Stromerzeugung an einem Tag von der des Vortages stochastisch abhängig ist.
Definiere zuerst die zur Aufgabe gehörigen Ereignisse:
Unabhängigkeit zeigen
Hier ist es deine Aufgabe zu zeigen, dass die erhöhte Stromerzeugung an einem Tag von der des Vortages stochastisch abhängig ist.
Definiere zuerst die zur Aufgabe gehörigen Ereignisse:
 Bestimme also die dazugehörigen Wahrscheinlichkeiten und überprüfe die Bedingung.
Die Wahrscheinlichkeiten für die Ereignisse
Bestimme also die dazugehörigen Wahrscheinlichkeiten und überprüfe die Bedingung.
Die Wahrscheinlichkeiten für die Ereignisse  und
und  sind jeweils, dass an einem Tag die Stromerzeugung erhöht ist. Diese Wahrscheinlichkeit ist durch die Aufgabenstellung mit
sind jeweils, dass an einem Tag die Stromerzeugung erhöht ist. Diese Wahrscheinlichkeit ist durch die Aufgabenstellung mit  gegeben. Die Wahrscheinlichkeit, dass an zwei aufeinander folgenden Tagen die Stromerzeugung erhöht ist, ist auch gegeben. Es gilt
gegeben. Die Wahrscheinlichkeit, dass an zwei aufeinander folgenden Tagen die Stromerzeugung erhöht ist, ist auch gegeben. Es gilt  .
Überprüfe nun die Bedingung:
.
Überprüfe nun die Bedingung:
 Damit ist die Bedingung für stochastische Abhängigkeit erfüllt. Die erhöhte Stromerzeugung an einem Tag ist von der des Vortages stochastisch abhängig.
Damit ist die Bedingung für stochastische Abhängigkeit erfüllt. Die erhöhte Stromerzeugung an einem Tag ist von der des Vortages stochastisch abhängig.
: „Die Stromerzeugung ist am Tag
erhöht“
: „Die Stromerzeugung ist am Tag
erhöht“
: „Die Stromerzeugung ist an zwei aufeinander folgenden Tagen erhöht“