Teil A – Wahlbereich 2

Für jede positive reelle Zahl $a$ sind der Graph der Funktion $f_a$ mit $f_a(x)=a \cdot x^2 \quad(x \in \mathbb{R}) \quad$ und das achsenparallele Rechteck $A B C_a D_a$ mit $A(0 \mid 0)$ und $C_a\left(4 \mid f_a(4)\right)$ gegeben.

Für jedes $a$ zerlegt der Graph von $f_a$ das zugehörige Rechteck in die Teilflächen $T_1$ und $T_2.$ Die Abbildung zeigt den Sachverhalt für einen Wert von $a.$

Weise nach, dass das Verhältnis der Flächeninhalte der beiden Teilflächen unabhängig von $a$ ist.

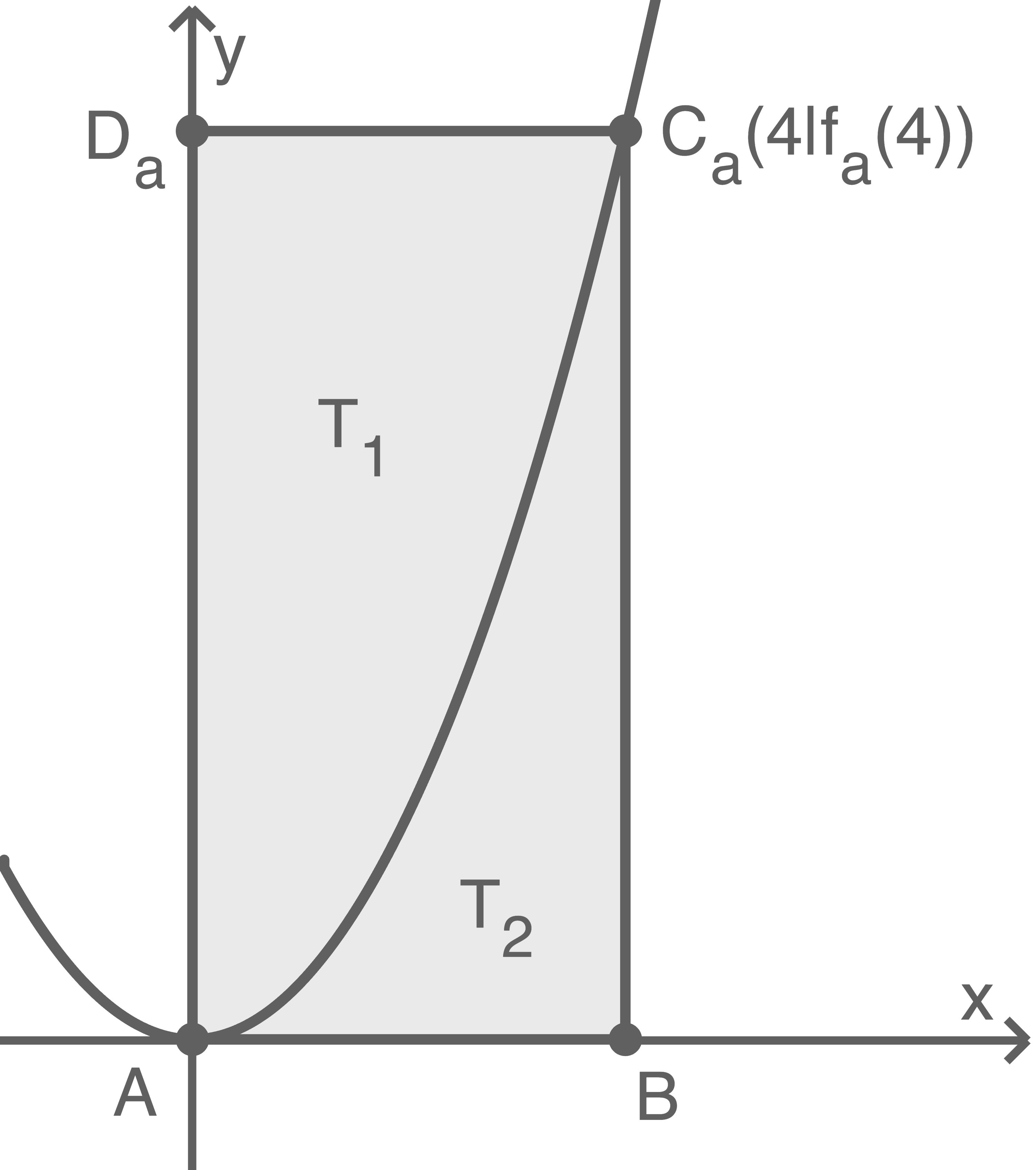
Teilflaechen Verhaeltnis Sachsen Mathe Abi 2024

(5 BE)

Gegeben sind die Punkte $A(0\mid 1\mid 1),$ $B(0\mid 5\mid 1)$ und $C(0\mid 4\mid 3).$

8.1

Begründe, dass $A, B$ und $C$ in derselben Koordinatenebene liegen.

Gib den Abstand von $C$ zur $xy$ -Ebene an.

(2 BE)

8.2

Bestimme die Koordinaten eines Punkts $D,$ so dass das Viereck $A B C D$ ein Trapez mit dem Flächeninhalt 7 ist.

(3 BE)

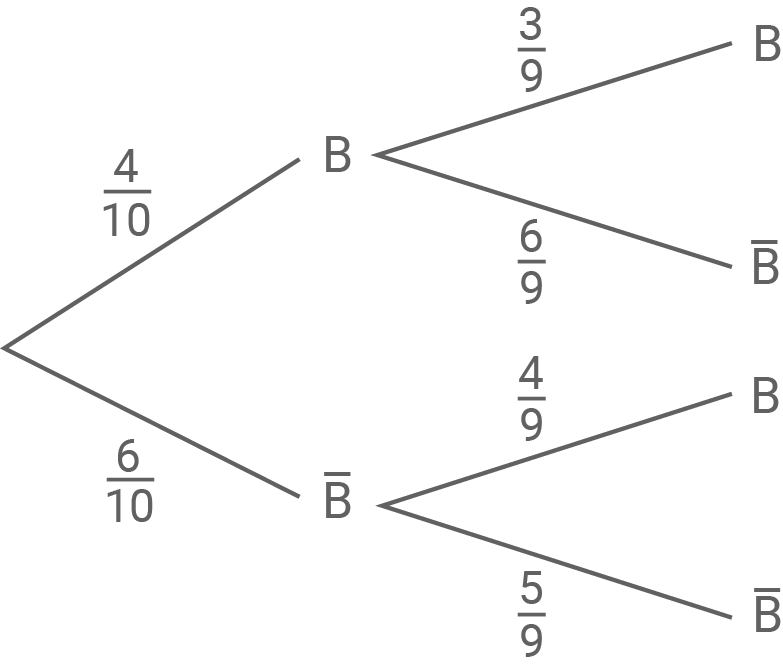
In einem Behälter befinden sich rote, grüne und 4 blaue Kugeln. Insgesamt sind 10 Kugeln im Behälter.

Es werden zwei Kugeln nacheinander ohne Zurücklegen zufällig gezogen.

9.1

Zeige, dass die Wahrscheinlichkeit für das Ziehen zweier blauer Kugeln $\dfrac{2}{15}$ beträgt.

(2 BE)

9.2

Die Wahrscheinlichkeit, dass unter den zwei gezogenen Kugeln genau eine grüne Kugel ist, beträgt $\dfrac{7}{15}.$

Bestimme die Anzahl der grünen Kugeln im Behälter.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1. Schritt: Flächeninhalt $\boldsymbol{T_2}$ berechnen

Der Punkt $B$ besitzt aufgrund der Achsenparallelität des Rechtecks die Koordinaten $B(4\mid 0).$

Für den Flächeninhalt $T_2$ gilt also:

$\begin{array}[t]{rll} T_2&=& \displaystyle\int_{0}^{4}f_a(x)\;\mathrm dx&\\[5pt] &=& \left[\dfrac{1}{3}\cdot a\cdot x^3\right]_0^4&\\[5pt] &=& \dfrac{1}{3}\cdot a\cdot 64-\dfrac{1}{3}\cdot a\cdot 0&\\[5pt] &=& \dfrac{1}{3}\cdot 64a \;[\text{FE}] \end{array}$

2. Schritt: Flächeninhalt $\boldsymbol{A_R}$ des Rechtecks berechnen

Durch Subtrahieren des Flächeninhalts $T_2$ vom Flächeninhalt des Rechtecks ergibt sich der Flächeninhalt $T_1.$

Das Rechteck $ABC_aD_a$ besitzt die Breite $|\overline{AB}|=4$ und die Höhe $|\overline{BC}|=f_a(4).$ Diese ergibt sich mit:

$f_a(4)=a\cdot 4^2=16a\;[\text{LE}]$

Das Rechteck besitzt somit den Flächeninhalt $A_{R}=4\cdot 16a=64a \;[\text{FE}].$

3. Schritt: Flächeninhalt $\boldsymbol{T_1}$ berechnen

$\begin{array}[t]{rll} T_1&=& A_R -T_2 & \\[5pt] &=& 64a-\dfrac{1}{3}\cdot 64a& \\[5pt] &=& \dfrac{2}{3}\cdot 64a \end{array}$

4. Schritt: Verhältnis untersuchen

Für das Verhältnis von $T_1$ und $T_2$ gilt:

$\dfrac{T_1}{T_2}=\dfrac{\frac{2}{3}\cdot 64a}{\frac{1}{3}\cdot 64a}=\dfrac{\frac{2}{3}}{\frac{1}{3}}=\dfrac{2}{1}$

Das Verhältnis der Flächeninhalte der beiden Teilflächen ist somit unabhängig von $a.$

8.1

Lage begründen

Die Punkte $A,B$ und $C$ haben alle die $x$ -Koordinate $x=0$ und liegen somit in der $yz$ -Ebene.

Abstand angeben

Die $xy$ -Ebene wird durch $z=0$ definiert. Der Abstand eines Punktes zur $xy$ -Ebene ist folglich der Betrag seiner $z$ -Koordinate. Für den Punkt $C(0\mid 4\mid 3)$ beträgt dieser Abstand daher:

$|z_C|=|3|=3$

8.2

Ein Trapez hat zwei parallele Seiten. Da $A,B$ und $C$ in der $yz$ -Ebene liegen, muss der Punkt $D$ ebenfalls in der $yz$ -Ebene liegen, also muss gelten: $D(0\mid y \mid z)$

Die Strecke $\overline{AB}$ verläuft parallel zur $y$ -Achse. Damit die Strecke $\overline{CD}$ parallel zur Seite $\overline{AB}$ und somit ebenfalls zur $y$ -Achse liegt, müssen $C$ und $D$ die selbe $z$ -Koordinate besitzen. Für $D$ folgt also $D(0\mid y \mid 3).$

Die Höhe des Trapezes ist die Differenz der $z$ -Werte zwischen $A$ und $D$ bzw. $B$ und $C$ und somit $z_D-z_A=3-1=2.$

Für den Flächeninhalt $A$ des Trapezes soll gelten:

$A=7$ und somit $y_D=1$

Rechenweg anzeigen

Das Viereck $ABCD$ ist somit genau dann ein Trapez mit dem Flächeninhalt 7, wenn $D$ die Koordinaten $D(0\mid1\mid 3)$ besitzt.

9.1

$B:$ Ziehen einer blauen Kugel

Blaue Kugel Wahrscheinlichkeit Sachsen Mathe Abi 2024

Es gilt:

$\begin{array}[t]{rll} P(B,B)&=& \dfrac{4}{10}\cdot \dfrac{3}{9}& \\[5pt] &=& \dfrac{2}{5}\cdot \dfrac{1}{3}& \\[5pt] &=& \dfrac{2}{15} \end{array}$

9.2

$G:$ Ziehen einer grünen Kugel

$R:$ Ziehen einer roten Kugel

$g,r$ und $b$ bezeichnen jeweils die Anzahl der grünen, roten bzw. blauen Kugeln im Behälter.

Da es insgesamt 10 Kugeln gibt und davon 4 blaue, gilt für die Anzahl der roten Kugeln:

$\begin{array}[t]{rll} r&=& 10-g-b& \\[5pt] &=& 10-g-4& \\[5pt] &=& 6-g \end{array}$

Für die Wahrscheinlichkeit $P_G,$ dass unter den zwei gezogenen Kugeln genau eine grüne Kugel ist, folgt somit:

$P(G)= \dfrac{10g-g^2}{45}$

Rechenweg anzeigen

Es soll gelten:

$\begin{array}[t]{rll} P_G&=& \dfrac{7}{15}&\\[5pt] \dfrac{10g-g^2}{45}&=& \dfrac{21}{45}&\quad \scriptsize \mid\; \cdot 45\\[5pt] 10g-g^2&=& 21&\quad \scriptsize \mid\; +g^2 \quad \scriptsize \mid\; -10g \\[5pt] 0&=& g^2-10g+21 \end{array}$

Mit der pq-Formel ergibt sich:

$\begin{array}[t]{rll} g_{1;2}&=& -\dfrac{(-10)}{2} \pm \sqrt{\left(\dfrac{(-10)}{2}\right)^2-21} & \\[5pt] g_{1;2}&=& 5\pm\sqrt{25-21}& \\[5pt] g_{1;2}&=& 5\pm 2& \\[5pt] g_1&=& 3& \\[5pt] g_2&=& 7 \end{array}$

Da es insgesamt 10 Kugeln gibt und davon 4 blau sind, kann die Anzahl der grünen Kugeln maximal 6 betragen.

Die Anzahl der grünen Kugeln im Behälter beträgt somit 3.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?